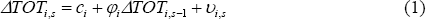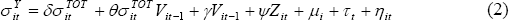RDP 2009-05: Macroeconomic Volatility and Terms of Trade Shocks 3. Data and Methodology
October 2009
We use a sample of 71 countries/economies with data for the period 1971 to 2005. As is common in the literature, we transform our data into five-year averages, with the first period including the years 1971 to 1975 and the final period including the years 2001 to 2005. Detailed data descriptions and sources are provided in Appendix A and a list of countries is provided in Appendix B.
In order to examine the effect of terms of trade shocks, it is first necessary to define these shocks. While a common approach in the literature is to use the standard deviation of terms of trade growth to measure terms of trade volatility (Beck et al 2006), some terms of trade movements are likely to be predictable. If so, changes in the terms of trade will be imperfect proxies for terms of trade shocks. In particular, to the extent that firms and households act in a forward-looking manner, failing to take account of predictable terms of trade movements could bias our estimates of the effects of terms of trade volatility towards zero.
To control for anticipated terms of trade movements, we follow Kent and Cashin (2003), and estimate equations of the form:
where ΔTOTi,s is the growth rate of the terms of trade
in country i at time s and ci is a constant
term for country
i.[6]
It is important to emphasise that we allow the slope coefficient in Equation (1),
øi, to vary across countries. This allows
the persistence of terms of trade movements to differ across economies. The
residual from Equation (1), νi,s, represents the terms
of trade shock to country i at time s. Our measure of the
volatility of terms of trade shocks is the log of the standard deviation of
νi,s
over each five-year block (henceforth 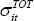 ), where t
identifies the date of the five-year block.
), where t
identifies the date of the five-year block.
The dependent variables in our regressions are the volatilities of output growth, CPI inflation and the expenditure components of output – household consumption, gross fixed capital formation, public consumption expenditure, exports and imports. All output variables are measured in real per capita terms. As was the case for the terms of trade, we first extract the unexpected component of each variable by regressing its annual change on a constant and a single lag, and then calculate volatility as the log of the standard deviation of the residuals from this equation within each five-year block, t.
We estimate fixed-effects panel regressions to examine the effect of the volatility of terms of trade shocks on the volatility of output and inflation. Each regression takes the form:
where: 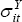 is the log of the standard deviation of the dependent variable of interest for country
i,
is the log of the standard deviation of the dependent variable of interest for country
i, 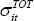 is the log of the standard deviation of
the terms of trade shock, Vit
is a vector of structural variables and Zit is a vector
of control variables. To capture the likely lagged effect of structural change
and to ensure that the structural indicators are exogenous, we follow Kent
et al (2005) and include the structural variables in our
regressions with a lag. That is, we match the volatility of annual GDP over
a given five-year block at time t, with the value of the structural
indicator that applies in the year just prior to this (for example, output
volatility over the five years ending 1975 is matched with the level of financial
market development in 1970). We also include country-specific fixed effects
(μi) to control for time-invariant factors that affect
is the log of the standard deviation of
the terms of trade shock, Vit
is a vector of structural variables and Zit is a vector
of control variables. To capture the likely lagged effect of structural change
and to ensure that the structural indicators are exogenous, we follow Kent
et al (2005) and include the structural variables in our
regressions with a lag. That is, we match the volatility of annual GDP over
a given five-year block at time t, with the value of the structural
indicator that applies in the year just prior to this (for example, output
volatility over the five years ending 1975 is matched with the level of financial
market development in 1970). We also include country-specific fixed effects
(μi) to control for time-invariant factors that affect
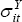 ,
including country size, as well as time-fixed effects (τt)
to control for common shocks.
,
including country size, as well as time-fixed effects (τt)
to control for common shocks.
This empirical framework allows us to estimate how different structural characteristics
affect the propagation of terms of trade shocks 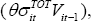 as well as to control for the magnitude of terms of trade shocks
as well as to control for the magnitude of terms of trade shocks 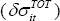 explicitly. The estimated
coefficient
explicitly. The estimated
coefficient 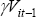 captures how the various structural characteristics
condition the responsiveness of the economy to all other shocks, as well as
the size of these shocks.
captures how the various structural characteristics
condition the responsiveness of the economy to all other shocks, as well as
the size of these shocks.
We interact the terms of trade with several variables intended to represent policy frameworks and other structural features of the economy relevant to the propagation of terms of trade shocks. Our measure of exchange rate flexibility is a dummy variable that takes a value of one if an economy has a floating or managed floating exchange rate according to the de facto exchange rate classification system of Reinhart and Rogoff (2004), and zero otherwise.[7] We prefer this measure of exchange rate flexibility to alternative de jure classification schemes (as used in Ghosh et al 1997) as it is actual exchange rate flexibility, rather than the formal exchange rate regime, that is likely to influence an economy's adjustment to terms of trade shocks.[8]
To account for the role of monetary policy as a determinant of macroeconomic volatility, we construct a dummy variable intended to capture the extent to which the monetary policy framework focuses on low inflation, hereafter referred to simply as ‘strict’ monetary policy. Similar to Kent et al (2005), we assume that Germany, Japan and Switzerland had strict monetary regimes throughout the sample period. Monetary policy in the United States is deemed to have had strict monetary policy from 1981 – corresponding to the first complete five-year block of the Volcker chairmanship – while monetary policy in other European countries is assumed to have become strict when they joined the euro area. Finally, an economy's monetary policy is assumed to have become strict in the year in which it adopted a formal inflation target (IMF 2006).
It is worth noting that this variable could well underestimate the number of ‘strict’ monetary policy observations in our sample. In particular, it omits economies that import effective monetary policy by pegging their nominal exchange rate to the currency of an economy whose central bank is strict on inflation. We excluded this type of monetary policy regime for two reasons. First, it is difficult to differentiate between economies that adopt an inflexible nominal exchange rate regime to stabilise inflation from those that do so for other reasons, including strategic trade policy. Second, the benefits of a pegged exchange rate for macroeconomic stability are better captured by our exchange rate dummy variable. Excluding countries which adopt a pegged exchange rate in order to help stabilise inflation (and output) will tend to bias the estimated coefficients on our strict monetary policy variable, and its interaction terms, towards zero.
We measure financial development in terms of the level of domestic credit provided to the private sector (as a share of GDP). This is a widely used measure of financial development (Levine, Loayza and Beck 2000; Beck et al 2006), which indicates the extent to which a country's financial system channels funds from savers to private sector investors. We interpret higher levels of private credit as an indication of a more developed financial system.
We consider two measures of labour market flexibility. The first is constructed using the index of labour market regulations component of the Economic Freedom of the World report, published by the Fraser Institute (Gwartney and Lawson 2008).[9] This index takes a value between one and ten, with a higher number indicating a less regulated labour market. The index value depends on a number of factors, including: the value of a country's mandated minimum wage relative to average value added per worker; regulations concerning the hiring and firing of workers; and the degree of wage decentralisation. For estimation purposes, we use this index to construct three dummy variables: low labour market flexibility, medium labour market flexibility and high labour market flexibility, which correspond to the bottom, middle and top thirds of the distribution respectively. We adopt this approach for both ease of interpretation and to allow for the possible hump-shaped relationship between labour market flexibility and macroeconomic outcomes (Calmfors and Driffill 1988).
While this measure of labour market flexibility is available for a large number of countries and the relative values of the index between countries and over time appear to correspond broadly with known periods of labour market deregulation, it has limitations. For instance, it is only able to capture a limited set of factors that determine how the labour market operates and tends to rely heavily on subjective interpretations of the legal framework. With this in mind, we also follow Andrews and Kohler (2005) and include union density to proxy the degree of labour market flexibility, although this reduces the number of countries in our sample by roughly one-fifth to 56 countries.
For this empirical framework to reliably identify the macroeconomic effects of terms of trade shocks, we need to assume that terms of trade shocks are exogenous with respect to output volatility. This is potentially problematic for large economies or countries that have a sizeable market share in a particular good (Broda 2004; Edwards and Levy Yeyati 2005).[10] Given the lack of suitable instruments for the terms of trade, the standard approach in the literature has been to exclude those economies from the analysis where the exogeneity assumption is likely to be problematic. Using a sample of countries similar to ours, Edwards and Levy Yeyati (2005) found their results to be robust to such an approach, leading them to conclude that their results are unlikely to be driven by terms of trade endogeneity. In Section 5 we show that our results are also broadly robust to the exclusion of specific groups of economies where the exogeneity assumption is likely to be more of a concern.
We also include a number of control variables in our regressions. Consistent with the related literature, all regressions contain a measure of openness to international trade (proxied by the ratio of exports plus imports to GDP). The inflation volatility regressions also include the log of the average annual rate of inflation in the five years prior to the start of each window as well as a dummy variable that takes a value of one if an economy experiences a currency crisis during a five-year window.[11] All regressions include time-fixed effects to control for the general decline in macroeconomic volatility through our sample. Throughout the paper, we calculate robust standard errors that allow for heteroskedasticity of unknown form.
Table 2 shows the key summary statistics for our variables. As to be expected, the shocks to household consumption are considerably less volatile than the shocks to other expenditure components. While the estimated shocks contained in Table 2 also imply that consumption is more volatile than output, this result is driven by the numerous commodity producers in our sample.[12] Table C1 shows correlations across these different variables, while further information on the construction of our variables is presented in Appendix A.
| Mean | Standard deviation | Min | Max | |
|---|---|---|---|---|
| Dependent variables(a) | ||||
| SD real GDP shocks | 2.68 | 2.01 | 0.36 | 12.19 |
| SD consumption shocks | 3.70 | 3.40 | 0.20 | 22.72 |
| SD investment shocks | 9.46 | 7.28 | 1.23 | 46.97 |
| SD government consumption shocks | 4.59 | 4.67 | 0.21 | 32.64 |
| SD export shocks | 7.50 | 5.33 | 0.68 | 45.52 |
| SD import shocks | 9.56 | 6.07 | 1.03 | 35.91 |
| SD inflation shocks | 31.42 | 300 | 0.19 | 5087 |
| Independent variables | ||||
| SD terms of trade shocks(a) | 8.25 | 7.45 | 0.55 | 42.48 |
| Private credit (share of GDP)(b) | 49 | 38 | 2 | 222 |
| Floating exchange rate dummy(c) | 0.30 | 0.46 | 0.00 | 1.00 |
| Strict monetary policy dummy(d) | 0.13 | 0.33 | 0.00 | 1.00 |
| Openness (total trade as a share of GDP)(e) | 63 | 36 | 8 | 291 |
| Notes: All descriptive statistics are based on a sample of 71 countries
and 411 observations. (a) Standard deviation (SD) of the annual shocks (that is, the residual from Equation (1), estimated over a five-year window. Note that the regression analysis later in the paper is based on the natural log of the standard deviation of these shocks over the same five-year window. (b) Total private credit as a per cent of nominal GDP; annual average observed at five-year intervals. (c) Dummy variable that takes a value of one if an economy has a floating or managed floating exchange rate according to the de facto exchange rate classification system of Reinhart and Rogoff (2004), and zero otherwise. (d) Dummy variable that takes a value of one if an economy's monetary authorities are deemed to have been strict on inflation, and zero otherwise. See Section 3 for more detail. (e) The value of total trade as a per cent to nominal GDP; annual average observed at five-year intervals. |
||||
Footnotes
As is standard, our measure of the terms of trade is the ratio of a price index of an economy's exports of goods and services to a price index of its imports of goods and services. [6]
The Reinhart and Rogoff classification system orders exchange rate regimes into four categories from the most rigid to the most flexible: fixed, pegged, managed float and float. [7]
We also considered the alternative Levy Yeyati and Sturzenegger (2002) de facto classification system. However, we preferred the Reinhart and Rogoff classification because it is available for a much larger number of countries, and over a longer sample. [8]
Kent et al (2005) also used the number of days lost in labour disputes as a proxy for the extent of labour market regulation. While this measure can capture labour market outcomes more directly, and captures a broader range of factors that determine how the labour market operates than the data on the labour market regulations we use, it is not widely available for the larger number of countries in our sample. [9]
Even for small economies, such as Australia, long-run terms of trade movements could be endogenous to the extent that the composition of imports and exports changes over time (Gillitzer and Kearns 2005). However, over any given five-year window, exogeneity is still likely to be a reasonable assumption. [10]
The currency crisis dummy takes a value of one if a country experienced a free-falling exchange rate regime, as defined by Reinhart and Rogoff (2004), at any time during a five-year window. These episodes tend to be associated with the abandonment of fixed exchange rate regimes. [11]
In the G7 economies, for example, the volatility of the shocks to consumption are lower than the volatility of the shocks to output. [12]