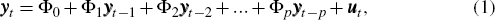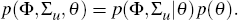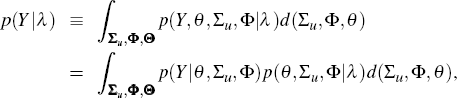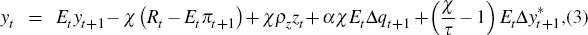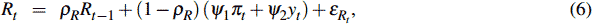RDP 2008-04: A Small BVAR-DSGE Model for Forecasting the Australian Economy 2. Methodology – Estimation

This section provides a brief overview of the methodology used to estimate the BVAR-DSGE; further details can be found in Del Negro and Schorfheide (2004), which we follow closely.

2.1 Some Notation

Let the parameters of the DSGE model, which we will describe further below, be denoted by the vector θ. Let the column vector of n observable variables be y_t, which are also assumed to be the variables in the VAR. That is,

where: Φ₀ is a vector of constants; Φ_1..p are matrices of VAR parameters; and u_t ~ N(0,Σ_u).^[4] This can be written more compactly as Y = XΦ + U, where: Y and U are matrices with rows 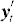and respectively; X has rows 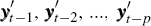and 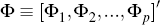. It is noteworthy that the number of parameters in the DSGE model is much smaller than that in the VAR, hence the greater ability of the VAR to fit the data.

2.2 Priors for the VAR Parameters

In this paper we want to use a DSGE model to provide information about the parameters of the VAR. Intuitively, one way of doing this is to simulate data from the DSGE and to combine it with the actual data when estimating the VAR. The relative share of simulated observations compared to the actual data, λ, governs the relative weight placed on the prior information. However, as the DSGE model specifies the stochastic process for y_t, rather than simulating data we can instead use the solution to the log-linearised DSGE model to analytically compute the population moments of y_t. The role of λ therefore is to scale these moments so as to be equivalent in magnitude to the (non-standardised) sample moments that would have been obtained through simulation. It is then possible to formulate the prior for the VAR parameters p(Φ,Σ_u|θ) (for given DSGE model parameters θ), in Inverted-Wishart (IW)-Normal (N) form, that is, Σ_u|θ ~ IW and Φ|Σ_u,θ ~ N. The parameters of these prior densities are functions of the population moments calculated from the DSGE model.^[5]

2.3 Priors for the DSGE Parameters

We also have prior beliefs about the parameters of the DSGE model, p(θ). The joint prior density of both sets of parameters is:

2.4 The VAR Posterior

The posterior distribution of the VAR parameters Φ and Σ_u, p(Φ,Σ_u|Y,θ), from which we will draw parameters when forecasting, is obtained by combining the prior with information from the data, namely the likelihood function. The likelihood, reflecting the distribution of the innovations (u_t), is multivariate normal, which is particularly useful as the priors described above for the VAR parameters are of Inverted-Wishart-Normal form, and these conjugate. Consequently, the posterior follows the same class of distributions as the prior, that is, Σ_u|θ,Y ~ IW and Φ|Σ_u,θ,Y ~ N.^[6] Finally, we can simulate the posterior for the VAR parameters by first drawing a θ from the posterior of the DSGE parameters and then sampling from these distributions.

2.5 Choosing the Lag Length and the Weight on the Prior, λ

The VAR posterior is conditional on a choice of λ, the relative weight given to the DSGE prior. Let the set of possible λ be Λ, where Λ ≡ {λ₁,..., λ_i,..., λ_q}, and for all i, λ_i > 0. The approach suggested by Del Negro and Schorfheide (2004) is to compare the model evaluated at each 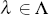, using the metric of the marginal data density, p(Y|λ).^[7] This is somewhat akin to an information criterion, and can be obtained by integrating out the parameters of the joint density of the data and the parameters

where Σ_u, Φ and Θ are the parameter spaces (that is, the sets of possible parameter values) for Σ_u, Φ and θ. As pointed out by Christiano (2007), the integration involved in calculating the marginal data density is computationally intensive. However, recall that the joint prior density of the VAR and DSGE parameters, p(Φ,Σ_u,θ|λ), equals p(Φ,Σ_u,|θ,λ)p(θ), and the prior of the VAR parameters given θ is of Inverted-Wishart-Normal form. The latter enables the integrals with respect to the VAR parameters to be calculated analytically, leaving only the integral with respect to θ to be calculated in order to approximate p(Y|λ).^[8] An ‘optimal’ λ, 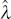, could then be chosen to maximise p(Y|λ), that is,

As noted by Del Negro and Schorfheide (2004), we could also use the marginal data density to pick the lag length of the VAR, p.

However, as the primary purpose of this model is forecasting, an alternative approach is to choose λ and the lag length with respect to the out-of-sample forecasting performance, which we describe in Section 4.2.

2.6 The DSGE Model

The DSGE model we use as the source of the prior information is a variant of the model by Lubik and Schorfheide (2007), which itself is a simplified version of Galí and Monacelli (2005). The Lubik and Schorfheide (2007) model has previously been used in the estimation of a BVAR-DSGE for New Zealand by Lees, Matheson and Smith (2007), and while not without criticism (for example, Fukač and Pagan forthcoming), as argued by Lees et al (2007) it probably represents the smallest possible DSGE model for a small open economy. It is worth noting that our model lacks many of the traditional features used in DSGE models to enhance their fit, such as habit persistence in consumption or indexation in price setting. The model has microeconomic foundations; however, as they are not our focus we only provide a brief overview of the key final log-linearised equations of the model which we will use.^[9]

where: 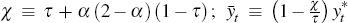; Δ is the first difference operator; and E_t is the expectation operator conditional on period t information. An appealing feature of the model is that world (and hence domestic) technology, A_t, is assumed to follow a non-stationary process. A consequence of this is that some of the real variables (such as output) are normalised by technology before the log-linearisation. All variables are expressed as (approximate) per cent deviations from their steady-state values. Technology is assumed to grow at the rate z_t, that is, z_t ≡ lnA_t−1, which follows an AR(1) process, z_t = p_zz_t−1 + ε_zt. Output is denoted by Y_t, R_t denotes the quarterly gross interest rate, q_t is the terms of trade, π_t is inflation, e_t is the nominal exchange rate (defined so that a fall is an appreciation), ȳ_t is the level of potential output (that is, the level of output consistent with flexible prices), and variables with a superscript * are the equivalent world variables.

Equation (3) is the IS curve, which is derived from the consumers' Euler equation; the parameters α, β and τ are the import share of domestic consumption, the discount factor and the intertemporal elasticity of substitution, respectively. Output depends on the expectations of future output both at home and abroad, the real interest rate, expected changes in the terms of trade and technology growth.

Equation (4) is the open-economy Phillips curve, which can be derived from assuming a continuum of monopolistic firms which only use labour in production and set prices à la Calvo. Movements in the output gap affect inflation as they are associated with changes in real marginal costs; the parameter κ affects the slope of the Phillips curve and is a function of other deeper parameters, but here is taken to be structural. Changes in the terms of trade enter the Phillips curve reflecting the fact that some consumer goods are imported and also reflecting the assumption of relative purchasing power parity (PPP), as per Equation (5).

Monetary policy, as specified in Equation (6), is assumed to partially adjust the nominal rate (at rate 1 — p_R) to the level suggested by a Taylor rule, following Clarida, Galí and Gertler (2000). The weights on inflation and output in the Taylor rule are given by ψ₁ and ψ₂.^[10]

The change in the terms of trade in this model is assumed to follow an AR(1) process, as are world output 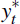and inflation 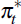, with autoregression coefficients p_Δq, p_y* and p_π*, respectively. The structural shocks are denoted by ε_variablet.

Footnotes

As we de-mean the data, we suppress Φ₀ in what follows. [4]

See Equations (24) and (25) in Del Negro and Schorfheide (2004). [5]

Once again we have suppressed the parameters of the posterior distributions – see Equations (30) and (31) in Del Negro and Schorfheide (2004). [6]

The notation of the marginal data density follows Del Negro et al (2007). Also, previously we suppressed the fact that many of the densities (for example, the joint prior density for the VAR and DSGE parameters) are conditional on λ. [7]

This is done using Geweke's harmonic mean estimator (Geweke 1999); see also An and Schorfheide (2007). [8]

See Appendix A and the above references (particularly Galí and Monacelli 2005) for the derivations. Lubik and Schorfheide (2005) is also a useful reference. [9]

We deviate from Lubik and Schorfheide (2007) and assume that the Taylor rule does not include the exchange rate. [10]