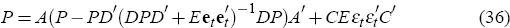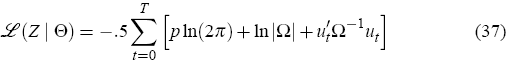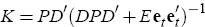RDP 2007-01: A Structural Model of Australia as a Small Open Economy 3. Estimation Strategy
February 2007
- Download the Paper 256KB
The parameters of the model are estimated using Bayesian methods that combine prior
information and information that can be extracted from aggregate data series.
An and Schorfheide (forthcoming) provide an overview of the methodology. Conceptually,
the estimation works in the following way. Denote the vector of parameters
to be estimated Θ = {γ, η,φ,...} and the log of the prior probability of
observing a given vector of parameters 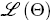 . The function
. The function 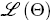 summarises what is known about the parameters prior to estimation. The log likelihood
of observing the data set Z for a given parameter vector Θ is denoted
summarises what is known about the parameters prior to estimation. The log likelihood
of observing the data set Z for a given parameter vector Θ is denoted
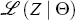 .
The posterior estimate
.
The posterior estimate 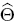 of the parameter vector is then found by
combining the prior information with the information in the estimation sample.
In practice, this is done by numerically maximising the sum of the two over
Θ, so that
of the parameter vector is then found by
combining the prior information with the information in the estimation sample.
In practice, this is done by numerically maximising the sum of the two over
Θ, so that 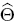 = argmax
= argmax 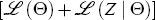 .
.
The first step of the estimation process is to specify the prior probability over the parameters Θ. Prior information can take different forms. For instance, for some parameters, economic theory determines the sign. For other parameters we may have independent survey data, as is the case for the frequency of price changes, for example.[7] Priors can also be based on similar studies where data for other countries were used. The restrictions implied by the theoretical model means that prior information about a particular parameter can also be useful for identifying other parameters more sharply. For instance, it is typically difficult to separately identify the degree of price stickiness Θ and the curvature of the disutility of supplying labour φ just by using information from aggregate time series. However, a combination of the two variables may have strong implications for the likelihood function (that is, there may be a ‘ridge’ in the likelihood surface). Survey evidence suggests that the average frequency of price changes is somewhere between 5 and 13 months. By choosing a prior probability for the range of the stickiness parameter Θ that reflects this information, we may also identify φ more sharply.
Unfortunately, we do not have independent information about all of the parameters of the model. A cautious strategy when hard priors are difficult to find is to use diffuse priors, that is, to use prior distributions with wide dispersions. If the data are informative, the dispersion of the posterior should be smaller than that of the prior. However, Fukac et al (2006) point out that using informative priors, even with wide dispersions, can affect the posteriors in non-obvious ways.
Arguably, hard prior information exists for the discount factor β, the steady state share of imports/exports in GDP α and the average duration of good prices Θd and Θm. The first two can be deduced from the average real interest rate and the average share of imports and exports of GDP and are calibrated as {β, α} = {0.99,0.18}. Calibration can be viewed as a very tight prior. The price stickiness parameters Θd and Θm are assigned priors that are centered around the mean duration found in European data (see Alvarez et al 2005).
The prior distributions of the variances of the exogenous shocks are truncated uniform over the interval [0,∞). It is common to use more restrictive priors for the exogenous shocks, as for example in Smets and Wouters (2003), Lubik and Schorfheide (forthcoming), Justiniano and Preston (2005) and Kam, Lees and Liu (2006), but since most shocks are defined by the particular model used, it is unclear what the source of the prior information would be.
The priors of the variances of the measurement error parameters are uniform distributions
on the interval 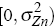 where
where 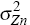 is the variance of the corresponding time series. Economic theory dictates the domains
of the rest of the priors, but we have little information about their modes
and dispersions. These priors are therefore assigned wide dispersions. Information
about the prior distributions for the individual parameters are given in Table
1.
is the variance of the corresponding time series. Economic theory dictates the domains
of the rest of the priors, but we have little information about their modes
and dispersions. These priors are therefore assigned wide dispersions. Information
about the prior distributions for the individual parameters are given in Table
1.
| Parameter | Distribution | Prior | Posterior | |||
|---|---|---|---|---|---|---|
| Mode | Standard error | Mode | Standard error | |||
| Households and firms | ||||||
| γ | normal | 3 | 0.44 | 3.37 | 0.36 | |
| η | normal | 2 | 0.66 | 1.20 | 0.15 | |
| φ | normal | 2 | 0.44 | 1.89 | 0.43 | |
| ω | beta | 0.3 | 0.10 | 0.73 | 0.06 | |
| δ | normal | 1 | 0.10 | 0.93 | 0.10 | |
| δx | normal | 1 | 0.10 | 0.02 | 0.01 | |
| θ | beta | 0.75 | 0.04 | 0.73 | 0.04 | |
| θm | beta | 0.75 | 0.04 | 0.90 | 0.02 | |
| Ψ | normal | 0.01 | 0.02 | 0.10 | 0.02 | |
| Taylor rule | ||||||
| ϕy | normal | 0.5 | 0.25 | 0.02 | 0.01 | |
| ϕπ | normal | 1.5 | 0.29 | 0.19 | 0.04 | |
| ϕi | beta | 0.5 | 0.25 | 0.87 | 0.03 | |
| Exogenous persistence | ||||||
| ρa | beta | 0.5 | 0.28 | 0.65 | 0.07 | |
| ρs | beta | 0.5 | 0.28 | 0.07 | 0.01 | |
| ρpx | beta | 0.5 | 0.28 | 0.87 | 0.06 | |
| ρx | beta | 0.5 | 0.28 | 0.89 | 0.06 | |
| ρm | beta | 0.5 | 0.28 | 0.71 | 0.13 | |
| Exogenous shock variances | ||||||
 |
uniform | [0,∞) | 4.66 × 10−5 | 1.59 × 10−5 | ||
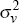 |
uniform | [0,∞) | 4.65 × 10−2 | 5.68 × 10−3 | ||
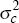 |
uniform | [0,∞) | 2.32 × 10−5 | 7.03 × 10−6 | ||
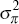 |
uniform | [0,∞) | 6.79 × 10−6 | 2.47 × 10−6 | ||
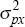 |
uniform | [0,∞) | 5.32 × 10−5 | 1.74 × 10−5 | ||
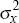 |
uniform | [0,∞) | 7.63 × 10−4 | 6.38 × 10−4 | ||
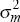 |
uniform | [0,∞) | 1.34 × 10−5 | 4.44 × 10−6 | ||
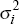 |
uniform | [0,∞) | 7.20 × 10−7 | 1.85 × 10−7 | ||
3.1 Mapping the Model into Observable Time Series
The model of Section 2 is solved by first taking linear approximations of the structural equations around the steady state and then finding the rational expectations equilibrium law of motion. The linearised equations are listed in the Appendix and the Söderlind (1999) algorithm was used to solve the model. The solution can be written in VAR(l) form
where Xt is a vector containing the variables of the model, and the coefficient matrices A and C are functions of the structural parameters Θ. Equation (33) is called the transition equation. The next step is to decide which (combinations) of the variables in Xt are observable. The mapping from the transition equation to observable time series is determined by the measurement equation
The selector matrix D maps the theoretical variables in the state vector Xt into a vector of observable variables Zt. The term et is a vector of measurement errors. For theoretical variables that have clear counterparts in observable time series, the measurement errors capture noise in the data-collecting process. The measurement errors may also capture discrepancies between the theoretical concepts of the model and observable time series. For instance, GDP, non-farm GDP and market sector GDP all measure output, but none of these measures correspond exactly to the model's variable Yt. The measure of total GDP includes farm output, which varies due to factors other than technology and labour inputs, most notably the weather. One may therefore want to exclude farm products. But in the model, more abundant farm goods will lead to higher overall consumption and lower marginal utility, and perhaps also higher exports, so excluding it altogether is also not appropriate. Total GDP also includes government expenditure which is not determined by the utility maximising agents of the model, but it will affect the aggregate demand for labour and therefore market wages. The state space system, that is, the transition Equation (33) and the measurement Equation (34), is quite flexible and can incorporate all three measures of GDP, allowing the data to determine how well each of them corresponds to the model's concept of output. This multiple indicator approach was proposed by Boivin and Giannoni (2005) who argue that not only does this allow us to be agnostic about which data to use, but by using a larger information set it may also improve estimation precision.
Some, but not all, of the observable time series are assumed to contain measurement errors, and the magnitude of these are estimated together with the rest of the parameters. Counting both measurement errors and the exogenous shocks, the total number of shocks in the model are more than is necessary to avoid stochastic singularity. That is, the total number of shocks are larger than the total number of observable variables in Zt. It is reasonable to ask whether all of the shocks can be identified, and the answer is that it depends on the actual data-generating process. The measurement errors are white noise processes specific to the relevant time series that are uncorrelated with other indicators as well as with their own leads and lags. To the extent that the cross-equation and dynamic implications that distinguish the structural shocks from the measurement errors of the model are also present as observable correlations in the time series, it will be possible to identify the structural shocks and the measurement errors separately. Incorrectly excluding the possibility of measurement errors may bias the estimates of the parameters governing both the persistence and variances of the structural shocks. Also, by estimating the magnitude of the measurement errors we can get an idea of how well different data series match the corresponding model concept.
3.2 Computing the Likelihood
The linearised model (33) and the measurement Equation (34) can be used to compute the covariance matrix of the theoretical one-step-ahead forecast errors implied by a given parameterisation of the model. That is, without looking at any data, we can compute what the covariance of our errors would be if the model was the true data-generating process and we used the model to forecast the observable variables. This measure, denoted Ω, is a function of both the assumed functional forms and the parameters and is given by
where P is the covariance matrix of the one-period-ahead forecast errors of the state
The covariance of the theoretical forecast errors Ω is used to evaluate the likelihood of observing the time series in the sample, given a particular parameterisation of the model. Formally, the log likelihood of observing Z given the parameter vector Θ is
where p × T are the dimensions of the observable time series Z and ut is a vector of the actual one-step-ahead forecast errors from predicting the variables in the sample Z using the model parameterised by Θ. The actual (sample) one-step-ahead forecast errors can be computed from the innovation representation
where K is the Kalman gain
The method is described in detail in Hansen and Sargent (2005).
To help understand the log likelihood function intuitively, consider the case of
only one observable variable so that both Ω and ut are scalars. The last term in the log likelihood function
(37) can then be written as 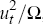 , so for a given squared error
, so for a given squared error 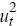 the log likelihood
increases in the variance of the model's forecast error variance. This
term will thus make us choose parameters in θ that make the
forecast errors of the model large since a given error is more likely to have
come from a parameterisation that predicts large forecast errors. The determinant
term 1n|Ω| (the determinant of a scalar is simply the scalar itself)
counters this effect, and to maximise the complete likelihood function we need
to find the parameter vector Θ that yields the optimal trade-off between
choosing a model that can explain our actual forecast errors, ut,
while not making the implied theoretical forecast errors too large.
the log likelihood
increases in the variance of the model's forecast error variance. This
term will thus make us choose parameters in θ that make the
forecast errors of the model large since a given error is more likely to have
come from a parameterisation that predicts large forecast errors. The determinant
term 1n|Ω| (the determinant of a scalar is simply the scalar itself)
counters this effect, and to maximise the complete likelihood function we need
to find the parameter vector Θ that yields the optimal trade-off between
choosing a model that can explain our actual forecast errors, ut,
while not making the implied theoretical forecast errors too large.
Another way to understand the likelihood function is to recognise that there are
(roughly speaking) two sources contributing to the forecast errors ut, namely shocks and incorrect parameters. The set of
parameters Θ that maximise the log likelihood function (37) are those
that reduce the forecast errors caused by incorrect parameters as much as possible
by matching the theoretical forecast error variance Ω with the sample
forecast error covariance 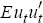 , thereby attributing all remaining forecast
errors to shocks.
, thereby attributing all remaining forecast
errors to shocks.
3.3 The Data
The data sample is from 1991:Q1 to 2006:Q2 where the first eight observations are used as a convergence sample for the Kalman filter. Thirteen time series were used as indicators for the theoretical variables of the model, which is more than that of most other studies estimating structural small open economy models. Lubik and Schorfheide (forthcoming) estimate a small open economy model on data for Canada, the UK, New Zealand and Australia using terms of trade as the only observable variable relating to the open economy dimension of the model. Similarly, in Justiniano and Preston (2005) the real exchange rate between the US and Canada is the only data series relating to the open economy dimension of the model. Neither of these studies use trade volumes to estimate their models. This is also true for Kam et al (2006), though this study uses data on imported goods prices rather than only aggregate CPI inflation.
In this paper, data for the rest of the world are based on trade-weighted G7 output and inflation and an (unweighted) average of US, Japanese and German/euro interest rates. Three domestic indicators that are assumed to correspond exactly to their respective model concepts are the cash rate, the nominal exchange rate, and trimmed mean quarterly CPI inflation. The rest of the domestic indicators are assumed to contain measurement errors. These are GDP, non-farm GDP, market sector GDP, exports as a share of GDP, the terms of trade (defined as the price of exports over the price of imports) and labour productivity. All real variables are linearly detrended and inflation and interest rates were demeaned. The correspondence between the data series and the model concepts are described in Table 2.
| Data | Model | Σee/Σzz |
|---|---|---|
| Interest rate | it | – |
| Nominal exchange rate change | Δst | – |
| CPI trimmed mean inflation | πt | – |
| Real GDP | yt | 0.03 |
| Real non-farm GDP | yt | 0.05 |
| Real market sector GDP | yt | 0.15 |
| Export share of GDP | xt−yt | 0.02 |
| Import share of GDP | 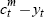 |
0.00 |
| Terms of trade | 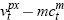 |
0.84 |
| Labour productivity | at | 0.11 |
Footnote
See Bils and Klenow (2004) and Alvarez et al (2005). [7]