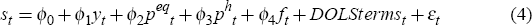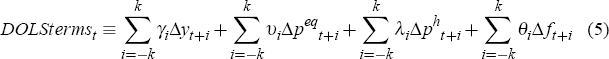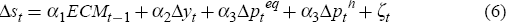RDP 2006-07: Household Saving and Asset Valuations in Selected Industrialised Countries 3. Empirical Assessment
August 2006
- Download the Paper 213KB
This section contains an empirical assessment of Australia, Canada, the UK and the US, where a casual inspection suggests that the co-movement of asset price valuation and private saving has been particularly striking. Indeed, a common pattern appears to be prevalent in these countries, with some similarities in terms of cultural, demographic and institutional characteristics in addition to economic/financial structure and cycles.[12] These countries have had relatively similar experiences over time with regard to asset price developments, propensities to incur debt and access to credit. Moreover, it is likely that households in these countries have relatively similar attitudes vis-à-vis homeownership versus renting along with many similarities in pension schemes.[13]
The empirical results are presented in two parts. First, the results from a single-equation error-correction model (ECM) using quarterly data are presented for these four countries. Supplementing this estimation is an empirical investigation as to whether such relationships have been stable. Second, a panel of these four countries is considered. Appendix A contains further detail regarding the data employed, including sources. Appendix B analyses several possible corrections in the standard statistical measurement of saving. Appendix C provides a discussion of the conceptual link between household saving and wealth.
3.1 Data and Model Specification
An error-correction framework is estimated using the Dynamic Ordinary Least Squares (DOLS) procedure of Stock and Watson (1993), which mitigates the effects of regressor endogeneity on the distribution of the least squares estimator via the inclusion of leads and lags of the first difference of the right-hand-side variables.
The starting point for estimation is Equation (3), augmented with a variable to account for financial change over the sample period as discussed in Section 2. Measures capturing financial deregulation and/or proxies for financial deepening could be, among other things, credit-to-GDP ratios, ratios of monetary aggregates to GDP or interest rate spreads. The ratio of household debt to disposable income is chosen as the proxy for financial liberalisation, given that it should capture effects of financial innovation through their impact on expanding household borrowing.
The specification is as follows, with all variables in logs:[14]
where: st is the level of the real personal saving at time t; yt is the level of real disposable income;[15] peqt is an index for real equity prices; pht is an index for real residential housing prices; ft is the financial liberalisation measure; and
The associated short-term specification of the ECM is:
where ECMt−1 is the lag of the residual from the long-run equilibrium levels Equation (4) estimated above.
Data are quarterly, and the common estimation period starts in 1970 for all countries except Australia, for which data on household debt are only available from 1977 onward.
As outlined in Appendix A, household saving, income and debt data are taken from national sources, while BIS data are used for real price indices for equities and residential housing, proxying for changes in the real value of household wealth. Price indices rather than the real value of wealth are included, reflecting limitations in obtaining a complete set of comparable quarterly data across the countries.[16] All variables are deflated using the price deflator for personal consumption from the national accounts.
3.2 Individual Analysis of Countries
On the basis of Augmented Dickey-Fuller (ADF) tests and taking into consideration possible structural breaks, all variables entering the specification (in levels) are found to be difference stationary, and so are modelled as I(1) stochastic processes within a single cointegrating relation for each country.
From the ECM estimations, reported in Table 1, the following observations can be made:
| US 1970:Q3–2002:Q4 |
Australia 1977:Q2–2002:Q1 |
||||||
|---|---|---|---|---|---|---|---|
| Coefficient estimate | SE |
p-value |
Coefficient estimate | SE |
p-value |
||
| Estimation in log-levels | |||||||
| Disposable income (y) | 1.023 | 0.272 | 0.00 | 1.079 | 0.564 | 0.06 | |
| Equity price index (peq) | −0.596 | 0.080 | 0.00 | −0.236 | 0.164 | 0.15 | |
| House price index (ph) | −1.214 | 0.483 | 0.01 | −0.813 | 0.407 | 0.05 | |
| Debt-income ratio (f) | −0.240 | 0.521 | 0.65 | −1.336 | 0.239 | 0.00 | |
| Estimation in log differences | |||||||
| ECM(−1) | −0.224 | 0.084 | 0.01 | −0.422 | 0.171 | 0.02 | |
| Δy | 8.464 | 1.122 | 0.00 | 12.852 | 1.592 | 0.00 | |
| Δpeq | −0.339 | 0.194 | 0.08 | −0.134 | 0.362 | 0.71 | |
| Δph | −3.955 | 1.282 | 0.00 | −2.266 | 1.178 | 0.06 | |
| Canada 1970:Q3–2002:Q4 |
UK 1970:Q3–2002:Q4 |
||||||
|---|---|---|---|---|---|---|---|
| Coefficient estimate | SE | p-value | Coefficient estimate | SE | p-value | ||
| Estimation in log-levels | |||||||
| Disposable income (y) | 1.674 | 0.123 | 0.000 | 2.027 | 0.214 | 0.00 | |
| Equity price index (peq) | −0.869 | 0.089 | 0.000 | −0.559 | 0.087 | 0.00 | |
| House price index (ph) | 1.029 | 0.207 | 0.000 | −0.985 | 0.205 | 0.00 | |
| Debt-income ratio (f) | −1.886 | 0.173 | 0.000 | 1.514 | 0.238 | 0.03 | |
| Estimation in log differences | |||||||
| ECM(−1) | −0.224 | 0.068 | 0.001 | −0.154 | 0.065 | 0.02 | |
| Δy | 5.374 | 0.565 | 0.000 | 9.549 | 0.750 | 0.00 | |
| Δpeq | −0.173 | 0.113 | 0.127 | −0.165 | 0.142 | 0.25 | |
| Δph | −0.377 | 0.280 | 0.181 | −1.625 | 0.399 | 0.00 | |
| Notes: Dummy variables included in levels equation: US – 2001:Q4, 2002:Q1, 2002:Q4; Australia – 1998:Q2, 1991:Q1, 1999:Q4, 2001:Q2; Canada – 2002:Q2, 2002:Q3, 2002:Q4; UK – 2000:Q1. These are included to mitigate the impact of outliers on the estimation. | |||||||
- the long-run income effect from the cointegration equation indicates that income enters the specification significantly and with the expected positive sign; the estimated long-run elasticity of saving with respect to disposable income is close to one (except for the UK, where it is higher). Such elasticities are associated with an implied long-run marginal propensity to save out of disposable income[17] in the vicinity of 0.07 for Australia and the US and a somewhat higher 0.17 for Canada and the UK.[18] The dynamic response to income is significant, positive, and sizeable, implying considerable adjustment in saving around its long-run equilibrium level in response to changes in income, consistent perhaps with consumption smoothing;
- an examination of the long-run wealth effect indicates that increases in both residential housing prices and equity prices have tended to reduce household saving, except in the case of Canada (where cycles in the housing price index around its trend in the late 1980s and early 1990s may have exerted some influence on the result, mirroring a similar finding in Bertaut 2002). With this one exception, the responsiveness of saving, in absolute value, to equity prices is much lower than it is to house prices.[19] This may indicate the relative ease of extracting capital gains from housing and/or the wider holding of housing assets among the general population (Barrell and Davis 2004). As for wealth effects in the dynamic equation, saving is more responsive in the short-run to changes in house prices relative to equity prices. This may reflect a slower response of saving to equity price movements given a perception on the part of households that house price movements are more permanent than movements in financial assets (Lettau and Ludvigson 2003),[20] along with ease of access to housing equity in these countries and wider homeownership relative to equity holdings;
- the long-run coefficient estimates on the debt-to-income ratio generally suggest a negative impact on saving from financial innovation, or a reduction in saving from an increased ease in borrowing. However, the opposite is true for the UK, suggesting that the development of the financial system may have enhanced opportunities for, and returns to, saving (out of disposable income); and
- the speed of adjustment terms in the dynamic equations indicate that cointegration holds in all cases, and points to a fairly rapid adjustment to long-run equilibrium.
One additional issue which warrants special attention is whether the relationship between saving and its determinants has changed through time.[21]
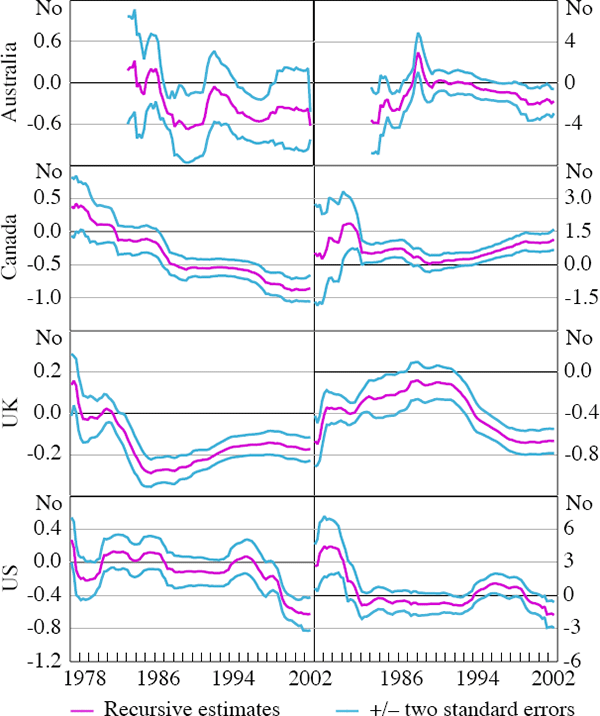
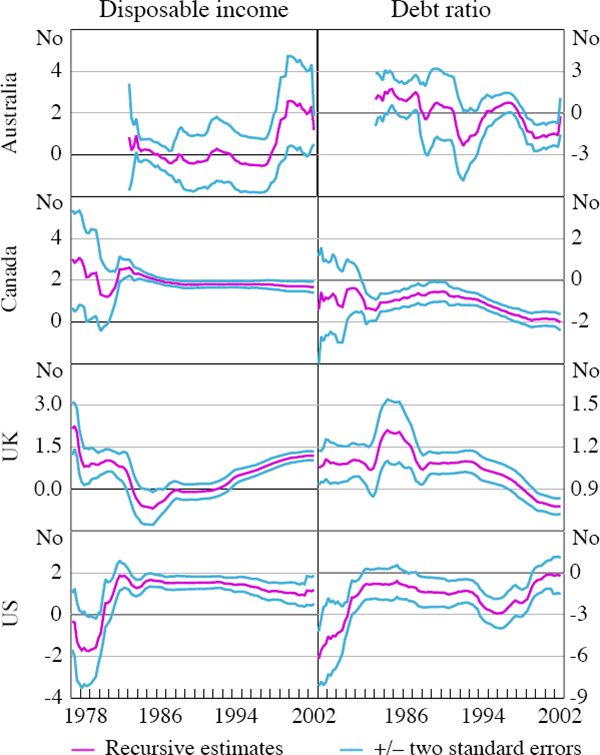
To assess the issue of instability in the estimates of Equation (4), recursive least squares estimation of the baseline specification was undertaken.[22] This was done excluding the dummy variables and over an expanding window. The starting sample is from 1970:Q3 to 1978:Q1 for all countries except Australia, for which the initial sample is from 1977:Q2 to 1984:Q1.
Results suggest that some parameter instability is present (Figures 3a and 3b). The absolute size of the long-run coefficient on equity prices increases towards the end of the sample period for Canada and the US (likely a result of a widening of equity holdings across households), with a similar pattern for house prices in the case of the UK and the US. Abstracting from instability early in the recursive estimation generated by the initially small sample sizes, only in the case of Canada do the coefficients on equity and house price terms appear to show clear linear trends throughout the expanding estimation window. For the case of the US, recent years have seen an increase in the effect of both equity and house prices on saving. For the UK, it would appear that, for the effect of housing prices on savings, there may have been a structural break in the early 1990s. For the income coefficients, recursive estimation indicates broadly stable parameter estimates for Canada and the US, whilst there is evidence of a break in the late 1990s in Australia and some drift in the case of the UK. Recursive estimation indicates an increase in the absolute value of the debt ratio coefficient in the cases of Australia, Canada and the UK in recent years.
3.3 A Panel of English-speaking Industrialised Countries
As a further step, the four countries are grouped into a panel in order to assess common trends. The estimation methodology employed is panel DOLS.[23] The estimation period is 1977:Q1–2002:Q1 in order to obtain a balanced panel. The panel unit root tests of Breitung (2000) indicate that all of the variables can be considered as I(1) stochastic processes in a panel context, while ADF tests for the error terms from the regression in log-levels indicate that the system has a cointegrating relation.
Results are presented both for the case of common constants and with cross-section fixed effects. On the basis of the estimation reported in Table 2, the following observations can be drawn:
| Estimation in
log-levels 1977:Q1–2002:Q1 |
Estimation in log difference 1977:Q2–2002:Q1 |
||||
|---|---|---|---|---|---|
| (1) | (2) | (1) | (2) | ||
| Constant |
2.367 (0.00) |
0.906 (0.71) |
|
||
| ECM(−1) |
|
−0.198 (0.00) |
−0.244 (0.00) |
||
| Disposable income |
1.073 (0.00) |
1.414 (0.00) |
|
9.236 (0.00) |
9.140 |
| Equity price index |
−0.783 (0.00) |
0.777 (0.00) |
|
−0.350 (0.04) |
0.360 (0.03) |
| House price index |
−0.372 (0.03) |
−0.462 (0.02) |
|
−2.124 (0.00) |
−2.277 (0.00) |
| Debt-income ratio |
−0.031 (0.36) |
−0.485 (0.00) |
|
0.344 (0.00) |
0.280 (0.02) |
| Adjusted R2 | 0.96 | 0.96 | 0.37 | 0.39 | |
| Notes: ECM(−1) indicates lagged error term from level equation. (1) is a regression with common constants; (2) with cross-section fixed effects. P-values are in parentheses. | |||||
- the estimated long-run cointegration equation indicates that disposable income enters the specification significantly and with the expected positive sign. Long-run income elasticities appear to be unitary when including a common constant, and somewhat higher when including cross-section fixed effects. The associated common marginal propensity to consume appears consistent with the average marginal propensity to consume from the country regressions in Section 3.2;
- an examination of the long-run wealth effects indicates that the equity price indices appear to have a larger long-term effect on real saving than those for house prices, with the converse true for the short run. This stands in contrast to the individual country results, though this result is likely driven by Canada, where house prices were estimated to vary positively (albeit insignificantly) with saving; as argued earlier, this latter result may stem from some instability in the Canadian housing price index in the late 1980s. All in all, it would appear that such a homogenous grouping of countries confirms the existence of a significant negative effect of wealth on saving;
- the estimated long-run coefficient on the debt-to-income ratio indicates a negative effect of financial innovation on saving; and
- the speed of adjustment term in the dynamic equation would indicate that cointegration holds in all cases, and points to a fairly rapid adjustment to long-run equilibrium in four or five quarters.
Footnotes
Other English-speaking industrialised countries with potentially similar features, such as Ireland and New Zealand, could not be included in the analysis given an incomplete quarterly dataset. [12]
This would include voluntary personal pension plans in the US and Canada, compulsory superannuation in Australia and a mix between voluntary and mandatory occupational personal pension plans in the UK. [13]
A log-linear specification is chosen over a per-capita alternative on two main grounds. First, the interpretation of parameter estimates from a log-linear specification is straightforward, while defining an appropriate per-capita specification is complicated by differing units of national accounts data versus asset price indices. Second, the quarterly data contain only positive values of saving over the sample period, allowing for the use of logarithms. [14]
Disposable income is the variable chosen in this study, rather than wages, given better data availability. Also, income other than wages and salaries (for example, interest and dividend income) contribute to saving. [15]
Even so, these price series appear to correlate highly with the available household wealth data. An examination of household net financial wealth and non-financial assets (as reported by the OECD Economic Outlook for Canada, the UK and the US; and the RBA for Australia) against the equity and house price index of the BIS, respectively, indicates a correlation of over 0.9 between each pair of series over the 1993–2002 period. [16]
These marginal propensities to save are obtained by multiplying the estimated income elasticity of saving by the average share of real household saving in real disposable income over the relevant sample period. [17]
For Australia, the numbers are somewhat below the estimates of Connolly and Kohler (2004), who find that the marginal propensity to save out of labour income is around 13 cents in the dollar. For the US, these implied marginal propensities are broadly consistent with the findings of Juster et al (2004), who find that an extra dollar of income raises saving by roughly 8 cents. Dynan et al (2004) find widely differing marginal propensities to save across households by income level, with estimates ranging from 3 cents per dollar of income for lower quintiles and up to 43 cents for upper quintiles. [18]
This finding is consistent with Case, Quigley and Shiller (2001), who show that housing wealth has a larger impact than equity wealth on consumption on the basis of a pooled sample of 14 countries. However, this result is not uncontroversial. It stands in contrast to the finding of Juster et al (2004), who use US microdata to show that the effect on saving of capital gains on corporate equities was substantially larger than the effect of capital gains on housing or other assets over the period 1984–1994. See Altissimo et al (2005) for a comprehensive review of the literature estimating wealth effects on consumption. [19]
Lettau and Ludvigson find that only a small fraction of the variation in household net worth over the past few decades has been related to variation in aggregate consumer spending, consistent with consumption smoothing – though this result is contested by Rudd and Whelan (2002). [20]
Another issue is that of possible simultaneity, although the assumption that asset values as weakly exogenous appears to be a reasonable approximation of reality given that saving from income that flows into wealth is eclipsed by valuation changes. An estimated restricted vector autoregression similar to that of Lettau and Ludvigson (2003) indicates some possible simultaneity for the US but not for the other countries (results available from author on request). [21]
This test is not without its faults – notably the low power to detect changes – but it has better performance in assessing the importance of structural breaks when compared with the Chow test when the date of the break is unknown (Hamilton 1994). [22]
See Mark and Sul (2002) for a recent discussion and application of this methodology. [23]