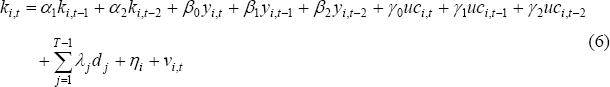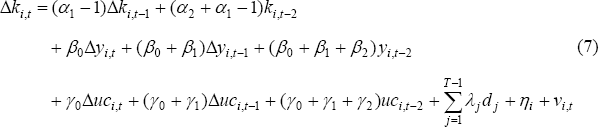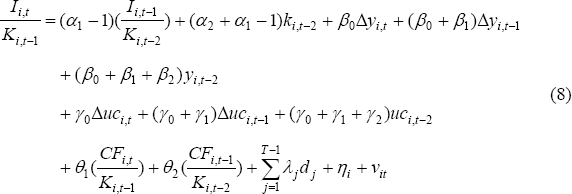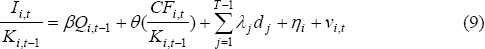RDP 2005-12: Financial Constraints, the User Cost of Capital and Corporate Investment in Australia 4. Modelling Strategy and Results
December 2005
- Download the Paper 530KB
4.1 Estimation Method
Investment is typically a dynamic process, either because firms must develop some expectation of the likely future profitability of a project and/or because the nature of adjustment costs implies that it is cheaper for a firm to adjust its capital stock gradually.[21] Models of business investment can generally be divided into two groups depending on whether the dynamics are modelled explicitly or implicitly. Explicit (or structural) models, such as the Tobin's Q and Euler equations, allow dynamic elements to appear explicitly in the firm's optimisation problem. These models have the benefit of directly linking the estimated coefficients to the underlying technology and expectation parameters (Chirinko 1993).
However, this paper focuses primarily on an implicit (or reduced form) model for several reasons. First, the main focus is to uncover the determinants of business investment rather than modelling the underlying technology or expectations formation processes. Second, while not explicitly derived, the investment equation still allows for short-run adjustment and expectation lags. Third, specifications similar to that used here have generally performed better than structural models in other microeconomic studies (Bond et al 1997; Chirinko, Fazzari and Meyer 1999; Von Kalckreuth 2001). Nevertheless, for comparability, I also estimate a Q-type model.[22] Such a model assumes that the rate of investment is a function of Q – the ratio of the market value of new investment goods to their replacement cost. Under certain restrictive assumptions Q can be empirically measured using equity market data (Bond and Van Reenen 2003).[23]
In constructing the main investment equation I start from the assumption that, in the absence of adjustment costs, the long-run equilibrium capital stock can be written as a (log-linear) function of real sales and the user cost of capital:
where ki,t is the (natural) log of firm i's desired capital stock at time t, ai,t is an intercept term that captures productivity shocks, yi,t is the log of real sales, uci,t is the log of the firm's user cost of capital and σ is the elasticity of substitution. This is consistent with profit maximisation subject to a constant elasticity of substitution (CES) production function and a single capital good. It allows for the possibility of constant returns to scale (ρ = 1), a fixed capital-output ratio (σ = 0), as well as the log-linear formulation with σ = 1, consistent with a Cobb-Douglas production function (Bond et al 2004).
The Error Correction Model (ECM) specification can be derived from this static capital demand equation. The procedure adopted here closely follows that of the existing literature (for example, Bond et al 1997). First, the equation is nested within a general dynamic regression model to account for the possibility of gradual adjustment of the capital stock to its long-run equilibrium.[24] Productivity shocks are controlled for by including time-specific and firm-specific effects:
where the dt's are dummies to capture time-specific effects, ηi is a firm-specific effect, νi,t is a white noise error term and the time series runs from t = 1 to t = T. An assumption of constant returns to scale would require the restriction (β0+β1+β2)/(1−α1−α2) = 1. Given the possible non-stationary nature of the data the equation is re-parameterised in error-correction form:
Letting Ii,t denote gross investment, Ki,t the capital stock, and δi,t the depreciation rate, we can then use the approximation Δki,t = (Ii,t/Ki,t−1−δi,t) to obtain an ECM specification for the investment rate (Ii,t/Ki,t−1).[25] To investigate the role of financial constraints, we also include current and lagged cash flow (CFi,t) terms in the equation.[26] The ECM becomes:
In Equation (8), the coefficient on the speed of adjustment term (α2+α1−1) is expected to be negative, as the firm should reduce investment if it has excess capacity. Financial constraints are modelled by augmenting the basic ECM of Equation (8) in one of two ways. The first is to use a dummy variable (DIVCUT) to identify financially constrained firms. This is equal to one if the firm has cut dividends (in either the current or previous year) and zero otherwise. This dummy is interacted with the cash flow variable to capture any differential effect of cash flow for financially constrained firms. These variables are denoted as DIVCUT*CF/K. The coefficients on the cash flow terms by themselves will capture the responsiveness of investment to cash flow for unconstrained firms (theory implies that these coefficients will be zero). The responsiveness of investment to cash flow for constrained firms is then given by the combination of the coefficients (θ1 and θ2) and the coefficients on the interactive DIVCUT*CF/K variables. The coefficients on these interactive terms are expected to be jointly significant and positively signed if financially constrained firms respond more strongly to cash flow than unconstrained firms.
As discussed in Section 2.2, the presence of distressed firms within the constrained group may bias the coefficient on these interactive terms. This bias could be significant given that negative cash flow (acting as a proxy for financial distress) occurs in around 15 per cent of the firm-year observations used in the model. The second way of augmenting the basic ECM attempts to deal with this problem by separating the financially constrained group into those earning positive and negative cash flow. This is done by the use of three separate dummies, again all interacting with the cash flow variable. The first dummy takes the value of one if the firm has cut dividends but earns positive cash flow (financially constrained, FC) and zero otherwise.[27] The second dummy takes the value of one if the firm has cut dividends and has made a loss during the year (financially distressed, FD) and zero otherwise. I include a third dummy for firms that have made losses but not cut dividends, a group I refer to as ‘loss-makers’ (LM). These firms are technically financially distressed but have not cut dividends, perhaps because they operate in industries that do not pay dividends (as we saw in Section 2.2) or because dividend cuts act as a signal of weak profitability to investors. The remaining group of firms that have positive cash flow are then classified as unconstrained (UC).
These two approaches are summarised in Table 1. The first approach divides the sample into two parts, those that have cut dividends (the first column) and those that have not (the second column). The second approach makes a further distinction by splitting firms on the basis of positive versus negative cash flow (the top and bottom rows respectively).
| Indicator of financial constraint | ||||
| Dividend cut | No dividend cut | |||
| Indicator of financial distress |
Positive cash flow |
346 (19.8%) FC – constrained |
1,141 (65.4%) UC – unconstrained |
|
| Negative cash flow |
98 (5.6%) FD – distressed |
160 (9.2%) LM – loss-makers |
||
| 1,745 (100%) | ||||
For comparability, I also estimate a structural Q-type Equation (Q1):
where all variables are as denoted before, with the addition of Qi,t−1 which represents the firm's average Q, measured as the market value of the firm's equity divided by the book value of the firm's equity. Constrained firms are accounted for by using the two sets of dummy variables described above. The results from estimating both the ECM and the Q model are outlined in Section 4.3. Before turning to the results, some econometric issues specific to panel-data models need to be briefly addressed.
4.2 Other Modelling Issues
Panel-data models are usually estimated using either ‘fixed effects’ or ‘random effects’ techniques. In this paper, a form of fixed-effects estimation is adopted because firm-specific effects are likely to be present, either as a result of technological heterogeneity or non-random sampling, with these likely to be correlated with the explanatory variables (for example, managerial skills could be correlated with the level of cash flow). This approach can yield consistent estimates even if the firm-specific error components and the explanatory variables are correlated.[28] This is the approach taken to estimate the Q model.
However, the issue is complicated in dynamic panels with a finite time horizon, such as the ECM. In this case, fixed-effects estimation is inconsistent because the lagged dependent variable is correlated with the error term. As a result, the ECM is estimated using the Arellano-Bond two-step Generalised Method of Moments (GMM) estimator which is consistent in this dynamic setting. This estimation technique eliminates firm-specific effects by differencing the equations, and then uses lagged values of endogenous variables as instruments. If the error term in levels is serially uncorrelated, then the error term in first differences is MA(1), and instruments dated (t−2) periods and earlier should be valid. Under this assumption, consistent parameter estimates can be obtained. The validity of the instruments is tested by reporting both a Sargan test of the over-identifying restrictions, and direct tests of serial correlation in the residuals.
4.3 Results
The complete list of coefficient estimates, standard errors, and levels of significance for four separate versions of the ECM are presented in Tables 2 and 3. The first model (EC1) is the standard ECM without cash flow in the formulation. The second model (EC2) then includes cash flow. The third and fourth models (EC3 and EC4) are as per EC2 but augmented with the two different sets of dummy variables interacted with the cash flow variable as described above.
| EC1 | EC2 | EC3 | EC4 | |
|---|---|---|---|---|
| Ii,t−1/Ki,t−2 | −0.31*** | −0.32*** | −0.32*** | −0.34*** |
| (0.06) | (0.06) | (0.06) | (0.05) | |
| ki,t−2 | −0.59*** | −0.59*** | −0.59*** | −0.52*** |
| (0.08) | (0.09) | (0.08) | (0.08) | |
| yi,t−2 | 0.23*** | 0.23*** | 0.23*** | 0.19** |
| (0.08) | (0.08) | (0.08) | (0.08) | |
| Δyi,t | 0.31*** | 0.31*** | 0.31*** | 0.27*** |
| (0.08) | (0.08) | (0.08) | (0.08) | |
| Δyi,t−1 | 0.21*** | 0.21** | 0.21*** | 0.16** |
| (0.08) | (0.08) | (0.08) | (0.08) | |
| uci,t−2 | −0.40** | −0.37** | −0.36** | −0.32* |
| (0.17) | (0.18) | (0.18) | (0.17) | |
| Δuci,t | −0.51*** | −0.50*** | −0.50*** | −0.49*** |
| (0.13) | (0.12) | (0.12) | (0.12) | |
| Δuci,t−1 | −0.29* | −0.27* | −0.27* | −0.27* |
| (0.15) | (0.15) | (0.15) | (0.15) | |
| CFi,t/Ki,t−1 | — | −0.04 | −0.04 | 0.24*** |
| (0.02) | (0.02) | (0.09) | ||
| CFi,t−1/Ki,t−2 | — | −0.00 | −0.00 | 0.16*** |
| (0.01) | (0.01) | (0.05) | ||
| DIVCUT*CFi,t/Ki,t−1 | — | — | 0.01 | — |
| (0.04) | ||||
| DIVCUT*CFi,t−1/Ki,t−2 | — | — | 0.04 | — |
| (0.03) | ||||
| FC*CFi,t/Ki,t−1 | — | — | — | −0.09 |
| (0.11) | ||||
| FC*CFi,t−1/Ki,t−2 | — | — | — | 0.06 |
| (0.06) | ||||
| FD*CFi,t/Ki,t−1 | — | — | — | −0.26** |
| (0.11) | ||||
| FD*CFi,t−1/Ki,t−2 | — | — | — | −0.16** |
| (0.06) | ||||
| LM*CFi,t/Ki,t−1 | — | — | — | −0.31*** |
| (0.10) | ||||
| LM*CFi,t−1/Ki,t−2 | — | — | — | −0.18*** |
| (0.06) | ||||
| Long-run elasticity of output growth | 0.40*** | 0.38*** | 0.39*** | 0.37*** |
| Long-run elasticity of the user cost of capital | −0.67** | −0.62** | −0.60** | −0.62** |
| Observations | 1,745 | 1,745 | 1,745 | 1,745 |
| Firms | 309 | 309 | 309 | 309 |
| Sargan Test | 0.10 | 0.09 | 0.22 | 0.41 |
| LM(2) | 0.32 | 0.22 | 0.24 | 0.58 |
| Notes: ***, ** and * denote statistical significance at the 1, 5 and 10 per cent levels respectively. Arellano-Bond GMM estimation. Estimated coefficients obtained from one-step estimators. Model specification tests obtained from two-step estimators. Robust standard errors in parentheses. Coefficients on constants are omitted. Sargan is a test for over-identifying restrictions (null hypothesis is to satisfy over-identification). LM(2) is a test for second-order residual serial correlation (null hypothesis is no serial correlation). Reported figures are p-values of the underlying test. Standard errors for estimated long-run elasticities are calculated using the delta method. | ||||
| Without cash flow in the regression | With cash flow in the regression | |||||
|---|---|---|---|---|---|---|
| Real sales | User cost | Real sales | User cost | Cash flow | ||
| US | na | na | 0.14* | −0.19* | 0.39 | |
| Japan | na | na | 0.08** | −0.10 | 0.06 | |
| France | 0.35* | −0.11* | 0.12** | −0.03 | 0.20** | |
| Germany | 0.45** | −0.66** | 0.39** | −0.52** | 0.08* | |
| Italy | 0.29** | −0.11** | 0.14** | −0.20** | 0.30** | |
| Spain | 0.14** | −0.26 | 0.02 | −0.28 | 0.15** | |
| Austria | 0.27** | −0.14 | 0.02 | −0.04 | 0.28* | |
| Belgium | na | na | 0.31** | −0.03** | 0.21** | |
| Luxembourg | 0.08** | −0.10** | 0.08** | −0.15** | 0.00 | |
| Hungary | na | na | 0.37** | −0.57** | 0.07 | |
| Australia | 0.40*** | −0.67** | 0.38*** | −0.62** | −0.02 | |
| Notes: ** and * denote significance at the 1 and 5 per cent levels respectively. The table has been adopted from Chatelain et al (2003). The results for the US were obtained from Chirinko et al (1999); from Nagahata and Sekine (2002) for Japan; and from Kátay and Wolf (2004) for Hungary. Estimation method is generally the two-step GMM in first differences. Significance levels determined by Wald tests on the sum of the coefficients appearing in the numerator. | ||||||
As can be seen in Table 2, the coefficient on the lagged investment rate is negative and significant across all four models, suggesting that investment is negatively correlated across successive time periods. This implies that ‘bursts’ of investment do not spill over to consecutive years, but are followed by lower investment rates in the future, on average. The speed of adjustment parameter is also of the expected (negative) sign implying that firms with excess capacity cut back on their investment plans.
The long-run effects of changes in the explanatory variables on investment in the ECM are also shown in Table 2. These long-run elasticities are calculated as the coefficient on the level term for the relevant variable divided by the (negative) coefficient on the level of the (log) capital stock. The long-run elasticity for the capital stock with respect to real sales is around 0.4. Assuming constant returns to scale, the long-run output elasticity should be close to unity. However, a Wald test suggests that the assumption of unit elasticity can be rejected. In other words, a given change in the capital stock appears to be associated with a larger change in sales, all else being equal. This is consistent with increasing returns to scale. The long-run elasticity for the capital stock with respect to the user cost of capital varies from 0.6 to 0.65 across the models.
In terms of the short-run effects, we can see that the coefficients on changes in real sales are positively signed and generally significant, with a strong contemporaneous effect. Impulse response functions (not illustrated) suggest that a rise in real sales leads to a contemporaneous rise in the capital stock, which is equivalent to about three-quarters of the long-run equilibrium adjustment. In the following year, the capital stock slightly overshoots this long-run level, before returning to be close to the long-run level in the third year. A similar dynamic response for the capital stock is also evident following a change in the user cost of capital.
In order to place these results in context, the estimated long-run elasticities from EC1 and EC2 can be compared with the results of some overseas studies (Table 3).
As can be seen from Table 3, the results are fairly comparable with the overseas studies. The point estimates for the long-run effect of sales on the capital stock are within the range of results for the European countries and the US. In contrast, I obtain a stronger effect for the user cost of capital than most other studies. Partly offsetting this, the effect of cash flow on investment appears weaker than that reported for the other countries. As discussed in the next section, this may reflect the underlying composition of the sample and, in particular, the presence of distressed firms.
Table 4 presents the results of estimating the Q model. As expected, the coefficient on the Q variable is statistically significant and positively signed across all three models, though the size of the effect of Q on investment is quite low. Such a finding is consistent with other studies (for example, Bond and Van Reenen 2003). Overall, the results appear reasonably comparable to those of the ECM.
| Q1 | Q2 | Q3 | |
|---|---|---|---|
| Qi,t−1 | 0.01*** (0.00) |
0.01*** (0.00) |
0.01*** (0.00) |
| CFi,t/Ki,t−1 | −0.01** (0.00) |
−0.01** (0.00) |
0.35*** (0.03) |
| DIVCUT*CFi,t/Ki,t−1 | — | 0.04* (0.002) |
— |
| FC*CFi,t/Ki,t−1 | — | — | 0.08 (0.07) |
| FD*CFi,t/Ki,t−1 | — | — | −0.39*** (0.04) |
| LM*CFi,t/Ki,t−1 | — | — | −0.37*** (0.03) |
| Observations | 2,595 | 2,595 | 2,595 |
| Firms | 391 | 391 | 391 |
| Within R2 | 0.081 | 0.084 | 0.142 |
| Notes: ***, ** and * denote statistical significance at the 1, 5 and 10 per cent levels respectively. Fixed-effects estimation. Robust standard errors in parentheses. Coefficients on constants are omitted. | |||
4.4 The Effect of Financial Constraints and Financial Distress
We are now in a position to assess the effect of financial constraints and distress on corporate investment in the models. In discussing the results, I generally focus on the preferred model, the ECM; most of the results from the Q model are broadly comparable.
Based on the results of the model EC2, cash flow appears to have a negligible influence on the investment rate, with the coefficients on cash flow negatively signed at both lags but not significantly different from zero (Table 2). Other parameter estimates appear robust to the inclusion of this variable. In contrast, the results of estimating the model Q2 suggest that the inverse relationship between cash flow and investment is statistically significant (Table 4). It is not clear why controlling for investment opportunities through the use of Q should necessarily lead to a significant negative correlation between cash flow and investment. It may simply reflect the fact that the size of the underlying sample differs between the two models, being somewhat larger in the Q model than in the ECM.
The effect of financial constraints can be examined more closely by comparing the coefficients on the cash flow terms in both the EC2 and EC3 models (Table 2). The coefficients on the CF/K terms remain statistically insignificant (and of the same magnitude) when separately accounting for constrained firms. The coefficients on the interaction dummies for constrained firms are also insignificant. These results imply that cash flow does not affect the investment of either unconstrained or constrained firms, on average.
Next, we assess whether the sensitivity of investment to cash flow for both constrained and unconstrained firms is affected by the presence of financially distressed and/or loss-making firms. Comparing the coefficients on the cash flow terms in the EC3 and EC4 models, the measured sensitivity of investment to cash flow appears to be the lowest for both distressed and loss-making firms (Table 2). In fact, the coefficient estimates imply that investment by firms with negative cash flow is relatively unresponsive to changes in cash flow. That is, the sum of the coefficients on the CF/K terms and the interactive FD*CF/K and LM*CF/K dummy terms is close to zero.[29]
Interestingly, separately accounting for negative cash flow observations effectively boosts the effect of cash flow on investment for both constrained and unconstrained firms.[30] However, splitting out these observations does not lift the effect of cash flow for constrained firms relative to unconstrained firms. Firms which are constrained (have cut dividends) but have positive cash flow (FC) appear to behave like unconstrained firms with positive cash flow (UC) in that their investment responds to cash flow by a similar order of magnitude. The notion that the investment of unconstrained firms is sensitive to cash flow is a common finding in the literature despite contradicting conventional theory (Cleary 1999; Kaplan and Zingales 1997). This result also appears fairly robust, as similar results are found for the Q model. While we cannot rule out the possibility that this result is due to not having a variable that adequately distinguishes between constrained and unconstrained firms, using other indicators of financial constraints (such as size, age and the presence of bond ratings) does not alter the main findings.
Footnotes
This is true, for example, in the case of quadratic adjustment costs. [21]
Despite being commonplace in micro studies of investment, the results of Q models have generally been disappointing, often giving unreasonably low estimates of the effect of Q on investment (Bond and Van Reenen 2003). Furthermore, it is difficult to separately identify the interest rate and credit channels in a Q-type investment function. In practice, observable (average) Q is calculated from firms' share prices, which are governed by fluctuations in asset prices and could therefore reflect either the interest rate or credit channel. [22]
See Appendix A for details on the construction of the Q measure. [23]
This implicitly assumes that the firm's desired capital stock in the presence of adjustment costs is proportional to its desired capital stock in the absence of adjustment costs, and that the short-run investment dynamics are stable enough over the sample period to be well approximated by the distributed lags in the regression model (Bond et al 1997). [24]
The term, Δki,t, is the change in the log(Ki,t) which is roughly equal to the percent change in Ki,t. This, in turn, is approximately equal to (Ii,t/Ki,t−1−δi,t). The depreciation rate, δi,t, can be subsumed into some combination of the last three terms in Equation (8), allowing Δki,t to be replaced with Ii,t/Ki,t−1. [25]
Heteroskedasticity can be a problem with company accounts data. The cash flow and investment variables are scaled by the previous period's net capital stock to minimise its effect (for example, through firm size effects). Estimating with robust standard errors should control for any additional effects of heteroskedasticity. [26]
Here, and in what follows, this refers to dividend cuts and cash flow of the current and the previous year. [27]
While a consistent estimator, the use of many dummy variables means the fixed-effects estimator is less efficient than the random-effects estimator. [28]
Wald tests on the estimated coefficients reveal that the effect of cash flow on investment for financially distressed firms is not significantly different from zero while the effect of cash flow on investment for loss-making firms is actually negative and significant at the 5 per cent level. [29]
See Appendix C for a detailed reconciliation of the findings of this paper and those of earlier Australian studies. [30]