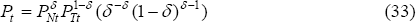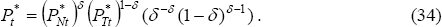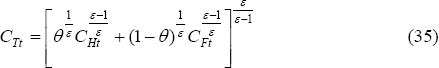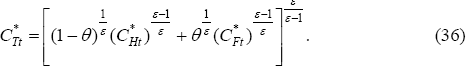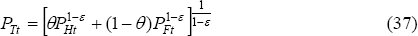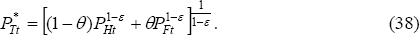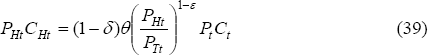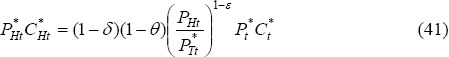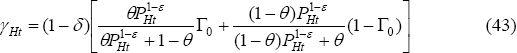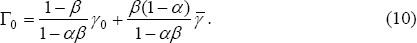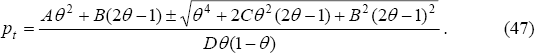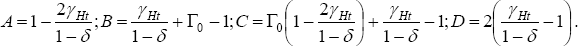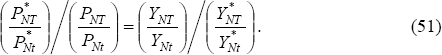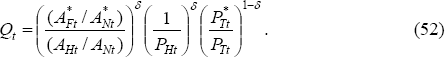RDP 2005-09: The US Current Account Deficit: A Re-Examination of the Role of Private Saving 3. Real Exchange Rate Model

Obstfeld and Rogoff (2000, 2004, 2005) have argued that the correction of the US current account will require a large real depreciation. It is interesting to examine what the evolution of the real exchange rate would be if the current account deficit was optimal, reflecting expectations of growth in the US's share of world-adjusted GDP. As in Obstfeld and Rogoff, we need to make some specific assumptions about preferences in order to derive results.

In each country, we assume that preferences are a Cobb-Douglas aggregate over a non-traded consumption good, and a traded consumption aggregate:

The exact price indices are given by:

Preferences over traded goods consumption are, in turn, a function of the consumption good produced in each country:

We assume here that preferences are symmetric, but that there is bias toward the consumption of the good produced locally (θ > 1/2 ).

Price indices are given by:

We have the following demand system:

We do not need to write down the demand for the foreign-produced traded good. We can ignore that market, because by Walras's law if the markets for the other three goods clear each period and the budget constraints are satisfied, then the market for the fourth good will also clear.

The equilibrium conditions at time 0 and in the long run are as follows. We set the price of the foreign-traded good equal to one in each period. We also will consider the simple case in which net debt at time 0 is zero. That is because, in applying this model to the US to examine how its real exchange rate will evolve, we will use the approximation that its current net investment income is zero:

Here we have defined γ_Ht and γ_Nt to be the value of the home country's output of traded goods and non-traded goods, respectively, as a share of the value of world output. It is helpful to notice from Equation (44) that because of the assumptions of unitary intertemporal elasticity of substitution and unitary elasticity of substitution between non-traded and traded goods, the value of each country's non-traded output as a share of world output is constant over time. We can write:

Now, as in the previous sections, assume a slow increase in the home country's output as a share of world output. Repeating Equations (9) and (10):

Then we can write:

We can now use these equations to solve for P_Ht. Define 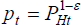. Given assumptions about y₀ and 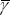, we can use Equation (10) to derive Γ₀, and Equations (9) and (46) to derive y_Ht. Equation (43) can then be shown to be a quadratic equation in p_t, whose solution is:

The parameters A, B, C, and D are defined by:

We can then derive P_Ht by using .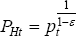

Ultimately, we are interested in calculating the home real depreciation over some time horizon from t to T, Q_T/Q_t, where 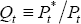is the CPI real exchange rate (defined so that a home real depreciation is an increase in Q_t). Using the definitions of the price indices Equations (33) and (34), we have:

Since we are setting P_Ft = 1, our solution for P_Ht allows us to solve for 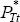and P_Tt.

Even though there is home bias in the consumption of the traded good, this is not a cause of the price of the home-produced traded good, P_Ht, changing over time. As we note below, in this model total consumption expenditure in both countries risesat the same rate, so the home bias does not put pressure on either traded goods price. But if the home country's share of world output is growing, then output of the home-traded good is growing faster than the output of the foreign-traded good, so its price must be falling.

What about the behaviour of the non-traded prices? If there were no home bias in consumption of the traded good, any change in the real exchange rate would have to come from movements in the relative non-traded prices. Indeed, Obstfeld and Rogoff (2000, 2004, 2005) emphasise the importance of the non-traded sector.

In our model of consumption, if the net factor income at time t is zero, from time t into the future we know that home and foreign nominal consumption will grow at the same rate:

(We are starting in period t, and T > t.) This result is actually quite general in the neoclassical model. That is, the result is based on the assumption that preferences are homothetic and that the intertemporal rate of substitution is the same in the two countries. This is less specific than the log specification that we have been using and does not require that preferences are the same in the two countries.

Now under our assumption that there is a Cobb-Douglas utility function defined over traded and non-traded goods we can write:

where P_Nt is the price of the non-traded good, and Y_Nt is the output of the non-traded good.

Now we can see how the price of non-traded goods at home changes relative to the price of non-traded goods in the foreign country:

The change in our non-traded price relative to the foreign non-traded price depends only on the growth rates of the non-traded goods. It does not depend at all on the shares of non-traded goods in consumption.

While our optimising model can potentially explain a current account deficit if the country's share of world output is expected to rise over time, under the Cobb-Douglas assumption, none of that increase can come because the value of non-traded output rises as a share of world output. We have noted that γ_Nt is constant over time. The assumption that our share of world output is rising does not require any assumption on whether the home country's non-traded output growth is faster or slower than in the rest of the world.

We consider two models for 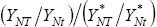. The first is simply an endowment model, as in Obstfeld and Rogoff (2004). The second model is one in which output is produced using labour, and the growth rates of productivity in the traded and non-traded sector determine .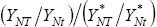

In that model, output of the traded sector in the home country is given by Y_Ht = A_HtL_Ht, and in the non-traded sector by Y_Nt = A_Nt(L − L_Ht). Here, A_Ht and A_Nt represent productivity, which may grow over time. These equations incorporate labour market equilibrium, with the assumption that the labour supply is fixed and equal to L. If labour markets are competitive, then we have P_Nt/P_Ht = A_Ht/A_Nt , or P_Nt = (A_Ht/A_Nt)P_Ht. Similarly in the foreign country, we get .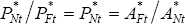

We then have:

On the one hand, we have argued that if the home country's output of the traded good is growing more quickly than the foreign country's, then P_Ht must be falling. That implies that the (1/P_Ht)^δ term in Equation (52) must be rising. In addition, if there is home bias in consumption of traded goods, the 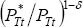term is also rising. Both contribute to a real depreciation for the home country. But working in the other direction is the fact that the relative growth in the home country's traded output is coming from productivity growth in the traded sector. 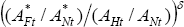Unless home's relative growth advantage in the non-traded sector is greater than its relative growth advantage in the traded sector, will be falling. This is the standard Balassa-Samuelson effect. This latter effect might well outweigh the first two effects, so in net terms the home country could be experiencing a real appreciation along the adjustment path as its current account deficit declines.