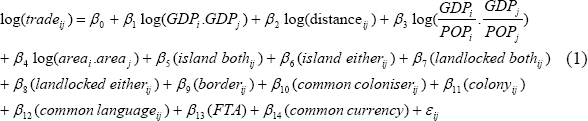RDP 2004-11: Trade Openness: An Australian Perspective 2. The Gravity Model
December 2004
- Download the Paper 498KB
2.1 Background
The most common framework for explaining observed trading patterns is the gravity model (see, for example, Frankel 1997, Rose 2000, and Anderson and van Wincoop 2003). The underlying premise of the gravity model is that bilateral trade is a function of the geographic distance between two countries (which is a proxy for transport costs), and the two countries' combined economic size, measured as the product of the two GDPs. Typically, a number of other variables – to capture geographic features, economic development and policy institutions – are also included as regressors when estimating the model.
The gravity model is a powerful tool for testing a variety of hypotheses, such as the effect of a common currency or membership in a common free trade agreement on bilateral trade (see, for example, Rose 2000). While it is generally used to explain bilateral trade between countries, the estimated gravity equation can, in principle, yield implications about aggregate country trade. For example, one could ask how well aggregate trade levels are explained by those variables that the gravity literature suggests are empirically important determinants of bilateral trade. Indeed, the goodness of fit of the gravity model at the aggregate country level is arguably an important aspect of the model's overall adequacy.
There are two ways in which the gravity model's goodness of fit for a particular country could be assessed. The first would be to add a country-specific dummy variable to the bilateral model. If the dummy variable is economically and statistically significant, it can be concluded that the model provides a relatively poor fit for the particular country. A second approach would be to take the (de-logged) fitted values of bilateral trade from the model, sum up these values for each country and then compare this with each country's actual trade. We consider both approaches in Section 2.3.
2.2 Estimation with the Bilateral Gravity Model
To estimate a gravity model we use the extensive data set compiled by Andrew Rose.[5] This contains data on numerous variables for over 170 countries and territories. We begin by estimating a fairly standard ‘empirical’ gravity model, as opposed to the ‘theoretical’ gravity model proposed by Anderson and van Wincoop (2003). The model is similar to Rose (2000), and uses typical economic and geographical variables and also a number of dummy variables. The estimated equation is:
where i and j are the two countries in the bilateral trading relationship. The dependent variable tradeij is defined as nominal trade in both goods and services, deflated by the US chain price index (see Rose 2000 for more details). We have estimated this equation for six five-year periods going back to 1970, but for brevity present the results for only one cross-section regression with data averaged over 1995–1999, the last five years in the Rose data set. The results are in column (1) in Table 1.
| (1) | (2) | |
|---|---|---|
| Product of total GDP | 1.03*** (0.01) |
1.05*** (0.01) |
| Distance | −1.23*** (0.03) |
−1.30*** (0.03) |
| Product of per capita GDP | 0.19*** (0.02) |
−0.03* (0.02) |
| Product of area | −0.11*** (0.01) |
−0.10*** (0.01) |
| Island both | 0.63*** (0.13) |
0.73*** (0.13) |
| Island either | −0.16*** (0.05) |
−0.01*** (0.05) |
| Landlocked both | 0.49*** (0.13) |
0.35*** (0.12) |
| Landlocked either | −0.57*** (0.05) |
−0.71*** (0.05) |
| Common border | 0.96*** (0.14) |
0.85*** (0.14) |
| Common coloniser | 0.42*** (0.09) |
0.53*** (0.09) |
| Colony | 1.36*** (0.13) |
1.17*** (0.13) |
| Common language | 0.37*** (0.06) |
0.46*** (0.06) |
| Common FTA membership | 0.88*** (0.13) |
0.57*** (0.13) |
| Currency union | 1.04*** (0.22) |
1.07*** (0.23) |
| Trade liberalisation index | 0.44*** (0.02) |
|
| Number of observations | 9,637 | 9,637 |
| Adjusted R2 with dependent variable defined as log(tradeij) | 0.72 | 0.73 |
| Adjusted R2 with dependent variable defined as log(tradeij/(GDPi GDPj)) | 0.34 | 0.37 |
| Memo item: Dummy variable for Australia |
0.40*** (0.12) |
0.20 (0.12) |
|
Notes: Besides the memo item, all the results are for regressions excluding the Australian dummy variable. Robust standard errors are shown in brackets. Significance at the 1, 5 and 10 per cent levels is denoted by ***, ** and *, respectively. Estimates for the constant are omitted for brevity. |
||
The results in Table 1 are typical of gravity models. The adjusted R2 of above 0.70 suggests that the overall fit of the model is good for such a large cross-section. All variables are also significant at the 1 per cent level. Bilateral trade, as expected, is strongly positively related to the two countries' economic size (measured by the product of GDPs). After the product of GDPs, the second most significant variable in explaining bilateral trade (in terms of the explanatory power added to the equation, and regardless of ordering), is the distance between two countries, which takes the expected negative sign. This is presumably because trade costs, especially transport costs, increase with distance. Bilateral trade is also estimated to be positively related to the stage of development (proxied by the product of GDPs per capita). Trade is negatively related to combined geographic size, presumably because geographically larger countries are more likely to be self-sufficient (especially in primary products) and thus trade less. (As they are not central to the paper, we do not discuss the coefficients on the dummy variables, although all are significant at the 1 per cent level and most take the expected sign.)
Column (2) of Table 1 shows the results of estimating Equation (1) with an extra variable, which is the average of indices for the 1995 trade-policy regimes of the two trading partners. The trade-policy variable is described in more detail in Section 3, but is calculated so that it is higher for countries with more liberal trade regimes. The main impact of the inclusion of this variable is to change from positive to negative the parameter estimate on the variable for the product of the per capita GDPs. However, we defer further discussion of this finding until Section 3.3.
2.3 Assessing the Overall Fit of the Gravity Model
The results in Table 1 suggest that the gravity model fits the data well. However, two points deserve further attention. First, it is perhaps not surprising that the product of GDP variable is so strongly significant (the t-statistic in column (1) is above 80), as trade will clearly be greater between bigger economies. Accordingly, it may be of interest to examine the overall fit of the regression absent this scaling effect. Second, while the overall fit of the model for bilateral trade flows is good, it remains to be considered how well the model fits particular countries.
To assess the influence of the product of the two countries' GDP as a regressor in the gravity model, we re-estimated the model with the dependent variable divided by the product of the two countries' GDP, with all of the independent variables remaining unchanged. The resulting adjusted R2 of 0.34 indicates that a substantial proportion of the original goodness of fit is due to the scaling effect of economies' sizes. Another way of illustrating this point is the fact that a regression of bilateral trade on just a constant and the product of GDPs yields an adjusted R2 of 0.57, so that once one has controlled for the product of GDPs, the additional 13 variables contribute only an additional 0.14 points to the overall adjusted R2.
To assess the fit of the model at the aggregate level for each country, two approaches were used. The first involved estimating Equation (1) separately for each country with a country-specific dummy for that country. The coefficients on the dummies provide one gauge of how well the gravity model fits a particular country's bilateral trade: a zero value implies a perfect fit, a positive value implies actual trade is above fitted trade and a negative value implies actual trade is below fitted trade. The second approach involved creating fitted values for bilateral trade between every pair of countries, de-logging the data and then summing up for each country to create a fitted value for aggregate country trade.[6] The computed ratio of actual total trade to fitted total trade provides a further method to see whether countries' aggregate trade is similar to the level that might be expected. Figure 2 presents the two measures in a scatter plot: the ratio from the second method is converted into logs for comparability.
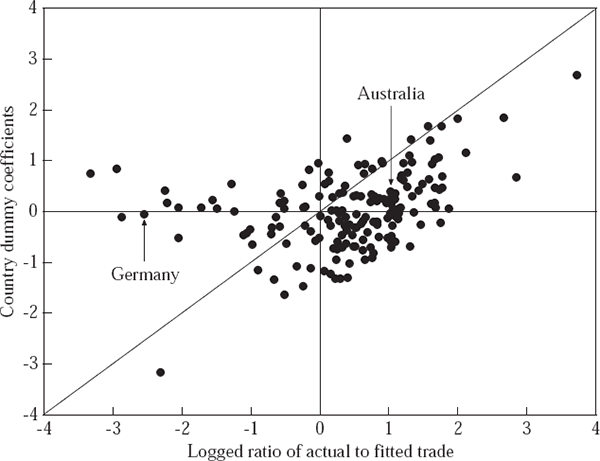
If the gravity model provided accurate predictions of aggregate country trade, the dots would cluster around the origin of Figure 2. Further, if the two methods for assessing the gravity model's goodness of fit at the country level presented similar conclusions, the dots should cluster around the 45 degree line. However, the relationship between the two measures is not that strong, with a correlation coefficient between the two measures of only 0.38. Indeed, for 78 of the 173 countries, the two approaches would suggest different conclusions about whether the total trade of a country is more or less than predicted. In some cases the two approaches provide sharply conflicting results. An extreme example is the case of Germany, where actual trade is around 1/13th of summed fitted trade,[7] while the dummy variable coefficient of −0.06 (which is not significantly different from zero) suggests that Germany's bilateral trade levels were on average only about five per cent smaller than implied by the gravity model results for other countries.
One reason the two approaches frequently yield different answers is that the ‘dummy variable’ approach places equal weight on a country's trade with all of its trading partners, while the ‘fitted values’ approach implicitly places more weight on the ability of the gravity model to explain a country's trade with larger countries. In the case of Australia, both methods suggest that Australia trades substantially more than would be predicted by the gravity model, but by substantially different magnitudes. When a country dummy is added to the gravity model it takes the value of 0.40, suggesting Australia's bilateral trade levels were on average nearly 50 per cent higher than implied by the gravity model results for other countries. Alternatively, when all the fitted values for Australia's bilateral trade are summed together, they indicate that Australia's trade is around 2.8 times that predicted by the gravity model. The reason for the latter result is that Australia tends to trade more than predicted with large countries and less than predicted with smaller countries. Indeed, Australia trades more than the gravity model predicts with the 14 largest countries in the database, which account for 82 per cent of rest-of-world GDP. It is tempting to conclude that Australia trades more than predicted by standard empirical models of trade and indeed has had the good fortune to have generated stronger trading links with the world's larger economies. However, before reaching any conclusions on these issues, we consider an alternative approach to the question of how well we can explain the aggregate level of trade undertaken by individual countries.
Footnotes
The data (with definitions) are available at <http://faculty.haas.berkeley.edu/arose/RecRes.htm>. [5]
Frankel and Romer (1999) also follow this approach (although based only on geographic variables) to generate fitted values for total trade. [6]
The gravity model suggests very high levels of trade between Germany and its immediate neighbours. Indeed it suggests that trade with nine neighbours should account for 84 per cent of Germany's total trade. Germany does trade heavily with these countries, but in reality they account for ‘only’ 40 per cent of its total trade. [7]