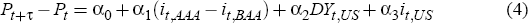RDP 2004-07: The Profitability of Speculators in Currency Futures Markets 4. Explaining Speculator Profitability
September 2004
- Download the Paper 143KB
In this Section we examine the two classes of explanations for speculator profitability discussed in Section 1 – a premium for bearing risk, and the use of technical trading rules. It is important to note that the data we use in this study are the market price of futures and the quantity held by speculators and hedgers. Without further assumptions we cannot back out from these data the underlying demand relationships for each of the trader groups. Given this, our explanation of speculator profitability is one of reduced form, not structural, relationships.
4.1 A Premium for Bearing Risk
In an asset-pricing model such as the CAPM individual assets pay a risk premium if their returns are correlated with the return on the market portfolio. Stein (1986) and others have argued that asset-pricing models such as CAPM don't apply to futures because they are in zero net supply – for each long position there is a short position – and so they are not in the market portfolio. In any case, as Table 5 shows, gross speculator returns from futures positions are essentially uncorrelated with US stock and bond index returns. That is, the returns to speculators do not appear to be ‘risky’ in the sense of having a positive correlation with standard risk factors.
| S&P 500 Composite index | US bond return index | |
|---|---|---|
| Australian dollar | 0.07 (0.21) |
0.08 (0.32) |
| British pound | 0.00 (0.99) |
0.04 (0.56) |
| Canadian dollar | 0.03 (0.44) |
−0.04 (0.03) |
| German mark/euro | −0.07 (0.20) |
0.05 (0.26) |
| Japanese yen | −0.02 (0.42) |
−0.02 (0.59) |
| Swiss franc | −0.01 (0.42) |
−0.01 (0.52) |
|
Notes: The US bond index is for bonds of all maturities, rated A or above. |
||
Even though currency futures are not risky, in that they are uncorrelated with other assets, they still have idiosyncratic risk. This matters as currency futures may be a large part of a trader's portfolio. Hedgers, as a group, may be looking to offload the idiosyncratic risk of their fundamental exchange rate exposure. So one justification for speculators' profitability is that hedgers will pay a premium to induce speculators to take on these risks. Any premium received by speculators will come in the form of a positive expected return on their positions. This intuition has long been applied to physical commodity markets as an argument for futures prices to be backwardated, that is, hedgers generally take short positions so prices rise as they near expiration to compensate speculators for taking offsetting long positions. For a summary of this argument in physical commodity markets see Kolb (1992).
We explore the risk premium as an explanation of speculator profits through the predictability of returns. If returns could easily be predicted by the market then the transfer of predicted returns between traders can be seen as a risk premium. However, the predictability of returns is not conclusive evidence of a risk premium. It could be that traders use different models to generate their expectations of futures price movements and one group, speculators, is more successful. We consider such an explanation in Section 4.2. For now, we examine whether speculators' positions move in line with our particular model-based predicted returns. We then test whether speculators make profits after adjusting for predicted returns.
4.1.1 Calculating predicted returns
Bessembinder and Chan (1992) showed that returns on currency, agricultural and metal futures could be partly explained by several risk factors. We follow Bessembinder and Chan in using US dividend yields, interest rates and corporate spreads to generate a series of predicted returns. We estimate the coefficients in Equation (4) using information available at time t and then use these coefficient estimates and the risk factors at time t to generate out-of-sample predicted changes in futures prices looking forward from time t:
where it,AAA and it,BAA are the Moody's AAA and BAA corporate bond rates, DYt,US is the US dividend yield, it,US is the US euro interest rate and Pt is the price of the next to expire futures contract. We use three-year rolling regressions to account for possible changes in the way our risk factors affect predicted returns.[10]
From Equation (2) traders need to predict both the end of the week price (Pi,t+5) and the intermediate price (Pi,[t,t+5]) to find their expected profits of a particular trading strategy. We therefore run regressions of Equation (4) for Pt+Τ equal to both Pt+5 and P[t,t+5]. Note, we run these regressions only for the first to expire contract and then assume that the returns will be the same for all other trading contracts.[11]
Weekly predicted price changes are small (about 0.3 per cent) relative to actual changes in futures prices (typically around 1 per cent) and are also much more persistent. There is only a weak relationship between predicted and actual price changes, as shown by the small and insignificant correlation coefficients in the first column of Table 6. This is not surprising given the volatility of futures returns and the general inability to predict exchange rate changes out of sample, and accords with earlier work.
| Weekly predicted price changes (Correlations and p-values) |
Predictability of profits (Weekly average, US$ millions) |
||||
|---|---|---|---|---|---|
| Actual price changes |
Net speculator position |
Predictable profits |
Abnormal profits |
||
| Notes: Price changes are in per cent. Gross profits are used. P-values in parentheses are generated by Monte Carlo simulations. Rejections of the null that a coefficient is insignificantly different from zero are shown in bold. |
|||||
| Australian dollar | 0.07 (0.11) |
0.50 (0.00) |
0.67 (0.00) |
−0.22 (0.29) |
|
| British pound | 0.01 (0.72) |
0.26 (0.04) |
1.05 (0.00) |
−1.01 (0.05) |
|
| Canadian dollar | −0.15 (0.00) |
0.43 (0.00) |
0.48 (0.00) |
0.10 (0.76) |
|
| German mark/euro | 0.06 (0.17) |
0.38 (0.01) |
3.07 (0.00) |
1.46 (0.21) |
|
| Japanese yen | 0.02 (0.58) |
0.29 (0.02) |
4.20 (0.00) |
1.16 (0.54) |
|
| Swiss franc | 0.04 (0.36) |
0.48 (0.00) |
2.71 (0.00) |
−0.85 (0.26) |
|
Despite the low forecasting power of our model, there is a significant positive relationship between net speculator position and weekly predicted price changes (second column of Table 6). When our model predicts a price increase speculators take longer positions. This is suggestive of speculator profits being a risk premium – hedgers transfer expected returns to speculators as compensation for transferring currency risk.
Next we consider what proportion of speculators' profits is compensation for the transfer of risk. In order to calculate predicted returns we need not only predicted prices but also the positions held by the traders. In the absence of intra-week positions data, we assume that speculators commit to a trading strategy at the beginning of the week when they calculate the expected returns. This allows us to use realised position data to calculate expected profitability. The third and fourth columns of Table 6 divide speculator profits into the part that is predictable, using our model, and the part that is not. The predictable part is found by combining forecast futures prices found by Equation (4) with actual speculator positions in the profit calculation from Equation (2). The unpredictable part of profits is then the difference between total profits and predicted profits. Predictable profits accounts for most of actual profits, and are significantly greater than zero for all currencies. Abnormal profits is often negative and in no cases is it significantly greater than zero. These results suggest that speculators' profits could be a transfer for bearing risk. An alternative explanation is that speculators form more accurate expectations of changes in futures prices, in particular it could be that they use better forecasting techniques. One such possibility is technical trading rules, to which we know turn our attention.
4.2 Trading Rules
There is an extensive literature documenting the use of trading rules by traders in exchange rate markets, notably surveys of market participants by Taylor and Allen (1992), Menkhoff (1998), Cheung and Wong (2000) and Lui and Mole (1998). Traders are also reported to place more emphasis on these rules over short horizons, such as the one-week changes we consider here. Many studies, including Taylor (1992), have also demonstrated that a wide range of trading rules can be profitable in foreign exchange markets. The finding that such rules are profitable is subject to the criticism of data mining, particularly when complicated rules are constructed ex post, as in Neely, Weller and Dittmar (1997). However, the long history of trading rules in the exchange rate forecasting literature, for example Goodman (1979) and Sweeney (1986), suggests trading rules may have some value. While there are many different trading rules, the common element to such rules is that they respond to past price changes, with most rules implying a position that positively correlates with past returns.[12] For many rules this dependence on past returns will be non-linear, for example switching between long and short positions based on different length moving averages crossing each other.
If speculators are using such rules we would expect their net positions to be related to past futures returns. We therefore test whether speculators' net positions, in either levels or changes, lag currency futures returns, measured as the change in the price of the next to expire contract. A finding in favour of this hypothesis would be suggestive, but not conclusive, evidence that speculators use these rules. Nor would it necessarily imply that the use of these rules explains speculators' profits. It could be instead that hedgers also use these techniques to produce equally accurate forecasts, but that they take a less profitable position because they are paying speculators a premium to bear risk, as discussed in Section 4.1.
Table 7 reports the probabilities (p-values) from Granger causality tests of futures returns leading net positions. The signs below each of the p-values show the sign of the sum of the coefficients on the three lags of the change in futures prices, the ‘causing’ variable. For all currencies we reject the null hypothesis that futures returns do not lead the level of net speculator position. For four of the currencies futures returns are also found to lead the change in net speculator position. With only one exception, the sign on the lagged exchange rate is positive. This indicates that speculators have a longer net position, and increase that position, if there have been positive returns to holding futures in the past.
| Null hypothesis | AUD | GBP | JPY | CAD | CHF | DEM/EUR |
|---|---|---|---|---|---|---|
Δf 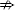 ΔnetS ΔnetS |
0.00 + |
0.16 + |
0.32 + |
0.00 + |
0.06 + |
0.05 − |
Δf 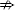 netS
netS |
0.00 + |
0.00 + |
0.07 + |
0.00 + |
0.00 + |
0.02 + |
|
Notes: Sample 05/01/1993 to 18/02/2003 (weekly) |
||||||
One interpretation of this positive relationship is that speculators are positive feedback traders, increasing their net position when there have been positive returns to being long in that currency future, possibly because they are using trend-following trading rules. If this is the case, the fact that we find a linear leading relationship would imply that the aggregate degree of non-linearity in trading rules is not too large. Of course, the observed futures return and net speculator position is an equilibrium outcome involving speculators, hedgers and small traders. So the positive leading relationship of speculator net position by returns could alternatively be attributable to the rest of the market being negative feedback, or contrarian, traders. What we can conclude is that relative to the market as a whole, speculators are positive feedback traders. We take this as evidence that speculators most probably use trend-following trading rules.
Footnotes
The regressions are run using OLS, but the results do not differ if instead we use SUR to account for possible correlation of residuals across currency equations. [10]
This assumption seems reasonable since, as noted in Section 2, the weekly returns on contracts with different expiration dates for a given currency have a correlation over 0.99. [11]
Some trading rules also depend on volume indicators. [12]