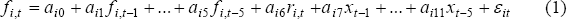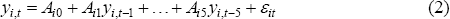RDP 2004-05: Big Fish in Small Ponds: The Trading Behaviour and Price Impact of Foreign Investors in Asian Emerging Equity Markets 3. How Are the Net Purchases of Foreign Investors Related to Prior Returns?
June 2004
- Download the Paper 624KB
3.1 Introduction
Daily data allow a very precise analysis of the short-term determinants of net investor demand. In particular, if net purchases by foreigners (or any other group of investors) respond systematically to recent returns, daily data should be able to capture these linkages. The most comprehensive work to date in this area is by Froot et al (2001) who find strong evidence that flows into a market are positively correlated with lagged returns in that market. They suggest that this positive-feedback trading may be evidence that some foreign investors use returns to extract information about future returns.
However, as is discussed in Section 3.2, it is also plausible that flows into a market could be driven by returns in other markets, so that the Froot et al bivariate empirical model might be too restrictive. Indeed, given that returns in different markets are positively correlated, there is a possibility that the significance of lagged domestic returns may actually be proxying for the effect of lagged returns in foreign markets. Hence, the strategy in this section will be to confront the flows data with a group of returns series, and find which of these series can best explain flows. VAR systems including foreign returns are then estimated to get a more complete picture of the dynamics of the impact of returns on flows.
3.2 Regression Analysis of the Effect of Returns on Inflows
This section begins by proposing several different types of returns that might plausibly influence the net inflows of foreigners into Asian emerging equity markets. The possible explanators of inflows include:
Returns in the domestic market: Models such as Brennan and Cao (1997) suggest that if foreigners have an informational disadvantage in emerging markets, they may use recent returns as an input in forming their expectations about future returns. Hence, net inflows may be partly explained by lagged domestic returns. In each case, domestic returns are proxied by the capitalisation-weighted index for the total market, in local currency.[8]
Returns in major mature markets: Investors in large mature markets might increase their allocations to emerging markets following increases in their home markets, due to portfolio rebalancing effects. For example, Stulz (1999) notes that it may be perfectly rational for US investors to invest more in emerging markets when their wealth increases, and Griffin, Nardari and Stulz (2003) propose a model that contains such an effect. Alternatively, returns in mature markets might influence flows because investors extract information from global returns about prospects for emerging markets. Finally, a response of flows to returns in global markets may be more behavioural, and based more on sentiment than rational information extraction. These possibilities are tested by the inclusion of daily returns on broad portfolios of US stocks (the S&P 500 index) and stocks in all mature markets (the MSCI World index), both expressed in US dollars.
Returns in all emerging markets: Much investment in emerging markets occurs not via managers with a global mandate but rather via specialist managers investing only in emerging markets.[9] Hence if portfolio rebalancing effects are important, the relevant return might not be a global mature markets return, but rather the return on a basket of emerging market equities. Accordingly, the return on a broad emerging markets index (the MSCI Emerging Markets Free index) is also included as a possible explanator.
Returns on US technology stocks: Several markets in Asia are highly dependent on the global technology sector. For example, Taiwan and Korea are the homes of companies (Taiwan Semiconductor and Samsung Electronics) that are – by many measures – the world's two largest semiconductor companies.[10] Hence, news about technology stocks in global markets represents news about ‘fundamentals’ that might influence the flows of foreigners. Accordingly, the return on the technology-intensive Nasdaq Composite Index is included as a potential determinant of flows, along with the Philadelphia Semiconductor Index, which includes the stock prices of around 16 semiconductor stocks traded in US markets and is closely watched in some Asian markets.[11]
The basic empirical model regresses the net purchases of foreign investors (as a percentage of total market capitalisation) in market i (fi,t) upon lagged net inflows, contemporaneous own-market (or domestic) returns (ri,t), and also on various lagged returns series (xt):
Returns are measured as the daily, log-differenced change in the relevant price index. The lag length is set at five, based on preliminary regressions and tests (discussed below) using the final full VAR systems.[12]
Contemporaneous domestic returns are included for the following reason. As is seen in Table 2, contemporaneous flows and returns are strongly correlated in every market. But returns in each domestic market on day t are strongly influenced by the prior overnight (day t−1) US return. If the day t domestic return is not included in the flows equation, there is a risk that day t−1 US returns will be found to be a significant explanator of flows, but that this might be spurious because it is picking up the omitted day t correlation between flows and domestic returns. To avoid the possibility of any such spurious correlation, but without any implications for causation, contemporaneous returns are included as a control variable in the flows equation.
The process of model selection based on Equation (1) is summarised in Table 4. For reference, the top panel first provides the adjusted R2 from equations with only lagged flows, and lagged flows plus contemporaneous domestic returns. The middle panel then presents the adjusted R2 for the equations that separately include five lags of each of the return variables, and the p-values for the hypothesis that the particular return series can be excluded. The bottom panel shows the results of testing for the statistical significance of additional returns series, after controlling for the correlation with the returns series that was the most significant series in the middle panel. The results suggest that domestic returns influence flows in five of the six markets.[13] However, in four of the six cases, foreign returns are also significant explanators of flows, in some cases providing a very dramatic increase in explanatory power compared with equations including only domestic returns. In three of the four cases, the most significant foreign return is a US technology index. Overall, the regressions summarised in this table suggest that the high-frequency net purchases of foreign investors can be surprisingly well explained by just a few variables: the regressions including lagged domestic and foreign returns variables show a median adjusted R2 of 0.38. The substantial explanatory power of these equations stands in contrast to the finding of Brennan and Cao (1997) that equations for quarterly flows (of US investors) could explain only a small proportion of the variance.
| JSX | KSE | Kosdaq | PSE | SET | TWSE | |
|---|---|---|---|---|---|---|
| Adjusted R2 from equations with no lagged returns | ||||||
| With only lagged flows | 0.304 | 0.048 | 0.167 | 0.286 | 0.196 | 0.227 |
| With lagged flows and day t returns | 0.397 | 0.296 | 0.177 | 0.360 | 0.263 | 0.305 |
| Adjusted R2 from adding lagged returns series (with p-value in parentheses) | ||||||
| Domestic returns | 0.410 (0.000) | 0.295 (0.657) | 0.228 (0.000) | 0.369 (0.007) | 0.377 (0.000) | 0.335 (0.000) |
| S&P 500 returns | 0.399 (0.205) | 0.334 (0.000) | 0.205 (0.000) | 0.357 (0.969) | 0.284 (0.000) | 0.426 (0.000) |
| Nasdaq return | 0.396 (0.743) | 0.342 (0.000) | 0.212 (0.000) | 0.357 (0.971) | 0.282 (0.000) | 0.465 (0.000) |
| Philadelphia Semiconductor index return | 0.397 (0.416) | 0.357 (0.000) | 0.211 (0.000) | 0.358 (0.828) | 0.280 (0.000) | 0.454 (0.000) |
| MSCI world index return | 0.397 (0.388) | 0.330 (0.000) | 0.210 (0.000) | 0.359 (0.628) | 0.290 (0.000) | 0.430 (0.000) |
| MSCI emerging markets return | 0.401 (0.106) | 0.307 (0.000) | 0.217 (0.000) | 0.364 (0.099) | 0.281 (0.000) | 0.380 (0.000) |
| Adjusted R2 from equation including the most significant lagged returns series from the middle panel, then adding additional lagged return series (with p-value in parentheses) | ||||||
| Domestic returns | na … |
0.359 (0.139) | na … |
na … |
na … |
0.480 (0.000) |
| S&P 500 returns | 0.409 (0.599) | 0.366 (0.003) | 0.246 (0.000) | 0.365 (0.989) | 0.396 (0.000) | 0.464 (0.669) |
| Nasdaq return | 0.407 (0.943) | 0.357 (0.417) | 0.253 (0.000) | 0.366 (0.900) | 0.396 (0.000) | na … |
| Philadelphia Semiconductor index return | 0.408 (0.700) | na … |
0.253 (0.000) | 0.366 (0.890) | 0.394 (0.000) | 0.475 (0.001) |
| MSCI world index return | 0.408 (0.783) | 0.367 (0.003) | 0.250 (0.000) | 0.367 (0.778) | 0.398 (0.000) | 0.468 (0.076) |
| MSCI emerging markets return | 0.410 (0.312) | 0.364 (0.011) | 0.242 (0.001) | 0.370 (0.194) | 0.376 (0.582) | 0.473 (0.003) |
| Number of observations | 880 | 882 | 882 | 851 | 886 | 879 |
|
Notes: This table shows the results of regressions to determine the variables that best explain the daily net inflows of foreign investors (expressed as a per cent of the previous day's market capitalisation) in the six equity markets over 1999–2002. The top panel shows the adjusted R2 from a regression with only a constant and five lags of net inflows, and an equation that also includes the contemporaneous return in the market. The middle panel shows the adjusted R2 from separately adding five lags of the returns series. The p-values are for the hypothesis that the particular lagged returns series can be excluded. The bottom panel shows the adjusted R2 for equations that include the most significant lagged returns series from the middle panel, and also separately includes five lags of the other returns series. The p-values in this panel test the hypothesis that these additional returns series do not add explanatory power relative to an equation including the most significant return series from the middle panel. |
||||||
The evidence that foreign inflows can be quite well explained by simple regressions such as these can be viewed as evidence that foreign investors tend to respond in a similar way to price movements or the information that drives those movements. This similarity in trading patterns could be interpreted as a form of herding by those investors, even if it is unconscious. It suggests therefore that evidence of herding by foreign investors in other work might be at least partly due to a common response to price movements or other types of ‘fundamental’ information, rather than any deliberate attempt to trade in similar ways to other foreign investors.
Another important point from the regressions is that in almost every case the sum of the coefficients on lagged returns is positive, indicating that higher returns lead to higher inflows. The significance of some of the individual coefficients is striking (detailed results for the VARs are available from the author). For example, the overnight return on US equities has a t-statistic of over 5 for the Kosdaq, KSE, and Thai markets, and over 15 in the case of the TWSE. And the first lag of domestic returns is often also highly significant, with t-statistics of over 12 for Thailand, and averaging around 5 for the JSX, Kosdaq and TWSE.
3.3 VAR Analysis of the Effect of Returns on Inflows
Based on the results in Table 4, results are now presented from VAR equations for flows and returns. VARs have been used by Froot et al (2001), Karolyi (2002), Dahlquist and Robertsson (2004), and others to examine the correlation between inflows and returns in other contexts. The results presented here go beyond the bivariate VARs used in Froot et al with flows and domestic returns. In particular, the analysis also includes US returns, since the above results for four of the six markets would suggest the inclusion of US returns as a determinant of flows. There is a strong case for including US returns in the domestic returns equation, where they may also have an indirect effect on flows.
In setting up the VAR, the considerations discussed above suggest treating the global trading day as notionally beginning with day t−1 US (and European) trading, and then continuing into day t Asian trading. Hence, the VAR that is estimated is as follows:
where:
and rus,t−1 is the relevant US return on day t−1, fi,t is the net purchases (or flows) of foreigners in market i on day t, and ri,t is the return on market i on day t.
The Akaike and Schwartz-Bayes criteria were used to investigate the appropriate lag length. The former suggests lag lengths of two (TWSE, JCI), three (KSE, SET), four (Kosdaq), or five (PSE), whereas the latter suggests a lag length of one in every case. Since degrees of freedom are not a constraint, a common lag length of five lags was adopted for all six markets. This lag length is far shorter than the 40 lags used by Froot et al. However the shorter lags found here are consistent with the work of Griffin, Nardari and Stulz (2003) and would seem plausible given that the decay in autocorrelations in flows is fairly rapid and smooth, and that market efficiency (if it holds) would suggest that returns should respond immediately to innovations in flows.
With only five lags on each variable, the degrees-of-freedom concerns that may have prompted Froot et al to restrict parameters to be equal across all countries are not relevant. Accordingly, given the earlier clear evidence for different empirical models for different markets, empirical models are estimated for each market separately. For the two Korean markets, the Philadelphia Semiconductor Index is the most significant foreign returns series and is included as the US index, while the Nasdaq index is included for Taiwan. For the Thai market there is little to distinguish between several foreign indices, so a broad US index, the S&P 500, is included; the S&P 500 return is also included for Indonesia and the Philippines. To conserve space, the estimated equations for the VARs are not shown, but are available on request.
The impulse response analysis and variance decompositions presented below use the Choleski decomposition or ‘identification by ordering’ to define the channels of contemporaneous causality. Returns in the US market on day t−1 are assumed to be able to affect both day t net flows and day t returns in the markets studied in this paper, with no reverse effect. This assumption makes sense from strict temporal considerations (and the more general observation that most global price determination seems to originate in US markets rather than in these Asian emerging markets). Within the domestic market, the contemporaneous causality is assumed to run from net inflows to prices, but not vice versa within the same day. This assumption is standard in the empirical literature using actual trade-by-trade data, starting with Hasbrouck (1991), and it is also the same assumption made in the papers cited earlier in this section.
The first impulse responses studied are the response of net inflows to innovations in returns. The impacts of one percentage point innovations in US and domestic returns are shown in Figures 1 and 2 over a 20-day period. The scale corresponds to the cumulative net inflows in basis points (i.e., hundredths of a percentage point) of market capitalisation that would result from a one percentage point innovation in returns. In five out of six markets, the cumulative response of net inflows to an innovation in US returns is positive and significant, and in the sixth case (the Philippines) the point estimate is also positive, though insignificant. Hence US returns have a significant effect on flows into emerging markets, even in one case (Indonesia) where they did not appear to have a significant direct effect in the flows equation.
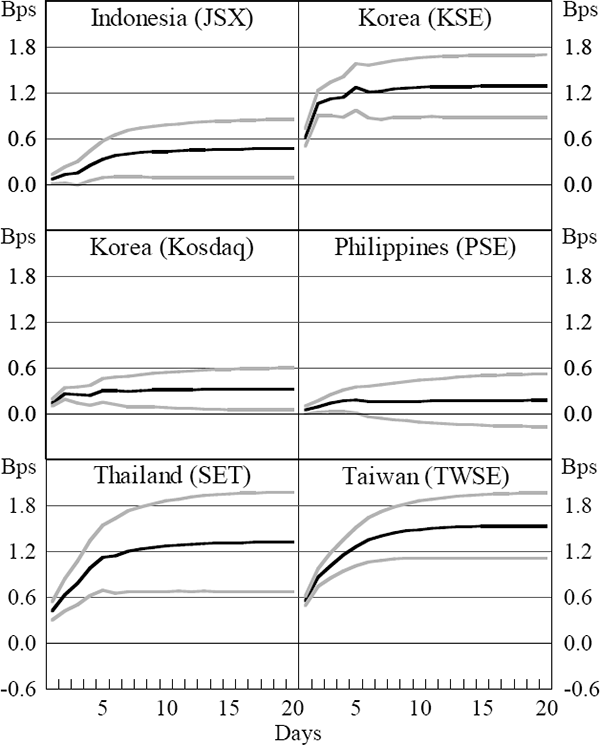
Notes: This figure shows the cumulative response of net inflows (in basis points of market capitalisation) to an innovation of one percentage point in US equity returns. The estimates are obtained from 3-variable VAR systems, which are described in Section 3.3 and estimated using daily data over 1999–2002. The grey lines are 90 per cent confidence intervals based on asymptotic standard errors.
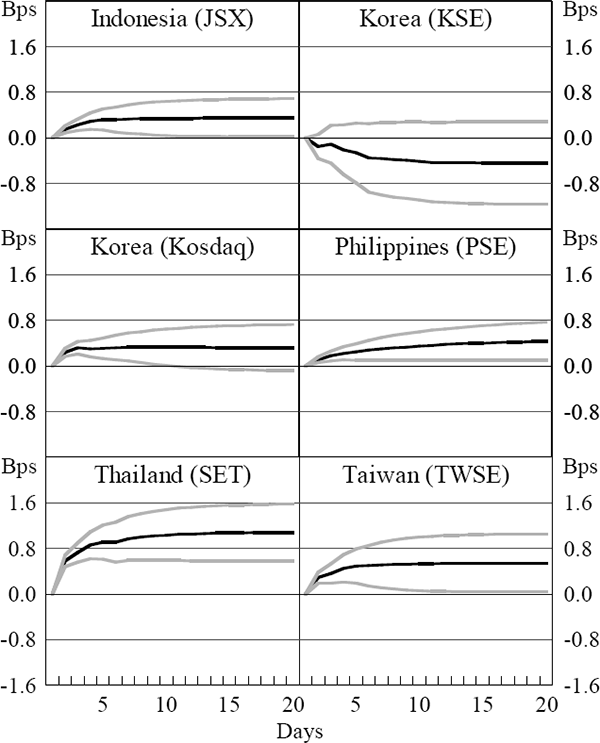
Notes: This figure shows the cumulative response of net inflows (in basis points of market capitalisation) to an innovation of one percentage point in domestic equity returns. The estimates are obtained from 3-variable VAR systems, which are described in Section 3.3 and estimated using daily data over 1999–2002. The grey lines are 90 per cent confidence intervals based on asymptotic standard errors.
The response of net inflows to an innovation in domestic returns is positive and significant in four of the six cases. The exceptions are the two Korean markets. In the case of the Kosdaq, the response is positive but only borderline significant, while the response in flows into the KSE is negative, although insignificant. The results also suggest that innovations to US returns typically have larger effects than equivalent innovations in domestic returns. The median effect of a one percentage point innovation in US returns is a cumulative increase in inflows equivalent to 0.88 basis points of market capitalisation, versus a median effect of 0.39 basis points of market capitalisation for a similar innovation in domestic returns.
An alternative way to assess the relative impact of domestic and foreign returns is via variance decompositions of the VAR systems. In results available upon request, the proportion of the variance in net inflows that is explained after 20 days by earlier innovations in the three variables in the VAR system is examined. Not surprisingly, most of the variance in net inflows is due to lagged own innovations. However, the remaining variance in flows can be decomposed to see whether domestic or US returns are more important. In three cases (Indonesia, the Philippines and Thailand), domestic returns are more important than foreign returns. For the three other markets, foreign returns appear more important, dramatically so in the case of the KSE and the Taiwanese market. Taking the median for the six markets, foreign returns account for about 6.1 per cent of the variance in net inflows, nearly twice as much as the 3.3 per cent figure for domestic returns.
Based on these estimates, one might conclude that conditions in mature markets (push factors) on average affect flows more than conditions in domestic markets (pull factors), at least so far as these can be captured by returns variables. The influence of foreign returns is via two channels: via direct effects on flows, and indirectly via their effect on domestic returns which then affect flows. The relationship between inflows and prior US returns is reminiscent of the argument by Calvo, Leiderman and Reinhart (1993) and others that flows to emerging markets are substantially driven by conditions in mature markets. However, the current finding is somewhat different to the channel proposed by Calvo et al in which flows to emerging markets were driven by low interest rates in mature market countries.
3.4 The Trading Behaviour of Domestic Investors
Of course, foreigners are not the only participants in these equity markets, and if foreigners typically are buyers in particular circumstances then it follows that domestic investors in aggregate must be sellers in response to the same circumstances. In this section, there is an examination of the four markets (the KSE, Kosdaq, TWSE and SET) where there are data on the trading of subgroups of domestic investors, to see if the different types of domestic investors behave similarly, or if there is one particular group that tends to be on the other side of the trades involving foreign investors. For simplicity, the focus is on individual investors and institutional investors (defined as all other domestic investors) rather than on more detailed categorisations where they are available.
Figure 3 presents a summary of the impulse response functions from VARs similar to those estimated in Section 3.3, except that the net purchases of foreigners are replaced separately by the net purchases of domestic individuals and institutions. To conserve space, only the median estimate for the four markets is shown, along with confidence intervals based on the median standard errors. In the case of the response of net purchases to US returns, the top panel suggests little response from domestic institutions. By contrast, domestic individuals tend to be net sellers following positive shocks to US returns, with three out of the four markets showing a strongly statistically significant response. The pattern and magnitude of this cumulative impulse response is reasonably close to the opposite of the response of foreigners. In the case of innovations in domestic returns, the evidence is less clear. In the first few days following the shock to domestic returns, the median response suggests that individuals are net sellers and institutions are net buyers, but over a longer horizon the cumulative flows of both groups tend to be negative, albeit not always statistically significantly so.
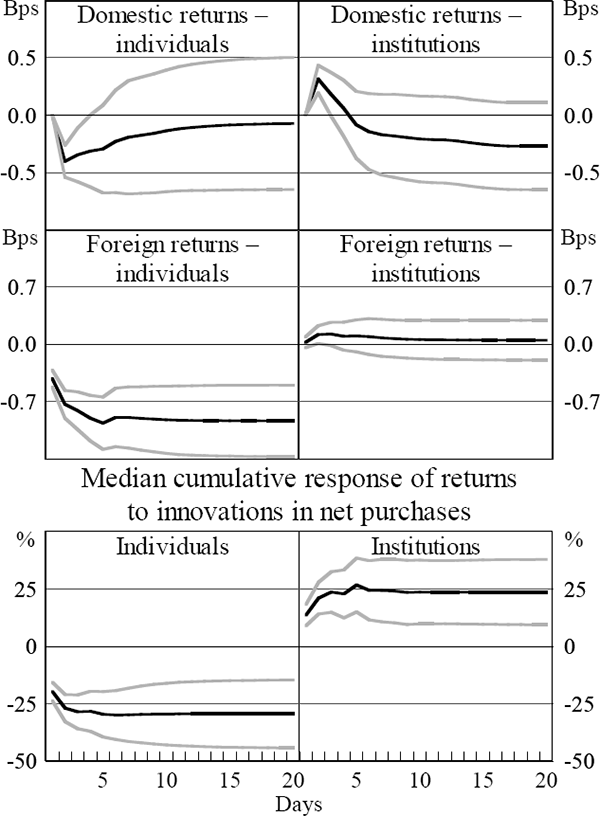
Notes: This figure shows the cumulative impulse responses for 3-variable VAR systems, which are described further in Sections 3.3, 3.4 and 4.4, and estimated using daily data over 1999–2002. The variables in the VARs are the prior overnight return in the US market, net purchases of either domestic individuals or domestic institutions, and the return on the domestic market. The top panel shows the cumulative response of net purchases (in basis points of market capitalisation) of the two investor groups to innovations of one percentage point in US and domestic equity returns. The bottom panel shows the cumulative response of domestic returns to innovations in net purchases equivalent to 1 per cent of market capitalisation. To conserve space, the panels show the median responses for four markets (the KSE, Kosdaq Stock Market, SET and TWSE). The grey lines are 90 per cent confidence intervals based on the median value of the asymptotic standard errors.
These results suggest that it is individual investors who as a group tend to be more often on the other side of the trading of foreign investors. This is not surprising given the adding-up constraint and the fact that individual investors account for the largest share of trading in all markets. In every case where the cumulative response of individuals' flows is significant, the coefficient is negative, indicating that their trading pattern can be characterised as contrarian with respect to recent returns. The results for institutional investors are less clear, and indeed the VAR equations for their net purchases show a substantially lower degree of explanatory power than for the other two groups. This may reflect the more heterogeneous nature of this group, which includes both institutions such as dealers trading on their own behalf, and others such as investment trusts (equivalent to mutual funds) whose trading flows may largely reflect the investment decisions of individuals.
The results above for foreign and domestic investors appear reasonably consistent with research into other markets. For example, Grinblatt and Keloharju (2000) find that foreign investors and sophisticated domestic institutional investors tend to be momentum investors in the Finnish market, whereas households and less sophisticated institutions tend to be contrarians. For Australia, Jackson (2003) has shown that individual investor flows demonstrate negative feedback trading with respect to recent returns. And in the US market, Griffin, Harris and Topaloglu (2003) have found that institutions tend to be net buyers of Nasdaq stocks that rose the previous day and that individuals tend to be net sellers of these stocks.
3.5 Why Are Foreign Investors Positive-feedback Traders?
The findings above raise the question of why foreign investors in these markets are positive-feedback investors with respect to domestic and foreign returns. One possibility is that it is largely a microstructure effect related to differences in order submission strategies. It is indeed possible to imagine a model where the positive-feedback trading of foreigners with respect to foreign returns was entirely unconscious and a product of the order submission strategies of households.[14] However, it seems unlikely that all the observed positive-feedback trading of foreigners is unconscious, and Linnainmaa (2003) concludes in related work using Finnish data that the momentum trading of foreigners and institutions in Finland is indeed ‘intended’. In addition, such unintended order-submission effects could not explain why foreigners appear to be positive-feedback traders with respect to the previous day's return in the domestic market.
A second possible explanation for the feedback trading with respect to foreign returns would be the portfolio rebalancing model proposed by Griffin, Nardari and Stulz (2003). The stylised model of those authors assumes that the stock markets of the home (mature) market and host (emerging) market are uncorrelated, so that shocks to returns in mature markets are shocks relative to the emerging market, and change the portfolio weights of both foreign and domestic investors. These changes in portfolio shares (plus the assumption of home bias) bring forth portfolio flows following price changes in mature markets. However, in reality, prices in virtually all emerging markets appear to move immediately following price shocks in major mature markets, with some responding approximately one-for-one. This would imply that on average there is no change in investors' portfolio weights, so it would be hard to see how a portfolio rebalancing model can explain the response of flows to foreign returns.[15] More generally, the type of calculated portfolio rebalancing implicit in the Griffin, Nardari and Stulz model seems more likely to occur in annual portfolio reviews rather than on a day-by-day basis. This is especially likely given that much investment in emerging markets is via mandates to managers that only invest in these markets, and in these instances it is unrealistic that funds could be shifted so quickly from a manager with a US or mature markets mandate to a specialist emerging markets manager.
It is also noteworthy that in those cases where foreign returns are significant explanators of flows, the most significant foreign returns – by a very strong margin in the two largest markets – are often technology-based indices rather than the broad indices that might be most relevant to the wealth of foreign investors. Given that the Taiwanese market and two Korean markets are heavily weighted in technology stocks (and their broader economies are dependent on the technology cycle) the significance of the US technology indices seems more consistent with a third explanation for the positive-feedback trading of foreigners, namely a story of extraction of information about fundamentals. An information extraction or extrapolative expectations explanation is presumably also the prime candidate for explaining the importance of lagged domestic returns in explaining the inflows of foreigners. Information asymmetry models (e.g., Brennan and Cao 1997) would suggest foreigners might rationally derive information about future domestic returns from lagged returns. Whether this is entirely rational or based more on sentiment is, of course, impossible to assess. Indeed, the line between a rational information-extraction or extrapolative expectations explanation and a behavioural or sentiment model is presumably a fine one, and some authors (e.g., Brown et al 2003) have suggested that investor flow variables can be viewed as measures of investor sentiment.
Footnotes
These indices are also the ‘headline’ indices used in newswire stories reporting the performance of each market, and are available to investors on a real-time basis, unlike some of the (narrower) indices provided by international providers such as MSCI and S&P/IFC. The analysis uses domestic currency returns, but the results are little changed using US dollar returns. [8]
For example, although it may under-represent global fund managers, the sample of emerging market equities used by Borensztein and Gelos (2003) included $71 billion of assets managed by dedicated emerging markets managers at end 2000, versus only $12 billion by non-dedicated managers. [9]
As of late 2002, the weights of these two companies in their national indices were 18 and 20 per cent, respectively. The total weight of the technology sector in the Taiwan and Kosdaq markets was around 60 per cent. [10]
These technology-related indices were the only industry returns investigated; the strong significance of these indices is not the out-turn of a larger search using other industry series. The inclusion of these indices seems easily justified based either on the importance of computer-related sectors for several markets in Asia, or the observation that the defining industry effect in global equity over 1999–2002 was the Nasdaq/technology effect. It is noteworthy that the stocks in the Philadelphia Semiconductor Index represent a very small proportion of the total US market, so the finding that this index is often substantially more significant in regressions than the S&P 500 index is strongly suggestive of its significance being due to its industry-level information rather than to it being a proxy for overall US equity returns. [11]
The use of daily data with five lags means that market-specific holidays would result in the loss of many observations due to missing values. Rather than assuming unchanged price levels when markets are closed, I deal with the problem as follows. I omit any day when there is no trading in the market that is the subject of the regression and calculate the price change from the last time the market was open. I also omit any observation when the US market was closed on day t−1 and aggregate the daily net inflows in cases where the domestic market has traded while the US market was closed. Thus, each observation in the VARs corresponds to the minimum period necessary to get synchronised close-to-close data for both the US and domestic market. [12]
The exception is the KSE, where domestic returns are not significant when added to a regression for total (physical and futures) net purchases that already includes foreign returns: this finding reflects a positive significant impact of domestic returns on physical market inflows being offset by a negative impact on futures market net purchases. [13]
Suppose that each morning, one group of investors (i.e., foreigners) assessed the implications of overnight US returns for domestic prices, and stood ready to buy (sell) at prices just below (above) the new equilibrium price. If another group of traders (i.e., individuals) placed only limit orders and did not actively monitor them, we would see the first group transacting with the second group whenever there were overnight US price changes that implied an increase in domestic stock prices and thereby activated the limit orders of the second group. In this case, the first (second) group would appear to behave as positive-feedback (contrarian) traders with respect to returns in other markets, although in neither case would this really be a conscious strategy. The result would be that foreigners' flows into these markets would represent part of the adjustment of domestic prices to global equity market developments. This is perhaps consistent with the finding of Evans and Lyons (2003) that order flow in the foreign exchange market represents part of the process of price adjustment following macroeconomic news. [14]
Indeed, in regressions available upon request, I estimate a simple regression for each of the six Asian markets which suggests that returns in four markets (the KSE, Kosdaq, TWSE and SET) typically moved about one-for-one (or more) with movements in mature markets in this sample period. By contrast, the two other markets (Indonesia and the Philippines) moved less than one-for-one. A portfolio rebalancing model would predict that increases in foreign returns should lead to net inflows into the latter group of markets, but should not lead to inflows into the first four markets. However, this is broadly the opposite of what is observed in Figure 1 and Table 4. [15]