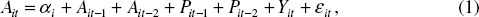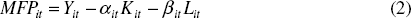RDP 2003-10: Productivity and Inflation 4. Methodology and Data
September 2003
- Download the Paper 224KB
The correlation apparent in the relationship between Australian aggregate inflation and productivity growth in Table 1 can be tested econometrically, using annual data. It is marginally statistically significant – as mentioned in the introduction. This may be for many reasons but two are most important: 1) we only have 36 annual observations representing one ‘cycle’ in the productivity-inflation relationship, so statistical significance is difficult to achieve; and 2) the aggregate data may mask divergent industry-level relationships. By estimating each industry separately we are not forcing all the coefficients to be the same and can reveal if there are significant differences between industries.[10] The Seemingly Unrelated Regression (SUR) estimation technique applied to industry level data offers the possibility of ameliorating some of these problems. While we will have the same length of data for each individual industry, the SUR method is potentially more efficient because it uses cross-equation information.
4.1 Model
Following previous practice and the insights from the literature we look at Granger-causality regressions with an output gap to control for the business cycle. Thus the basic regression estimated (explaining causation from the IPDs to productivity growth) is:
where Ait is productivity growth, Pit is the change in the implicit price deflators (IPDs), and Yit is the output gap, all for industry i in year t. We look at both labour and multifactor productivity (MFP) to shed light on the effect of inflation on capital accumulation. The data seem most comfortable with the inclusion of two lags; two lags also has the advantage of minimising the loss of degrees of freedom.
Some of the theories discussed suggest that inflation slows the optimal accumulation of capital. If that is the major channel transmitting inflation's effects into productivity growth, we would expect to see a relationship between inflation and labour productivity but not between inflation and multifactor productivity (which takes account of capital accumulation) – this explanation does not hold, as Section 5 reveals. We explore this angle more fully in Section 7.
4.2 Data[11]
Australian data are more problematic than those available for the G7 studies we are trying to replicate. Unlike the series dating from WWII available to other studies, the Australian data needed to calculate productivity measures become complete only in 1966, and even this run is subject to discontinuities.
We begin with the non-farm market-sector ANZSIC (Australia New Zealand Standard Industry Classification) industries. Finance and insurance is excluded because the necessary data only begin in 1986, which would severely limit our available observations. The remaining industries were not seriously affected by the transition from ASIC (Australian Standard Industry Classification) to ANZSIC,[12] and all have output that is relatively easy to measure.[13] For each of these industries we constructed measures of prices, and multifactor and labour productivity, plus a measure of the business cycle specific to that industry. Appendix A shows the price and productivity variables by industry.
Our price variables are the industry gross-value-added (GVA) implicit price deflators (IPDs). These are relatively straightforward to calculate, being an index created by dividing each industry's nominal GVA by its real GVA. As these are measures based on value added they can be affected by changes in input prices as well as output prices. Nonetheless, the IPDs represent the specific price environment an industry faces in the course of its business.[14]
Labour productivity is also a relatively clean calculation – in particular, it is free of capital measurement issues. We calculate it by dividing an industry's real GVA with the total number of hours worked in that industry. Total hours were calculated by multiplying the year-to-August average weekly number of hours worked (for both full- and part-time employees, that includes, in particular, overtime and strikes) by the year-to-August average total number of people employed in that industry.[15]
More complex is multifactor productivity. Here we followed a standard Solow growth accounting framework, which treats productivity growth as the residual of output growth after growth of labour and capital input are accounted for. Thus:
where all terms are expressed in year t for industry i as annual percentage changes, Y is industry i's real GVA, α and β are the factor share of income attributable to capital and labour respectively, L is labour input, and K is capital input. The income shares were calculated by dividing an unpublished ABS series of industry-level capital rental on the productive capital stock[16] with industry nominal GVA. Labour's share of income is the complement of capital's share.[17] The capital input measure comes from the ABS's experimental ‘capital services’ index, which accounts for productive capacity of capital, making it more appealing than the standard capital stock measure. Labour input is the total hours worked series calculated for the labour productivity measure.
To absorb the business cycle component of our data, we need a measure of each industry's output gap. We generate this by subtracting a Hodrick-Prescott filter generated trend of logged industry GVA growth from the same output measure.[18] These gaps are plotted in Figure B1. For reference, they are plotted against an aggregate non-farm output gap series (generated in Gruen, Robinson and Stone (2002)). While there is discussion in the literature about whether the HP filter is the most appropriate output gap measure, it is the most feasible one in our case. It also manages to control for the regular feature that productivity is higher in booms and lower in recessions due to problems with the measurement of work intensity. Further, when we augmented our model with other business cycle measures, they were not significant.[19]
For completeness, we must mention some caveats about our data. These caveats are typical of any study using longer-term Australian macroeconomic data. As there is no consistent measure of nominal or real GVA from 1966 to 2002 both GVA series had to be generated. The shift from SNA68 to SNA93 in the early 1990s is the most important break; the change from ASIC to ANZSIC around the same time is far less important. To overcome this break, we use the full length of the latest dataset and splice the early series onto years prior to 1975 for real GVA and 1989 for nominal GVA.[20] Likewise, some of our later series combine disaggregated series. We simply aggregate additively or by using a weighted average of the two sub-series where appropriate.
The second caveat is that any series generated from gross-value-added suffers issues related to the inclusion of taxes and subsidies. In calculating GVA, the ABS currently excludes taxes and subsidies on output but includes the taxes and subsidies in production; however, the rental estimates include taxes and subsidies on output. This is inconsistent, but not fatally so given the length of our study (Simon and Wardrop 2002).
4.3 Stationarity
A critique made of earlier studies correlating productivity growth with inflation is that the two series are of different orders of integration. Specifically, these papers argue that inflation is I(1), whereas productivity growth is stationary. Here we check our series using Augmented Dickey-Fuller (ADF) tests. Table 3 indicates that non-stationarity would not seem to be a problem for our study.
| IPDs | Labour productivity | MFP | |
|---|---|---|---|
| Mining | Yes** | Yes** | Yes** |
| Manufacturing | Yes** | Yes** | Yes** |
| Utilities | Yes** | Yes** | Yes** |
| Construction | Yes** | Yes** | Yes** |
| Wholesale & retail trade | No | Yes** | Yes** |
| Transport, storage & communications | No | Yes** | Yes** |
|
Note: ** indicate the result's significance at the 5 per cent levels. |
|||
We see that only for wholesale & retail trade and transport, storage & communications do we fail to reject that the IPD is I(1). A range of factors lead us to treat all series as I(0): the weight of evidence from the other industries; our economic priors (that inflation is I(0), potentially with breaks); the tendency of the ADF test to under-reject the null hypothesis; and, our caution regarding the series for the transport, storage & communications industry group (discussed in Section 5).
Footnotes
For example, each industry will probably have a different correlation with the aggregate business cycle. [10]
Through the course of this study we introduce other variables to test the robustness of our model and to explore the transmission mechanism between inflation and productivity growth. We discuss these series as they appear. [11]
To ensure we had enough observations, some ‘industries’ had to be re-aggregated after the ABS (Australian Bureau of Statistics) disaggregated them – for example – transport & storage from communications when it shifted from ASIC to ANZSIC. [12]
These industry sectors are mining, manufacturing, electricity gas & water (‘utilities’), construction, wholesale & retail trade, and transport, storage & communications. Although several of these series are available in a less aggregated form from the early 1980s (transport & storage separates from communications, as does wholesale from retail trade later), maximising our number of observations is important and given the SUR model does not adjust for unbalanced data, we keep these series aggregated through our full sample. [13]
We examine the correlation between industry and these aggregate price measures and what this might suggest in Section 5.2. [14]
Both these series are sourced from the ABS's Labour Force Survey. The ABS recommends use of this source over the alternatives, at least for total employment (ABS Cat No 6248.0). [15]
We are grateful to the Capital, Production and Deflators section of the ABS for providing these data. [16]
The calculated capital shares are highly plausible. For example, mining has a high capital share of income (66 per cent on average for 1965–2002) while construction has a low capital share (1965–2002 average of 19 per cent). [17]
We set the smoothing parameter to 100, as is standard practice for an annual series. We reduced the end-point problem at the start of our series by applying the HP filter to industry GVA from 1965, while the data analysed starts in 1967. [18]
Discussed in Section 6.2. [19]
There are two years of overlap between the new and old real GVA series. So, in splicing the series together, we used the average ratio of the two series across these two years. [20]