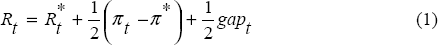RDP 2002-05: Real-Time National Accounts Data 1. Introduction

For analysts of macroeconomic trends and prospects, quarterly national accounts data are amongst the most important and eagerly awaited economic information available. Recent quarterly growth figures are regarded as a key summary indicator of the current state of the economy. Moreover, they are an essential ingredient in estimation of the output gap, or current level of actual output relative to a theoretically assessed potential level. This gap represents an important indicator of the extent of excess (or insufficient) demand within the economy – with implications for future inflation and for the optimal trajectory of monetary policy.

Like many economic statistics, however, official estimates of quarterly output are subject to uncertainty and subsequent revision, as further data come to hand and a more detailed reconciliation of different component indicators or survey measures becomes possible. It is therefore important to appreciate that the ‘true’ values for the national accounts data can never be known precisely. The official estimates of these quantities may, in practice, be an inaccurate guide to the ‘true’ state of the economy, not just initially but even for some time after the event.

The critical question is: how significant is this problem of initial mismeasurement and subsequent revision of national accounts data, both in scale and persistence? We shall refer to this issue henceforth as the ‘real-time problem’ for actual output data, reflecting as it does the difficulty which confronts analysts of having to reach judgements based only on the information available in real time, rather than with the benefit of hindsight.

The next two sub-sections offer further background on two principal aspects of the ‘real-time problem’, while the structure of the remainder of the paper is set out in Section 1.3.

1.1 Output Growth Estimates as a Real-time Economic Indicator

Given the importance attached to quarterly national accounts releases, and the widespread use of such data, it is perhaps surprising how little attention seems to be paid to the fact that these data are subject to (sometimes substantial) revision. While most commentators are undoubtedly aware that alterations are made to such data, few attempts seem to have been made to analyse methodically the scale or pattern (if any) of these adjustments. Likewise, little work seems to have been done on either the implications of possible future changes for how we should interpret the data in the most recent accounts, or the implications of the alterations to historical data incorporated in these accounts for forecasting models estimated on these historical data.

Within the Reserve Bank of Australia (RBA) a notable exception to this was the paper by Gray (1983) on ‘Revisions to National Accounts’. In this paper he analysed, inter alia, the average scale of revisions to several main national accounts aggregates, the persistence of initial mismeasurement of these aggregates, and the relative degree to which the quarterly, semi-annual and annual growth rates of these aggregates tended to be affected by revisions. In addition, he extended his analysis to a selection of 10 of the major components of the income and expenditure sides of the accounts, and discussed the chief sources of revisions to both component and aggregate series.

A further exception to the general tendency to neglect revisions was the paper by Rossiter and Brown (1989) from the Australian Bureau of Statistics (ABS). In this paper they described preliminary results from modelling of the revisions to various current price, seasonally unadjusted national accounts aggregates (specifically gross domestic product (GDP), gross farm product and private final consumption expenditure). Besides extending previous work on the analysis and modelling of revisions to economic time series, a principal objective of their study was ‘to assist the development of improved methodologies for preparation of the Australian National Accounts (ANA)’. One interesting question flowing from this latter objective is whether such analysis, together with improvements in data collection and reconciliation, may have resulted in a gradual decline in the average degree of uncertainty surrounding estimates of GDP growth. We return to this issue later in this paper.

1.2 Output Gaps and Policy Rules in Real Time – The US Debate

A second reason for the importance of real-time issues for monetary policy-makers stems from the periodic revival of interest in the debate between rules-based and discretionary monetary policy, coupled with the fact that various well-known monetary policy rules base their recommended level of the policy instrument on estimates of the output gap.

In recent years this debate has attracted renewed interest, principally sparked by a series of papers by Taylor (1993, 1998) concerning US monetary policy since the 1960s. Taylor's conclusions, however, have been the subject of vigorous debate. This debate has centred around the informational assumptions underpinning his analysis, and the implications of ‘real-time’ informational limitations for both the conduct of monetary policy and the fair counterfactual analysis of such policy.

In his 1998 paper ‘An Historical Analysis of Monetary Policy Rules’, Taylor studied actual Federal Reserve behaviour in setting monetary policy over the previous four decades. He then compared the outcomes achieved for output and inflation over this period with counterfactual simulations in which monetary policy was instead set according to a simple rule, specifically his own well-known ‘Taylor rule’.

Under this rule the policy interest rate is adjusted linearly in response to current deviations of inflation from some specified target level, π^*, and of actual output from an estimated potential level. Specifically, Taylor's rule (with the standard choice of coefficients) is given by:

where R_t denotes the policy interest rate; R_t^* represents the neutral level of R_t (or the sum of the current annual inflation rate, π_t, and the neutral real interest rate, r^*); π^* represents the target annual inflation rate; and gap_t is the output gap in period t.

Taylor's analysis led him to make a striking claim, namely that policy run according to his simple rule would, on average, have produced superior macroeconomic outcomes to those achieved by actual policy over the past 40 years. Having previously observed the similarity between the policy prescription of his simple rule and actual Federal Reserve behaviour in the late 1980s and early 1990s, he observed that:

A comparison of policy rules and economic outcomes points to the rule the Fed has been using in recent years as a better way to run monetary policy than the way it was run in earlier years. (Taylor 1998, p 35)

Moreover, he claimed that for the US both the ‘great inflation’ of the late 1960s and 1970s and the severe recession of the early 1980s, as well as a period of monetary tightness in the early 1960s, reflected deviations of monetary policy from that prescribed by the Taylor rule, and could be classified as ‘policy mistakes’.^[1],^[2]

Taylor's analysis appeared to provide powerful evidence in support of, if not the mechanical adoption of policy rules such as Taylor's rule by central banks, at least an enhanced role for such rules in informing the setting of monetary policy. His results, however, have been criticised, in particular by Orphanides (2000), on the grounds that the informational assumptions underpinning them were unrealistic.

Clearly, the practical operation of a policy rule involving the output gap, such as Taylor's rule, requires the policy-maker to feed in data on both actual and potential current output. Orphanides observed, however, that in Taylor's work the actual output data used were the latest available historical time series, and therefore included all revisions made to each quarter's data since their first release. None of this information on subsequent revisions, however, would have been available at the time to policy-makers setting short-term interest rates, whether by rule or by discretion. In the event that revisions were substantial, this might mean that policy set according to Taylor's rule using ‘real time’ actual output data might be significantly different from that based on the same rule using latest available historical data. To this extent, the improved outcomes found by Taylor under his rule-based policy might not represent the superiority of his rule over actual policy. Rather, they might simply represent the benefit of hindsight, contained in the knowledge both of future economic developments and of revisions to past economic data, in assessing the true state of the economy at critical junctures.

Orphanides's charge of failing to distinguish between real time and latest available historical data in relation to actual output is clearly a serious one. Potentially more important again, however, is the same charge in relation to potential output, which Orphanides suggested may also be levelled against Taylor's analysis.

Orphanides argued that potential output, being unobservable, is particularly prone to prolonged and substantial mis-estimation. Moreover, as a purely theoretical construct, the scope for errors in its real-time estimation is much greater than for the corresponding measurement of actual output. The risk of such mis-estimation would be especially great where a shift occurred in long-term trend productivity growth, since such a trend shift would likely be difficult for policy-makers to detect for many years, obscured as it would be by cyclical variations and statistical noise.

Pursuing this point, Orphanides undertook a careful study of Federal Reserve papers over much of the past 40 years, which contained real-time estimates of the output gap, prepared either by the Fed or the Council of Economic Advisers. Drawing upon this, he argued that the estimates of the output gap used in Taylor's work, based as they were upon a recent vintage of historical data, differed dramatically from those which were available in real time. This was especially true over the 1970s, where the trend decline in US productivity growth from the late 1960s onwards was not fully apparent to US policy-makers for nearly a decade.

When Orphanides re-ran Taylor's counterfactual simulations using his real-time data, he found that under this constraint the Taylor rule actually performed slightly worse, on average, than did actual policy over the period 1966 to 1993.^[3]

Taylor (2000) has, in turn, disputed Orphanides' results, arguing in particular that the real-time estimates of potential output used by Orphanides were not accepted by serious economic analysts at the time – especially in those periods where they implied large output gaps which seemed at odds with other indicators of the state of the economy. Nevertheless, in the case of the US data, Orphanides's work served to highlight how substantial this real-time informational issue could be. This may, in turn, have helped to revive interest in the significance of real-time issues for numerous other economic questions, from general macroeconomic forecasting to microeconomic issues such as banking supervision.^[4]

1.3 The Structure of this Paper

Clearly, it is important for analysts to be aware of the scale, frequency, persistence and pattern (if any) of uncertainty surrounding the estimates of national accounts aggregates released each quarter by the ABS – and of the implications of this uncertainty for real-time estimates of the output gap. This paper should be viewed as the first of two addressing these general issues for the case of Australia.

A companion paper (Gruen et al 2002) addresses the problem of constructing real-time potential output estimates, and in so doing attempts to analyse whether, for Australia, Orphanides's real-time critique need be truly fatal to the use of output-gap estimates as a guide to the setting of monetary policy. In this paper, however, we confine our attention to a purely descriptive examination of the likely scale of the real-time issue for Australia, focusing just on actual output data.

In Section 2 we begin by outlining the availability of real-time actual output data for Australia. Section 2.1 provides a brief run-down of the data we have obtained for various alternative broad measures of output, while Section 2.2 provides a historical rationale for our choice of two real-time actual output measures upon which to focus in the remainder of the paper.^[5]

The main content of this paper is then presented in Section 3, where we undertake a basic inspection of the scale of changes over time to our chosen measures of actual output. This is done to provide a feel for the magnitude of the real-time issue facing policy-makers. Purely from such a simple inspection, without any sophisticated model-based analysis, a number of important conclusions can still be drawn regarding the likely seriousness of real-time informational limitations for assessing the current health of the economy.

Footnotes

Other authors, such as Clarida, Gali and Gertler (1998) and Judd and Rudebusch (1998) have drawn similar conclusions, albeit carefully qualified in light of the problem of interpreting counterfactual regression results based on latest available rather than real-time data. [1]

In fairness, in relation to the early 1980s ‘policy mistake’, Taylor (1998, p 39) notes that: ‘it should be emphasised that this period occurred right after the end of the 1970s inflation and the higher interest rates than recommended by the policy rules may have been necessary to keep expectations of inflation from rising and to help establish the credibility of the Fed…In my view this period has less claim to being a ‘policy mistake’ than the other two periods’. [2]

It should be noted, of course, that the importance of an awareness of the implications of informational limitations for monetary policy was not a new insight on Orphanides's part. As he himself pointed out:

As early as 1947, Milton Friedman had sharply criticised reliance on unrealistic informational assumptions for Keynesian prescriptions to maintain ‘full employment’. (Orphanides 2000, p 4) [3]

An illustration of the growing interest in the issue of real-time informational limitations is the establishment by the Federal Reserve Bank of Philadelphia of a quarterly Real Time Data Set for Macroeconomists (RTDSM) – see Croushore and Stark (2000). For an example of the potential importance of real-time issues in microeconomic analyses, see for instance Gunther and Moore (2000), who examine the performance of early warning models used in the monitoring of the financial condition of US banks. [4]

The majority of these raw data were assembled and provided to us by the Analytical Services Branch of the Australian Bureau of Statistics, without whose assistance this project would not have been possible. The data, however, represent unofficial ABS statistics, as they have not been subjected to the usual quality assurance checks which apply to all published ABS releases. While some reconciliation checks against ABS publications have been undertaken, a full consistency check of the data has not been carried out. Responsibility for any data errors rests solely with the authors. The real-time data on the two GDP measures ultimately studied in this paper (GDP(E) and a hybrid measure discussed in more detail in Section 2.2) are available from the authors upon request. [5]