RDP 2001-04: Measuring the Real Exchange Rate: Pitfalls and Practicalities 3. Weighting Choices

The choice of weighting scheme depends on the purpose. For example, import-weighted indices are generally the most appropriate when assessing the effect of exchange rate movements on import prices. But assessing the effect of exchange rate movements on competitiveness more generally is never simple (Rhomberg 1976). In some cases, trade shares might seem a reasonable basis of comparison, but they do not reflect the ‘third-country’ effects; that is, the competition that home-country exports experience in foreign markets from other sources of these exports (see RBA (1998)). Nor do they capture the effect of exchange rate movements on components of the capital account or foreign liabilities. This section examines each of the main candidate weighting schemes, and sets out some of the measurement issues encountered when using them. The data sources for the weights used by the RBA are set out in the appendix.

3.1 Trade, Import and Export Weights

The relative importance of a nation's trading partners seems a natural basis for assessing changes in competitiveness. This is the approach used by the RBA in its published trade-weighted index (TWI) and numerous other published series; for example, those published by the Bank of England, Bank of Canada and JP Morgan; see also Anderson, Karamouzis and Skaperdas (1987). The weights are derived as the share of total trade (exports plus imports) with each country, as measured in balance of payments statistics. In the RBA's TWI, the weights are based on annual data and revised annually in most cases. An alternative approach could be to use weights that change more or less frequently, or that are based on rolling averages of trade shares. The methodology for deriving import or export-based weights is essentially identical.

For some purposes, however, these weighting schemes may be inappropriate, because they only capture the bilateral trade between the home country and its trading partners. This is unlikely to be a good proxy for the importance of those countries in determining world price and demand conditions. To the extent that traded goods are sold on world markets, the composition of the home country's current trading partners is less important, as other trading partners could easily be found. Moreover, bilateral weights do not allow for third-country effects, as already mentioned.

An alternative approach would be to measure countries' shares of world trade, rather than bilateral trade with the home country. This is the approach taken by the FRB Index (Anderson et al 1987). These weights, known as multilateral trade weights, should better capture the importance of other countries in determining the competitive pressures faced by home-country exporters on world markets. On the other hand, this weighting scheme ignores the competitive effects of the importing country's domestic producers, which are implicitly incorporated into measures based on bilateral trade. This scheme also has the major practical disadvantage of enlarging the problem of collecting timely and accurate trade data by including countries that are neither trading partners nor competitors of the home country, and that might not necessarily publish high-quality data.

An extension of the multilateral trade weight approach derives weights from a general equilibrium model of world trade. This is the approach taken by the IMF's MERM exchange rate indices (Artus and McGuirk 1982). Rather than using weights implied by countries' actual trade patterns, these models derive weights that incorporate the estimated responses of trade patterns to movements in exchange rates. This approach explicitly accommodates the determinants of trade flows, namely the price elasticities of countries’ demand for traded goods, and the changes in traded-goods prices induced by the exchange rate movements.

3.2 Third-country Export Weights

As mentioned above, bilateral trade weights of the type used in the RBA TWI do not necessarily capture the changes in the home country's competitiveness relative to alternative suppliers of its exports (RBA 1998). That is, there may be countries with which the home country trades little, but with which it competes intensely for export markets.

In contrast to a standard bilateral trade-weighted or export-weighted index, third-country export-weighted exchange rate indices tend to weight more highly countries with export compositions similar to that of the home country. For example, a third-country export-weighted index for Australia weights countries such as the United States, Canada and Brazil more highly than does the standard TWI. Like multilateral trade weights, however, calculating third-country trade weights could potentially be hampered by the difficulty in obtaining comparable timely data. This is because the calculation then relies on trade statistics published in other countries, whereas bilateral trade weights can be calculated from the home country's trade statistics. The third-country weighted index presented in this paper is a fixed-weight index based on 1994 trade data from the United Nations.

3.3 GDP Weights

One problem with trade weights – even multilateral trade weights – is that they only cover goods and services that are actually traded. This does not necessarily correspond to countries' shares of world production, and hence their influence on world prices. Bilateral trade weights exclude countries with a large influence on world prices, but with which the home country does not trade much. Multilateral (world) trade-share weights overweight small open economies that only trade with a small set of other open economies and thus have little influence on world prices (the smaller EU nations being obvious examples).

For this reason, it is sometimes preferable to use weights based on countries' shares of world GDP. However, calculating GDP on a comparable basis requires conversion to a common currency – usually the US$. This means that, unless some smoothing or other adjustment is applied, the weights in the exchange rate index will be subject to the same fluctuations as the exchange rates they are intended to weight. This is clearly undesirable, as it weights countries against which the home currency has recently depreciated more highly, thereby creating a depreciation bias into the results. One way to avoid this problem is to use purchasing power parities (PPP) to convert the GDP figures. The PPP conversion rates are calculated by the OECD and used by the IMF for the GDP comparisons in its World Economic Outlook publication (IMF 2001); these are the basis for the GDP weights used in this paper. Another way of reducing this bias is by taking a moving average of exchange rates to convert the GDP shares. This is the approach taken in the World Bank Atlas measures of GDP, which are converted using 3-year moving averages of bilateral exchange rates with the US$. Using this method gives fairly similar results to the PPP-based approach.

3.4 Capital Account Weights

The weighting schemes discussed so far focus on nations' trading behaviour. For some purposes, it may be preferable to use weights based on capital market quantities. For example, a trade-weighted index does not capture the effects of exchange rate movements on the domestic-currency value of (unhedged) foreign debt or holdings of foreign equity assets. Therefore, for some purposes, an exchange rate index using weights based on quantities from a country's international investment position will be more appropriate than one based on its trade accounts (Robson and Makin 1997).

There are several issues to be aware of when constructing such an index. Firstly, it should be constructed from information on the currency denomination of the assets and liabilities, not the identity of the counterparty country. For debt assets and liabilities, the currency and counterparty can differ. For example, if Australian investors were borrowing from Japanese investors by issuing US$-denominated securities, this should add to the weight of the US$ in such an exchange rate index, not to that of the yen. For weighting schemes based on the composition of equity assets or liabilities, it is reasonable to assume that the liability-side counterparty corresponds to the currency. That is, Australia's equity liabilities are in A$, while its equity assets are in the currency of the other country.

Secondly, a large proportion of Australia's foreign liabilities – all of the equity liabilities and around 40 per cent of debt liabilities – are denominated in A$. The appropriate treatment of domestic-currency denominated stocks in calculating weights for exchange rate indices is to include them as the weight for an ‘exchange rate’ that never moves relative to the home country currency. If only foreign-currency denominated assets and liabilities are included in its weights, the resulting exchange rate index will be more volatile than the actual valuation effects of exchange rate movements on these asset and liability stocks. Therefore the exchange rate index would over-predict the effects of exchange rate movements on the value of foreign assets and liabilities. Since the usual purpose of an exchange rate index weighted by asset and liability stocks is to help predict valuation effects in those stocks, this over-prediction is clearly undesirable.

Thirdly, under the standard treatment of foreign assets and liabilities, the values of foreign-currency denominated assets and liabilities are recorded separately from any associated hedging through derivative contracts. Therefore calculation of an exchange rate index based on the currency composition of foreign assets and liabilities will be a good predictor of reported valuation effects due to exchange rate movements, but will not properly represent the vulnerability or indebtedness of the home country. This effect cannot be offset using information on derivatives from the balance of payments; these statistics record the market value of the derivative contract, not the notional value hedged, which could be much larger.

In Australia, foreign debt and lending by currency are only available on a comparable basis since 1997; accordingly, it is not currently feasible to use exchange rate indices based on these weighting schemes in econometric work. Figure 3 shows a range of measures of the real exchange rate using weights based on foreign assets and foreign liabilities and debt. Because of the particular composition of Australia's foreign liabilities, the nominal AUD/SRD rate moves in the same direction as exchange rate indices based on capital account and international investment position quantities, and could therefore be used as a proxy. It is more volatile than the debt-weighted index shown in Figure 3 because of the presence of A$-denominated foreign debt. Of course, for reasons described in Section 2, a real AUD/SRD exchange rate index still has to be calculated from the component real bilateral rates.

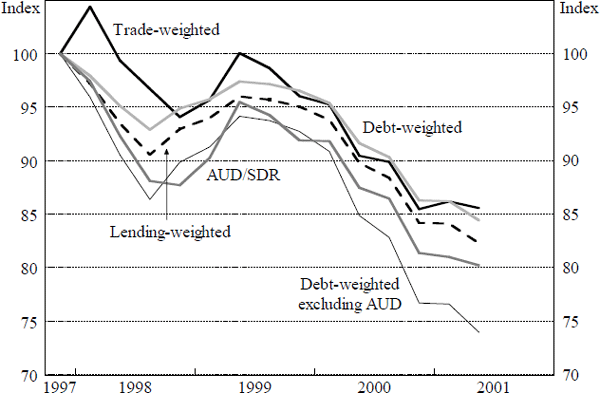
If the weight on the A$ is excluded and the other components rescaled, the debt-weighted exchange rate index displays somewhat greater volatility than the bilateral exchange rate against the SDR (Figure 3). This is due to the greater relative weight of the US$ in this index. A debt or lending-weighted index excluding the A$ shows the effect of exchange rate movements on the foreign-currency denominated component of the relevant parts of Australia's international investment position, but beyond this its economic interpretation is not obvious.