RDP 2001-02: Changes in the Determinants of Inflation in Australia 4. The Inflation Process
May 2001
- Download the Paper 372KB
The 1990s witnessed changes in the behaviour of key explanators of inflation that have been conducive to low inflation. Some of this behaviour has been unusual and some has been indicative of a more structural change. Taken together, have these developments generated a change in the inflation process?
To answer this question, first, we appeal to econometric evidence of structural breaks in a mark-up model of inflation for Australia. We refer to the inflation equation detailed in Beechey et al (2000), in which prices are modelled as a mark-up on import prices and unit labour costs; the mark-up is allowed to vary cyclically with the output gap and is also influenced by oil prices.[34] (The equation has been estimated using an error-correction specification.)
Beechey et al (2000) have examined the stability of this equation, focusing on whether a structural break is evident in the March quarter of 1993, which corresponds to the introduction of the inflation-targeting regime. While their purpose was to test the relevance of the Lucas critique for the model, given the change in articulation of monetary policy objectives, the same break point usefully defines the beginning of the current low inflation episode. They found that a structural change in the inflation process in the post-break period is not indicated by standard Chow-type tests (on the significance of individual dummies or on their joint significance). However, this standard test of structural stability may mask useful details of changes in the way shocks to inflation are propagated.
An alternative insight into possible structural changes in the inflation process can be gleaned by examining the speed with which inflation responds to disequilibrium in the long-run relationship between prices and costs. The error-correction specification of the inflation equation is helpful in this regard because it features a speed of adjustment parameter. We recursively re-estimate the Beechey et al inflation equation, and test the stability of the speed of adjustment parameter. (That is, we estimate the equation from the March quarter 1985 up until March quarter 1990, and then successively re-estimate the equation over samples that have been extended by one quarter.)[35] The speed of adjustment parameter is plotted for each sample period in Figure 13.
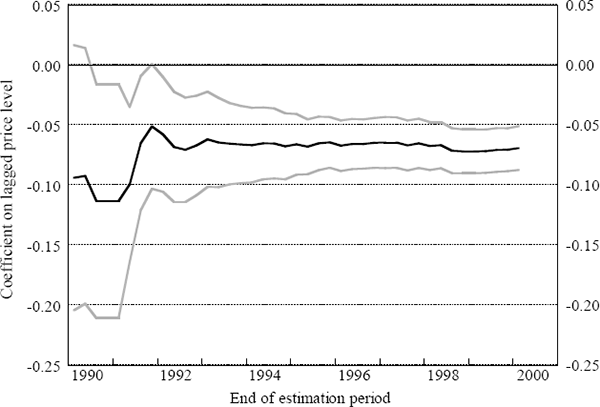
Note: The black line is the point estimate of the speed of adjustment parameter and the grey lines represent the approximate 95 per cent confidence interval of this estimate.
A widely held view is that the low inflation environment of the 1990s has been accompanied by an increase in inertia in the inflation process. If so, we would expect to see a fall in the speed of adjustment. Within the bounds of our confidence interval, such a fall is possible. However, our point estimates of the speed of adjustment parameter have been fairly stable during the 1990s.
While the speed of adjustment parameter determines the eventual length of time taken to restore long-run equilibrium following a shock, the path of adjustment to equilibrium is also influenced by short-run dynamic terms. To examine this path of adjustment, we use impulse response functions. We identify the magnitude of the response to a shock that has occurred after a given number of quarters. By using recursive estimation, we identify whether this magnitude has changed through time. The top panel of Figure 14 presents results for a permanent 1 per cent increase in import prices. Each line traces the extent to which adjustment is estimated to have occurred by the period shown. The bottom panel presents the corresponding results for unit labour costs.
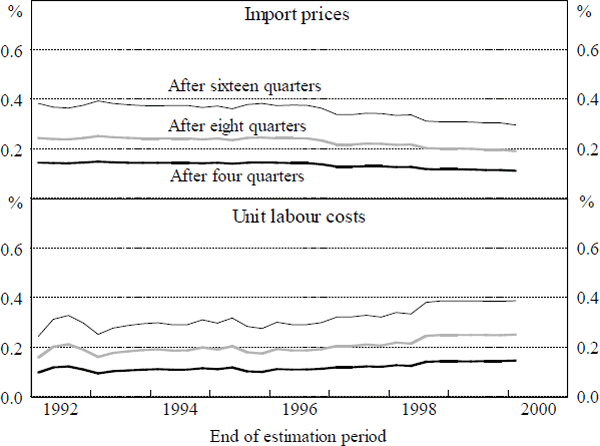
Our estimation suggests that since the mid 1990s, there has been a slight downward drift in the degree of response of consumer prices to a shock to import prices. This is most evident over time horizons greater than four quarters. The corollary of this change has been a slight upward drift in the degree of response of consumer prices to a shock to unit labour costs.[36] In each case, the degree of change is not statistically significant. The confidence intervals around the point estimates in the early part of the sample overlap with those at the end of the sample, making it unlikely that any statistical test will reject the hypothesis of ‘no change’ in the adjustment process.[37] The changes in point estimates that we observe would, however, be economically significant in the presence of large shocks to either import prices or unit labour costs.
Suppose that these point estimates of the degree of response to shocks capture actual changes in the nature of adjustment. Since the incentive to reset prices increases with the persistence of the shock to costs, one interpretation of the results is that, over the past decade, there has been a growing tendency for price setters to perceive import price shocks as transitory and unit labour costs shocks as persistent.[38] Such a change in responsiveness to shocks is consistent with low inflation outcomes because shocks to unit labour costs – that is, the more persistent of the shocks – have been relatively small, especially during the second half of the 1990s.
Two of our tests of structural stability (the Chow-type test and the examination of the speed of adjustment parameter) fail to provide evidence of a change in the inflation process during the 1990s. Our third test, which focuses on the dynamics of adjustment to a shock, gives a much stronger suggestion that a change has occurred, although the results are still not statistically significant. Ideally, to obtain a clearer picture, we would compare the degree of response to shocks in the 1990s with that in an earlier decade. In principle, this could be achieved by choosing an earlier start date for estimating our mark-up model of inflation and performing recursive regressions that, say, captured the experience of the 1980s. However, estimation of a mark-up model over longer samples is difficult, due to the major shifts in labour's share of income during the 1970s and 1980s.[39] Equations estimated over some longer samples display structural instability. Perhaps part of this instability reflects a change in the inflation process that we have not uncovered. But the popular view is that such change, should it have occurred, would be evident during the 1990s. Our results hint at some evolution of the inflation process over this period.
Footnotes
See Beechey et al (2000) for a detailed discussion of the properties of this equation. [34]
See Appendix D. The start date for estimation of the inflation equation remains the March quarter 1985 but our sample end point is more recent than that in Beechey et al (2000). Earlier start dates are often associated with structural instability that stems from the major shifts in labour's share of income in the mid 1970s and early 1980s. [35]
Linear homogeneity is accepted and imposed in the model. Therefore, a change in the estimated long-run response of consumer prices to a (permanent) import price shock is offset by an equal but opposite change in the response to a unit labour cost shock. [36]
To avoid clutter, the confidence intervals around each set of point estimates have not been drawn in Figure 14. [37]
See Taylor (2000) for a detailed analysis of the impact of perceived persistence of shocks in pricing behaviour. [38]
Given that labour's share of income is, in effect, the reciprocal of a mark-up. For a detailed discussion of the difficulty in estimating mark-up models in the presence of shifts in labour's share of income see Cockerell and Russell (1995). [39]