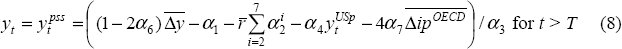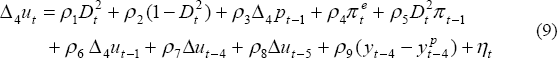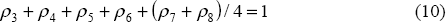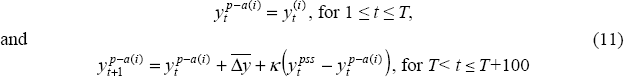RDP 2000-05: A Small Model of the Australian Macroeconomy 4. The Steady State and Potential Output
June 2000
- Download the Paper 535KB
4.1 The Steady State
We begin with assumptions about the steady-state behaviour of the exogenous variables, which are summarised in Table 6.
| Variable | Steady state property |
|---|---|
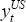
|
At the end of the estimation period, T, we derive an estimate of US potential
output, 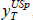 , which is then assumed to grow at
gUS = 0.875 per cent per quarter (3.5 per cent per annum), i.e., , which is then assumed to grow at
gUS = 0.875 per cent per quarter (3.5 per cent per annum), i.e.,
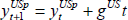 ,
t > T. While actual US output, ,
t > T. While actual US output, 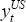 , may
differ from potential for some time into the future, they are assumed to be equal in
steady state.(a) , may
differ from potential for some time into the future, they are assumed to be equal in
steady state.(a) |
| st | st = 0. The real share price accumulation index is assumed to be at trend in steady state, so that the de-trended series, st , is zero. |
| rt | 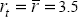 per cent per annum. The real cash rate is at neutral in steady state.
per cent per annum. The real cash rate is at neutral in steady state.Neutral is assumed to equal the average real cash rate since the early 1990s disinflation, 1993:Q1–1999:Q3. |
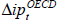
|
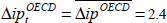 per cent per annum. OECD industrial production is assumed to grow at its average
rate over the period 1985:Q1–1999:Q3.
per cent per annum. OECD industrial production is assumed to grow at its average
rate over the period 1985:Q1–1999:Q3.
|
| tott | 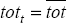 where
where 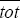 is the average of the terms of trade over the
period 1985:Q1–1999:Q3. is the average of the terms of trade over the
period 1985:Q1–1999:Q3.
|
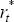
|
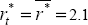 per cent per annum. The world (G3) real short-term interest rate is assumed to equal
its average over the period 1985:Q1–1999:Q3.
per cent per annum. The world (G3) real short-term interest rate is assumed to equal
its average over the period 1985:Q1–1999:Q3.
|
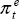
|
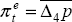 where
where 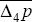 is the steady state annual rate of consumer price
inflation, which can take any constant value in the steady state (see text). is the steady state annual rate of consumer price
inflation, which can take any constant value in the steady state (see text).
|
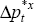
|
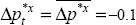 per cent per annum. Foreign (G7) export price inflation is equal to its average over
the period 1993:Q1–1999:Q3.
per cent per annum. Foreign (G7) export price inflation is equal to its average over
the period 1993:Q1–1999:Q3.
|
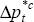
|
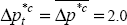 per cent per annum. Foreign (G7) consumer price inflation is equal to its average
over the period 1993:Q1–1999:Q3.
per cent per annum. Foreign (G7) consumer price inflation is equal to its average
over the period 1993:Q1–1999:Q3.
|
| Δoilt | 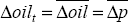 .
The Australian dollar price of oil is assumed to rise at the same rate as domestic
consumer prices. .
The Australian dollar price of oil is assumed to rise at the same rate as domestic
consumer prices.
|
Note: (a) The estimate of 3.5 per cent per annum for US potential output growth is from Rudebusch (2000). We assume that at the end of the estimation period, 1999:Q3, actual US output is 1.4 per cent above potential. This estimate is based on assuming that US unemployment was 0.7 per cent below the NAIRU at that time, and that the coefficient in Okun's Law linking changes in unemployment to output growth is 2 (this latter number is also from Rudebusch (2000)). |
|
With these assumptions for the exogenous variables, we can turn to the steady-state properties of the model's five endogenous variables. Before doing so, however, one issue needs to be resolved. The real exchange rate equation provides a description of the Australian dollar against (a weighted average of) the currencies of major trading partners, using consumer prices in each country to convert to the real exchange rate, θt. Because of data availability, however, the nominal exchange rate, et, used in the import price equation is the Australian dollar against (a weighted average of) the G7 currencies. These different definitions for the nominal and real exchange rates do not cause a problem for estimation since both variables are available over the estimation period. For simulation and forecasting purposes, and to define the properties of the steady state, however, it is necessary to relate the two variables. In the forecast period and the steady state, we assume that the two (log) measures of the real exchange rate move together, i.e.,
The behaviour of the nominal exchange rate, et, can then be derived from the
assumed behaviour of G7 consumer prices, 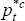 , and from the behaviour of
the real exchange rate, θt, and Australian consumer prices, pt,
derived from the model. In the steady state, the real exchange rate,
θt, is constant (see below), and consequently the nominal exchange
rate, et, appreciates (depreciates) steadily to offset any difference
between domestic and G7 consumer price inflation.
, and from the behaviour of
the real exchange rate, θt, and Australian consumer prices, pt,
derived from the model. In the steady state, the real exchange rate,
θt, is constant (see below), and consequently the nominal exchange
rate, et, appreciates (depreciates) steadily to offset any difference
between domestic and G7 consumer price inflation.
Potential output in the model is defined (see Section 4.2.1) so that actual output is equal to potential in the steady state, and therefore the output gap, the difference between actual and potential output, is zero. Table 7 summarises the steady-state properties of the model's endogenous variables.
| Variable | Steady state property |
|---|---|
| Δyt | 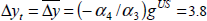 per cent per annum. Steady-state Australian
per cent per annum. Steady-state Australiannon-farm GDP growth is determined by the long-run relationship with US output in the output equation.(a) |
| Δθt | 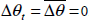 The real exchange rate is constant in the steady state because the terms of trade
and real interest rate differential are assumed constant.
The real exchange rate is constant in the steady state because the terms of trade
and real interest rate differential are assumed constant.
|
| Δpt | 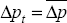 .
Consumer price inflation is constant in the steady state. .
Consumer price inflation is constant in the steady state.
|
| Δut | 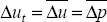 .
Unit labour cost growth is equal to consumer price inflation in the steady state. .
Unit labour cost growth is equal to consumer price inflation in the steady state.
|
| Δpmt | 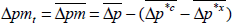 .
Import price inflation is less than consumer price inflation in the steady state
because of the Balassa-Samuelson effect (see Appendix
C). Adjusted import price inflation, however, is equal to consumer
price .
Import price inflation is less than consumer price inflation in the steady state
because of the Balassa-Samuelson effect (see Appendix
C). Adjusted import price inflation, however, is equal to consumer
priceinflation, i.e., 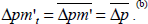 |
Notes: (a) The steady state rate of non-farm GDP growth can be
derived by setting all exogenous variables in the output equation to their
steady-state values, and taking first differences of the equation. |
|
Recall the series of homogeneity restrictions that are imposed on the estimated equations. The unit labour cost equation exhibits dynamic homogeneity (a vertical long-run Phillips curve) in the latter part of the sample, and in the steady state. Both the consumer price and import price equations exhibit static homogeneity but neither equation exhibits dynamic homogeneity.
These restrictions have several implications for the model. The model is neutral in the long run with respect to changes in the price level; that is, no real variables are affected in the long run as a consequence of a change in the price level. With respect to changes in the steady-state rate of inflation, Δp, however, most real variables are unaffected, but not all. Output and the real exchange rate are unaffected. But the lack of dynamic homogeneity in the consumer price equation implies that changes in the steady-state rate of inflation have a permanent effect on the level of real unit labour costs, u − p. This result is at odds with our theoretical expectations, although there is empirical evidence that it may be a widespread phenomenon (Banerjee and Russell 1999).
Furthermore, the lack of dynamic homogeneity in the import price equation implies that changes in the steady-state rate of import price growth (matched by changes in the rate of nominal depreciation and/or foreign export price growth) have a permanent effect on the margin between the cost of imported goods and their landed prices. While it is plausible that this margin would move in the short run (due to a variety of factors including incomplete exchange rate pass-through, lags in contract renegotiation etc), it is hard to understand why it would shift permanently in response to a change in the steady-state rate of import price growth.
Finally, note that consumer price inflation in the steady state can take on any constant value,
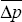 . When the
model is augmented with a policy reaction function, however, consumer price inflation in the
steady state is determined by the monetary policy authorities.
. When the
model is augmented with a policy reaction function, however, consumer price inflation in the
steady state is determined by the monetary policy authorities.
4.2 Potential Output
Potential output plays two roles in the model. Firstly, it is the level of output consistent with steady inflation (assuming both inflation expectations and unit labour cost growth are equal to price inflation). It plays this role over both the estimation period and in any simulation of the model into the future (which will usually involve adjustment to the model's steady state). Secondly, potential output must be consistent with actual output in the steady state of the model.[10]
This section explains how potential output is calculated so that it plays both these roles. We begin by defining two potential output series, one in the steady state, and the other in the estimation period, which we then splice together to generate a smooth series with the required properties.
4.2.1 Potential output in the steady state
We derive the level of actual, and therefore potential, output in the steady state from the
output equation, Equation (1). Setting all exogenous variables to their steady state values,
non-farm growth at its steady state rate, 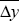 (given in Table 7), and
the error term to zero, gives
(given in Table 7), and
the error term to zero, gives
where 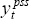 denotes
potential output in steady state, and US potential output,
denotes
potential output in steady state, and US potential output, 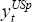 , is
assumed to be
, is
assumed to be 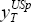 at the end of the estimation period, T, and
at the end of the estimation period, T, and 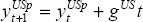 , for
t > T, as in Table 6.
, for
t > T, as in Table 6.
4.2.2 Potential output in the estimation period
Potential output in the estimation period is defined so that the unit labour cost equation has a vertical long-run Phillips curve in the latter part of the sample. That equation (repeated here for convenience) is
where 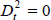 for
t ≤ 1995:Q4,
for
t ≤ 1995:Q4, 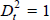 for t ≥ 1996:Q1. The
restriction
for t ≥ 1996:Q1. The
restriction
is accepted by the data and imposed when the equation is estimated (see Table 4).
When t ≥ 1996:Q1 and output is at potential, the equation is consistent with steady inflation (with inflation expectations equal to both unit labour cost and consumer price inflation) only when ρ1 = 0. We use this observation to adjust the level of potential output so that this restriction on ρ1 is satisfied.
4.2.3 Deriving potential output
We proceed as follows. We begin by defining potential output as a Hodrick-Prescott filter of
actual output, 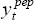 , over a period, 1 ≤ t ≤ T,
starting before the estimation period and running to its end. [11] We then estimate the
unit labour cost equation, Equation (9), over the estimation period, with the restriction
Equation (10) imposed. This generates a non-zero estimate for ρ1 in
general. We then generate an adjusted output series by
, over a period, 1 ≤ t ≤ T,
starting before the estimation period and running to its end. [11] We then estimate the
unit labour cost equation, Equation (9), over the estimation period, with the restriction
Equation (10) imposed. This generates a non-zero estimate for ρ1 in
general. We then generate an adjusted output series by 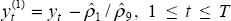 . This
adjustment is designed so that, had the unit labour cost equation been estimated using the H-P
filter of
. This
adjustment is designed so that, had the unit labour cost equation been estimated using the H-P
filter of 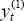 as
the potential output series rather than
as
the potential output series rather than 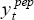 , the resulting estimate,
, the resulting estimate,
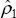 , would have
been zero.
, would have
been zero.
We now splice the two series, 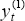 for 1 ≤ t ≤ T,
and
for 1 ≤ t ≤ T,
and 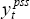 for
t > T (from Equation (8)), to generate a single smooth series for potential
output. We do this by generating a partial-adjustment series,
for
t > T (from Equation (8)), to generate a single smooth series for potential
output. We do this by generating a partial-adjustment series, 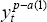 ,
defined (for i = 1) by
,
defined (for i = 1) by
where κ is a speed-of-adjustment parameter, set equal to 0.05. The smooth
potential output series, 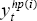 , is then generated as the H-P filter (with
smoothness parameter 5,000) of the partial-adjustment series,
, is then generated as the H-P filter (with
smoothness parameter 5,000) of the partial-adjustment series, 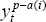 , 1 ≤
t ≤ T+100.
, 1 ≤
t ≤ T+100.
In general, the smooth potential series, 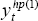 , and the H-P filter of
, and the H-P filter of
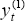 , are very
similar over the estimation period, but not identical. As a consequence, when the unit labour
cost equation (with the restriction Equation (10) imposed) is
re-estimated using
, are very
similar over the estimation period, but not identical. As a consequence, when the unit labour
cost equation (with the restriction Equation (10) imposed) is
re-estimated using 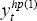 as the potential series, the resulting estimate,
as the potential series, the resulting estimate,
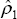 , will be
non-zero. We therefore iterate, defining a new adjusted output series,
, will be
non-zero. We therefore iterate, defining a new adjusted output series, 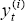 (for
i = 2) by
(for
i = 2) by 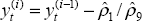 , 1 ≤ t ≤
T, where
, 1 ≤ t ≤
T, where 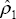 and
and 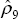 are the
estimated parameters using
are the
estimated parameters using 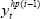 as potential output. We then calculate a
new partial-adjustment series using Equation (11) and a new smooth potential series,
as potential output. We then calculate a
new partial-adjustment series using Equation (11) and a new smooth potential series, 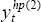 .
.
This process is repeated until, after a few iterations, the resulting smooth potential series,
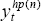 , generates an
estimate,
, generates an
estimate, 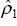 , in
the unit labour cost equation that is (arbitrarily close to) zero. This is then the potential
output series,
, in
the unit labour cost equation that is (arbitrarily close to) zero. This is then the potential
output series, 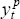 , used in the estimated equations reported in Section 3 of the paper.
, used in the estimated equations reported in Section 3 of the paper.
Figure 6 shows the annual growth rate of potential output, 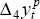 , over
the estimation period and into the future. At the end of the estimation period, potential output
is estimated to be growing at around 3.8 per cent per annum, very similar to its rate of growth
in the steady state.
, over
the estimation period and into the future. At the end of the estimation period, potential output
is estimated to be growing at around 3.8 per cent per annum, very similar to its rate of growth
in the steady state.
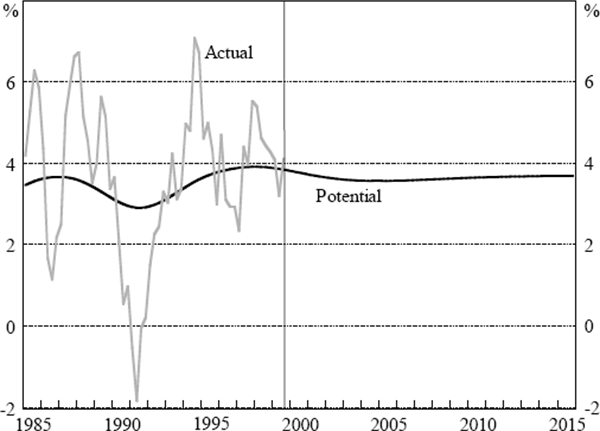
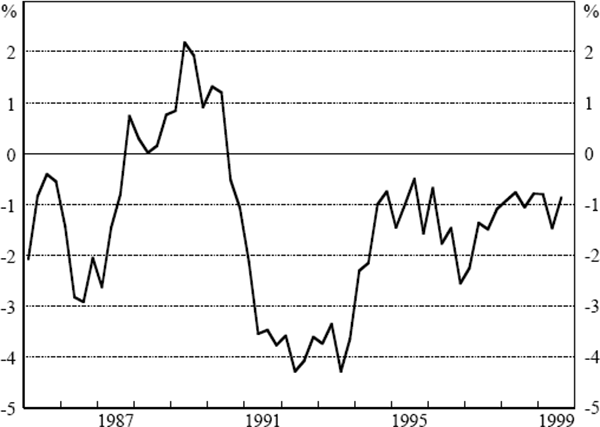
Figure 7 shows the estimated output gap over the estimation period. An output gap of zero is consistent with steady inflation when inflation expectations and unit labour cost growth are both running at the same rate as consumer price inflation. If inflation expectations are above actual inflation, however, output must be kept below potential (as defined here) in order to keep inflation steady.[12]
Footnotes
Strictly speaking, we model potential non-farm output but we use the simpler term ‘potential output’ for ease of exposition. [10]
Starting the H-P filter in t = 1 = 1974:Q3, well before the beginning of the estimation period, avoids starting-point problems with the filter. As will become clear, we also extend the analysis for 100 quarters beyond the end of the estimation period to avoid end-point problems. We use a smoothing parameter of 5,000 in the filter, because smaller values generate considerable variation in potential output growth at business-cycle frequencies. [11]
Over the estimation period, inflation expectations derived from the bond market have exceeded actual inflation by an average of 1.2 percentage points per annum. If this average difference were to persist, it would be necessary for output to remain an average 0.7 per cent below potential in order to keep inflation steady. (This result can be derived from the coefficients on bond market inflation expectations and the lagged output gap in the unit labour cost equation.) [12]