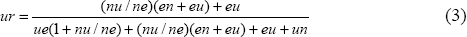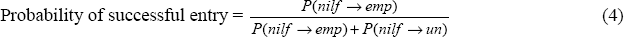RDP 1999-12: Unemployment and Skills in Australia 4. Why is Unskilled Unemployment Higher?
December 1999
- Download the Paper 389KB
The evidence presented in the previous two sections demonstrates that unemployment rates are generally much higher for unskilled workers than for skilled workers, both in Australia and overseas. Why this should be the case is not immediately obvious. A simple competitive model predicts that lower unskilled productivity should be reflected in correspondingly lower wages (and perhaps lower labour-force participation rates), and not in higher unemployment. Moreover, a number of non-market-clearing models of the labour market contain features that actually predict that skilled unemployment should be higher than unskilled unemployment. For example, skilled work may be more difficult to monitor effectively than unskilled work, which in a worker-discipline model (e.g. Shapiro and Stiglitz 1984) would imply a greater incentive to shirk among skilled workers, leading to higher unemployment for this group. Alternatively, we might expect the wage distribution of job offers to be wider for a skilled worker than for an unskilled worker. In a search framework such as Pissarides (1990), this would lead skilled workers to reject job offers which do not provide a good fit to their skills set, increasing skilled unemployment.[14]
4.1 Transition Probabilities
One plausible reason why unskilled unemployment is relatively high is that unskilled workers have less firm-specific human capital than skilled workers. Since firm-specific human capital is dissipated when skilled workers leave employment, they, and their employers, have an incentive to reduce such separation. As a result, the separation rate (the rate at which currently employed workers leave employment) is higher for unskilled workers. This in turn leads to a higher equilibrium unemployment rate for this group.
A useful exercise to help appraise this and other explanations for the large steady-state differences between unemployment rates is to examine gross flows between labour market states for different skill groups. We calculate these flows using data on individuals from the Survey of Employment and Unemployment Patterns (SEUP).[15] The SEUP survey, as well as containing a large sample of job-seekers, also includes a Population Reference Group of 2,311 individuals, designed to reflect the labour market characteristics of the population as a whole. From these data, we calculate the average probability of moving between three labour market states (employment, unemployment and out of the labour force). We calculate this for four different levels of educational attainment: bachelors degree or above, non-degree tertiary education, completed high school and did not complete high school. Average transition probabilities over Wave 1 and Wave 2 are presented in Table 3.
| Degree level education or higher | |||
|---|---|---|---|
| Em | Un | Nilf | |
| Em | 99.0% | 0.4% | 0.6% |
| Un | 16.8% | 77.2% | 6.0% |
| Nilf | 7.1% | 3.3% | 89.7% |
| Completed high school | |||
| Em | 97.9% | 0.9% | 1.2% |
| Un | 10.5% | 86.9% | 2.6% |
| Nilf | 4.2% | 2.4% | 93.4% |
| Other tertiary education | |||
| Em | 98.8% | 0.5% | 0.7% |
| Un | 10.9% | 86.6% | 2.5% |
| Nilf | 3.4% | 2.0% | 94.6% |
| Did not complete high school | |||
| Em | 98.0% | 1.0% | 0.9% |
| Un | 8.9% | 89.0% | 2.0% |
| Nilf | 1.9% | 1.4% | 96.7% |
| Notes: Old labour force status is listed down the column, new labour force status is listed across the row, monthly probabilities. Transition probabilities are measured as the average proportion of individuals in one labour market state that shifted to a particular other state over the period between two reference points a month apart. | |||
Consistent with the gross flows data in the Labour Force Survey, data in Table 3 are presented in the form of monthly transition probabilities, ie. by comparing the labour force status of a worker from one month to the next. The overall magnitude of these flows is consistent with the Labour Force Survey.
There are several differences between the transition probabilities for skilled and less-skilled labour. Firstly, transitions from employment to unemployment occur much more frequently for less-educated workers. An individual who did not complete high school is 2½ times more likely to enter unemployment from employment over the course of a month than is an employed degree educated individual. Furthermore, the probability of an unemployed university graduate finding employment over the course of a month is 16.8 per cent, compared with 10.0 per cent for those with other tertiary qualifications, and 8.9 per cent for unemployed individuals who had not completed high school. Since more-educated individuals also have a higher transition rate from unemployment to outside the labour force, the duration of unemployment is therefore substantially longer for a less-educated individual.[16]
We are now in a position to examine to what extent differences in transition probabilities between education groups account for differences in unemployment rates between these groups. In equilibrium, the number of employed, unemployed and non-participating individuals remains constant (given a constant sample size). Following the approach of Foster and Gregory (1982), we can use this property to calculate the steady-state unemployment rate for each group as a function of transition probabilities, as shown below. (Appendix B explains in more detail how this expression is derived.)
We then calculate the marginal impact of the individual transition probabilities on the overall unemployment rate for each education group. To do this, we replace the relevant transition probability for one group of workers (say ‘completed high school’) with the relevant transition probability from the ‘bachelors degree or higher’ group. We then calculate a new steady-state unemployment rate for the group, and compare it with the original steady-state unemployment rate. This approach allows us to examine the marginal impact of each transition probability or sets of transition probabilities on the different steady-state unemployment rates.
A summary of these results is presented in Table 4. In steady state, the ‘completed high school’ unemployment rate is 7.1 percentage points above the unemployment rate for degree educated individuals, while the ‘did not complete high school’ rate is 9.6 percentage points higher than the degree rate. However, if the job separation rate (the sum of transition rates from employment to unemployment and employment to outside the labour force) was the same for these groups as for the degree educated group, these steady state unemployment differences would fall to 3.2 percentage points and 2.1 percentage points respectively.[17] Mostly, this difference reflects differences in the transition rates from employment to unemployment between education groups.
| Other tertiary | Completed high school | Not completed high school | |
|---|---|---|---|
| Steady-state difference from degree unemployment rate | 2.8% | 7.1% | 9.6% |
| Marginal effect of transition probabilities: | |||
| Employment to unemployment (eu) | 0.5% | 3.2% | 5.1% |
| Employment to outside the labour force (en) | 0.4% | 1.7% | 1.1% |
| Job separation rate (eu and en) | 0.9% | 5.0% | 6.4% |
| Unemployment to employment (ue) | 1.7% | 3.1% | 5.0% |
| Not in labour force to employment (ne) | 0.9% | 1.2% | 2.2% |
| Job matching rate (ue and ne) | 2.3% | 3.9% | 6.2% |
| Transitions between unemployment and not in the labour force (un and nu) | −0.04% | 0.6% | −0.4% |
Notes: Values in this table represent the marginal impact of each transition probability or set of transition probabilities on the group steady-state unemployment rate. These are calculated by replacing the transition probability for the education group with the corresponding probability for degree-educated individuals. A full set of results and a more complete explanation of the method used are presented in Appendix B. |
|||
Alternatively, if the matching rate (the rate at which non-employed workers are matched to jobs) were the same for all education groups, the steady state unemployment differences would fall to 0.5, 3.2 and 3.4 percentage points for the non-degree-tertiary-educated, completed high school and not completed high school groups respectively. Partially, this is because less-educated individuals have a lower probability of entering the labour market successfully (i.e. that they are more likely to move from outside the labour market to unemployment, rather than into employment). We can calculate the probability of a successful entry into the labour market – that is, into a job rather than the unemployment pool – as:
where P(nilf→emp[un]) is the conditional probability of moving from outside the labour force to employment [unemployment]. Sixty-eight per cent of degree-educated workers entering the labour force during a month find employment by the end of the month. This falls to 64 per cent for those with non-degree tertiary qualifications, 63 per cent for those who have completed high school but gone no further, and 59 per cent for individuals who have not completed high school.
Differences in transition rates between unemployment and outside the labour force play a more minor role in accounting for unemployment differentials. Note that since the relationship in Equation (2) is not linear, the marginal effects of individual transition probabilities shown in Table 4 are not additive. That is, the sum of the effects of changing (for example) the ue and ne transition probabilities individually is different from the effect of changing ue and ne at the same time.
We conclude that the high unemployment of less-educated workers can be attributed to two main factors: (i) a less-educated worker has a greater probability of exiting employment each period (a high ‘separation rate’), and (ii) once not employed, a less-educated worker has a smaller probability of finding employment (a low ‘matching rate’). These two influences are of approximately equal importance. In contrast, Foster and Gregory (1982), who use the same framework, find that separation rates alone explain nearly all the difference in unemployment rates between teenagers and adults over the year ended June 1980. Our findings suggest that across education groups, both separation and matching rates are important for explaining unemployment differentials.
Although these results are revealing, they are limited in several respects, and a number of extensions exist for future research. Firstly, the SEUP survey on which our results are based consists of a relatively small sample of only 2,311 individuals. The sampling error associated with our estimates could be substantial. Secondly, transition probabilities fluctuate substantially over the course of the business cycle (Blanchard and Diamond (1990), and Debelle and Swann (1998) for recent Australian evidence). With only two years of data, we have no satisfactory way of accounting for this cyclicality. We can gain some comfort from the fact that the average output gap over the period of our data, September 1994 to September 1996, was quite close to zero (based on the estimates in de Brouwer (1998)), suggesting that the observed transition probabilities were close to the equilibrium probabilities. A third caveat is that each of the transition probabilities are related. It would certainly not be possible in practice to change one transition probability without affecting each of the other probabilities at the same time. A more comprehensive study might try and explain the transition probabilities in terms of deeper structural variables, rather than treating them as exogenous (in the spirit of Mortensen and Pissarides (1994)).
4.2 Explanations
We are now in a position to discuss and evaluate possible explanations for the high rate of unskilled unemployment. We consider four commonly cited explanations below. The first explanation is more relevant for explaining differences in separation rates across skill groups, the other three explanations may help to explain why the matching rates of unskilled workers are lower than for skilled workers. We present relevant empirical evidence where possible, but given available data it is difficult to determine with any degree of certainty which explanation is most important.
4.2.1 Firm-specific human capital
Unskilled workers are generally thought to have less human capital, and in particular less firm-specific human capital, than skilled workers (Nickell and Bell 1995). An individual with firm-specific skills has a high value to the firm relative to their market value; in a search framework, separations between workers and jobs will occur less frequently for these workers. Thus, we might expect the separation rate of workers from jobs to be higher for less-skilled labour market groups. Certainly, this expectation is consistent with our data on transition probabilities. Less-skilled workers have much higher exit probabilities from employment, both into unemployment and to outside the labour force.
We might also expect a high degree of firm-specific capital to increase the amplitude of fluctuations in unskilled unemployment rates relative to skilled rates. During recessions firms will hoard the human capital embodied in their skilled labour force, and instead shed unskilled labour. The evidence for ‘excess amplitude’ in unskilled unemployment is, however, weak. We de-trend the unemployment rates for different education groups (from the information presented in Figure 6), and calculate the standard deviation for each group in turn. We compare this to the degree of variability predicted by the Nickell and Bell model. Since the Nickell and Bell framework does not take hoarding of skilled labour into account, the actual standard deviation should rise relative to the predicted standard deviation for less-educated groups.
A summary of these results is presented in Table 5.
| Males | Females | ||||
|---|---|---|---|---|---|
| Actual | Predicted | Actual | Predicted | ||
| University Degree | 0.77 | 0.77 | 1.26 | 1.26 | |
| Trade/Diploma | 1.66 | 1.14 | 1.25 | 1.68 | |
| Completed high school | 2.17 | 1.63 | 1.24 | 2.04 | |
| Not completed high school | 2.05 | 1.73 | 1.53 | 2.00 | |
Note: These are the de-trended standard deviations of unemployment for each skill groups, from the data presented in Figure 6. |
|||||
For males, it is certainly true that the standard deviation of unemployment rates increases as the level of skill falls, and more so than would be predicted by the Nickell and Bell framework. However, for females the opposite is true. Not only is the actual unemployment standard deviation less than predicted, but even the stylised fact that unemployment rates are more variable for the less-skilled does not hold true for females (except for the not completed high school group).
Thus, the evidence is somewhat mixed. The high separation rates for unskilled workers are consistent with an explanation based on firm-specific human capital. However, other explanations for high unskilled unemployment must be at least equally important, since differences in separation rates explain only part of the unemployment differences between skill groups. The following three explanations may all help to explain why the matching rate of workers to jobs is higher for skilled labour than for unskilled labour.
4.2.2 Skilled labour performing unskilled jobs
Skilled workers are able to search for both skilled and unskilled jobs, whereas unskilled workers do not have this luxury. Thus, a skilled worker who is unable to obtain employment in their area of specialisation can ‘trade down’ to a less-skilled position while continuing to search for a skilled job. In a search model that permits on-the-job search, this will reduce the equilibrium unemployment rate of skilled workers by increasing the matching rate of workers to jobs. However, as McCormick (1990) argues, skilled workers may be unwilling to accept unskilled employment even for short periods of time due to fears of stigmatisation.
Data from the SEUP survey give an indication of the proportion of workers who are ‘overqualified’ for the position they hold. Table 6 compares the highest level of education obtained by employed workers to the level of education actually required to do their job. As expected, a substantial majority of degree-educated workers have employment requiring a degree qualification. However, some 18 per cent of these workers hold employment which require no qualifications whatsoever. Moreover, 63 per cent of those with other post-school qualifications such as a trade qualification or undergraduate diploma have employment requiring no qualifications. Hecker (1992) finds an identical result – that 18 per cent of US college graduates are working in unskilled jobs. However, Tyler, Murname and Levy (1995) show that many of these are young workers who subsequently find employment in a skilled career path.
| Highest level of Education |
Level of qualifications required for job | ||||
|---|---|---|---|---|---|
| Degree | Post-school | High school | No quals. | Obs. | |
| Degree | 69% | 12% | 1% | 18% | 43 |
| Post-school | 2% | 33% | 1% | 63% | 99 |
| High school | 0% | 16% | 7% | 77% | 85 |
| NCHS | 0% | 6% | 6% | 88% | 135 |
| Obs. | 31 | 55 | 17 | 259 | 362 |
Notes: Sample is all employed people at the end of Wave 1 who are in the population reference group, and who answered the questions ‘What is your highest level of educational attainment?’ and ‘What level of education is required for your job?’. Only the primary job of each respondee is included. The number of observations is the raw number of respondees. The percentages have been weighted using the population reference group weights supplied in SEUP so that the sample reflects the characteristics of the labour force as a whole, rather than the sampling characteristics of the SEUP survey. |
|||||
We also used the SEUP data to examine whether educated workers in ‘uneducated’ jobs tend to then move into an ‘educated’ job. The available data suggest that this is not the case – these workers predominantly remain in unskilled jobs despite their high education level. However, in making this calculation our sample size becomes so small that we are unable to draw any firm conclusions.[18]
Okun (1981) argues that the ‘crowding out’ of unskilled jobs by skilled workers will also change the composition of unemployment across skill groups over the business cycle. In his model, wages are sticky, and so employers adjust the hiring standard instead – thus giving a higher share of unskilled jobs to skilled labour when unemployment is high. Van den Berg et al (1998) test for the existence of cyclical crowding out of unskilled workers using firm-level data from the Netherlands. They find no evidence that skilled workers replace unskilled workers disproportionately during recessions. However, they do find that the average education level of workers in all job types increased in the Netherlands over the first half of the 1990s, perhaps suggesting that credential creep was occurring.
The evidence that a substantial number of workers (especially in the non-degree tertiary education group) are overqualified for the jobs they hold may reflect crowding out of less-skilled jobs by overqualified workers. Unfortunately, we are unable to examine how crowding out varies over the cycle. Ideally, we would like data on how matching rates by education group vary as the unemployment rate fluctuates; using such data, we could test whether the degree of ‘credential creep’ increases when the unemployment rate is high, as the Okun (1981) hypothesis would imply.
4.2.3 Replacement ratios
The replacement ratio (the ratio of a person's unemployment benefit to the wage they would earn if employed) is often used to measure the relative incentive of an unemployed person to search for work. In a search model like Pissarides (1990) the size of the replacement ratio is positively related to the equilibrium unemployment rate. Other authors have highlighted the duration of benefits as a factor which reduces search intensity (e.g. Layard, Nickell and Jackman 1991), and thus reduces the matching rate of workers to jobs.
Since the level of unemployment benefit paid in Australia is not related to previous income, and since skilled wages are substantially higher than unskilled wages, the replacement ratio will be higher for unskilled workers than for skilled workers. Dawkins, Harris and Loundes (1998) find a higher replacement ratio to significantly reduce an individual's probability of being in employment (conditional on other worker characteristics), using longitudinal data on Australian female youth. Whether this result generalises to the population as a whole is an unresolved question. The disincentive effect of a high replacement ratio would reduce the transition probability from unemployment to employment. Consistent with the hypothesis, the evidence presented in Section 4.1 shows that this transition probability is much lower for unskilled workers than for skilled workers.
4.2.4 Compressed wage distribution
In addition to the mechanisms outlined above, any tendency for the wages of less-skilled workers to be higher (relative to a competitively determined wage) than the wages of more-skilled workers, will tend to increase unskilled unemployment. Under such a scenario, low-productivity workers are relatively ‘overpaid’, and thus are relatively less attractive to employers.
For this explanation to be the most important one, any ‘compression’ of the wage distribution must affect not just very low-skilled workers, but also individuals higher up the wage distribution. Why? Because unemployment rates of semi-skilled workers are still substantially higher than unemployment rates of highly skilled workers.
Compression in the wage distribution could be due to institutional or non-institutional factors. In Australia, the award system is a potential institutional cause. Since the award structure affects workers across a wide range of skill levels, it could explain the cascading increases in average unemployment rates at progressively lower levels of skill. But it seems unlikely that such country-specific institutional factors are the main explanation, since Figure 1 shows that unskilled unemployment is comparatively high across a wide range of countries with very different institutional features.
Are there any underlying features of labour markets that could lead to a compression of the wage distribution, independent of institutional factors? Various academic theories of wage rigidity suggest possibilities along these lines. For example, Akerlof and Yellen (1990) develop an efficiency-wage explanation based on a ‘fair-wage hypothesis’. They argue that a worker's effort will fall if they are paid a wage below that which they consider to be fair, and moreover that this fair wage will be affected by the wage paid to other workers in the firm or the economy more generally.[19] This dependence will increase the ‘fair’ wage for unskilled workers and decrease the ‘fair’ wage for skilled workers. An analytical model based on the fair wage assumption predicts that unskilled unemployment will be higher than skilled unemployment, and that the relationship between the two unemployment rates will be uncorrelated with changes in aggregate unemployment. These predictions provide a reasonable characterisation of the Australian evidence on unemployment presented in Section 3.
Footnotes
This conclusion is less convincing if we consider a model that allows workers to search for new jobs while employed (Pissarides 1994). [14]
The SEUP survey was conducted in a series of ‘waves’. An interview was conducted during each wave, during which the respondent provided details of their job-search activities over the previous twelve months. In this paper we use data from Wave 1 and Wave 2, covering labour market experiences from September 1994 to September 1996. [15]
The average completed duration of unemployment in months is equal to 1/[P(un → emp) + P(un → nilf)]. [16]
Calculated as 7.1 − 5.0 = 2.1 percentage points, and 9.6 − 6.4 = 3.2 percentage points. [17]
Our approach is to observe the proportion of workers with post-school education who are working in jobs requiring no qualifications whose next job requires post-school qualifications. Unfortunately, due to the high non-response rate to the questions required for this calculation, we are left with only 18 observations. Of these 18 workers, 16 remained in a non-qualification job, and only 2 shifted to a job requiring post-school qualifications. [18]
One piece of evidence quoted by the authors consistent with this argument is that differences in wages between different firms and industries are highly correlated across workers of different skill levels. [19]