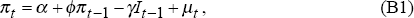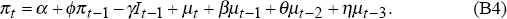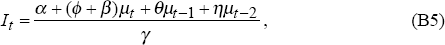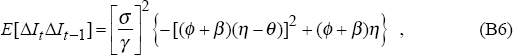RDP 9703: The Implementation of Monetary Policy in Australia Appendix B: A Model of Interest-rate Adjustment

Goodhart and Huang (1996) present a simple model in which the policy interest rate varies randomly around a constant mean. Their starting point is the following inflation process,

where: π is the inflation rate, I is the policy interest rate and μ is a serially uncorrelated shock to inflation.^[22] One could think of this shock as an ‘exogenous’ change in the exchange rate or wages. In this model, inflation is persistent and interest rates affect inflation with a lag. The central bank is assumed to know with certainty that this model represents the true inflation process, and it also knows the parameters with certainty. The objective of the bank is to minimise the expected discounted squared deviations of inflation from some desired level (π^*): that is, it minimises,

subject to Equation (B1). Without loss of generality we assume that π^* is equal to zero. Solving the model, the optimal interest rate at any point in time is given by

This rule means that the central bank sets the interest rate at the point where in expectation it achieves its inflation objective. Given that μ is a random variable, the level of the interest rate is also a random variable (around a constant mean), with past movements providing no information regarding the future level of interest rates. This leads Goodhart and Huang to conclude that in a model with persistence and lags, and with the central bank caring only about inflation, there should be no interest-rate smoothing.

Now consider what happens when we change the inflation process to the following,

The change here is that the shocks to inflation have different dynamic effects on inflation than do changes in the interest rate. For particular values of the parameters, this model allows the inflationary impact of the shock to build over time and then to dissipate.

In this model the optimal interest rate rule is given by

and the autocorrelation of interest rate changes by

where σ is the standard deviation of the inflation shock.

Under some sets of parameters, the optimal interest-rate response to an inflation shock is to increase the interest rate twice and then to reduce the interest rate in two steps back to its initial value – similar to the general pattern observed in practice. Whether or not such a pattern generates positively correlated changes in interest rates on average, again depends upon the particular parameters. If η and θ are close in magnitude, then interest-rate movements are likely to exhibit positive autocorrelation. In contrast, if η is zero, the correlation between interest-rate changes will be negative.

Footnote

All parameters are assumed to be non negative and the policy interest rate is chosen after the shock is known. [22]