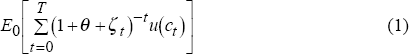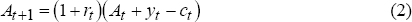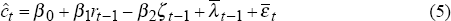RDP 9602: Consumption and Liquidity Constraints in Australia and East Asia: Does Financial Integration Matter? 2. The Euler Equation with Liquidity Constraints
May 1996
- Download the Paper 346KB
This section provides a simple motivation for the equation used to examine the behaviour of consumption. The literature on consumption smoothing is extensive and well summarised by Hall (1989), Deaton (1992), Muellbauer (1994) and Muellbauer and Lattimore (1994). The model used here is based on Hall (1978) but includes demographic change, which is a major structural feature of East Asian economies World Bank (1993, pp. 38–40), and, following Muellbauer (1983) and Zeldes (1989), a liquidity constraint, which is the factor commonly cited for the failure of the basic Hall model.
The representative household is assumed to maximise a concave expected utility function:
where E0 is the subjective expectation at time 0 based on all available information, ct is consumption, θ is the pure time discount, and ζt is the time discount varying in the demographic change particular to the country, assumed to be increasing in expected mortality and the birth of new cohorts (Masson 1992 and Schmidt-Hebbel, Webb and Corsetti 1992). The household faces three constraints, the first being that its assets accumulate according to the rule:
where At+1 is end-period t net wealth, including financial wealth and real wealth such as housing and durables, yt is labour income, rt is the real interest rate and ct is consumption. Secondly, given no bequest motive, the no-Ponzi game outcome requires that net assets are zero at the terminal date, T:
This means that the present value of lifetime expected consumption is tied to the present value of lifetime expected income – consumption is always ‘constrained’ in the sense that income is limited and the bliss-point for consumption never reached. This is not, however, the meaning of ‘liquidity constrained’. A liquidity constraint may exist for a number of reasons and hence may take on a number of forms. One form, outlined by Muellbauer (1983) and Zeldes (1989), is that household net assets plus saving be non-negative each period:
Assuming that utility is isoelastic, in the form 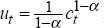 , constrained
optimisation yields the familiar first-order condition:
, constrained
optimisation yields the familiar first-order condition:
where 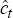 = Δlnct (consumption growth rate) and
= Δlnct (consumption growth rate) and 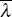 is
a variant of λ. As summarised by Hall (1989), when the constraint of
non-negative net worth is binding, the household is denied access to its stream of future
income. It is forced to reduce current consumption in favour of future consumption to equate
marginal utilities over time, much as it would if it faced a higher interest rate. The
constraint does not mean that the household consumes all its current income. Rather, the
liquidity constrained household smooths consumption but, given a concave utility function, the
more binding the constraint, the lower is current consumption, and the higher is future
consumption. Hall's (1978) famous prediction that consumption follows a random walk does not
follow in the presence of liquidity constraints.
is
a variant of λ. As summarised by Hall (1989), when the constraint of
non-negative net worth is binding, the household is denied access to its stream of future
income. It is forced to reduce current consumption in favour of future consumption to equate
marginal utilities over time, much as it would if it faced a higher interest rate. The
constraint does not mean that the household consumes all its current income. Rather, the
liquidity constrained household smooths consumption but, given a concave utility function, the
more binding the constraint, the lower is current consumption, and the higher is future
consumption. Hall's (1978) famous prediction that consumption follows a random walk does not
follow in the presence of liquidity constraints.
There are four issues to deal with before equation (5) can be used as an estimating equation. The first is aggregation over time. Annual data are used in the estimation because the demographic data and, for most countries, the expenditure and income data are only available on an annual basis. Moreover, expenditure data, particularly on a quarterly basis, are constructed using extrapolated data based on periodic and occasional surveys, and this introduces a degree of smoothing and measurement error in the series which can be minimised by using annual data. However, this renders equation (5) unsuitable as the basis for an estimating equation. When the consumption decision is made continuously or within a short period, such as a week, fortnight or month, then variables which are lagged once in equation (5) are approximately current-dated on an annual basis. For example, if the household's non-durables expenditure plan is tied to the profile of its income payments, which is, say, monthly, then the consumption decision is monthly and the real interest rate, demographic change and liquidity constraint in the previous month are relevant to the consumption decision in the current month. But on annual data, the interest rate etc in the previous month are contemporaneous in eleven cases out of twelve and well approximated by the current-dated variable. Equation (5) then reduces to a regression on current-dated variables.[1]
The second issue is aggregation across households. There has been considerable demographic change in East Asian economies over the past few decades, as strong population growth has eased and longevity and the share of the aged in the population has increased. Change also varies considerably between countries. Lahiri (1989), Takahashi and Kitamura (1993), Shintani (1994) and Lattimore (1994), to name a few, have shown the empirical importance of this for saving or consumption decisions in various economies in the region. Three differenced variables, defined in Table 1 and plotted in levels in Appendix A, are included in the estimating equation in the form of a time-varying discount factor in the utility function in equation (1). First differences are used to capture change.
| Variable | Definition |
|---|---|
| d0–19 | first difference of ratio of population aged 0–19 years to total |
| d65 | first difference of ratio of population aged >64 years to total |
| ddepend | first difference of ratio of population aged 0–19 and >64 years to total |
The third issue is how to model the shadow price of the constraint. Since it is not observable, various proxies, termed z, are used. Liquidity constraints (and hence a positive shadow price) may exist for a number of reasons. Firstly, domestic financial markets may be repressed or insufficiently developed, or capital controls which impede access to international financial markets may exist. Secondly, when information about the borrower's credit risk is incomplete or asymmetric, the possibilities of moral hazard and adverse selection indicate that would-be borrowers may be denied access to capital markets (Stiglitz and Weiss 1981), at least until they have proven their reliability which may be related to age and experience (Scheinkman and Weiss 1986). Thirdly, lenders may prefer to extend credit secured by financial or real assets rather than on the basis of expected future labour income since lenders cannot indenture labour but can seize assets (Faruqee, Laxton and Symansky 1995). Would-be borrowers without capital may find it more difficult to obtain funds than would-be borrowers with capital (Cox and Jappelli (1993) provide evidence for the US). If wealth is acquired over time or is increasing in human capital, then younger or unskilled people are more constrained than older or skilled people.
These reasons suggest a range of variables which may be used as a proxy for the shadow price. If financial repression is the source of the constraint, for example, financial variables, such as real credit growth, the spread between money market and deposit rates or between loan and deposit rates and financial depth may be correlated with the liquidity constraint. Consider these in turn. Real credit growth is a constraint when there are controls on bank lending through window guidance. It is expected to be positively correlated with consumption since an expansion of credit reduces the constraint. Interest rate spreads are a function of, among other things, interest rate regulation and the depth and development of the banking sector (de Brouwer 1995), and are expected to be negatively correlated with consumption. Financial depth, commonly proxied by the ratio of money to GDP, is expected to be positively correlated with consumption since it implies greater access to financial markets. Given that loan approval tends to depend on the ability of the prospective borrower to pay loan principal and interest out of current income, access to funds tends to be decreasing in the level of nominal interest rates, and nominal interest rates are expected to be negatively correlated with consumption (Wilcox 1989).[2] If establishing credibility or sufficiency of collateral are the issue, then the proportion of young people in the work-force (such as the proportion of the work-force aged between 20 and 29) may also proxy the shadow price and be negatively correlated with consumption.
If either financial repression or insufficiency of collateral is the source of the constraint, real asset prices (such as real residential property prices and share prices) and real income growth should be correlated with the liquidity constraint: an increase in real asset prices or real income eases the bind of the constraint, allows consumption to be brought forward, and current consumption rises. To the extent that constraints are binding and consumption cannot be brought forward, a rise in real income must increase current consumption, and so the excess sensitivity of consumption to income will occur generally when there is a constraint. The proxy variables outlined above and the expected effect of an increase in them on consumption growth are summarised in Table 2.
| Liquidity constraint | Expected effect on consumption |
|---|---|
| 1. Real consumer credit growth | positive |
| 2. Money market-deposit spread | negative |
| 3. Loan-deposit spread | negative |
| 4. Financial depth (M/GDP) | positive |
| 5. Nominal interest rate | negative |
| 6. Pop'n 20–29/pop'n 20–64 | negative |
| 7. Real asset prices | positive |
| 8. Real per capita income growth | positive |
The downside in this testing procedure is that since the proxies are not derived from first principles, their selection is relatively ad hoc. But the key test of validity in this case is that they be signed as expected if statistically significant. On the upside, the testing procedure has some strong advantages. It is broader than the simple excess-sensitivity test (in which consumption growth is just regressed on income growth) and provides a way to explicitly discriminate, albeit crudely, between financial market repression and other causes of liquidity constraints. The significance of real credit growth, interest rate spreads or financial depth, for example, implies that official controls or inadequate financial development generate the constraint, which can be remedied by liberalisation or implementing policies to develop financial markets. The significance of the nominal interest rate or share of young workers, on the other hand, points not to official controls or the under-development of financial markets, but to a constraint which arises out of the operation of capital and labour markets in general (although it is less clear what sort of policy should follow when this is the case).
In the estimations, this ad hoc specification is augmented by an error-correction term[3] which is included for a number of reasons. Firstly, the Euler equation predicts that variables dated t−1 and earlier do not contain information about current consumption growth and should be statistically insignificant when included in the estimating equation, with the variables included in this case being the first lag of real per capita income and consumption. This is not particularly persuasive, however, since aggregation across households has the effect that predictions based on an individual Euler equation do not generally follow through to the aggregate Euler equation when households are not infinitely lived (Gali 1990, 1991; Clarida 1991; Deaton 1992, pp. 37–43, pp. 167–176; and Muellbauer and Lattimore 1994, pp. 272–273). Even though labour income and consumption are not cointegrated at the individual household level, they will be at the aggregate level (Deaton 1992, p. 170). Moreover, if households are liquidity constrained, then their consumption is forced to follow the path of their income, so that if income is a non-stationary process, consumption will also be non-stationary and cointegrated with income (Blinder and Deaton 1985). Including an unrestricted error-correction term is a further way of testing the existence of liquidity constraints, although given the problem of aggregation, interpretation is not unambiguous.
The final issue concerns data definitions. Based on the theory, income should be defined as disposable labour income, but this definition is not generally available for the countries in this sample. The income variable for each country is defined in Appendix A, and varies from household disposable income (Australia, Japan and Thailand), factor income (Korea and Taiwan) and GDP (Hong Kong and Singapore). It is well understood that consumption, which is the object of intertemporal optimisation, is not necessarily the same as expenditure, which is the subject of statistical collection. Accordingly, time-series studies generally use data on sub-sets of consumption – either expenditure on non-durables or (most commonly) on both non-durables and services – or on the full set of consumption calculated as the sum of expenditure on non-durables and services and the estimated services flow from the stock of durables. Other papers use total private expenditure as a proxy of consumption. In this paper, results are reported for consumption measured as expenditure on non-durables, defined as food, beverages, tobacco and clothing. This measure is coincident with consumption, at least on an annual basis, and so is consistent with the theoretical derivation (assuming that welfare is separable between non-durables, services and the services flow from durables). Using non-durable expenditure ensures, firstly, that consumption is additively separable, and so the marginal rate of substitution between consumption in non-contiguous time periods is irrelevant, and, secondly, that difficulties associated with modelling adjustment costs do not arise (Deaton 1992). Expenditure on non-durables, as opposed to non-durables and services, is used as the base case for testing liquidity constraints since services expenditure may be contaminated by adjustment costs, time-series extrapolation or long-term welfare effects which render it non-additively separable even on an annual basis.
It is appropriate to ask what information non-durables expenditure contains about liquidity constraints. Common sense suggests that households do not generally use domestic and international credit markets to borrow to buy a jar of Vegemite or whatever, but do so to buy a car, household durables or a home, and so a better test of the evolution of liquidity constraints may be whether durables expenditure has become less sensitive to income (Takahashi and Kitamura 1993). The microeconomics of durables expenditure is, however, different to that of durables consumption and has to be addressed explicitly. Suffice to say that the objection is an exaggeration. If individuals do not face liquidity constraints, then it should be most obvious in the case of annual consumption of non-durable goods since issues of adjustment and time inseparability do not arise. Moreover, while expenditure on one item may be small, the bundle of total expenditure on non-durables is not (from an average 32 per cent in Japan to 58 per cent in Thailand) and credit markets, formal or informal, may facilitate these transactions. And, indeed, the existence of constraints on one class of expenditure, like durables, would be expected to spread to other groups of expenditure since saving to finance the former type of expenditure occurs at the expense of the latter.
Footnotes
An alternative derivation is the approach initially presented by Hall (1978) and developed by Campbell and Mankiw (1987, 1989, 1991), by which the population is bifurcated into a group which maximises consumption intertemporally and a group which are liquidity constrained. This is a special case of the model outlined in this paper when the shadow price on the liquidity constraint is proxied by current income growth. [1]
The nominal, rather than the real, interest rate is the proxy for the shadow price of borrowing. In the early literature on the real effects of financial reform, the real interest rate was often used as a proxy for repression (with a low rate indicating repression) (Fry 1995, p. 45). In this model, the real interest rate enters the equation as the opportunity cost of consumption. [2]
While lags of the first-difference of consumption and income are not included and the general-to-specific modelling strategy is not applied, this is not expected to have an effect on the results. In the first place, consumption and income appear to be random walks and so lagged first-differences are unlikely to have explanatory power. Furthermore, given the likely correlation of the proxy variables with the error term and the need for twice-lagged instruments, as discussed in Section 4, it is unlikely that past differences will enter the equation. [3]