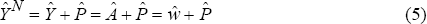RDP 9505: Labour-Productivity Growth and Relative Wages: 1978-1994 4. Wages and Productivity

One of the most frequently given explanations for the slowdown in aggregate productivity growth in the second half of the 1980s is that wages fell relative to the cost of capital and that this led firms to substitute labour for capital. Certainly after 1982/83, there was a significant decline in the share of GDP going to labour as real wages and real unit labour costs fell. Over recent times, analysis of the links between productivity and wages has often stopped with the observation that aggregate wage restraint led to a slower rate of increase in the capital-labour ratio and thus to slower labour-productivity growth. However, just as changes in output at the industry level can offer insights into the productivity issue, so too can sectoral changes in prices and wages.

The form of the links between wages, prices and productivity growth have long been debated in Australia. Discussion of the wage decisions made by the Commonwealth Conciliation and Arbitration Commission in the 1950s and 1960s was often centred on the relationship between average productivity growth and the increase in the aggregate nominal wage.^[22] At the industry level, analysis of the various linkages is made difficult by the fact that there is no dominant model in which to analyse outcomes. In general equilibrium, nominal wages (adjusted for skill differentials) should be the same in each industry. An increase in productivity, even if just in one industry, should lead to an increase in wages throughout the entire economy and, as a result, a change in relative prices and a reallocation of labour and capital. In practice, the labour market is rarely in equilibrium and changes in the level of productivity in one sector may influence both the sector's relative wage and the ability of the sector to attract resources from other parts of the economy.

The long time taken to re-establish equilibrium makes it difficult to formulate strong testable propositions. This difficulty is compounded by Australia's historically relatively centralised wage-fixation system, which created the possibility that, at least for a period of time, real wage increases were not directly tied to labour-productivity growth. This was particularly important in the 1980s. Over this period, real wages fell in a number of industries. This was not solely an outcome of the productivity performance of those sectors, but also reflected a decision by policy makers to achieve employment growth by reducing real wages; using the industry data, there is quite a strong negative correlation between productivity growth and growth in hours worked.

Even if the labour market was always in equilibrium, there are still no definitive predictions about changes in the sectoral allocation of labour and capital in response to productivity improvements in a particular sector. If one sector has an improvement in its technology, it may attract more workers and more capital, but it is also possible for that sector to lose both capital and labour. The loss of jobs in an industry undergoing relatively rapid productivity improvements is more likely if the underlying technical change is biased against labour, demand growth is weak and there are limited opportunities to substitute labour for capital. However, in general equilibrium, any labour made redundant by technological change is re-employed elsewhere in the economy in response to a change in relative factor costs. As discussed above, this equilibrium might be a long time in coming. A more difficult issue is what happens when technological change reduces the demand for a certain type of worker. If real wages for these workers fall, the level of employment in general equilibrium may well be lower if the new wage is below the workers' reservation wage.

In the following discussion an eclectic view is taken and it is argued that the evidence suggests that the links between wages and productivity have worked in both directions. Relatively high labour-productivity growth in some sectors has resulted in nominal wage increases in those sectors greater than average wage increases. In contrast, in other industries, the real wage restraint of the 1980s substantially reduced real product wages, and this allowed firms to take on more workers than would have otherwise been the case. On average, these workers produced less output than the existing workers and this reduced labour-productivity growth. This is particularly important in the recreation, personal and other services sector, and to a lesser extent in the wholesale and retail trade and construction sectors.

4.1 Productivity, Wages, Prices and the Mismeasurement of Output Growth

To discuss the relationship between measured productivity growth, wages and prices we start with a simple economy-wide production function. Real output, Y, is produced with capital, K, and labour, L, using the following constant returns to scale technology:

With fixed capital and labour, the rate of increase in real output equals the rate of technological progress:

where ˆ denotes percentage change.

The rate of increase in nominal output can be decomposed into the rate of increase in real output and prices. Further, if real wages increase at the same rate as real output, the following holds:

where P represents prices and w represents real wages.

Given that 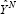is known, if the statistician underestimates 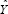, then the rate of price increase is overstated. In the extreme case, if technological progress is occurring but is assumed to be zero, the increase in nominal output is treated as inflation. It also means that measured real wages growth is zero, when in fact real wages are increasing.

We now move to partial equilibrium, assuming that labour does not move, or at least moves slowly, between sectors. In this case, an industry with relatively fast productivity growth should experience an increase in its relative nominal wage (because the relative marginal product of labour has increased) and a reduction in the relative price of its output (because relative marginal cost has declined). Therefore:

where W denotes the nominal wage and subscript i represents industry i.

This relationship implies that in the industry with relatively fast productivity growth, not only does the nominal wage increase relatively quickly, but so too does the relative product wage. Now consider what happens when the statistician incorrectly assumes that there is zero productivity growth in this industry. In this case, the increase in nominal output is interpreted as an increase in price, and thus the following relationships may apply:

While the nominal wage in the high-productivity-growth industry is still likely to increase faster than in the economy as a whole, the same is now also true for prices, so that the real product wage in the industry increases by a smaller amount than when there are no measurement problems. In the extreme case, if all sectors suffered the same measurement problems, those sectors with the fastest productivity growth would experience increases, rather than decreases, in their relative prices. Thus changes in relative prices and real product wages may give misleading signals as to relative rates of productivity growth. On the other hand, changes in nominal wages are likely to be subject to fewer measurement problems and, as a result, the behaviour of nominal wages might help provide insight into productivity outcomes at the industry level.

Suppose a sector shows negative productivity growth and a relatively fast increase in its implicit price deflator, but also a relatively large increase in its relative wage and its share of the economy's resources. This suggests that productivity growth in the sector is being mismeasured – a low-productivity-growth sector should not be able to attract an increasing share of resources and at the same time, pay those resources more than they are being paid elsewhere.

This analysis assumes that wages are determined by the marginal product of labour and that marginal products are not quickly equalised across sectors. Both assumptions are subject to question. If wages are set exogenously (at least for a period of time) and the economy is at less than full employment, a decline in real product wages will generate increased employment. Unless there is an improvement in technology, this increased employment will cause a decline in labour-productivity growth (that is, there will be a movement along the demand curve as opposed to a technology-induced shift of the curve). The other caveat is that in general equilibrium, nominal wages (adjusted for skill) in all sectors increase at the same rate, irrespective of industry productivity performance. Despite these qualifications, data on nominal wages may be useful in interpreting the industry productivity outcomes.

4.2 Productivity and Relative Nominal Wages

We now turn to the data on sectoral relative earnings and productivity growth. We have data on average weekly earnings of managerial and non-managerial workers in each of the 11 sectors. Figure 14 shows the relationship between labour-productivity growth and the change in relative earnings. The vertical axis shows the change in the log of labour productivity between March 1978 and June 1994; the faster an industry's productivity growth, the higher is the industry on the vertical scale. The horizontal axis shows, for the same period, the change in the ratio of average weekly earnings in the sector to economy-wide average weekly earnings; industries to the right of the vertical line at zero have experienced larger than average percentage increases in earnings. The top panel uses earnings of managerial workers and the bottom panel uses earnings of non-managerial wages.^[23]

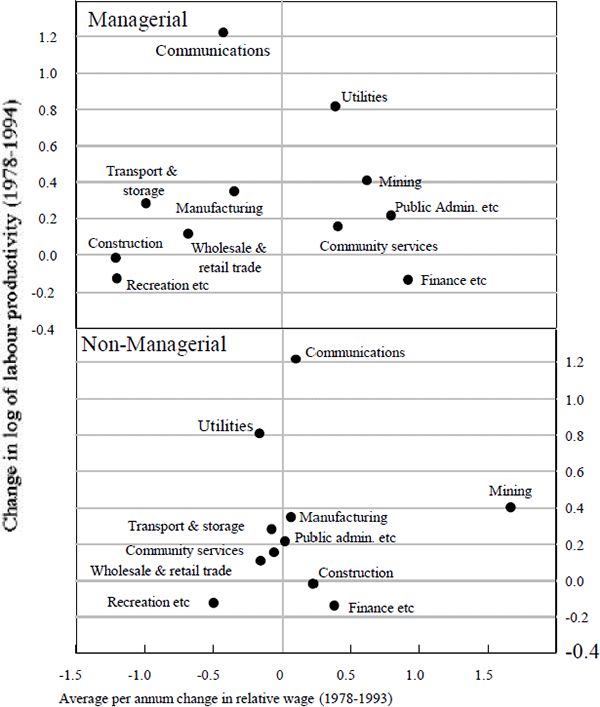
If relatively fast labour-productivity growth in one sector leads to an increase in the relative nominal earnings paid in that sector, the observations in these graphs should lie around an upward sloping line. While the relationship between relative productivity growth and relative earnings is quite weak, it does appear that in the wholesale and retail trade and recreation, personal and other services sectors, relative earnings for both managerial and non-managerial workers have declined.^[24] In contrast, workers in the high-productivity-growth mining sector experienced increases in their relative earnings. The data also suggest that in the utilities industry, the high productivity growth has been reflected in the wages of managerial workers, but not in the wages of the non-managerial workers. One possible explanation of this difference is that the technological change that has taken place in this industry is biased against relatively unskilled labour. It is also possible that the rather weak relationship between relative wages and relative labour productivity growth may reflect the fact that the 16-year time period is long enough for the general equilibrium results to establish themselves.

The finance, property and business services industry appears to be an outlier. Non-managerial workers in this industry have gained larger increases in earnings than workers in any other industry, with the exception of the mining industry. Further, the increases paid to managerial workers were the highest in any sector. At the same time that the finance sector was paying relatively large wage increases it was increasing its share of total hours worked; the share rose from 8.2 per cent in March 1978 to 12.7 per cent in June 1994.

Despite these changes, the data show a fall in the level of labour productivity in the finance sector over this 16 year period. Even if we abstract from the problems caused by the differences in the Survey of Employment and Earnings and the Labour Force Survey, measured labour-productivity growth in the industry was essentially zero. As the above discussion indicated, it is difficult to reconcile zero productivity growth with rising relative wages and a rising employment share. This suggests that the assumption of zero labour-productivity growth in the finance industry is inappropriate. In fact, the increasing relative wages in this sector is suggestive of substantial productivity improvement.

4.3 Productivity and Real Product Wages

Employment decisions are made on the basis of real product wages not real consumption wages. Over long periods of time the price deflators in different industries can move quite differently. Over the period from 1978/79 to 1992/93, the average annual increase in the implicit price deflator for the mining industry was 4.2 per cent, while the deflators for the recreation, personal and other services and finance, property and business services industries increased at annual rates of over 8.5 per cent. Such differences, cumulated over a long period of time can make large differences to the real product wages paid in the various sectors of the economy. Provided there are no measurement problems, sectors that experience relatively rapid productivity growth should experience increases in their real product wages, as the productivity improvements tend to put upward pressure on the sector's nominal wage and downward pressure on the price of the sector's output. Conversely, sectors with relatively low productivity growth should have declining product wages. As discussed above, this can also occur when there is excess supply in the labour market; in this case declining product wages ‘cause’ a decline in productivity by allowing less productive labour to be employed.^[25]

Figure 15 is similar to Figure 14 but now the horizontal axis shows the percentage change in real product wages over the period 1978 to 1993. Here, the observations tend to lie much more clearly around an upward sloping line. This implies that the faster is a sector's labour-productivity growth, relative to the economy as whole, the larger is the increase in the sector's real product wage. That is, differences in productivity growth tend to show up in relative prices, rather than relative wages. This positive (negative) correlation between productivity growth and real product wages (relative prices) is an enduring one. In examining wage and price outcomes in Australian manufacturing in the 1950s, Whitehead (1963, p. 189) found that approximately 70 per cent of changes in relative prices were associated with differential productivity movements. A similar conclusion was reached by Salter (1960) is his study of UK manufacturing.

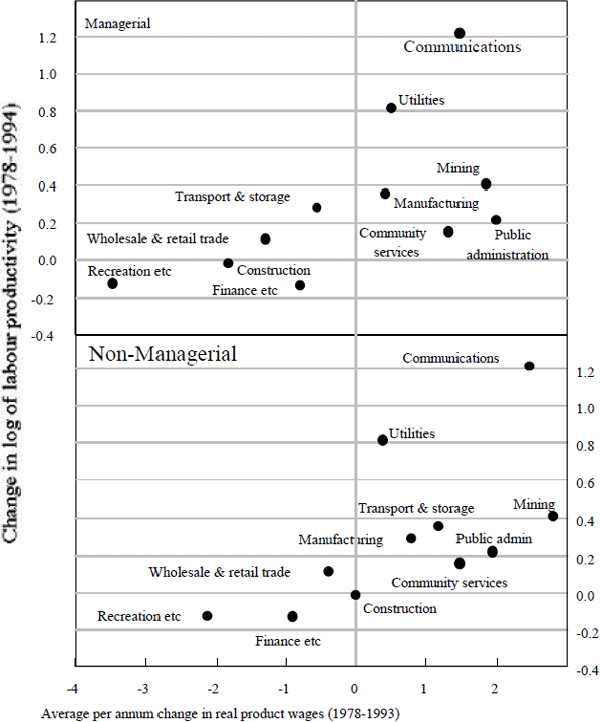
This positive association between productivity growth and real product wages it well illustrated by the recreation, personal and other services sector; it experienced the poorest productivity performance and it has also experienced the largest decline in its product wage. This decline reflects both relatively low nominal wage increases and a relatively rapid increase in the sector's price deflator. Apart from the difficulty of capturing changes in the quality of service provided, the measurement of real output in this sector is not plagued with serious problems. The low nominal wage increases suggest that the sector's overall productivity performance has indeed been relatively poor and, as a result, the relative price of the sector's output has increased. A similar picture emerges for the construction and the wholesale and retail trade sectors.

Together, wholesale and retail trade and recreation, personal and other services accounted for 31 per cent of the additional hours worked between March 1983 and December 1989. Workers in these industries tend, on average, to be less highly skilled than workers in the economy as a whole, and have weaker job tenure. Through holding down their real wages and allowing greater flexibility in work arrangements, firms found it profitable to take on workers, even though there was relatively little productivity growth in these sectors. Almost by definition, these new workers had lower levels of labour productivity than the existing workers, as firms were only willing to employ them at lower real product wages. In simple terms, a reduction in relative product wages was required to generate the jobs in sectors in which productivity growth was less than average; this reduction was brought about through wage restraint, but an increase in the relative price of the sectors' output also played an important role.

Measured real product wages have also fallen in finance, property and business services, but unlike the recreation sector, relative nominal wages have risen. The fall in product wages in this sector, is driven solely by the increase in the relative price of the sector's output. As discussed above, if a sector experiences productivity growth, but no growth is recorded, the measured price of the sector's output will increase. This appears to be what has happened in the finance industry, particularly in the period following the deregulation of the financial system. To a large extent, the increasing relative nominal wages in the sector reflect productivity growth, but this increase in wages is offset by an overstated increase in the price of the sector's output. The problems induced by this distortion are likely to increase through time, as the finance, property and business service sector is accounting for an increasing share of hours worked.

Footnotes

See the debate between Russell (1965) and Whitehead (1963, 1966). I am indebted to Glenn Withers for this historical perspective. [22]

For managerial workers, the 1978 observations are for private-sector, full-time male workers. The 1993, observations are for total (private and government), full-time male workers. For non-managerial workers the data for both time periods are for total (private and government) full-time workers. The data are from ABS Cat. Nos 6304.0 and 6305.0. [23]

The growth of part-time employment in these industries also has a role to play in explaining relative changes in average weekly earnings. More generally, changes in the relative education and skill levels of workers in different industries may influence the relationship between productivity growth and wages as well. [24]

This discussion ignores the impact of demand-side factors on product wages. This reflects the notion that an increase in demand should not permanently affect wages and prices, independently of its impact on the supply side; if marginal cost is constant, higher demand might drive up prices temporarily, but competition should eventually bid away any excess returns. There is, however, a role for the demand side to have a permanent effect of prices if the industry is subject to diminishing returns; if higher demand draws in more resources and reduces the marginal product then relative prices may increase. [25]