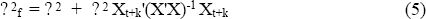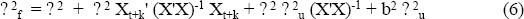RDP 9503: Monetary Policy Goals for Inflation in Australia 3. Issues In Formulating An Inflation Objective
March 1995
- Download the Paper 86KB
There are several key issues which need to be canvassed in formulating a robust and credible medium-term objective for inflation. We take up three of interest to us below.
3.1 What is the Appropriate Mean Inflation Rate?
What rate of inflation is, in Chairman Greenspan's words, sufficiently low that it does not “materially enter business and household financial decisions”?
Opinions on this seem to divide into those who accept that a low single digit inflation rate more or less amounts to “price stability”, and those who argue that 0.0 is a unique number – in Milton Friedman's words “a Schelling point – a natural point at which people tend to agree”.[3]
Konieczny (1994) takes the latter view. Amongst the arguments used here is the idea that only zero can be a credible target, because any other number leaves too much room for suspicion that a higher number will be adopted the first time the target is tested.
Others have taken a more cautious attitude. Apart from potential difficulties with targeting a zero CPI increase because of likely overstatement of the true rate of inflation by the measured CPI, this caution reflects concerns about perceived nominal rigidities which may impinge on real economic outcomes at crucial times. Fischer (1994), Summers (1991) and Corden (1994), amongst others, argue that such rigidities are sufficient reason to pursue a small single-digit inflation rate rather than “absolute zero”. Arguments that the short-run Phillips curve is very flat near zero inflation, so that lowering inflation the last couple of percentage points is increasingly costly, rely on similar ideas.
Some of the elements of these arguments are familiar. If there are downward rigidities in the setting of prices and wages, a small positive rate of inflation may facilitate the necessary adjustments of relative prices or wages. A real wage reduction may be more easily achieved by allowing nominal wages to fall behind inflation, than by an outright fall in nominal wages. Similarly, a firm may be reluctant to cut the nominal price of its product, but might accept a relative decline in its price as the prices of other goods or services grow faster.
This argument assumes that the face value of wages matters to workers as well as the real purchasing power of those wages, a kind of money illusion. Evidence of this has been found in practice (see, for example, Kahneman, Knetsch and Thaler (1986)).[4] It may be argued that this results from the experience of a protracted period of high inflation, where nominal wage rises were the norm, so that the expectation of wage increases would fade in a low inflation environment. An alternative explanation is that the downward rigidity of wages may be due to the motivational aspects associated with the nominal wage and concepts of wage fairness (see Solow (1979)), such that a nominal wage cut may have a negative impact on productivity.
These arguments appear to ignore productivity growth. If productivity is rising, workers can take cuts in their real product wage relative to their marginal product without taking a nominal wage cut. This would mean that nominal wage rigidity is not a good reason to eschew zero price inflation. This still leaves the feasibility of zero inflation as a function of productivity performance, however, and of the distribution of sectoral shocks. The problem of nominal rigidity may well be most acute in sectors which are performing badly, where a fall in relative prices and/or wages is appropriate, but which may also be characterised by low productivity growth.
If downward nominal rigidity in prices does exist, then the distribution of price changes when inflation is low should be truncated at zero. Despite a common assumption of nominal rigidities of this nature, the characteristics of price distributions have not been widely studied in Australia. However, a recent study by de Abreu Lourenco and Gruen (1995), using disaggregated data on producer prices, finds no evidence for truncation of the distribution of price changes at zero over the past 20 years. Whether this result extends to consumer prices has not been examined, and wage data in Australia are not sufficiently disaggregated to examine the distribution of wage changes.
A different nominal rigidity is the fact that nominal interest rates are typically bounded at zero. Summers (1991) has argued that a strict zero-inflation regime therefore removes the potential for negative real rates of interest, which might be appropriate at some times – for example, in the depths of a recession – to facilitate recovery. While the need for negative real rates may be infrequent, they could be very important in those rare cases, and arguably should not be ruled out by the adoption of a zero inflation rate target.
Critics of these views about nominal rigidities often respond by invoking the Lucas critique, arguing that nominal rigidities are themselves a result of the policy regime which has produced high inflation, and that they could be expected to diminish in importance as inflation falls to zero. Konieczny (1994) is a case in point. In the case of nominal wages, however, downward rigidity has been a persistent theme in macroeconomic debate even under regimes in which sustained periods of rising prices had not been experienced. This issue was at the heart of the debates of the 1920s and 1930s. The point about nominal interest rates being bounded at zero is also reminiscent of the debates about the “liquidity trap” of that era.
In our view, however, by far the most important fact is that no country has achieved absolute price stability in the past 50 years, and even achievement of low positive inflation over long periods has been quite rare, so our knowledge of empirical behaviour of modern economies in the region of zero inflation is scant. The longest period of relatively stable low inflation in recent history occurred in Germany from 1954–71 when average inflation was 2.3 per cent with a standard deviation of less than 1 per cent. That is, inflation lay within a 2 percentage point band about two-thirds of the time.[5]
A measure of caution is therefore appropriate. It is a persuasive enough argument in our view that high single-digit inflation rates (or something higher) do matter materially for long-run economic performance. The difference between 2 or 3 per cent inflation on average and something only slightly lower may be non-zero, but it is hard to believe it is quite so crucial. Given that there are costs to reducing inflation further, and that the size of the additional gains is less certain, a practical course, for the time being, in Australia is to direct policy towards maintaining the current low but still positive rates of inflation.
We doubt that this will be the last word on the subject. Success of the present policy strategy in securing some years of experience with quite low inflation, and the experience of other countries in pursuing inflation targets of various kinds, would leave us better equipped to decide on the merits of further efforts towards absolute price stability.
3.2 Variation Around the Mean
Since monetary policy operates on inflation with a lag, probably quite a substantial lag, policy makers must rely on their assessment of the likely future course of inflation in making adjustments to their instruments. But while everyone accepts that it is no use waiting for inflation to rise before responding with changes in the settings of monetary policy instruments, how good are we at forecasting inflation? And how sure are we of the responsiveness of inflation to changes in the instrument?
To formalise this a little, suppose the inflation process is generated as follows:
where X is a vector of explanatory variables (including the instruments of monetary policy), and ? a random disturbance with mean zero and variance ?2.
The central bank has a model of the inflation process:
where b is its estimate of ?.
The central bank wants to run policy according to an inflation target. While it hopes that ex post inflation will be kept within a certain band, its specific operational task is to adjust its policy instrument so as to keep its expectation of inflation at a relevant future date, t+k, within the band:
where L and U have the obvious interpretation. The central bank's forecast of inflation is:
If Xt+k were known, under the standard assumptions for the classical linear regression model the variance of the prediction error would be a combination of the true error variance and the variance of the linear predictor b:
Since the Xt+k are not known, however, but forecast, the variance of the inflation prediction error will be larger than this. It will be a (non-linear) combination of the variance of the parameter estimates in b, the variance of the error term ?, and the variance of the prediction errors for X (themselves a function of the variances of the relevant parameters and errors in the process generating forecasts of X). If X is a single variable, the standard result for the relevant variance is:
where ?2u is the variance of the error in the process generating forecasts for X (Pindyck and Rubinfeld (1991), chapter 8). (We will not attempt to write down the expression where X is a vector.) All of this assumes that the errors in the forecasting process for X are uncorrelated with those in forecasting ?, which is quite a strong assumption.
In other words, the fact that there is a stochastic element to the price generating process, that the structure of the economy (including its responsiveness to monetary policy) is not known with certainty, and that forecasts for inflation depend on forecasts for a range of other variables, themselves subject to error, all mean that the central bank's forecast for inflation has a confidence interval surrounding it which could well be relatively large.
Examination of models of the inflationary process are a start to gauging the size of this confidence interval. The price equation shown in part 4 of this paper has a standard error of about 0.3 per cent on a quarterly basis, which is fairly typical of price equations in Australia. This model has a 95 per cent confidence interval of about 1.2 percentage points either side of a central forecast of a four-quarter-ended inflation rate over a one to two-year horizon, on the assumption that future values of the regressors are known. Allowing for the fact that the right-hand-side variables in such an equation – labour costs, world prices for traded goods, exchange rates, output gaps and so on – must themselves be forecast, the size of confidence intervals must actually be bigger.
An examination of the forecasting record supports the contention that forecasts have a fairly large margin of uncertainty around them. In Australia, the Federal Government publishes a set of economic assumptions/forecasts with its annual Budget, based on the deliberations of a committee of officials from the Treasury and other Departments as well as the Reserve Bank. Surveys of private sector forecasters are also compiled. Annual forecasts and outcomes are shown below for the past decade.
| year to June |
Official forecast# |
Private sector “consensus” |
Outcome Headline CPI |
Outcome+ (adjusted) |
|---|---|---|---|---|
| 1985 | 5.25 | n.a. | 6.6 | 6.6 |
| 1986 | 8.0 | 8.4 | 8.5 | 8.5 |
| 1987 | 7.5 | 8.4 | 9.3 | 9.2 |
| 1988 | 6.0 | 6.8 | 7.1 | 7.4 |
| 1989 | 4.5 | 5.1 | 7.6 | 6.5 |
| 1990 | 7.0 | 7.6 | 7.7 | 6.5 |
| 1991 | 6.0 | 6.9 | 3.4 | 4.3 |
| 1992 | 3.75 | 4.1 | 1.2 | 2.7 |
| 1993 | 3.0 | 2.7 | 1.9 | 2.8 |
| 1994 | 3.5 | 2.8 | 1.7 | 2.3 |
| mean error (π$−π) |
−0.23 |
0.29 |
||
| RMSE | 1.27 | 1.21 | ||
# Announced in August of preceding year. |
||||
There is a slight tendency for official forecasts to underestimate inflation on average over this period, while the reverse is true for the private forecasters. Neither of these is statistically significant. The pattern of errors is quite similar, with both sets of forecasts underestimating inflation in the late 1980s, then seriously missing the big fall in inflation in 1991 and 1992, and subsequently tending to be too pessimistic about the prospects for inflation remaining low. The root-mean-square error of both sets of forecasts is of the order of 1¼ per cent.[6] This is only slightly below what would have been achieved by a naive “no change” forecasting rule.
There is a considerable international literature on the issue of forecasting accuracy which there is no space to review here. For the purpose at hand, however, it is sobering to note that this (admittedly quite rudimentary) analysis suggests that the 95 per cent confidence interval around a central inflation forecast over one year – a period during which monetary policy is unlikely to be able to alter the path of inflation very easily – is of the order of ±2.5 percentage points! It is also worth noting that the above results for Australian forecasts appear to be comparable to those quoted by the OECD (1993) in a study of their own forecasts for G7 countries.[7]
This potentially poses something of a dilemma for the policy makers in announcing a target band. On the one hand, the genuine difficulties in forecasting and controlling short-term movements in inflation suggest a fairly wide band. On the other hand, a band wide enough to encompass all these uncertainties may be so wide as to lack credibility.
There are, of course, reasons to believe that the previous forecasting record will give an overestimate of the relevant confidence interval for forecasts associated with the operation of an inflation target. One is that such forecasts often did not assume, at least not explicitly, that shifts in economic policy settings would take place. In Australia, they have usually also been prepared on the technical assumption that the exchange rate would not change, whereas the Australian dollar has at times shifted substantially during the interval between a forecast being made and the result being observed (at times because of policy changes, and other times provoking policy changes). To the extent that the forecasting process and the policy-adjustment process could be made truly a joint one – as they should be in a strict inflation targeting regime – policy-related factors bearing on inflation (including through the exchange rate) might be incorporated more effectively in forecasts and improve their accuracy (although this would present considerable difficulties for making details of those forecasts public).
3.3 Response to Shocks
A further reason for large ex post errors in some years will have been genuine shocks of the kind that no policy regime can cope with easily. Even with good forecasts, shocks – by definition unanticipated – will occur which push inflation out of the target band ex post, even though the central bank's unbiased expectation was that inflation would be in the centre of the band. In this situation, how quickly should the central bank try to return to its preferred inflation range? This is, in practice, one of the key operational considerations for policy.
The answer to this question will depend to a large extent on the nature of the shock. In the case where demand, rather than supply, shocks are prevalent there may be relatively little real conflict between the price and output objectives. In a conventional macro model, positive demand shocks push output away from its “natural” level, open an output gap, leading to pressure on inflation (probably with some lag) and raising the equilibrium interest rate. A policy framework which proceeds by adjusting interest rates according to movements in the output gap should also assist in stabilising prices, assuming the regime is sufficiently credible that the demand shocks themselves do not de-stabilise price expectations unduly. It is this world to which an inflation target seems ideally suited.
Where supply shocks occur, on the other hand, monetary policy can only dampen price variability by adding to short-term output variability, so there is a short-term conflict between the two objectives, and a multi-faceted objective function leaves the policy maker with difficult choices. Even if primacy is given to restoring price stability, there are still decisions to be made about the nature of the adjustment path that is to be sought.
Here the slope of the short-run Phillips curve (and potential non-linearities in it), the extent to which inflation affects long-run growth potential, and the responsiveness of inflationary expectations to short-term movements in actual inflation all figure in an assessment of how to respond to the shock.
It is presumably because of this possibility that some of the inflation targets which are in operation have specific “escape clauses” which permit the central bank, in effect, to receive a new set of instructions from the government in the event of a major supply-side shock. Even if the shocks can be assessed in an accurate and timely fashion, and an appropriate adjustment to policy implemented, there will still be questions about the possible effects on the credibility of the policy regime of tolerating a temporary departure from the inflation objective.
In establishing any sort of public objective for inflation, then, a key question is what variance of inflation can reasonably be expected to be achieved, given what we know about the nature of the shocks to which the economy is typically subject. While major, identifiable, supply-side shocks may be a sufficient condition for the suspension of a target, the regime needs to be sufficiently robust to handle more minor shocks of various kinds without being re-cast often; otherwise there will be potential loss of credibility.
In terms of the stylised model above, there will be an irreducible variance in inflation over time which is a function of the various genuine stochastic processes in the model and the model's dynamics (even leaving aside uncertainty about the model's structure). This minimum variance of inflation might not, furthermore, be “optimal” if there are other considerations for the policy-maker – for example, if the variance of output relative to potential is an objective in its own right.
In principle, there will be a schedule relating output variance to inflation variance, for given characteristics of the various shocks, traced out by the different weights on those two variables in the policy reaction function of the central bank – a trade-off of the kind outlined by Taylor (1992). Policy-makers must make their value judgement about what point to choose on this frontier (noting as they do so that, in the best tradition of trade-offs in economics, some short-term choices may cause the nature of the trade-off to shift over time). In the following section, we make a preliminary attempt at examining empirically some of these issues for Australia.
Footnotes
Friedman (1985), quoted in Jack Selody (1990). [3]
Kahneman et al. also find that nominal wage cuts are acceptable when a firm is losing money or facing bankruptcy. [4]
See Lebow, Roberts and Stockton (1992), who provide a useful review of this history for the G7 economies. [5]
It is easy to make unfair criticisms of price forecasts given that official forecasts are prepared on a technical assumption that interest rates do not change, whereas the actual outcomes for the CPI almost always are affected by rate changes. In the above, we “back out” these effects from the outcomes in order to provide a more useful comparison between outcomes and forecasts. It is less clear whether private forecasters, who are not constrained to make the same assumption, should benefit from the same adjustment. [6]
The weighted average RMSE of the individual OECD forecasts for the G7 countries over the period 1974–1992 was 1.5 per cent. This result is pushed up by one very large error – the OPEC I inflation of 1974 – and results for later periods are better. Even so, the RMSE's for the individual country forecasts amongst the G7 range from around 0.5 to around 1.5 per cent for the period 1987–92. [7]