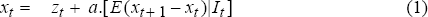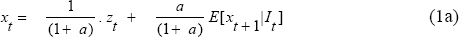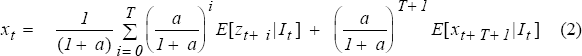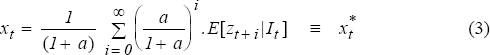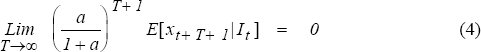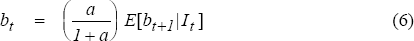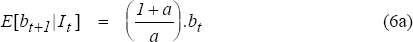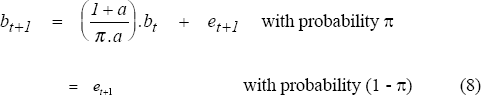RDP 9501: Modern Approaches to Asset Price Formation: A Survey of Recent Theoretical Literature 2. Rational Bubbles

2.1 Theoretical Development

The theory of “rational bubbles” represents one important strand of the literature that has developed to explain divergences of asset prices from their fundamental or intrinsic values. It was the academic community's first attempt to rigorously challenge key propositions of the EMH. It demonstrates that, even with rational expectations and behaviour, “rational” deviations in asset prices from their intrinsic values – a rational bubble – would be possible.^[8]

Simply stated, a rational bubble is present whenever an asset price deviates progressively more quickly from the path dictated by its economic fundamentals. The growth of rational bubbles reflects the presence of arbitrary and self-confirming expectations about future increases in an asset's price. They would be a feature of a market in which an investor purchases an asset solely in anticipation that it could be resold at a higher price to another investor willing to purchase the asset for the same reason. Thus, an explosive divergence from fundamentals would be possible even if economic agents always held rational expectations and rational arbitrage conditions were satisfied.

The potential for rational speculative bubbles exists in the large class of dynamic asset pricing models, in which the equilibrium price in the current period depends on expectations about future changes in the asset's price. In these models, such bubbles can emerge if expectations are rational and the current equilibrium price depends positively on its own expected rate of change.

These models of rational speculative bubbles are indeterminate. In other words, they have an infinite number of equilibrium solutions. The indeterminacy comes about because asset pricing models with such a structure essentially possess only one condition to constrain asset market equilibrium and rationality of expectations, whereas the model's solution dictates solving for two endogenous variables – the current equilibrium asset price and its expected rate of change – in each period.^[9] Thus, in these models, there can exist a multiplicity of asset price solutions or trajectories, of which only one corresponds to the economic fundamentals; the other trajectories will all contain asset price bubbles.

To see most simply how rational bubbles can arise, consider the following asset price expression:^[10]

where x_t is the (logarithm) of the equilibrium asset price at time t; zt represents a scalar measure of current period “fundamentals” affecting the asset price, i.e. the economic conditions of supply and demand; [E(x_t+1−x_t)|I_t] represents the expected percentage rate of change of the asset price between period t and t+1, conditional on all information currently available, I_t; and a is a positive constant representing the elasticity of the current asset price with respect to market expectations.

Equation (1) states that the spot asset price in any period is determined by the current period “fundamentals” and the prospective capital gain or loss from holding the asset until the next period. It embodies rational expectations, since the expectation is the mathematical expectation of the change in the asset price based on all information currently available.^[11]

Re-arranging equation (1) gives:

This is a stochastic difference equation in the asset price, with the fundamentals, z_t, acting as the “forcing” process. Applying the “law of iterated expectations”^[12], equation (1a) can be solved recursively forward T periods, yielding the following expression:

A particular solution to the stochastic difference equation (1a) is given by:

Equation (3) defines the fundamental or intrinsic value of the asset price at time t, denoted as 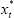. The fundamental spot price of the asset at time t is an exponentially weighted sum of present and expected future values (conditional on the information set available in period t) of all relevant economic fundamentals.

However, 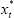is the unique solution to the difference equation (1a) if, and only if, the following condition is satisfied:

Condition (4), sometimes referred to as a transversality condition, is regularly assumed, though in most instances, there is no a priori justification for its imposition. If the transversality condition does not hold, then the stochastic difference equation (1a) has an infinite number of solutions of which only one corresponds to the fundamental solution .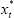

The general solution to the stochastic difference equation (1a) is given by a set of solutions of the form:

observed asset price = fundamental value + rational bubble

More precisely, each solution may be expressed as:

where 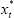is given by equation (3) above, and b_t satisfies the condition:

or equivalently,

The stochastic process b_t is defined as the rational bubble component of the asset price, and is simply the difference between the actual price at time t and its intrinsic value determined by prevailing economic fundamentals. Condition (6) above states that, for a bubble to be a viable outcome, it must reflect the expectation that it will continue to expand in the following period.^[13] If the transversality condition holds, then b_t = 0, which implies that the observed price corresponds with its long-term equilibrium value. Thus, a common theoretical interpretation of rational speculative bubbles is as a violation of the transversality condition.

2.2 Deterministic and Stochastic Bubbles

In its simplest (and least plausible) form, a rational bubble may follow a deterministic time path, with deviations from fundamentals growing exponentially. An example of such a deterministic or ever-expanding bubble is:

In equation (7), b₀ is an arbitrary non-zero constant. This equation implies that the asset price will diverge explosively forever from its intrinsic value – a highly improbable event.

Blanchard (1979) and Blanchard and Watson (1982) advanced a more realistic model. Referred to as rational stochastic bubbles, these have the feature of growing over a certain interval, before suddenly collapsing. The following stochastic process illustrates:

where the bubble “innovation” e_t+1 satisfies E[e_t+1|I_t] = 0

Under this formulation, there is a probability, π, that a bubble will survive until the next period and a probability, (1 – π), that it will crash in the current period. If the bubble crashes, the asset price will return to its intrinsic value. The “innovation” term e, implies that a bubble can regenerate itself after crashing; the stochastic bubble can thus burst and restart repeatedly.

This bubble structure can also be extended to allow for certain features that have been observed in speculative asset markets. Blanchard and Watson (1982) suggest that the specification of π, the probability of the bubble's survival, could be refined. It could, for example, have stochastic properties and be determined by such factors as the length of time the bubble has lasted, or the deviation in the asset price from its fundamental value. An alternative approach would be to model it as a function of fundamental variables, such as “news” about key economic aggregates.

2.3 Are Rational Bubbles Rational?

Blanchard and Watson conclude that the persistence of such stochastic bubbles remains compatible with the postulate of rational expectations. Although rational investors can be certain that a bubble will ultimately collapse, they will always be uncertain about the timing of any crash. Consequently, they may continue holding an asset in the hope of realising even larger capital gains from further rises in its value. At the beginning of each period, rational investors will decide whether to liquidate their positions, and take profits, or to continue holding their positions in anticipation that the bubble will survive and yield even larger (unrealised) capital gains. They will choose the latter course if they expect to be compensated – by a higher expected rate of growth in the asset price bubble – for taking the chance that the bubble will collapse. It is for this reason that the expected rate of growth of a stochastic rational bubble, if it survives, is greater than that of a deterministic rational bubble.^[14]

The extent to which such rational bubbles are truly consistent with rationality is an issue which has attracted considerable attention in the academic literature. Contributions by Tirole (1982, 1985) as well as Diba and Grossman (1987, 1988), identify conditions which would preclude the emergence of rational bubbles in dynamic asset pricing models. Tirole (1982) demonstrates that rational bubbles cannot develop when (i) the asset has a finite life, and hence a definite terminal value^[15] or (ii) if there exist a finite number of traders, who have rational expectations and optimise over an infinite horizon.^[16] Tirole (1985) shows that, in an overlapping generations framework, in which there exists an infinite succession of new (finite-horizon) traders coming into the market, rational bubbles can exist provided the economy is dynamically inefficient. By this, it is meant that the rate of growth of the economy exceeds the rate of interest. If this condition is violated, however, there will exist a point in time where the wealth of new asset holders will be insufficient to purchase the asset upon which a bubble has developed.

Diba and Grossman show that in such models, if a rational asset price bubble does not exist in period t, then it cannot get started in period t+1 nor in any other subsequent period. As a consequence they argue that, if a rational asset bubble exists, it must have started on the first day of trading.^[17] One implication of this is that a rational bubble could not restart once it had collapsed.

2.4 Intrinsic Bubbles

In the original formulation of rational speculative bubbles, the “bubble” component was completely divorced from the “fundamental” component, and was driven entirely by extraneous variables. Recent theoretical contributions by Froot and Obstfeld (1991) and Ikeda and Shibata (1992), however, re-examine the relationship between the bubble and fundamental components of dynamic asset pricing models.

Froot and Obstfeld (1991) demonstrate the possibility of a distinct class of rational bubbles which they refer to as “intrinsic bubbles”. Unlike the rational bubbles discussed above, intrinsic bubbles do not depend on arbitrary and extraneous factors, but instead are specified as being deterministic non-linear functions of the asset's fundamentals. This sort of bubble process has a number of properties which make it a more plausible description of the departure of asset prices from their intrinsic value. Specifically, in this class of model:

• departures from fundamental values can persist, and appear stable, for long periods of time, so that stable economic fundamentals can be associated with stable and persistent under/overvaluations of asset prices;
• asset prices can overreact to “news” about the fundamentals; and
• asset prices can converge to their fundamental value and then diverge, giving the appearance of periodically bursting and restarting.

Ikeda and Shibata (1992) also propose a bubble which depends on fundamentals but in which the economic fundamentals are stochastic; current fundamentals affect rational investors' expectations about market conditions and, hence, future asset prices. Ikeda and Shibata (1992) demonstrate that their “fundamentals-dependant bubbles” are qualitatively distinct in several respects from traditional models of rational bubbles. In particular, these bubbles may periodically contract and expand, and display monotonic declines in both magnitude and volatility. Furthermore, the sign of the bubble's correlation with the fundamentals varies over time. When this correlation is negative, the bubble-inclusive asset price displays less volatility than the asset's fundamental value.

While the theory of rational speculative bubbles provides one explanation of departures in asset prices from their fundamentals, it has some drawbacks. One significant deficiency is that the “microstructure” of the bubble process is seldom, if ever, specified. Both the inception and collapse of a rational bubble is taken as exogenous. Thus the conditions and mechanism by which such bubbles can be generated, and the events contributing to their sudden collapse, are not spelled out in any satisfactory way, if at all. Moreover, these models imply that there exists an infinite number of equilibrium price trajectories, only one of which is consistent with the economic fundamentals. The theoretical framework thus implies that an observed asset price will rarely correspond to its intrinsic value – for some, an unattractive characterisation of real-world asset price movements. As a consequence of these deficiencies, alternative theoretical frameworks have been developed, especially ones which relax the assumption that all investors and traders are rational. These models are covered in the next section.

Footnotes

Important contributions include those of Blanchard (1979), Blanchard and Watson (1982), Flood and Garber (1980) and Tirole (1982, 1985). For a detailed and more technical discussion see Chapter 5, Blanchard and Fischer (1989). [8]

See Flood and Garber (1980) and Flood and Hodrick (1990). [9]

Frenkel and Mussa (1985) argue that a diverse range of structural models of exchange rate determination can be subsumed under this reduced form asset-price expression. [10]

In addition to this assumption that the expectation is the mathematical expectation, two other assumptions are implicitly made in defining rational expectations. First, everyone possesses or observes the same “information set” at time t, i.e. I_t is common to all economic agents. Second, there is agreement among all economic agents as to what constitutes the underlying economic model, as well as full knowledge of its parameter values. [11]

Formally, if the information set I_t is a subset of the information set I_t+1 then E[E[x|I_t+1]|I_t] = E[x|I_t]. This basically states that the expected value today of next period's expectation of the random variable x, is the same as today's expectation of the same variable x. [12]

Note that projecting into the infinite future, the rational bubble component explodes in expected value:
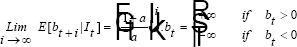[13]

Observe that 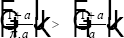[14]

To see this let T be the terminal date of the asset and 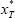its terminal value. In period T the price of the asset will be equal to its terminal value and hence no bubble will exist i.e. x_T = 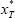⇒ b_T = 0. 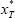However rational expectations dictate that if no bubble exists in period T, then none will exist in period T−1; rational investors will not pay more than the discounted terminal value of the asset, , in period T−1. Proceeding with a such a backward induction argument it logically follows that a rational bubble cannot exist in period T−2, nor in period T−3, nor in any other preceding period including period 0. That is to say, a rational bubble will never arise. [15]

This argument is based on a view that trading is a zero-sum game. From an aggregate perspective, the real worth of an asset is, by definition, equal to its fundamental value. In a market with a finite number of traders, some traders may be able to sell their asset holdings at bubble prices but the buyers will be worse-off. If investors who have sold at a price above fundamentals, then exit the market, remaining traders will be involved in a “negative-sum game”. Tirole argues that rational investors would recognise this problem, thereby ensuring that an asset price bubble would not emerge to begin with. [16]

Note that if b_t = 0 at some date t then from condition (6a) above it follows that E[b_t+1|I_t] = 0. However, with the assumption of “free disposal” (i.e. investors can always “walk away” from their investment in an asset) b_t+1 is a non-negative random variable i.e. b_t+1≥0. Therefore, from the above two propositions, it follows that if b_t = 0 then b_t+1 = 0 with probability one. [17]