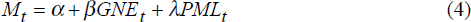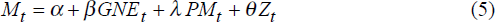RDP 9312: A Re-examination of the Determinants of Australia's Imports 5. Estimation of Demand for Imports
December 1993
- Download the Paper 70KB
Valid estimation requires that account be taken of the time series properties of the data to be employed. All data to be used in the estimation of import demand are non-stationary.[18] An approach to deal with non-stationary data that has been employed by recent contributors to the empirical literature on import demand combines the concepts of cointegration and error correction.[19] In this paper, the cointegrating relationship between import volumes and its explanators is tested and estimated using the Phillips and Hansen (1990) fully modified OLS estimator. The estimation period is from the September quarter 1974 to the March quarter 1993.
5.1 Aggregate Imports
We commence with estimation of the traditional import demand function for aggregate imports, estimated in log levels, where import demand is a function of economic activity and the relative price of importables:
Results from the P-H estimator confirm the existence of a cointegrating relationship (see Appendix 3). The long-run elasticity estimates are shown in Table 1, with the model denoted by the equation number.
| Model | Activity | Relative Prices | Protection |
|---|---|---|---|
| Traditional model: without tariff adjustment (3) |
1.55 (0.05) |
−0.42 (0.13) |
.. |
| Protection models: with landed import prices (4) |
1.50 (0.06) |
−0.41 (0.13) |
.. |
| with effective protection term (5) | 1.57 (0.07) |
−0.41 (0.13) |
−0.04 (0.49) |
| Note: Standard errors are shown in parentheses. | |||
The result is standard: the volume of imports is directly related to economic activity and inversely related to price. The sizes of the coefficients fall within the bounds of those reported in many other Australian studies.[20]
However, recently there has re-emerged a debate about the appropriate size of the income elasticity for imports.[21] In theoretical literature it is often claimed that, in the long run, the income elasticity should be unity. Formally, this assertion is based on assumptions of long-run steady state growth and the homothetic demand of identical consumers (Magee 1975). The intuition behind this assertion is that while the income elasticity may exceed unity in the short to medium term due changes in patterns of production or consumption, the effect of these changes will be dissipated so that, in the long run, there is a stable relationship between income and imports.[22] Subscribers to this theory would argue that the size of the income elasticity generated by the traditional model is too high and is the result of misspecification. Certainly, such concern is expressed by Bullock et al. (1993) with respect to reported income elasticities for Australia.[23]
In essence, the income elasticity generated by the traditional model tells us that the growth in import penetration we have observed is primarily attributable to the growth in income. However, the omission of relevant explanators will bias the income elasticity. Therefore, we approach the issue of possible mispecification by considering factors other than income.
First, we consider the use of additional relative prices. This approach is in keeping with the tradition of emphasising the role of price elasticities in the determination of trade volumes (Houthakker and Magee 1969, p.111). However, additional relative price terms do not emerge as being statistically significant (see Appendix 3). Instead, we attribute possible misspecification of the traditional import demand equation to the failure to account for changes in protection. Thus we move from the benchmark traditional model to one that includes protection.
There are two main ways in which protection can be included. The landed price of imports can be considered, with the effect of tariffs subsumed into the relative price term so that:
Alternatively, a measure of the effective rate of protection can be included as a separate argument so that:
Inclusion of the effective rate of protection as a separate argument is designed to capture factors in addition to the direct effect of changes in protection on the relative price of imports. That is, its purpose is to capture the indirect effects of the lowering of protection on import volumes, such as may be associated with changed conditions of domestic supply of importables.[24]
The results from these two approaches are also shown in Table 1. Note, that neither approach yields discernible evidence of a tariff effect. There is no clear fall in the income elasticity: in both cases, at the 5 per cent level, the income elasticity is not significantly different from that in the traditional model. There is no significant change in the price elasticities and the protection term, when included separately, is insignificant.
Standard theory says that changes in protection will alter relative prices and, thereby, import demand. The fact that the effects of protection are not channelled through the landed price term in equation (4) is, perhaps, surprising. However, as discussed in Section 2, the impact of changes in protection on the landed prices of imports is typically found to be small, because the bulk of any movement in such relative prices is most often explained by exchange rate fluctuations.[25] More interesting is the fact that in equation (5), the effective rate of protection – the term for openness – proved to be insignificant. Certainly, a priori reasoning would suggest that a regime shift in protection must impact upon import volumes. The question then arises, why is this not evident in the specification adopted here?
Magee (1975) acknowledges the difficulties of explaining import volumes for product areas in which imports have domestic substitutes. He shows analytically that import penetration will increase when the domestic demand elasticity for importables exceeds the domestic supply elasticity, or when shifts in demand for importables exceed those of supply. He argues that these rules of pure theory can be used to explain the ‘frustrating empirical problem’ of identifying excess demand for importables.
Magee's rules can be applied to demonstrate the apparent failure of changes in protection to explain aggregate import demand. For instance, adjustments of the domestic supply of importables to the dismantling of protection may be more gradual than changes in demand, making the influence of falls in protection difficult to establish statistically. Against the backdrop of secular change in the supply of import substitutes, there are big swings in the demand for imports that are associated with changes in activity and relative prices. In a statistical sense, the information contained in such swings in demand tends to dominate that afforded by the underlying structural changes in conditions of supply.[26]
Furthermore, imports are not a homogeneous bundle of goods. A model for aggregate imports may mask important differences in the effect of falling protection on the market for some categories of imports. In particular, it might be expected that the market for consumption imports has been most affected by lower protection whilst that for capital imports has been least affected.[27] It is proposed that a disaggregated approach will permit the influence of supply side effects of changes in protection to be identified. These possibilities are explored in the following section.
5.2 A Disaggregated Approach
We re-estimate equation (5) for imports of consumption, capital and intermediate goods. We use the prices that correspond to each class of import. However, we maintain the use of an aggregate measure of economic activity.[28] We argue that, in an excess demand formulation, when the activity variable is ‘finely tuned’ to correspond to a particular class of imports, its behaviour accords too closely with that of the dependent variable and, thereby, inhibits the identification of more gradual supply side change, such as may be associated with falls in protection.
The results obtained from the re-estimation of equation (5) with disaggregated data accord with priors better than the results obtained from the other models, including models which employ the ‘finely tuned’ disaggregated activity variables. A comparison of all models is provided in Appendix 3. A summary of results from the preferred model is presented in Table 2 for each class of import. They reveal some important differences in the response of components classes of imports to changes in activity, relative prices and protection.
| Model | Activity | Relative Prices | Protection |
|---|---|---|---|
| Protection model: | |||
| with effective protection term (5) | |||
| consumption | 1.48 (0.11) |
−0.78 (0.10) |
−1.59 (0.54) |
| intermediate | 1.22 (0.12) |
0.00 (0.15) |
−1.32 (0.59) |
| capital | 2.04 (0.27) |
−0.72 (0.24) |
3.02 (1.15) |
| Note: Standard errors are shown in parentheses. | |||
For imports of consumption goods, the term for protection has the expected sign, is significant and its inclusion is associated with a reduction in the income elasticity. Whilst the income elasticity is significantly lower, it nonetheless remains quite high. This class of import is more likely to have a higher income elasticity than others as it fits well the ‘desire for variety’ hypothesis. Use of disaggregated data also reveals that the relative price elasticity for consumption goods is significantly higher than for the models of aggregate imports in Table 1. This is consistent with the responsiveness of consumption decisions generally to changes in price, given the availability of substitutes.
For imports of intermediate goods, the term for protection also has the expected sign and is significant. Again, its inclusion is associated with a reduction in the income elasticity. In fact, the income elasticity for intermediate goods is notably lower than that for aggregate imports. Furthermore, in this case, the price elasticity is insignificantly different from zero.[29] This suggests that the decision to import an intermediate good (for which there are few domestic substitutes) will be related primarily to economic activity and not to relative prices. In fact, the lack of response of intermediate imports to changes in relative prices is a key factor explaining the size of the relative price elasticity for aggregate imports.[30]
It is of concern that for imports of capital goods the protection term is significant and of the wrong sign. Furthermore, its inclusion increases the income elasticity. Because capital imports have few domestic substitutes and have been subjected to generally lower levels of protection, it may be expected that changes in protection are less significant for capital than other classes of import. Nonetheless, a positive coefficient is perverse.
However, a role for protection that accords with our priors has been found for consumption and intermediate imports which, together, account for about 80 per cent of the nation's total endogenous imports. An important question is the extent to which reductions in protection have contributed to the growth in these classes of import. We focus on the impact of the fall in protection since its local peak in the March quarter 1984. Our preferred model is used to generate a long-run equilibrium volume of imports. An experiment is then conducted to predict the change in import volumes that would have occurred if the level of protection had remained fixed, with all other things changing. That is, we present the counterfactual.[31] The difference between this counterfactual level of import volumes and its true long-run equilibrium level permits identification of the contribution of the fall in protection to the growth in imports.[32] The results are summarised in Table 3 for each class of import.[33]
| Import Class | Consumption | Intermediate |
|---|---|---|
| Estimated long-run growth | 47.1 | 46.4 |
| Percentage point contributions: | ||
| Activity | 41.2 | 33.7 |
| Relative prices | −11.6 | 0.0 |
| Protection | 18.2 | 14.7 |
These results indicate that of the 47 per cent increase in consumption imports since the March quarter 1984, about 18 percentage points (or two fifths) are attributable to reductions in protection. The impact of falling protection has been less pronounced for intermediate imports, but is nonetheless substantial, with about 15 percentage points (or one third) of the increase due to falls in protection. Given that these categories, when combined, represent the bulk of the nation's imports, it is apparent that the dismantling of protection has been a major contributor to import growth. In fact, reductions in protection have been the largest contributor other than income to the growth in non-capital import volumes.
Footnotes
The time series properties of the data are reported in Appendix 2. [18]
Refer to Hall et al. (1989), Horton and Wilkinson (1989), Wilkinson (1992) and Bewley and Orden (1991). [19]
See Macfarlane (1979), Horton and Wilkinson (1989), Hall et al. (1989) and Bullock et al. (1993) for a discussion of elasticities. [20]
The early debate is most often associated with Houthakker and Magee (1969) who demonstrated the potential importance of high income elasticities with respect to secular trade imbalances. For a review of the recent debate see Blecker (1992). [21]
However, convincing arguments can also be made that the income elasticity may exceed unity if an allowance is made for, say, the ‘desire for variety’ at higher levels of income. Krugman (1989) offers a detailed discussion of factors determining income elasticities for imports. [22]
It may also be the case that the estimation periods in the various Australian studies do not permit identification of the true long-run relationship. However, the systematic tendency for traditional models to generate high income elasticities suggests that the problem is one of misspecification. [23]
The term for the effective rate of protection will also be capturing indirect demand effects to the extent that purchasers of imports respond to factors other than income and relative prices as protection is dismantled. In the framework adopted in this paper, it is not possible to distinguish between indirect demand and supply side effects. However, given the evidence of a structural change in the supply of import-competing goods presented in Section 2, our prior is that supply side effects will dominate. [24]
Even though a cointegration framework is designed to identify long-run relationships, it may be that, during the period of estimation, exchange rate fluctuations have been sufficiently large to obscure the impact of tariff reductions on the landed price of imports. In consequence, the choice of landed prices compared with those free on board makes little difference statistically when attempting to measure import demand. [25]
And, indeed, underlying changes in demand for imports that are independent of activity and relative prices. [26]
Generally, finished goods, for which there are domestic substitutes, have had the highest rates of protection and have experienced greater relative cuts in protection since 1984. Capital imports, on the other hand, have few domestically produced substitutes and typically have been afforded lower levels of protection (see Industry Commission, Annual Report, various years). [27]
Similarly, Phillips (1989) uses a general measure of activity when estimating disaggregated models of import demand. Alternatively, for each class of imports, Athukorala and Menon (1988) nominate a corresponding expenditure class. [28]
Observing that, in the above estimation, no role exists for the price of intermediate imports relative to that for non-traded goods, we also allow for separability in consumption. We consider that producers may allocate their expenditure on intermediate imports according to the price of such goods relative to the price of domestic substitutes. Even in this case, no role for relative prices is found. Whilst this is not to say that there is no role for relative prices, there is no statistical indication that it influences the demand for intermediate imports. See Bullock et al. (1993) for a discussion about why such price elasticities may be low. [29]
Magee (1975) discusses the ways in which a price elasticity for aggregate imports can be subject to error when the elasticities of the component classes of imports vary through time. Menon (1993) examines this issue further and shows that the aggregate price elasticity is a function of the disaggregated price elasticity for each class of import (i), i's share of total imports and the variation in the price of i relative to the price of total imports. [30]
See Horton and Wilkinson (1989) for a similar approach. It should be noted, however, that this approach abstracts from the effect that reductions in protection have had on GNE and relative prices over the period. [31]
As the model is non-linear in levels, percentage point contributions of each explanator do not sum to the estimated long-run growth. [32]
Alternatively, one might ask what would have happened if tariffs had changed, all other things being constant? This approach has less intuitive appeal given that the other variables by their very nature change, whereas tariffs are set by policy. However, when this alternative approach is adopted, it produces estimates of the contribution of falling protection to import volumes that are only marginally lower than those presented in Table 3. [33]