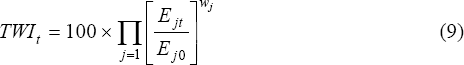RDP 9304: Exchange Rate Pass-Through: The Different Responses of Importers and Exporters Appendix 1: Data
May 1993
- Download the Paper 115KB
All data series are quarterly from 1974:3 to 1992:4, seasonally adjusted (unless otherwise mentioned) and based in 1989/90 prices and period average where relevant.
(a) Domestic Prices – IPDm and IPDx
Implicit price deflators are used for the prices of endogenous imports and manufactured exports, both of which have computers excluded. Manufactured exports are defined as the three ABS categories: Machinery; Transport Equipment; and ‘Other Manufactures’. Computer data are unpublished and non-seasonally adjusted ABS data (seasonal adjustment does not appear warranted). For computer imports, Standard Industrial Trade Classification categories 752 and 75997 are used. For computer exports, only the more general SITC division 75 was available and only from 1978:3.[35]
Source: ABS, Catalogue No. 5302.0
(b) Indices of World Traded Goods Prices – WPm and WPx
The WPm is measured by creating an index of export prices of Australia's major non-oil trading partners. The weights are based on merchandise imports shares into Australia over the period 1980/81 to 1985/86. The index is calculated as:
where: ˙ denotes percentage change; wi is the average share of goods imported into Australia
from 1980/81 to 1985/86 from country i over all countries in the sample;
and
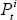 is an index of export prices for country
i. WPx is calculated as in (8) but weights are replaced
by the average share of goods exported to the world from 1980/81 to 1985/86
from country i over all countries in the sample.
is an index of export prices for country
i. WPx is calculated as in (8) but weights are replaced
by the average share of goods exported to the world from 1980/81 to 1985/86
from country i over all countries in the sample.
The index is calculated as a weighted sum of the percentage changes in the foreign indices of export unit values. Percentage changes are used in order to minimise the error resulting from utilising weights based on the proportion of expenditure on imports, rather than the physical quantity of imports. The index is constructed using fixed weights because, for a similar reason, using variable weights would magnify the error in the index.[36]
The countries included in the world price indices and their weights are:[37]
| Weights (wi) | ||
|---|---|---|
| WPm | WPx | |
| USA | 0.268 | 0.195 |
| Japan | 0.259 | 0.148 |
| UK | 0.088 | 0.089 |
| Germany (western) | 0.076 | 0.167 |
| New Zealand | 0.044 | 0.005 |
| Taiwan | 0.038 | 0.025 |
| Italy | 0.033 | 0.071 |
| Singapore | 0.031 | 0.020 |
| Canada | 0.027 | 0.074 |
| Hong Kong | 0.026 | 0.024 |
| France | 0.026 | 0.093 |
| Sweden | 0.019 | 0.027 |
| South Korea | 0.017 | 0.024 |
| Netherlands | 0.016 | – |
| Switzerland | 0.013 | 0.025 |
| Malaysia | 0.012 | 0.013 |
| Belgium | 0.008 | – |
The export price data are unit value data, with the method of construction varying across countries.[38] Lipsey, Molinari and Kravis (1991) and Alterman (1991) discuss the limitations of using unit value data in international studies. The most prominent drawback is that the unit value data generally do not account for quality changes. For most countries, however, the index of export unit values is the only price series available relating to external trade.
These countries accounted for 81 per cent of total merchandise imports in 1991/92. Three countries which might have been included on the basis of trade importance, Saudi Arabia, Kuwait and Indonesia, were excluded because the majority of imports from these countries were petroleum related.
Source: IMF, International Financial Statistics; IMF, Direction of Trade Statistics; Hong Kong, Monthly Digest of Statistics; Taiwan, Financial Statistics; Council for Economic Planning and Development, Taiwan, Industry of Free Choice; and ABS, Catalogue No. 5437.0.
(c) Effective Exchange Rate Indices – TWIm and TWIx
The trade weighted indices are calculated as geometrically weighted averages of the bilateral exchange rates of the 17 countries included in the index of world traded goods prices. The index is calculated according to the formula:
where: Π is the product operator; Ejt is the number of Australian dollars per unit of foreign currency at time t; Ejo is the number of Australian dollars per unit of foreign currency for country j in the base period; and wj is the weight of country j.
For TWIm the weights are based on the merchandise import shares of each country. Similarly, for TWIx weights are based on each country's share of Australia's manufactured exports. The weights are calculated from annual trade data.
Source: Reserve Bank of Australia; ABS, Catalogue Nos. 5437.0 and 5410.0.
(d) Other series used
Published TWI. Source: Reserve Bank of Australia, Bulletin.
Annual Inflation Rate is based on the CPI All groups, weighted average of eight capital cities (non-seasonally adjusted). Source: ABS, Catalogue No. 6401.0.
The retail import price is the CPI for wholly or predominantly imported goods, non-seasonally adjusted, available from 1984:3. Source: ABS, Catalogue No. 6412.0.
The GDP gap is the ratio of real GDP to potential real GDP. Potential GDP is derived from the application of the Hodrick Prescott (1981) filter. Source: ABS, Catalogue No. 5206.0.
The domestic price of manufactures is the Price Index of Manufactured Articles Produced (non-seasonally adjusted, base year 1988/89). Source: ABS, Catalogue No. 6412.0.
Invoicing currency. Source: ABS, unpublished.
Import Price Index of Consumption goods. Source: ABS, Catalogue No. 6414.0.
(e) Time Series Properties of the Data
Each of the series used in estimating the cointegrating relationship was tested for non-stationarity using the Augmented Dickey-Fuller test (Said and Fuller 1984), and the Zt test (Phillips and Perron 1988). The null hypothesis for both tests is non-stationarity.
Four lags on the differenced series were included initially in the ADF test. Lagrange multiplier tests were conducted to test for first, and joint first to fourth order autocorrelation. The test statistic was taken from the specification of the ADF test which was free from autocorrelation and had the smallest lag structure.
A time trend was initially included in the ADF tests on the log levels of the series. In each case the time trend was insignificant.[39] The results reported in table A2.1 are for the tests including a constant only. For the Zt test 5 lags of the covariance were included.
| ADF | Zt | ||
|---|---|---|---|
| IPDm | level 1st difference |
−0.50 −4.18 |
−0.67 −7.31 |
| IPDx | level 1st difference |
−0.55 −4.49 |
−0.69 −8.07 |
| WPm | level 1st difference |
−2.25 −4.22 |
−1.96 −4.45 |
| WPx | level 1st difference |
−2.17 −3.97 |
−2.08 −4.15 |
| TWIm | level 1st difference |
−1.21 −3.83 |
−1.70 −8.18 |
| TWIx | level 1st difference |
−1.14 −4.65 |
−1.28 −6.92 |
Table A2.1 presents the results of the testing on the log-level and log-difference for each series. All series were found to possess one unit root.
The critical values are taken from Fuller (1976):
- −3.51 at the 1 per cent level;
- −2.89 at the 5 per cent level; and
- −2.58 at the 10 per cent level.
Quite clearly, for every series the null hypothesis of non-stationarity is accepted at the 10 per cent level for log levels, and rejected at the 1 per cent level for first differences.
Footnotes
SITC division 75 is for Office Machines and Automatic Data Processing Equipment. SITC categories 752 and 75997 are for computer equipment and computer parts respectively. [35]
Applying the weights to the levels of the foreign index of export unit values results in an Laspeyres index of world prices in the current period multiplied by world prices in the base period. [36]
The weights vary slightly over the sample period as price data are not available for all countries over the whole period. [37]
Constructed variously as Laspeyre, Paasche, and Fisher Ideal indices. [38]
The significance of the time-trend was tested using the critical values from Dickey and Fuller (1981). [39]