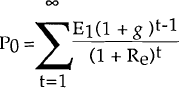RDP 9205: Measuring the Cost of Capital in Australia 2. What is the Cost of Capital?

Modern financial theory – and increasingly corporate practice – says that firms should evaluate investment projects based on discounted cash flows. The ‘Net Present Value’ method involves discounting cash flows (operating returns and scrap value, less initial purchase price and taxes net of concessions) at an appropriate rate and proceeding with those projects with a positive NPV (or if capital constrained those with high NPV/outlay). The ‘Internal Rate of Return’ method involves calculating the discount rate at which NPV is zero and comparing this with a ‘hurdle’ rate.

A starting point for setting the appropriate discount rate or hurdle rate is a measure of the cost of acquiring the finance for the project. The cost of funds to the company is the weighted average of the interest rate and the return to equity^[1], less any tax benefits received by the company. In most corporate finance literature, this rate is referred to as the “cost of capital”, but to distinguish it from the more complex concepts examined below, this concept is referred to in this paper as the cost of funds to the company.^[2] The cost of funds is therefore independent of the nature of the project. However, if the project is of above-average risk, then this too must be taken into account in investment decisions.^[3]

The cost of funds would not be a satisfactory basis for comparing different tax regimes (a higher tax rate, other things equal, lowers the cost of funds; this counter-intuitive result arises because the cost of funds incorporates the interest deductibility aspect of taxation, but not the taxation on corporate profit itself. So the cost of funds would be lower in a country with higher company tax). Nor would it be useful for comparing the viability of a particular project under two different depreciation regimes or under different rates of inflation.

The cost of capital is defined in this paper as the gross real return a project needs to earn to be viable. It provides the basis for comparisons across countries and over time, as well as between different tax and depreciation regimes. It can answer such questions as: “what return should public sector projects achieve to put them on an equal footing with private sector projects?” A higher measured cost of capital says that the project must have a higher return to be viable. This may be because of high risks or taxation factors. It may reflect the “mix” of funding between debt and equity. As the calculation is based on historical data rather than (unmeasurable) expectations, it may reflect abnormal actual returns during the data period. This concept of the cost of capital is much richer than the intuitive starting point of some weighted combination of borrowing and equity costs.

Sections 2.1 to 2.3 examine methods for measuring and weighting the two sources of finance which comprise the cost of funds and give examples to show the significance of differing approaches. The distinction between the cost of funds and the cost of capital is the focus of Section 2.5 discusses the implications of dividend imputation.

2.1 The Cost of Equity

Measurement of the cost of equity is probably the most difficult and controversial aspect of this procedure. Three common methods of estimating the cost of equity are: the capital asset pricing model; the earnings/price model; and the realized gains approach.^[4]

2.1(a) Capital Asset Pricing Model (CAPM)

The CAPM, developed by Sharpe (1964) and Lintner (1965), is a widely used approach to estimate the cost of equity for individual companies. It focuses on why required rates of return may vary across stocks. It is assumed that firms need not compensate individuals for firm-specific risk because it is easy for an individual to hold a well-diversified portfolio of investments.^[5] The relevant measure of risk is thus “beta”, a measure of the covariance between returns for the individual security and returns on the market portfolio. A beta of more than one means that the security's return tends to move more than proportionally with movements in the market; in this sense it is riskier than the market portfolio and shareholders demand a higher-than-market return.^[6]

When estimating the cost of equity for the economy as a whole, beta equals one and the CAPM becomes similar to the realized gains approach (discussed below). However, the CAPM has also been extended to an international context, where betas are estimated for each country relative to the world market.^[7]

2.1(b) Earnings/Price Model

Another approach for estimating the cost of equity is the earnings/price model. In this model, the cost of equity is assumed to be the discount factor implicitly adopted by shareholders when determining the present value of their expected returns, that is the share price. This discount rate takes into account the opportunity cost and the riskiness of the project. Assuming the stream of income to the shareholder is represented by company earnings^[8], the relationship between future earnings (Et), the cost of equity (Re), and the current market price of the stock (P₀) is^[9]:

The E/P model can be rewritten to allow for constant expected growth of earnings (g):

This expression can be rearranged to give the required return to equity as a function of the E/P ratio and the expected growth rate of earnings.

The first term on the right hand side of equations (3) is intuitive – if potential investors demand immediate high rates of return then the cost of attracting these investors is high. The E/P model also takes account of investors' assessments of future operating and investment performance. Investors are willing to pay now for expected superior future returns. If investors demand that returns grow rapidly over time then the required return to equity is also high. This is captured by the second term.

The pros and cons of the E/P method are well documented.^[10] In summary:

• data on E/P ratios are easily available; and
• E/P ratios contain useful information regarding the stock market's valuation of future earnings flows, including the riskiness of those flows.

But:

• the ratios are volatile and have a cyclical pattern;
• while the price data are available instantaneously the earnings data have considerable lags; and
• adjustments for expected growth are important to the outcome, but difficult to make and generally unreliable.^[11]

Furthermore, there are limitations inherent in the use of accounting data. During times of high inflation, historical-cost estimates may result in vastly different estimates of earnings and asset values. For example, when fixed assets and inventories are measured at historical cost, during inflationary periods it is quite likely that deductions made from gross income for depreciation will be insufficient to capture the increasing replacement cost of the asset while the income from inventory sales will overstate true income (if the First-In-First-Out method of inventory accounting is used).^[12] The combined effect is to overstate true firm income and to understate the true value of the firm's assets. Alternatively, if an accelerated depreciation schedule is used for taxation purposes, earnings may require an upward adjustment. Thus a rate of return based on historical-cost accounting will be a misleading indicator of a firm's economic performance and of its cost of capital.

Even if efforts are made to adjust accounting earnings to remove biases and the effects of inflation and taxation, problems remain – especially when making cross-country comparisons. Different countries (and indeed, different companies) have different accounting conventions or managerial incentives that may affect reported earnings considerably. It is important to be aware of these differences and, where possible, to adjust properly for them before making international or even inter-company comparisons.

2.1(c) Realised Gains Approach

This approach measures the return to shareholders (usually including capital gains) as a proportion of market value. In this sense, it is similar to the E/P approach and is often used in preference because of its simplicity. While the E/P approach attempts to be forward looking by incorporating the expected growth rate of earnings (and so measures the required, expected or ex-ante rate of return), the realised gains approach relies on the assumption that past returns are an accurate reflection of the returns required by shareholders in the future (and so measures the realised or ex-post rate of return).

Over long periods of time this assumption is reasonable, as investors and lenders probably expect to realise their returns over the long rather than the short term and expect a variety of random shocks (all of which have small probabilities of occurring) during the term of the investment. However, over the short term, this method (and the E/P approach) can be misleading because of the volatility of share prices. It can also give quite contrary signals as to the true cost of equity in periods when alternative rates of return are changing. For example, when interest rates are falling, a comparable decline in the required rate of return on equity is expected. For this to occur stock prices must rise. Using the realised gains method, however, an increase in stock prices appears as a short-term increase in the cost of equity (via an increase in the capital gain).

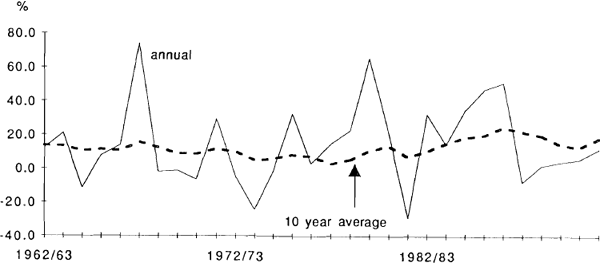
Even over the longer term, the realised gains approach (like the E/P approach) gives estimates which are very sensitive to the time period chosen. The graph below shows two measures, differing in the averaging period, of the (ex post) pre-tax rate of return to shareholders.^[13] The nominal return is calculated from ‘accumulation’ indices which assume all dividends are re-invested. It is clear that the result is heavily dependant on the time period chosen: the annual returns are far more volatile than the ten-year returns. The results for the cost of equity will vary greatly depending on which time period is assumed to be relevant in the formation of expectations.

The following graph compares the realised returns (using the ten-year average) with a measure calculated on the E/P basis. The latter requires an assumption on the expected growth of earnings. Given that the profits share of GDP, while fluctuating over the cycle, has shown no very strong trend, it is assumed that the longer term expected growth in corporate earnings can be proxied by the expected growth in GDP. For the purposes of the graph it is further assumed that the expected longer-term growth rate of GDP is that rate achieved over the previous ten years.

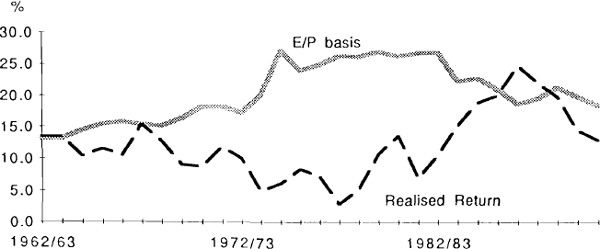
It is clear from the graph that the two approaches yield starkly different results. Even after the decennial averaging, the poor performance of the stockmarket over much of the 1970s and the boom in the mid-1980s causes the realised gains measure to fluctuate much more than has the measure based on E/P ratios. Some would suggest that the 1970s and/or 1980s experiences were exceptional and aberrant and so would not have affected expectations to the extent shown.^[14] It is true that their influence could be almost smoothed away by taking a 20 or 30 or 40 year average. But others would object to an approach which postulated that the cost of equity was virtually constant and barely affected by actual returns. Clearly there is considerable scope for judgement in selecting the appropriate measure. This in itself should give pause to those wishing to present a definitive measure.

2.2 The Cost of Debt

The cost of debt is easier to measure than the cost of equity, since nominal rates of interest are directly observable. Computing a measure is a matter of choosing an interest rate and then adjusting that rate for the tax deductibility of interest payments.

There is no consensus regarding the interest rate(s) that should be used to measure the cost of the debt component of the cost of funds. At an industry level, the cost of debt will vary according to the risk associated with the project. When measuring an average or aggregate cost of debt there appear to be two common methods:

• a medium or long-term industrial funding rate, which represents the average cost of funds over the life of a ‘typical’ private-sector investment project; and
• a weighted-average rate of interest with weights reflecting the mix of debt outstanding in the non-financial corporate sector.

The former approach has been used in a number of Australian studies, including those of Carmichael and Stebbing (1981), Johnston et. al. (1984) and Dews (1989). All these studies used a medium-term industrial debenture rate to represent the cost of debt. The latter approach has been used by Irvine (1991) and the Australian Manufacturing Council (1990) who both used a weighted-average of short-term and long-term rates.

As with the various cost of equity measures, the alternative measures for the cost of debt both have shortcomings. The decision to use a medium or long-term rate is based on the premise that an investment decision is normally long term and that the relevant cost of debt is the expected cost of debt over the term of the project. The cost of debt should represent the opportunity cost of tying the funds up in the project, that is the rate of return that funds invested in a venture of similar risk could have earned.

Presumably a long-term rate will reflect borrowers' expectations regarding interest rates over the life of the project better than will a short-term rate. Borrowers may actually finance long-term investments by ‘rolling-over’ short-term funds (or indeed by utilising an overdraft), but if the expectations hypothesis (which suggests that the term structure of interest rates is determined by investors' expectations regarding future spot rates relative to current spot rates) holds, then the long term rate is still the best measure of the expected cost over the period of the investment. However, Fama (1984) found that the expectations hypothesis does not fully explain the term structure of interest rates.

If the hypothesis is generally false, it may be more sensible to use a weighted-average of short and long-term rates in calculating the cost of debt in cost of capital estimates. However, if the hypothesis is approximately holds, then a weighted average that includes only short-term rates at any one point in time does not adequately reflect information regarding expected future short-term rates. For example, in periods of relatively tight monetary policy (or an inverse yield curve) a weighted-average measure will overstate the cost of capital by not sufficiently allowing for the expected future fall in spot short-term rates.

Almost all measures of the cost of debt include only easily observable, direct interest costs. But bank loans or bond issues may often include fees or may be just one item in a package of services provided by a bank. Furthermore, banks may require corporate borrowers to hold liquid balances yielding less than market rates with them which raises the effective cost of loans.

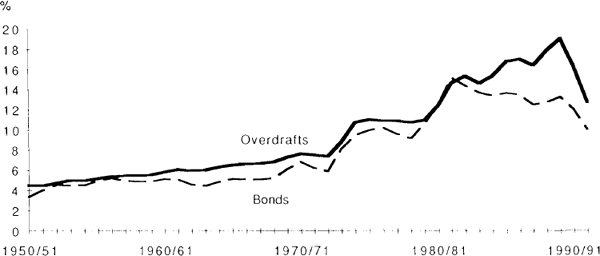
The graph below compares two nominal interest rates for which a run of data is readily available; the prime overdraft rate (a floating rate) and the government 10-year bond rate (a fixed rate). Both will understate the costs of borrowing for many companies, especially in the latter period. Only a very small proportion of bank customers are able to borrow at the prime rate. Banks apply margins over the quoted or ‘prime’ rates to reflect the risk of individual companies. Corporate bonds will have higher yields than government securities, reflecting both the default risk and the partially (though decreasingly so) ‘captive’ nature of the market for government securities. The rate on industrial debentures given in Dews (1988), for example, averaged 2 percentage points above the bond rate over the period 1962 to 1986.

As interest on debt is tax-deductible for companies, the cost of debt should be expressed in after-tax terms. Some studies employ an “effective” tax rate rather than the statutory tax rate. An effective tax rate is the ratio of actual tax paid to earnings after interest (but before any tax allowances). An effective rate less than the statutory rate tells us that the firm is able to reduce its taxable income by an allowance for depreciation or by some other tax allowance. Of course, if changes to the corporate tax system are expected, then these should be incorporated into estimates of the effective tax rate but measuring this effect would be quite difficult. Furthermore, for many purposes it is marginal rather than average tax rates that are relevant. While in the Australian system the average and marginal statutory rates are the same, this is not necessarily true of the effective rates.

2.3 The Cost of Funds

The cost of funds takes into account the after-tax cost of both debt and equity funds.

where:

R_e = average cost of equity;

t_c = corporate tax rate;

R_d = nominal interest rate;

D = value of debt outstanding;

E = value of equity outstanding; and

F = D+E, total funds employed.

Weighting debt and equity to reach a cost of funds creates its own set of conceptual and measurement problems. The available survey evidence shows a variety of responses of firms to these questions.^[15]

In calculating proportions of debt and equity to total funds employed, market value rather than book value weights should be used, in order to be consistent with the market values used in calculating the costs of the various types of financing, and with the aim of maximizing value to shareholders. For pragmatic reasons the market value of equity and the book value of debt are often used.^[16]

As discussed further by Ryan (1990), the mix of debt and equity has changed substantially over time. This should be accounted for in any estimate of the cost of capital. The extent of its impact will reflect both the size of the change in gearing and the difference between the measures of the cost of equity and cost of debt employed.

A problem with using the observed capital structure to weight debt and equity costs arises if corporations are making their investment decisions based on a planned change in the mix of debt and equity. If the target capital structure differs from the current structure, new financing patterns must be used to make the transition. It is the marginal flows of debt and equity in the current period which are relevant to the cost of capital in that period – not the stock of debt and equity outstanding. The latter represents an accumulation of past decisions only. In Australia, changes associated with the introduction of imputation in 1987/88 may have changed the desired mix of debt and equity towards equity. This means that cost of funds estimates using debt to equity ratios based on stock (rather than flow) data and using a similar methodology to that of Carmichael and Stebbing (1981) and Dews (1989) may give undue weight to the cost of debt in recent years.

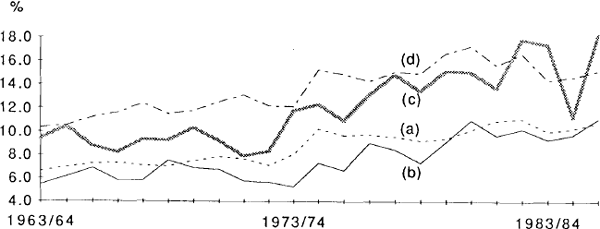
The following graph shows the quantitative importance of some of these factors. The four lines all use the same measures of the costs of debt and equity. They differ only in the weights employed. Measure (a) is based on values for the stock of debt and equity taken from the data on the liabilities of the private non-finance sector. Measure (b) is based on the net changes in these figures each year. (It could be argued that it is the gross changes that are more relevant but data are not available.) Measure (c) is also based on marginal shares but the data are taken instead from financial flow accounts. Measure (d) is based on the market value of debt and equity for a sample of 50–60 companies listed on the Sydney Stock Exchange. It is evident that while the broad sweep of the series are similar, quite different stories could be told about the cost of funds over shorter periods of time depending on the weighting procedure adopted.

2.4 The Cost of Capital

The cost of funds measures the weighted average after-tax cost to the firm of required payments to its debt and equity holders. To derive the cost of capital, the cost of funds must be adjusted for inflation, the taxation of corporate earnings and the tax treatment of depreciation and any other allowances – factors which are likely to differ substantially across countries and projects, even when they are financed identically.

Expected inflation can be measured in numerous ways. One of the most common methods is to use some form of adaptive expectations model, which assumes that expectations are formed on the basis of past inflation. Carmichael and Stebbing (1981) and Dews (1989) followed this approach. In other studies such as the Department of Finance (1987), Australian Manufacturing Council (1990) and Irvine (1991), the inflation rate in the current period is used. These studies implicitly assume that expectations change very quickly and that the present inflation rate contains most of the information relevant to the future values of the inflation rate. Unless this assumption is true, in periods of high inflation these methods overestimate expected inflation and underestimate the real cost of debt and equity.

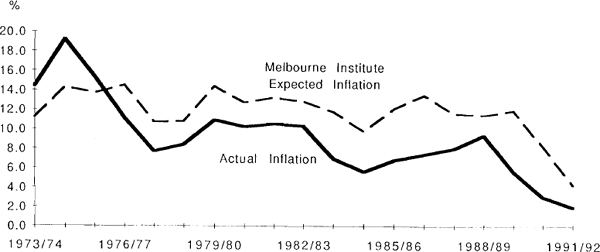
Alternative measures of inflationary expectations can be derived from survey-based measures of expectations, such as the (Melbourne) Institute of Applied Economic and Social Research survey of consumer sentiment (shown in the following graph) and the CAI-Westpac survey of manufacturers. Measures derived from long-term bond yields could also be used. A number of measures of expected inflation are reviewed in Hawkins (1980), Heenan (1991) and Visco (1984). Despite the plethora of available techniques there seems to be no consensus as to which method is best.

The expression for the cost of capital for a generic project with no special tax concessions is therefore;

where p = (expected) inflation.

Substituting from (4) and rearranging allows the expression to be cast in real terms:

2.5 The Effect of Dividend Imputation on the Cost of Capital

The introduction of dividend imputation in 1987 has reduced the differential impact of tax on debt and equity returns. Ryan (1990) concludes that imputation has eliminated the basic source of tax bias towards debt financing, though it has not eliminated all the distortionary effects of inflation on corporate behaviour.

Views differ on the impact of imputation on the cost of capital. Some argue that as Australia is a small open economy with respect to investment funds, the cost of capital will be set in world markets.^[17] A change to a more attractive tax regime for dividend payments will cause the price of shares to rise so as to leave the return to shareholders, after they have paid their personal tax, much the same as before. Another view is that the initial reduction in the cost of capital from imputation will make a number of marginal investment projects viable. Additional projects will be undertaken driving up the marginal cost of equity again.

Officer (1991) argues that a proper measure of the cost of capital needs to take account of the fact that under an imputation system, part of the return on equity represents credits against personal tax. He takes into account the imputation system by replacing the company tax rate in (6) with t(1-g), where g is the proportionate value of personal tax credits. So the cost of capital is :

In the absence of imputation, g = 0, and equation (7) reverts back to equation (6). In a world of full imputation, where the personal tax credits are attributed their full face value by the market (so g = 1) and shareholders face the same marginal rate as companies (7) simplifies to a simple weighted average with no taxation effects.

There are some reasons why it is unlikely that imputation credits will be attributed their full face value by the market. These include:

• all shareholders may not be in a position to make full use of imputation tax credits, as a result of insufficient income and/or concessional tax rates for particular groups such as life insurance companies and superannuation funds;
• the benefits of imputation tax credits are received with a considerable time lag from the time that dividends are actually paid; and
• shareholders may expect further changes in the tax system, suggesting that they may attribute greater risk to the return provided by imputation credits than they do to the return provided by other forms of income.

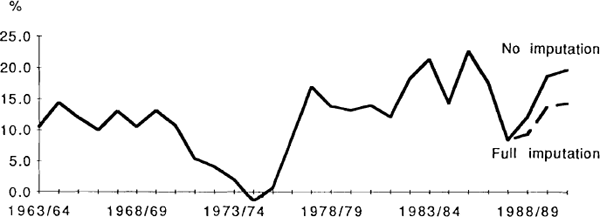
These factors imply that g will be less than 1 but greater than zero. While this answer is unsatisfactory, to be any more precise requires empirical estimation of g. As an indication of the quantitative significance of imputation, the following graph shows two versions of one measure of the cost of capital after the introduction of imputation.^[18] The solid line is based on (6) assuming g = o while the dashed line is based on (8) assuming g = 1.

Footnotes

To avoid unwarranted complexity, it is implicitly assumed in much of this paper that, when looking at the cost of equity, the cost of retained earnings and the cost of issuing new shares are equal. Strictly speaking, differential tax rates on retained and distributed earnings and transactions costs, mean the cost of funds should be a weighted average of the cost of debt, the cost of profit retention, and the cost of new share issues. [1]

From the firm's viewpoint it is not all that important whether the calculations are done in real or nominal terms so long as consistency is maintained. Pohlman et al's (1988) survey of large U.S. firms showed about half the firms used nominal and half real cash flows. Pike (1988) shows a similar variety for the U.K. In this paper we assume the cost of funds is a nominal measure unless otherwise stated. [2]

While adjusting the cost of funds (for example, by applying the Capital Asset Pricing Model -see below) is probably the best way of allowing for risk, in practice other procedures may be followed. Lilleyman's (1984) survey of Australian firms found that 27 per cent incorporated risk by increasing the discount rate while 23 per cent subjectively adjusted the cash flows (other firms did not use discounted cash flow techniques but often changed the payback period to adjust for risk). Gitman and Mercurio's (1982) U.S. survey showed that 32 per cent of firms incorporated risk by adjusting the cost of funds, 39 per cent by adjusting cash flows, 20 per cent by adjusting both and 9 per cent in other ways. Oblak and Helm's (1980) survey of multinational firms showed a similar variety of practice. [3]

The limited survey evidence shows a variety of approaches. In Gitman and Mercurio's (1982) U.S. study 23 per cent of respondents used ‘market return adjusted for risk’ (ie. CAPM or similar), 31 per cent used the ‘dividend yield adjusted for growth’, 16 per cent the earnings/price model and others an unspecified ‘return required by investors’. [4]

See modern financial textbooks such as Copeland and Weston (1983) pp190–192 for a discussion of firm specific (diversifiable) and market (non-diversifiable) risk in the context of the CAPM. [5]

A survey of empirical evidence on the CAPM is given in Section IV of Fama (1991). His basic conclusion is that early tests supported the CAPM but more recent work suggests additional variables to beta, such as size or earnings yield, are also important determinants of returns. The CAPM has also been extended to allow for the effects of taxes arising from dividend payments, uncertain inflation, liquidity, and market capitalisation are discussed in Van Horne (1989), pp. 73–80. [6]

Richards (1991) discusses the International Asset Pricing Model in more detail. [7]

This assumption does not hold if capital gains are taxed differently to other income or if, by accepting retained earnings, the shareholder is able to defer tax payments to a time when they will face a lower tax rate (eg retirement). Note that the E/P model is a variation of the Dividend Discount Model, where it is assumed that dividends paid represent the stream of income to the shareholder. [8]

Throughout this paper, nominal magnitudes are given in upper case, real magnitudes in lower case and growth rates in italics. [9]

See Irvine (1991), Richards (1991), and McCauley and Zimmer (1989). [10]

McCauley and Zimmer (1989), in a widely quoted application of the E/P ratio method, find adjustment for expected growth appears to increase the cost of equity by about 2 percentage points in most countries in most years. Since adjustment for growth does not affect country rankings, McCauley and Zimmer propose that growth potential should be ignored. However, the fact that expected growth does not affect rankings in this case is most likely a by-product of the data used – which were heavily qualified IMF projections of potential business sector output growth for the period 1974 to 1995 and were quite similar for all countries for the period 1989–95. See Adams, Fenton and Larsen (1987) for more details. [11]

See Willmann (1990), p10. [12]

Data and sources are given in Appendix 2. [13]

The Department of Finance (1987) suggest that the cost of capital since the mid-1970s may overstate the long-run required rate because of depressed corporate profitability and instability in crude-oil prices. It is not clear, however, whether the cost of capital in either period, or an average of the two is a better estimate of the long-run expected cost of capital. In order to determine this it would be necessary to know whether the type and frequency of “shocks” to which the Australian economy was exposed during the latter period were abnormal, or whether the relative “calm” of the earlier period was an historical aberration. [14]

Freeman and Hobbes (1991) found that in Australia while 62 per cent of firms constructed a weighted average 28 per cent just used the cost of debt while 2 per cent just used the cost of equity. Oblak and Helm's (1980) survey of multinational firms found 54 per cent using a weighted average, 13 per cent just the cost of debt and 25 per cent just the cost of equity. In Gitman & Mercurio's (1982) U.S. survey 16 per cent of respondents used book values, 29 per cent used market values, 42 per cent used their target weights and 17 per cent used only debt or equity costs depending on how they planned to fund the particular project. [15]

For examples, McCauley and Zimmer (1989), Dews (1989) and Carmichael and Stebbing (1981) use this combination. [16]

Officer (1987) argues along these lines. In this view, any difference in the cost of capital in Australia compared with other countries is explained by distortions in capital markets such as limitations or restrictions on capital mobility or information or differences in investors' aversion to risk in different countries. These factors are likely to be diminishing over time. Tease (1990) finds that there is evidence of increased capital mobility in Australia in the 1980s following financial deregulation. It is generally accepted in Australian studies that rates of return required by investors are set in world markets. Richards (1991) takes the most extreme view evident in recent studies by assuming that Australian equities are priced relative to the world market. They are valued by the way that their returns co-vary with the world market return irrespective of differences in tax treatment of debt and equity. However, Gruen (1991) and Bullock and Rider (1991) argue that high-inflation countries are likely to have relatively high real interest rates. [17]

The magnitude of the imputation effect will depend on the weight given to equity in calculating the cost of funds. [18]