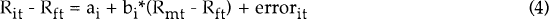RDP 9107: The Cost of Equity Capital in Australia: What can we Learn from International Equity Returns? 3. The Cost of Equity – Theory

(a) Average Realised Returns

According to one view, we need only look at average realised returns on stocks over a long period of time to get a measure of required returns on equity. This view starts with the observation that ex post realised returns are equal to ex ante expected returns plus an unexpected component. But, according to the theory of rational expectations, this unexpected component should have an expectation of zero, so over a sufficiently long time period it should average to zero. Thus, average historical returns will be a good proxy for the required return on equity.

(b) Earnings/Price Ratios

However, ex post returns are not the only way of investigating required rates of return. Indeed, many studies shy away from ex post returns, and instead use approaches based on the market valuation of earnings or dividends.^[8] According to these approaches, it is better to take observed earnings/price (E/P), or dividend/price ratios, since these actually reflect the way that the market has discounted an expected set of future cash flows.

The earnings yield approach is based on the assumption that a company pays out all its earnings in perpetuity, and has the advantage of lifting the corporate veil between earnings retained in the company and those paid out as dividends. Under the assumption that E₁ are the after-tax earnings available either for payout as dividends or for reinvestment, that g_e is the constant rate of growth in earnings that could be maintained (with no reinvestment of earnings) in perpetuity, and that r is the appropriate discount rate, we can derive the following formula for the value of a share:

which implies:

That is, the cost of equity is equal to the prospective earnings yield (E₁/P₀), plus the expected growth of earnings. Note that the earnings growth rate to be used is the rate that would be expected assuming full payout of earnings, so it will be lower than historical earnings growth rates which are boosted by earnings that have been retained in the firm. Note also that the earnings measure used should represent true economic earnings, and not a measure that has been affected by arbitrary accounting decisions.

The issue of whether the formula given by equation 2 is a nominal or a real discount rate is rarely discussed, but some studies have treated E/P ratios differently. For example, both McCauley and Zimmer (1989, p. 27) and the Australian Manufacturing Council (1990, p. 89) assume that E/P ratios correspond to the real cost of equity, while Irvine (1991, p. 15) treats E/P ratios as a measure of the nominal cost of equity.

It is fairly obvious that the answer to this question will depend on whether g_e is a nominal or a real growth rate. Since real earnings growth rates are usually used, it is clear that E/P ratios are a measure of the real cost of equity. That is, a stock can be thought of as an indexed security in many senses.^[9]

However, a slight offsetting factor is that the E/P ratios normally quoted use earnings in the most recent period (E₀), instead of expected earnings (E₁), which will generally be higher than previous earnings, as a result both of inflation and real earnings growth. Assuming growth in the current period due both to real growth in the economy g_y,^[10]and to the inflation rate π, we have:

That is, a small adjustment should ideally be made to E/P ratios that have been calculated using retrospective earnings, but E/P ratios should still be thought of as proxies for the real cost of equity.

(c) The Capital Asset Pricing Model

The two previous measures for the cost of equity say nothing about why required rates of return might vary across stocks or countries. However, another method of estimating the cost of equity is the class of asset pricing theories, starting with the CAPM, and continuing with its extension into the international framework, which attempts to explain why different securities yield different rates of return.^[11] I begin discussion of this literature by reviewing the domestic CAPM.

(i) The Domestic CAPM

According to the standard one-factor CAPM for a domestic market, the risk of a security can be split into two components: risk that is related to the overall market, and risk that is independent of the overall market. Since the latter can be diversified away in a portfolio, but the former remains even in a large portfolio, only market risk is rewarded or priced. It can then be shown that the required return on a security depends on its “beta” (β), which is defined as the expected covariance of that security's return (R_i) with the market return (R_m), divided by the expected variance of the market return. In practice, with R_f as the risk free rate of return, beta is estimated by estimating the following equation:

According to the CAPM, a security with a high beta will have a high required rate of return. A security's beta will depend on two factors, the risk of the cashflows that the underlying asset generates, and the degree of leverage of the firm. Since additional debt makes the returns to equity more risky, the observed beta for any firm is an increasing function of the company's leverage. When estimating the cost of equity for a company, one usually starts with the observed “levered” (or equity) beta (β_l) of the security, and then uses the observed capital structure to “unlever” this beta, to get an “unlevered” (or asset) beta (β_u). If debt is riskless, the formula, known as the Hamada (1969) formula, is as follows:

where t_c is the corporate tax rate, and B/S is the firm's debt/equity ratio, at market values.

The unlevered beta reflects the underlying risk of the asset in question, irrespective of whether it is debt-financed or equity-financed (but after taking account of the tax treatment of the particular financing mix that is used). It can then can be used to “relever” under alternative financing assumptions, to obtain the beta, and the cost of equity that would eventuate under those different assumptions. For the present purposes, the important point is that it is the unlevered beta which is the primary input into the cost of equity (and the cost of capital) for each firm.

(ii) The IAPM

The theoretical literature on the pricing of securities in an international context begins with the work of Solnik (1974) who developed an International Asset Pricing Model (IAPM) similar to the CAPM for securities in a domestic market. Subsequently, Solnik (1983) also extended the Arbitrage Pricing Theory (APT) model into an international context (IAPT). In addition, Stulz (1981) has extended the model along the lines that the consumption-based CAPM extends the simple CAPM.

One problem with models of international asset pricing is that investors in different countries face different opportunity sets since national markets are denominated in different national currencies. If investors of different nationalities had similar consumption tastes and if purchasing power parity (PPP) held for exchange rates, the CAPM could easily be extended internationally. Regrettably PPP has proved to be a poor approximation to reality. However, Solnik (1983) shows that many of these problems would be reduced if exchange rates were determined (in an APT framework) by a similar set of factors to those which determine security returns in each country.

Another problem is that the conditions for arbitrage that the CAPM or APT require are less likely to be observed across countries, because of a range of factors including restrictions on international investment, taxes, and informational problems. However, these factors are presumably becoming much less important as capital controls are removed and as new markets and instruments make international investment easier.

Despite these and other problems, this class of models of international asset pricing all retain the essential insight of the CAPM – that assets will be priced according to the risk that they add, whether it be to the market portfolio, or the level of consumption. Subject to some restrictive assumptions, the IAPM states, “the risk that is priced in the market is measured by the international beta of a security, that is, the beta relative to the world market portfolio hedged against exchange risk” (Solnik, 1988, p. 134). However, the world market portfolio, or any portfolio of risky foreign securities cannot be perfectly hedged against exchange risk, since only principal amounts can be perfectly hedged, leaving the uncertain return component subject to currency risk. As a result, in the analysis of Sections 4 and 5, I make the assumption that by analysing all returns in a common (and in a sense, average) currency like the SDR, I capture most of the insights of the IAPM.

So, to use the IAPM to get estimates of the cost of equity across countries, one must estimate betas for each country relative to the world market, then account for differences in gearing ratios and the tax advantage to debt, and if necessary, then add a factor for the currency risk of investing in each market.

Footnotes

The dividend discount model is similar to the earnings approach, and gives similar conclusions, so I concentrate on the earnings yield approach. [8]

This view is supported by Carmichael (1978, pp. 94–95). [9]

I use g_y as a simplification for the measured growth of earnings, to distinguish it from g_e in equation 2, which is the expected growth of earnings under the full payout assumption. [10]

Much of the analysis can also be thought of in terms of the consumption-based CAPM. [11]