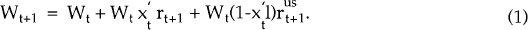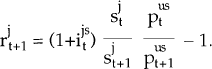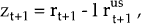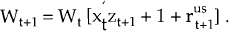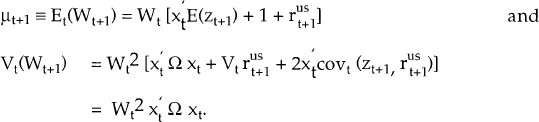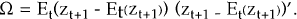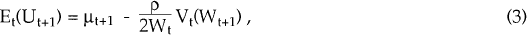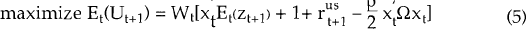RDP 9103: The Failure of Uncovered Interest Parity: Is it Near-Rationality in the Foreign Exchange Market? 2. The Model
May 1991
- Download the Paper 251KB
In this section we derive the optimal allocation of foreign assets in a representative US investor's portfolio. We maximize expected utility in the coming week.
The US investor maximizes a function of the mean and variance of end-of-period real wealth. At the beginning of each week, all the information necessary to accurately forecast end-of-week real wealth is available, with the exception of the exchange rate movements over the week. Prices are not a source of uncertainty by assumption. We allow assets denominated in US Dollars, Yen, Deutschemarks, British pounds, Swiss francs and/or Australian dollars to be chosen for the portfolio.
We contrast different strategies by investors within this model framework. The first ‘rational’ strategy involves the investor maximizing expected utility by choosing portfolio shares of hypothetical weekly securities denominated in the available currencies. Relevant new information arrives weekly, and so this ‘rational’ investor adjusts portfolio shares every week. At the end of each week, the one-week securities mature and new ones are purchased. We assume there are no costs associated with these transactions. Because all the securities are turned over each week, the cost of sub-optimal behaviour arises from holding inappropriate shares of assets, rather than from being ‘locked-in’ at old interest rates (as would be the case if the securities had a term of more than a week).
We now posit an expected utility function and maximize it with respect to the portfolio shares. The analysis follows Frankel and Engel (1984). We use the following notation:
| 1 | – | a vector of ones |
| pus | – | US consumer prices |
| rj | – | the real return in country j |
| sj | – | the exchange rate (value of currency j per $US) |
| U | – | utility |
| W | – | real wealth |
| xj | – | share of portfolio held in foreign country j |
| zj | – | the real return in foreign country j relative to the US |
| ijl | – | nominal long interest rate in country j (expressed per week) |
| ijs | – | nominal short interest rate in country j (expressed per week) |
| ρ | – | the coefficient of relative risk aversion |
| Ω | – | the variance-covariance matrix of real returns relative to the US. |
End-week real wealth is given by
xt is a 5×1 vector of foreign currency shares, 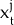 ,
chosen at time t, while rt+1 is a 5×1 vector of real returns available to the
US investor by investing in those countries. The individual elements of rt+1 are
given by:
,
chosen at time t, while rt+1 is a 5×1 vector of real returns available to the
US investor by investing in those countries. The individual elements of rt+1 are
given by:
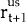 is
similarly defined, without the exchange rate ratio.
is
similarly defined, without the exchange rate ratio.
zt+1 is a 5×1 vector of real returns relative to the US, given by
and hence (1) becomes
The mean and variance of Wt+1 are
The last step follows from the fact that 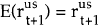 ; by investing in the US
; by investing in the US
the investor removes the only source of uncertainty – exchange rate movements.
The variance-covariance matrix of relative real returns, Ω, is
In order to calculate Et(zt+1) we require a simple and tractable
expression for the expectation of exchange rate changes. Unit-root tests can rarely reject the
hypothesis that nominal exchange rates follow a random walk with no drift (Frankel and Meese,
1987) – which would imply that 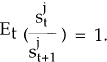
However, these tests are of low power, and they can rarely reject a range of alternative hypotheses.
From the perspective of economic theory it seems plausible that, over time, nominal exchange rates move to offset differences in inflation. We use the difference in long bond rates as a proxy for the expected inflation difference, and assume that,
Equation (2) implies that each real exchange rate is expected to follow a random walk with no drift.[3]
Investors maximize expected utility which is assumed to be a linear combination of the expected value and variance of real wealth. Thus,
where ρ is the coefficient of relative risk aversion evaluated at μt+1.[4]
Maximizing (3) with respect to xt, leads to [5]
This is the key equation which relates the optimal portfolio shares to the mean and variance-covariance matrix of the relative returns.
(a) Introducing constraints on shares
The optimal foreign shares derived from (4) are unconstrained; they can be negative and they can sum to more than one (implying a negative share for the US). A negative share signifies borrowing, say, US dollars to place in a high-yielding low-variance currency.
We now wish to limit the foreign exposure of the portfolio and to impose the constraint that investors don't sell short in a currency – that is, that all shares are non-negative. This is one way to introduce the real-world asymmetry that borrowing and lending rates are not equal.[6] Imposing these additional constraints, the maximization problem is reformulated as follows:
where k≤1 is the maximum foreign exposure of the portfolio.
Any solution of this constrained maximization problem must satisfy the Kuhn-Tucker sufficiency conditions:
- Et(Ut+1) is a differentiable and concave function of xt in the non-negative orthant,
-
the constraint function
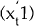 is differentiable and convex in the
non-negative orthant, and
is differentiable and convex in the
non-negative orthant, and
-
the following conditions (omitting the time subscript) hold:
-

- λ≥0; (k−x′1)λ = 0
-
where 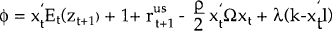
and λ is the Lagrange multiplier for constraint (6).
Condition (a) is satisfied because 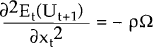 and Ω is positive
definite. Condition (b) is clearly satisfied. Shares from (4) may satisfy constraints (6) and
(7), in which case that is the constrained optimum. Otherwise, we derive a solution by
alternately eliminating from the analysis countries with negative portfolio shares, and, if
constraint (6) is violated, imposing it with equality. The final solution (a 5×1 vector of
non-negative portfolio shares) must satisfy all the Kuhn-Tucker sufficiency conditions for all
countries.
and Ω is positive
definite. Condition (b) is clearly satisfied. Shares from (4) may satisfy constraints (6) and
(7), in which case that is the constrained optimum. Otherwise, we derive a solution by
alternately eliminating from the analysis countries with negative portfolio shares, and, if
constraint (6) is violated, imposing it with equality. The final solution (a 5×1 vector of
non-negative portfolio shares) must satisfy all the Kuhn-Tucker sufficiency conditions for all
countries.
(b) The cost of near-rationality
Assume that at time t, strategy α leads the investor to choose the vector of portfolio
shares 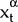 and hence to derive expected utility
and hence to derive expected utility 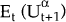 . Further, define
. Further, define 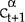 by the
equation
by the
equation
Finally, define cα as the arithmetic average of 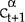 over the sample. For any given strategy α, the average equivalent riskless return forgone (AERRF)
is copt – cα, where copt is the value of
cα when α is the optimal strategy.
over the sample. For any given strategy α, the average equivalent riskless return forgone (AERRF)
is copt – cα, where copt is the value of
cα when α is the optimal strategy.
Evaluating the AERRF allows us to quantify and compare the costs of various sub-optimal strategies. Note that the loss associated with any near-rational strategy consists of having inappropriate portfolio shares – rather than missing out on interest rate changes which may turn out to be favourable.
We wrote a GAUSS program to evaluate the optimal portfolio shares under three regimes. In turn, we assumed that foreign portfolio shares were (i) unconstrained, and hence given by equation (4), or (ii) constrained to be non-negative and with a maximum foreign exposure of 100% (i.e., k = 1 in equation (6)) or, (iii) constrained to be non-negative and with a maximum foreign exposure of 40% (i.e., k = 0.4 in equation (6)). In each case, we evaluated the expected utility cost (AERRF) when the investor optimizes every 1, 2, 3, 4, 13, 26 and 52 weeks. By assumption, optimizing every week is fully optimal and so the associated AERRF is zero. The results were derived using 302 weeks of data on short and long-term interest rates, and an empirical estimate of Ω (see the Data Appendix and the Appendix for details). Figure 1 shows the results assuming ρ = 2, 10 and 20, as Cecchetti and Mark (1990) suggest that there may be a range of possible values for ρ.[7]
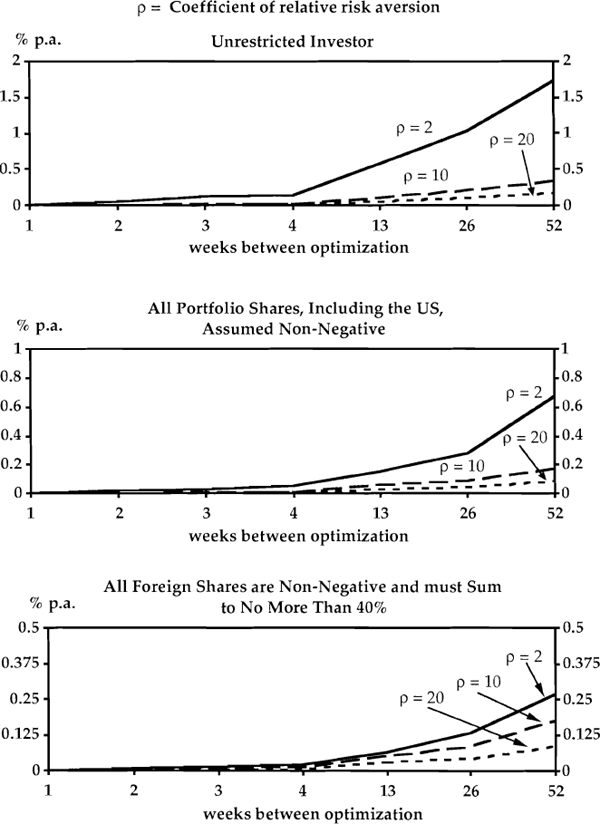
Perhaps the most realistic simulations are those shown in the middle panel of Figure 1, which assume that all portfolio shares (including the US share) are non-negative. Assuming ρ = 2, the expected utility cost of adjusting portfolio shares every four weeks averages about 0.05%p.a. while the cost of adjusting every three months (13 weeks) averages about 0.16% p.a. If ρ> 2, these costs are even smaller (see Figure 1).
Footnotes
Note that equation (2) implies a rejection of uncovered interest parity because the expected exchange rate change is not determined by the short-term interest differential. The point of the paper is to estimate how much is lost by not taking full advantage of the gap between the expected exchange rate change and the short-term interest differential. The Discussion section examines an alternative to the assumption that the real exchange rate follows a random walk. [3]
Equation (3) embodies the approximation that ρ ≡ −μt+1· U″(Wt+1)/U′(Wt+1)≈ −Wt· U″(Wt+1)/U′(Wt+1). This approximation makes the algebra simpler and is empirically harmless since 1< μt+1/Wt<1.01. [4]
Frankel and Engel (1984) have an additional term here which arises from their assumption of stochastic US prices. [5]
By making Et(zt+1) the subject of (4), it becomes apparent that relative returns are a linear function of xt, i.e., that borrowing and lending rates are assumed to be the same. [6]
Our enquiries suggest that many fund managers do not hold more than a proportion k (with
k < 1) of their portfolio overseas – presumably because they are risk-averse.
In our framework this implies that 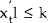 , and manipulation of (4)
gives ρ≥[(kΩ)−1Et(zt+1)]'1. A
money market corporation (which practices ‘active’
portfolio management), an insurance company and a state-government corporation offered
upper bounds on the size of the hypothetical investor's overseas portfolio share of
45%, 40% and 20% respectively, k = 20% (45%) implies ρ≥ 10 (4.4) on average over
the period. We therefore have some additional grounds for experimenting with values
of ρ larger than 2.
[7]
, and manipulation of (4)
gives ρ≥[(kΩ)−1Et(zt+1)]'1. A
money market corporation (which practices ‘active’
portfolio management), an insurance company and a state-government corporation offered
upper bounds on the size of the hypothetical investor's overseas portfolio share of
45%, 40% and 20% respectively, k = 20% (45%) implies ρ≥ 10 (4.4) on average over
the period. We therefore have some additional grounds for experimenting with values
of ρ larger than 2.
[7]