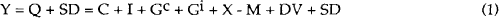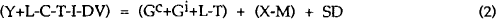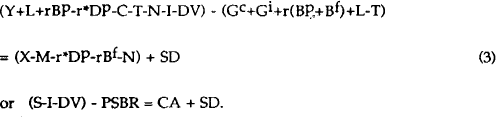RDP 9002: Public Sector Growth and the Current Account in Australia: A Longer Run Perspective 2. An Accounting Framework
July 1990
- Download the Paper 1.2MB
The framework in this section is familiar from other discussions of fiscal policy and the current account.[3] The identities not only provide a framework for understanding the economy, but also allow analysis of the sustainability of a given level of domestic or external debt.
A natural starting point to examine the relationship between saving, fiscal policy and the current account is the National Income identity. We start from the market clearing condition for the supply and demand for goods and services. If economy-wide income is equal to expenditure on goods and services (adjusted by a statistical discrepancy) we get:
where all variables are in current dollars and
| Y | = | national income; |
| Q | = | production of domestic goods and services; |
| SD | = | the statistical discrepancy; |
| C | = | total private consumption of goods and services; |
| I | = | total private purchases of goods and services for investment; |
| Gc | = | total government consumption of goods and services ; |
| Gi | = | total government purchases of goods and services for investment; |
| X | = | exports of domestic goods and services; |
| M | = | imports of goods and services; and |
| DV | = | change in stocks of goods. |
Note that the measure of income in the National Accounts is not strictly the economic concept of income because it ignores several items, especially the role of capital gains as part of income.[4] The implications of this for the 1980s is that income is likely to be underestimated. The corollary is that saving may also be underestimated.
By subtracting and adding total taxes (T) and government transfers to the private sector (L) respectively, equation (1) can be rearranged to get sectoral relationships:
We will refer to the first term as the (net-of-interest) private saving/investment balance, the second term as the primary fiscal balance and the third term as the trade balance. Finally if we assume that Australia is a net debtor, we add net interest flows and other non-interest income and net transfers to foreigners (N) to both sides of equation (2), to derive the relationship between the current account and the public sector borrowing requirement (PSBR)[5]:
Where:
| r | = the domestic interest rate on government debt; |
| r* | = foreign interest rate on external debt; |
| BP | = net government debt held by the domestic private sector; |
| Bf | = net government debt held by foreigners; |
| DP | = net private debt held by foreigners; |
| S | = private saving; |
| PSBR | = public sector borrowing requirement (government dis-saving); and |
| CA | = current account surplus (economy saving). |
In short, the excess of private saving over investment plus government saving is approximately equal to the current account. It is clear from this identity that an increase in government dis-saving (i.e a fiscal deficit) for a given level of private saving and investment will imply an increase in the current account deficit; an economy which invests more than it saves will finance this by borrowing from foreigners.
In addition to this static identity we also need to introduce some intertemporal identities. These link flows and stocks. For example, a current account deficit implies a build-up of foreign debt and a fiscal deficit implies a build-up of government debt, both of which need to be serviced. This affects the size of future current account deficits and fiscal deficits, which affect future behaviour of the private sector. The future servicing of accumulated debt will affect asset markets in the present.
First consider the accumulation equation for the debt of the economy as a whole[6]:
where D is in domestic currency units and et is the rate of depreciation of the nominal exchange rate during period t. This equation shows that the change in debt is equal to the trade balance deficit (M-X) plus the servicing costs of the outstanding stock of foreign debt. Even in the case of balanced trade, an initial debt will lead to an ever-increasing stock of debt. A trade balance surplus (X>M) would be required to service the debt and hence to achieve current account balance.
This relationship may be expressed in terms of the ratio of debt to GDP. In this case it can be shown that:
In equation (5) we now use lower case letters to denote variables as a proportion of GDP, and we have introduced a term n which is the nominal growth rate of the economy. It can be seen from equation (5) that stabilization of the ratio of debt to GDP implies a different trade balance to that required for the level of debt to stabilize. In particular, if the nominal growth rate of the economy is greater than the interest rate on the debt (adjusted for exchange rate changes), the economy can still run a trade balance deficit and stabilize the ratio of debt to GDP. In other words, it is quite possible that the future flows of production generated in the economy will be more than capable of servicing a growing foreign debt.
Recent theory suggests that these intertemporal identities have important implications for short run behaviour because of the links between the future path of the economy and current asset prices.[7] This will be elaborated below.
Footnotes
See for example Genberg (1988). [3]
See Eisner (1989) for a good outline of the many problems with interpreting National Accounts data. [4]
Note that we include public authorities as well as state and local government in our definition of government. The actual PSBR also includes miscellaneous items such as non-tax revenue, provisions for depreciation and asset sales, etc. [5]
Note that, for simplicity, we have ignored the other income transfers which appear in the current account. In this example we have also assumed that all debt is short term, denominated in a single foreign currency and paying the same foreign rate of interest. The current account is also assumed to be funded by debt; equity flows are ignored. [6]
For example see Sachs and Wyplosz (1984). [7]