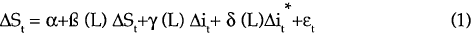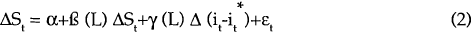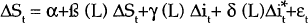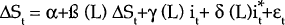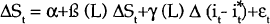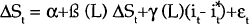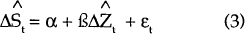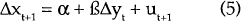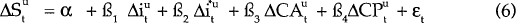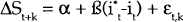RDP 8908: Capital Flows and Exchange Rate Determination Appendix: Tests of the Relationship Between Nominal Interest Rates and the Exchange Rate
December 1989
- Download the Paper 1.12MB
1. Direct Tests of Exchange Rate Sensitivity to Relative Interest Rates
The following equations were estimated to examine the sensitivity of exchange rates to short-term interest rates (equations 1 and 2 in the text).
where,
| S | = | log of the spot exchange rate; |
| i | = | 90-day Australian bank-bill rate; and |
| i* | = | 90-day foreign Euro-rate. |
These equations were estimated on the basis of both weekly and monthly data between 1983 and 1989. The data were obtained from the International Department of the Reserve Bank. All data were sampled on Wednesdays.
Earlier tests revealed that most of the series had at least one unit root, indicating the need for first differencing in estimation.[16] Equations which use levels rather than first differences of the interest rate terms were also estimated to see if the results were sensitive to differencing. This was not the case.
Some summary statistics from estimating equations 1 and 2 are presented in Tables 2 and 4. The equations which use levels rather than first differences of the interest rate terms are presented in Tables 3 and 5. The statistics reported in the Tables are F-tests of the exclusion of the lags of the relevant interest rate variable. A significant value of the statistic indicates that the hypothesis that the coefficients on the lagged interest rates are zero can be rejected. Two sets of results are reported; one for equations estimated for weekly changes and one for monthly changes.
| Exchange Rate |
Δit | Δit* | ||
|---|---|---|---|---|
| Weekly | Monthly | Weekly | Monthly | |
| US$/AUD | 0.81 | 1.27 | 0.83 | 1.00 |
| YEN/AUD | 1.60 | 1.41 | 2.53* | 0.26 |
| DM/AUD | 2.09 | 0.53 | 1.76 | 0.73 |
| £/AUD | 1.04 | 0.51 | 3.64** | 1.41 |
|
*(**) Significantly different from zero at the 5(1) per cent level. |
||||
| Exchange Rate |
it | 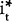 |
||
|---|---|---|---|---|
| Weekly | Monthly | Weekly | Monthly | |
| US$/AUD | 1.09 | 1.35 | 0.86 | 1.03 |
| YEN/AUD | 1.46 | 0.95 | 2.78* | 0.32 |
| DM/AUD | 1.77 | 0.53 | 2.01 | 0.56 |
| £/AUD | 0.68 | 0.58 | 3.64** | 1.52 |
See footnotes Table 2. |
||||
| Exchange Rate |
Δ(it−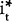 ) )
|
|
|---|---|---|
| Weekly | Monthly | |
| US$/AUD | 1.02 | 1.68 |
| YEN/AUD | 3.09* | 1.52 |
| DM/AUD | 2.30 | 1.35 |
| £/AUD | 3.53** | 2.27 |
See footnotes Table 2. |
||
| Exchange Rate |
(it−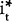 ) )
|
|
|---|---|---|
| Weekly | Monthly | |
| US$/AUD | 0.43 | 1.70 |
| YEN/AUD | 3.52** | 1.47 |
| DM/AUD | 2.59* | 1.63 |
| £/AUD | 3.37** | 2.32 |
See footnotes Table 2. |
||
The results, in general, indicate that the null hypothesis cannot be rejected. Weekly or monthly changes in domestic interest rates are not significantly related to weekly or monthly changes in the exchange rate. In general, this was also true of foreign rates, although there was some evidence of a relationship between weekly movements in Japanese and U.K. rates and the exchange rate. This was not the case in the monthly equations.
2. Unanticipated Exchange Rate Movements in Response to “News”
It is well known that interest differentials (or forward premia) do not forecast short-term movements in the exchange rate with any degree of accuracy. The tests of uncovered interest parity reported later illustrate this point. Furthermore, the forecasting performance of structural and time series exchange rate models is not generally superior to a random walk model. This poor forecasting performance is not surprising since unanticipated movements in the exchange rate account for most of its short-run volatilty (see Mussa (1979)). In an asset market model, these unexpected movements are due to unanticipated changes in its determinants.
This section of the appendix explores the extent to which short-run volatility of the exchange rate can be explained by unanticipated changes in its determinants. To do this we estimate (equation (3) in the text):
where,
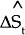 |
= | unanticipated change in the exchange rate; |
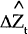 |
= | unanticipated change in a vector of determinants. |
We assume that the relevant determinants are domestic and foreign interest rates, the current account and commodity prices. It would also be desirable to include some measure of inflation and the money supply as determinants. (However, see footnote 9 for the problems in doing so.)
To construct estimates of the unanticipated changes, we estimate the following forecasting equations:
where,
| x | = | variable being forecast; |
| y | = | vector of variables in the information set; and |
| u | = | forecast error. |
This equation is estimated for the exchange rate and each of its determinants.
The estimated forecast errors 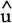 t+1 are then extracted from
the various equations and used as proxies for the unanticipated change in the variables. The
following equation was then estimated:
t+1 are then extracted from
the various equations and used as proxies for the unanticipated change in the variables. The
following equation was then estimated:
where,
| S | = | nominal exchange rate; |
| i | = | domestic 90-day bill rate; |
| i* | = | overseas 90-day Eurorate; |
| CA | = | current account deficit; and |
| CP | = | commodity prices. |
Unanticipated changes are denoted by the superscript u.
OLS estimation of equation (6) will yield consistent estimates of the β's (see Pagan (1984)). The results of estimating equation (6) for four bilateral exchange rates of the Australian dollar and a trade-weighted index are reported in Table 7.
| Exchange Rate | α | 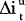 |
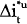 |
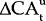 |
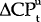 |
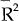 |
DW |
|---|---|---|---|---|---|---|---|
| US$/AUDu | 0.00 (0.00) |
−0.97* (0.49) |
0.18 (1.26) |
−0.00 (0.00) |
0.32 (0.21) |
0.07 |
2.03 |
| DM/AUDu | 0.00 (0.00) |
−0.84 (0.56) |
1.84 (1.90) |
0.01 (0.01) |
0.96** (0.24) |
0.22 |
1.88 |
| YEN/AUDu | 0.00 (0.00) |
−1.24* (0.60) |
−0.59 (1.92) |
0.01 (0.01) |
0.67* (0.27) |
0.13 |
1.95 |
| £/AUDu | 0.00 (0.00) |
−1.06* (0.52) |
0.89 (0.68) |
0.00 (0.01) |
0.50* (0.24) |
0.10 |
2.07 |
| TWIu | 0.00 (0.00) |
−0.87 (0.50) |
0.83 (1.26) |
0.01 (0.01) |
0.76** (0.20) |
0.22 |
1.95 |
Standard errors are in brackets. |
|||||||
The foreign interest rate term reported in the TWI equation in the table is 90-day US Eurorate. Other foreign rates were tried in the equation and they were also insignificant.
Sample: January 1984 – April 1989.
Three points emerge from these results. First, unanticipated changes in the exchange rate are significantly related to unanticipated changes in commodity prices. An unanticipated rise in commodity prices leads to anappreciation of the currency in four of the five Australian dollar exchange rates tested. This suggests that not only do commodity prices explain part of the longer-run movement in the exchange rate, they also account for some of its short-run volatility. It is interesting (and somewhat surprising) to note that the US$/AUD exchange rate is the only one not significantly related to commodity prices. Its importance, however, is not large enough to detract from the significant relationship found for the (more important) trade-weighted index.
Second, there is a negative correlation between unexpected changes in the exchange rate and the domestic interest rate. In three cases, the coefficient is significant at the 5 per cent level. The negative relationship is consistent with the observation in the text that the results are dominated by the policy reaction function that operated for much of the sample period. That is, unanticipated shocks to the exchange rate led the Reserve Bank on a number of occasions to alter domestic interest rates.
Finally, unanticipated movements in the determinants only account for a small part of the volatility of exchange rate.
3. Uncovered Interest Parity
When capital is perfectly mobile, and agents are risk neutral and rational, then capital flows should ensure that expected returns are equal across countries. That is, uncovered interest parity should hold. The uncovered interest parity hypothesis states that nominal interest differentials between similar assets denominated in different currencies equal (in the absence of a risk premium) the expected change in the exchange rate. Thus,
where,
| St | = | logarithm of the spot exchange rate in period t; |
| E( ) | = | expectational operator; |
| ϕt | = | information set in period t; |
| it | = | k-period domestic nominal interest rate in period t; and |
| it* | = | k-period foreign interest rate in period t. |
Equation (7) states that the differential between k-period nominal interest rates equals the expected change in the exchange rate over the next k periods. Assuming that agents expectations are formed rationally[17] allows us to derive an estimable form of equation (7) (this is equation (4) in the text):
If expected returns are equalised across countries then α=0, β=1 and εt,k is a white noise process. One of the stylised facts of the international experience with floating exchange rates is that uncovered interest parity does not hold. Furthermore, to the extent that nominal interest differentials (or forward premia) provide any information on short-run changes in the exchange rate, this is dominated by movements in εt,k.
Estimates of equation (4) for a number of bilateral rates are reported in Table 8. The data are weekly observations on 90-day Australian interest rates and 90-day Eurorates for the foreign currencies. The sample period is January 1984 to May 1989.
| Exchange rate | 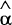 |
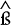 |
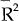 |
|---|---|---|---|
| US$/AUD | −0.26 (−0.26) |
0.359 (0.317) |
0.026 |
| DM/AUD | 0.027 (0.050) |
−0.534 (0.453) |
0.022 |
| £/AUD | −0.024 (0.043) |
0.317 (0.807) |
0.002 |
| YEN/AUD | −0.01 (0.02) |
−0.255 (0.604) |
0.002 |
Hansen-Hodrick standard errors are in brackets. |
|||
Uncovered interest parity is resoundingly rejected in most cases. In the £/AUD equation,
 is within
two standard errors of one. However, the confidence interval is so large that the hypothesis
is within
two standard errors of one. However, the confidence interval is so large that the hypothesis
 =0 also
cannot be rejected. The nominal interest differential is found to have no explanatory power in
predicting future movements in the nominal exchange rate. These results are consistent with
earlier Australian evidence examining the behaviour of the US$/AUD exchange rate reported in
Tease (1988) and Smith and Gruen (1989) and with other international evidence; see Hansen and
Hodrick (1980) and Cumby and Obstfeld (1984) for examples.
=0 also
cannot be rejected. The nominal interest differential is found to have no explanatory power in
predicting future movements in the nominal exchange rate. These results are consistent with
earlier Australian evidence examining the behaviour of the US$/AUD exchange rate reported in
Tease (1988) and Smith and Gruen (1989) and with other international evidence; see Hansen and
Hodrick (1980) and Cumby and Obstfeld (1984) for examples.
Footnotes
Tests were also conducted to see if the exchange rate and the relevant interest rate variables were cointegrated. The tests did not find any evidence of cointegration. Attempts to estimate (1) and (2) as error correction models were therefore not conducted. [16]
That is, agents expectations are, on average, realised so that E(St+k| ϕt) = St+k + εt,k. Where εt,k is a white noise process orthogonal to elements of ϕt. [17]