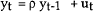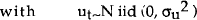RDP 8903: The Relationship Between Financial Indicators and Economic Activity: Some Further Evidence 3. Data

Glenn Stevens and Susan Thorp

June 1989

(a) Indicators of Financial Conditions and Economic Activity

The variables used in BMS were:

  • the yield on 90-day bank-accepted bills;
  • monetary aggregates M1, M3, and broad money;
  • lending/credit aggregates bank lending, lending by all financial intermediaries (AFI lending) and credit; and
  • private final demand (PFD) , both in current and constant prices.

All variables were in seasonally adjusted form, except the bill rate.

The data used in Section 4 of this paper are the same, except that:

  • national accounts aggregates have been re-based to 1984/85 prices for the constant-price series;
  • all series have been updated to the September quarter 1988, two quarters later than in BMS;
  • GDP is used, as well as private final demand, as an indicator of activity; and
  • the analysis is conducted using unadjusted (results reported in Appendix B) as well as seasonally-adjusted data.

Details of data definitions, etc. are in Appendix C. The actual data used are reproduced at the end of the paper.

(b) Differencing and Detrending

Standard econometric tests, including those used in VAR analysis, assume that the time series used in estimation are stationary; that is, that the mean and variance of the distributions from which the observations are drawn are unchanging through time. This assumption is rarely true for levels of macroeconomic time series. Most series must be made stationary, usually by detrending or differencing, before reliable econometric models can be estimated and tests conducted.

Economists frequently detrend data on the assumption that series have a secular (trend) and a cyclical component. However some recent studies (eg Nelson and Plosser (1982)) have suggested that many macroeconomic series may actually have stochastic, rather than deterministic, trends. That is, they may have a “unit root”. In such cases, model residuals do not have the properties needed for valid testing of hypotheses, even if data series are detrended. What is needed, then, is a testing procedure which distinguishes between deterministic time trends and unit roots in data.

Standard asymptotic theory cannot be used to test for unit roots in series which are non-stationary.[3] Fuller (1976) demonstrated that conventional testing procedures will be biased towards accepting stationarity when data are generated by a random-walk-type process. Dickey and Fuller (1979) derive the limiting distributions of the test statistic for the case where the null hypothesis is a unit root, and provide tables of critical values for the test statistic. This test, and two others, developed by Stock and Watson (1988), and Dickey and Pantula (1987) are applied to the series used in the model estimation and testing reported here. Further details of the tests, together with the results, are given in Appendix A.

On the basis of the test results, which suggested the presence of unit roots, all the data on indicators of activity and financial aggregates were first-differenced. The evidence for deterministic trends in addition to unit roots was weaker; hence the tables in the body of this paper report results from models estimated with differenced data only[4].

For the most part, first-differencing the data is consistent with the approach taken in BMS, where quarterly percentage changes were used for most variables[5]. The exception is that in most of the results reported in this paper, the short-term interest rate has also been differenced, whereas the level was used in BMS.

Footnotes

Consider the process: Under the null hypothesis that ρ = 1, (as in the case of one unit root), the usual formula for the large-sample variance of the least-squares estimator (1−ρ2)/T gives a value of zero for the variance of ρ when the true variance is non-zero. Applying conventional asymptotic theory to this type of model would clearly give misleading results. Thus usual least-squares techniques and ‘t’-tests for the value of ρ are not valid. [3]

Subsidiary tests were conducted in which the affected series were first detrended by regressing the first-differenced series on a constant and a first or second-order time trend, and the residuals from those regressions were then used in estimation. This change makes little difference to test results, which are available from the authors on request. [4]

It should be noted, of course, that this sort of specification ignores the potential long run relationships between the levels of the time series. Series may be “cointegrated”, that is, they may “trend together”. But it is not the purpose of this paper to pursue that issue. For a discussion of cointegration, see, inter alia, Engle and Granger (1987). [5]