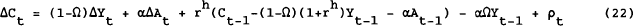RDP 8808: Consumption and Permanent Income: The Australian Case 3. Empirical Results
October 1988
- Download the Paper 865KB
a. Data
Each equation is estimated using real per capita data. All quarterly data (except the financial data used in estimating equation (19)) are seasonally adjusted, except where noted. Data sources are provided in the Appendix B.
For consumption, a series for the flow of services from consumer durables was constructed. The flow of services is defined to be equal to the rental services provided by the stock of durables, where those services are calculated as the rate of depreciation plus the real rate of return. Data for the stock of durables are constructed using data for expenditure on durables, and estimated depreciation rates. Further details of these series are provided in the Appendix.
For aggregate non-human wealth, a series was constructed using the data of Piggott (1986), Horn (1988), Adams (1987), and Helliwell and Boxall (1978). Further details are provided in the Appendix.
Before estimating the different equations, we need to take account of the time series properties of C and Y. In Appendix A we discuss and test the consumption and real household disposable income data for non-stationarity. Using the Augmented Dickey-Fuller test, we find that it is difficult to reject the hypothesis that both series are integrated of order one (i.e. they both have a unit root). We also find that they appear not to be cointegrated although this evidence is not strong and is inconsistent with an alternate test suggested below.
b. The Hall, Campbell, Mankiw Approach
As described in Section II, this approach involves estimating equation (19), repeated here for convenience.
Since changes in current income will usually lead to changes in perceptions about permanent income, ΔYt will usually be correlated with the unobserved µt. Accordingly, it would be expected that estimates of Ω will be biased downwards if OLS estimation is used. To avoid this problem, instruments must be used for ΔYt using variables which are uncorrelated with µt. Under the assumption of rational expectations, this will usually be satisfied by variables in the information set at time t−1, though as Campbell and Mankiw point out, there may be cases where variables from period t−2 will be more appropriate.
The use of instruments also requires that the instruments be correlated with ΔYt. If ΔYt is not well explained by the instruments, then Ω will not be estimated with precision. The results in Appendix A suggest that it will be difficult to find instruments for ΔYt.
First, we assume γ=1 and use the tests in Campbell and Mankiw (1987). Table 1 shows OLS and instrumental variable estimates for Equation (19) using quarterly data. The variables chosen as instruments for income are variables which are sometimes suggested as being useful in explaining income. They include lagged information on income, consumption, interest rates and monetary aggregates. (Changes in stock prices were also used as instruments but were found to be even worse as explanators of ΔYt.) Each equation is estimated over the period 1962(1)–1987(2), as well as two sub-periods, 1971(2)–1980(3) and 1980(4)–1987(2). The last period corresponds to the period in which interest rates have largely been deregulated.
| 1962(1)–1987(2) | 1971(3)–1980(3) | 1980(4)–1987(2) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Instruments(a) | R2 for ΔY | 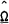 |
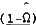 |
R2 for ΔY | 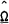 |
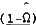 |
R2 for ΔY | 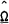 |
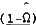 |
| None (OLS) | – |
.8174* (.0307) |
.1826* |
– |
.8321* (.0452) |
.1679* |
– |
.7605* (.0561) |
.2395* |
| ΔY | .0330 |
.9791* (.1910) |
.0209 |
.0974 |
.8050* (.1457) |
.1950+ |
.2131+ |
.8880* (.1334) |
.1120 |
| ΔC, ΔY | .0462 |
.8567* (.1439) |
.1433 |
.1739 |
.7497* (.1135) |
.2503* |
.3287 |
.8012* (.0988) |
.1988+ |
| Δ nom M, ΔY | .0978 |
.7753* (.0991) |
.2247* |
.2526 |
.7506* (.0941) |
.2494* |
.3579 |
.8861* (.1027) |
.1139 |
| Δ real M, ΔY | .0764 |
.8463* (.116) |
.1537+ |
.1991 |
.7307* (.1084) |
.2693* |
.3711 |
.8429* (.0959) |
.1571+ |
| Nom R, ΔY(b) | .2152+ |
.7879* (.0756) |
.2121* |
.2140 |
.8686* (.0987) |
.1314+ |
.4853+ |
.7727* (.0806) |
.2273* |
| Real R, ΔY(b) | .1263 |
.8080* (.0984) |
.1920+ |
.1991 |
.7307* (.1084) |
.2693* |
.4633+ |
.8035* (.0833) |
.1965* |
(a) Four lags of each variable were used as instruments in each
case. |
|||||||||
The OLS estimates for Ω, even though they should be biased towards rejecting the permanent income hypothesis, suggest that a substantial proportion of consumption is explained by the permanent income hypothesis.
For the instrumental variables estimates, it proved difficult to find variables which explained household income well. As can be seen in columns 2, 5 and 8 in Table 1, of the 18 estimates, only 4 sets of instruments could explain ΔYt at the 25 per cent significance level. As a result of these problems it is to be expected that Ω will not be estimated with a great degree of precision. On the other hand, it is likely that the instruments for ΔYt will be uncorrelated with µt.
As can be seen in columns 3, 6 and 9 in Table 1, the instrumental variable estimates for Ω were all significantly different from zero at very low significance levels. Estimates for (1 – Ω) can also be derived from these estimates. As can be seen in columns 4, 7 and 10, the estimates for (1 – Ω) are all smaller than the estimates for Ω, but in 8 cases were significantly different from zero at the 5 per cent level, and in another 6 cases were significantly different from zero at the 25 per cent level. In only 4 out of 18 cases were the estimates for (1 – Ω) not significantly different from zero at this wider level of significance.
Similar results were obtained when the dependent variable was derived from data on consumption expenditures. These showed estimates of Ω which were significantly different from zero, and estimates of (1 – Ω) which were often also significantly different from zero. The estimates for Ω appeared, however, to be slightly higher for the data on pure consumption, implying that the life-cycle hypothesis is more likely to be accepted when consumption is measured on a basis that is more appropriate given the theoretical model.
A further test of the permanent income hypothesis is the strong form of the test suggested by Hall (1978). That is, any other variable in the information set It, should be insignificant if included in the regression equation. For this test we regressed the residuals from each of the instrumental variables estimates of Table 1 against a number of the other variables. The results, which are not shown here, indicated that none of the other variables could explain the residuals from equation (15). This can be interpreted as evidence to support the permanent income hypothesis, and the assumption of rational expectations.
Table 2 shows the results when Equation (19) (with the constraint γ=1) is estimated using annual data for the period 1962/63 to 1986/87. The results using instruments vary relative to the results from the quarterly data (though the OLS estimate for the annual data does appear to be substantially more biased than for the quarterly data). There is still substantial variation among the estimates for Ω, but all are significantly differed to zero. Furthermore, the estimates for (1−Ω) tend again to be significantly different to zero, lending further credence to the notion that current income is also an important determinant of consumption.
| Instrumentsa | R2 for ΔY | 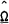 |
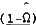 |
|---|---|---|---|
| None (OLS) | – |
.2854* (.0582) |
.7146 |
| ΔY | .0322 |
.7940* (.3251) |
.2060 |
| ΔC, ΔY | .0620 |
.5724* (.2660) |
.4276+ |
| Δ NomM, ΔY | .2840+ |
.6391* (.1132) |
.3609+ |
| Δ NomRb, ΔY | .2805+ |
.4811* (.1467) |
.5189+ |
Now consider the results when we drop the assumption that γ=1 although we still assume a constant r and therefore a constant γ.
An illustrative result using lagged changes in money and income as instruments is presented in Table 3. As can be seen from this result, γ is significantly less than 1 although this does not greatly affect the result for Ω which is marginally higher than the corresponding result in Table 1.
| Instruments | R2 for ΔY | 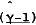 |
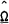 |
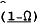 |
|---|---|---|---|---|
| Δ nom M, ΔY | .0978 |
−.0125* (.0041) |
0.8067* (.1049) |
0.1933 |
To provide some additional support for our earlier results that C and Y were non-stationary but apparently not cointegrated we can perform some stationarity tests on the residuals from Table 3. We used the Augmented Dicky-Fuller Test discussed in Engle and Granger (1987). The residuals from estimating equation (19) were differenced and regressed on the first lag and four lagged differences. The coefficient on the lagged residual was −0.986 with a t statistic of −3.6. This is significant using the criterion in Engle and Granger (1987) (Table 2), which indicates that the residuals are stationary. Therefore, either both C and Y are stationary or they are co-integrated. This suggests a possible problem with the power of the test of co-integration in the Appendix. It also implies that the co-integrating co-efficient is 0.8 which is close to that found in the more conventional test given in Appendix A.
To test the consequence of the assumption that r is constant, we assume 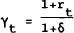 and
re-estimate equation (19).
and
re-estimate equation (19).
Table 4 shows the results when the estimates for equation (19) are modified by assuming a variable real rate of return. In this case, we assume a log utility function and make γ a function of rt and a constant rate of time preference δ. The expected real rate of return is proxied by the 90-day bank bill rate in the previous quarter less the inflation rate in the year to that quarter (Estimates using only one set of instruments are reported here but other results were quite similar also.) As can be seen the estimate for Ω is little different under the assumption of a variable rate of return.
| Instruments | 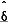 |
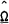 |
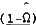 |
|
|---|---|---|---|---|
| a. Two lags of each variable were used as instruments in each case. b. The bill rate on 90-day bank accepted bills is used after 1969; prior to that a proxy is used. *+ Denote significant at the 5 and 25 per cent levels using t tests for parameter estimates and F tests for goodness of fit. |
||||
| Equation (19)(γ=1) | ΔNomM, ΔY | – |
.7753* (.0991) |
.2247* |
Equation (19) 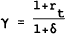 |
ΔNonM, ΔY |
.0225* (.0075) |
.7565* (.1047) |
.2435* |
Furthermore, the estimate for δ, the rate of time preference, appears plausible at around 2.3 per cent per quarter. Estimates for the various sub-periods also gave similar results for Ω (though estimates for δ were less precise), leading us to conclude that the assumption of a constant r does not have a major effect upon estimates for Ω.
Overall, the results obtained from the various quarterly and annual estimates appear to be quite consistent. They suggest the interpretation that aggregate consumption can be explained by the permanent income hypothesis, but that allowance should be made for a small but significant share of consumption which is better explained by current income.
c. The Hayashi Approach
Because movements in income are likely to be correlated with movements in wealth, equation (22) is estimated simultaneously with an equation explaining real wealth. The system of equations is:
Equation (23) is now assumed to be stochastic (deviating from the theoretical model) reflecting
measurement errors in the data. As mentioned above, we can make various assumptions about the
relationship between rh, and r as well as their variability. Firstly, we assume that
r=rh and both are constant which implies we can make r another parameter to be
estimated. The restriction can be tested. We then assume a variable rt and a constant
rh and finally a variable 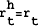 .
.
The equations are estimated using annual data and the SYSNLIN program in SAS. Instrumental variables are used in both equations. The choice of instruments is somewhat arbitrary. The variables used were a constant, a time trend, and five variables similar to those suggested by Hayashi (described in the Appendix), though in the event the results did not appear to be especially sensitive to the choice of the instruments.[6]
The estimates for the system of equations (22) and (23) with r=rh are shown in Row 1 of Table 5. The estimation period is too short to test the stability of the equation with any great degree of power, though shortening the sample period at either end had little impact on the parameter estimates. The equations show no signs of autocorrelated residuals. We therefore do not need to follow the procedures suggested by Hansen (1982) for calculating corrected standard errors. All three parameters were of the expected sign and were highly significant. The real rate of return is estimated to be 4.3 per cent per annum, which appears a plausible value. The value for α, 0.021, represents the proportion of total wealth consumed each year. This may be a little less than some might expect (see e.g., Modigliani 1987). Given the evidence that bequests are significant (see again, Modigliani, 1987), it does not seem implausible that this should be reasonably low. Another reason for a lower than expected value would be if (as Simes and Horn, 1986, conjecture), Australian data for aggregate non-human wealth overstate the true level.
| Restrictions |  |
 |
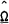 |
Autocorrelation Coefficients |
Minimised Objective Fn. |
|
|---|---|---|---|---|---|---|
| Eqn (22) | Eqn (23′) | |||||
| 1 None | .0212* (.0058) |
.0427* (.0054) |
.6081* (.0868) |
−.1046 (−.2151) |
.2248 (.2155) |
1.0952 |
| 2 Ω=1 | .0212* (.0058) |
.0415* (.0060) |
1 – |
.2251 (.2876) |
.2232 (.2157) |
1.3546 |
| 3 Ω=0 | – – |
.0415* (.0064) |
0 – |
.3342 (.2002) |
.2204 (.2160) |
1.1787 |
| 4 None (original (data) |
.00211* |
.0415* (.0069) |
.4946* (.0060) |
−.1989 (.1115) |
.2276 (−.2160) |
1.1163 (.2147) |
The estimate for Ω, of 0.61 is significantly different from zero (using the asymptotic t-test) and can be interpreted as indicating that a large proportion of consumers conform to the behaviour that is postulated by the life-cycle hypothesis. The implied estimate for (1 – Ω) is 0.39, which using the estimated standard error is also significantly different from zero. This would suggest that a smaller yet significant proportion of total consumption is explained by current disposable income. This could be explained, within the framework of the life-cycle hypothesis, either by liquidity constraints or by a high rate of time preference. The first explanation relies upon agents being either unable to borrow, or facing different lending and borrowing rates which precludes the use of capital markets to optimise their consumption path. The second explanation relies simply upon some consumers having very short planning horizons. As Hayashi (1985) points out, however, it is difficult to devise a test to ascertain the particular cause of this type of behaviour.[7]
More formal tests of the hypothesis of two types of consumption are provided in Rows 2 and 3 of Table 5. Here we test the restrictions that Ω=1 and Ω=0. Row 2 shows the results when the equations are estimated constraining Ω to unity. Analagous to a likelihood ratio test, we can take the difference in the sum of squared residuals from the constrained and unconstrained regression and compute a chi-squared test on the restriction. The test indicates that the restriction can easily be rejected. Row 3 shows the results when the equations are estimated constraining Ω to zero, i.e., assuming that consumption is purely explained by current income. This hypothesis can be also rejected. These two results indicate that the hypotheses of two distinct groups of consumers cannot be rejected.
Row 4 of Table 5 presents the results using consumption expenditures data rather than the pure consumption measure. The estimate for Ω, of 0.49, is significantly different from zero, indicating that the permanent income cannot be rejected. However, the estimate for (1 – Ω), of 0.51, is also significant, suggesting that permanent income hypothesis is less important for data on expenditures than for the pure consumption series. This finding is similar to Hayashi's (1981) finding for the U.S. case, and our own finding in the tests of the previous section.
The preceding estimates and discussion have focussed upon the results for the structural equations under the assumption that the discount rate that is used in calculating human wealth (rh) and the real interest rate (r) are constant and equal. Table 6 shows some estimates where these assumptions are relaxed. Row 1 shows the results described above where r and rh were assumed constant and equal. Row 2 shows the results when the assumption that r and rh are equal is relaxed. As can be seen, the estimates for r and rh are quite similar, through rh is estimated to be less than r, which seems a little counter-intuitive. However, rh is estimated with less precision than r, which is not surprising giving the low number of degrees of freedom, and the hypothesis that rh and r are equal cannot be rejected using the chi-squared test.
| Restrictions |  |
 |
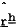 |
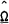 |
Minimised Objective Function |
|
|---|---|---|---|---|---|---|
| 1 | r = rh |
.0212* (.0058) |
.0427* (.0054) |
.0427* (.0054) |
.6081* (.0868) |
1.0952 |
| 2 | r constant, rh constant |
.0025 (.0086) |
.0418* (.0074) |
.0237* (.0086) |
.6120* (.0914) |
1.0627 |
| 3 | rt = 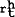 |
−.0058 (.0208) |
– |
– |
.0490 (0.1316) |
0.4012 |
| 4 | r variable, rh constant |
−.0043* (.0089) |
– |
.0183* (.0067) |
.6117* (.0933) |
0.3759 |
* denotes that parameter estimates are significantly different to zero using asymptotic t test at 5 per cent level. |
||||||
Rows 3 and 4 show the results when r is allowed to be variable. Here the actual values of rt were used in the estimation, where rt was the (ex post) real interest rate. Row 3 shows the results when the discount rate is constrained to equal the real interest rate. In this case Ω, the proportion of the population that consumes their permanent income is insignificantly different from zero. Row 4 shows the results when the discount rate is held constant. Here the estimate for Ω, 0.61 is very similar to the estimates of rows 1 and 2.
It should be noted that these experiments varying the rate of interest assume that α, the proportion of wealth consumed remains constant which is only true for a small class of utility function. Overall, these results suggest that the assumption of a constant discount rate used to calculate human wealth is reasonable given the maintained hypothesis of the model and does not seem to affect the share of consumption that is driven by permanent income.
Footnotes
It should be noted it did prove possible to find instruments which explained annual consumption well. If the problems with the quarterly series were due to noise in the data, it would be expected that annual data will be less affected. [6]
As an experiment, we attempted to model the parameter Ω as a function of nominal interest rates. If liquidity constraints are important we would expect that this variable would be negatively related to interest rates, approaching unity at times when borrowing was cheap, and falling at times when borrowing was costly. We found some evidence to support this conjecture, but the estimates did not appear to be particularly stable. [7]