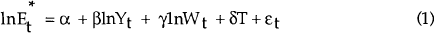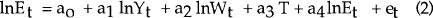RDP 8806: Employment, Output and Real Wages 4. Employment Output and Real Wages Revisited
September 1988
- Download the Paper 974KB
(a) The Specification
This section reports the results of estimating the relationship between employment, output and real wages over the period 1969(3)–1987(4). The approach to estimation is eclectic. Qualitative issues such as the implications of the estimated coefficients for the functional form of the underlying production function are not considered.
The standard specification used in empirical analysis of employment is based on an equilibrium employment equation of the form:
| where, | ||
| E* | = desired employment | |
| α | = constant | |
| Y | = output | |
| W | = real wage per efficiency unit of labour | |
| T | = time trend. |
This equation can be derived in a number of ways and from a number of production technologies. To estimate equation 1, a Koyck lag is generally imposed, yielding:
| where, | ||
| a0 | = α(1−λ) | |
| a1 | = β(1−λ) | |
| a2 | = γ(1−λ) | |
| a3 | = δ(1−λ) | |
| a4 | = λ | |
| λ | = adjustment parameter |
Equation 2 forms the basis of the results reported below. It should be noted that the dynamics imposed by the Koyck specification are very restrictive. To avoid imposing unnecessary restrictions on the data, equation 2 was tested against two less restrictive specifications. The results (reported in Appendix 1) show that the restrictions imposed by the Koyck specification could not be rejected.
(b) Data and Results
There are a number of series that can be used to measure employment. In our work, we have estimated the equations using both full-time employment and hours worked as the measure of employment. Total employment (part-time plus full-time) was not used because factors other than output and real wages have been very important in explaining developments in part-time employment.
There is also a variety of real wage measures which could be used. Most authors prefer to use either real average weekly earnings (RAWE) or a measure of real unit labour costs (RULC). In initial estimation, it was found that RAWE performed poorly. This is probably due to the fact that RAWE does not capture the effect of movements in non-wage costs and that secular influences, such as the growth in the relative importance of women in the labour force, have had a greater effect on AWE than other measures of wages.
When using RULC, allowance had to be made for the fact that, because this variable is related to productivity movements, it may be collinear with the output term. For this reason, an instrument for RULC was created by using an eight-period moving average productivity term as the denominator in RULC. This should largely eliminate cyclical influences on the RULC measure and hence reduce any multicollinearity between GDP and this measure of wages.
The results which are reported below use this measure of RULC. A comparative equation, using another measure of real wages as the explanatory variable,[4] can be found in Appendix 2.
The results of estimating equation 2 using quarterly data from 1969(3)–1987(4) are reported in Table 2.
| Variable | Coefficient | Standard Error |
|---|---|---|
| aO | 0.86 | 0.31 |
| lnYt | 0.12 | 0.03 |
| lnWt | −0.11 | 0.02 |
| lnEt−1 | 0.82 | 0.04 |
| T | −0.0005 | 0.0002 |
| Sample: 1969(3)–1987(4) | ||
| RBAR2 = 0.99 SEE= 0.045 SSR = 0.0013 | ||
| h = 0.17 Q(24) = 29.86 | ||
Each of the variables is significant and of the expected sign. The output and real wage elasticities are of the same order of magnitude, though of opposite sign. The long-run output elasticity is 0.65 while the long-run real wage elasticity is −0.61. These elasticities are within the range of previous Australian studies. The mean lag of the equation is around 18 months.
When total hours worked is used as the dependent variable, the results are as in table 3.
| Variable | Coefficient | Standard Error |
|---|---|---|
| aO | 2.07 | 0.74 |
| lnYt | 0.18 | 0.06 |
| lnWt | −0.21 | 0.04 |
| lnEt−1 | 0.76 | 0.06 |
| T | −0.0009 | 0.0004 |
| RHO | −0.44 | 0.12 |
| Sample: 1969(3)–1987(4) | ||
| RBAR2 = 0.91 SEE = 0.013 SSR = 0.0014 | ||
| h =−0.91 Q(24) = 31.96 | ||
Once again, each of the variables is significant and of the expected sign. The main difference in using total hours worked rather than full-time employment as the dependent variable is in the dynamics. Adjustment of total hours worked to its desired level is faster than that of full-time employment. This is plausible because employers can and do adjust hours worked before numbers employed (for example, by varying the amount of overtime worked or the number of part-time and/ or casual staff.) Correspondingly, the short-run elasticities in the hours worked equation are larger than in the full-time employment equation.
There was no evidence of instability in the preferred equation in Table 2. The sample was split at a number of points – at March 1978 at a time of a break in the employment series, and at the beginning of the Accord period. The null hypothesis of parameter stability could not be rejected at either point. The F-statistics for the 1978 split and the 1983 split were 0.74 and 1.21, respectively.
A number of qualifications to the results need to be acknowledged. The first is that labour is assumed to be the only input in the production process. A richer specification would include capital and intermediate inputs. If these variables were included in the production function, then the estimating equation should be extended to include the costs of capital and intermediate inputs. A number of estimations that included measures of these costs were conducted. Though not reported here, the results showed these variables were not statistically significant.
It should also be noted that the real wage is treated as exogenous. This assumption is open to question, with some authors claiming that the real wage is endogenous. If this is the case, a bias may exist in the reported estimates. However, the bias is, a priori indeterminate. This issue is recognised but has been ignored to date.
Footnote
This measure, real labour costs, is defined as non-farm wages, salaries and supplements plus payroll and fringe benefit tax deflated by the non-farm GDP deflator. This is the numerator of the RULC series. [4]