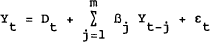RDP 8803: Do Financial Aggregates Lead Activity?: A Preliminary Analysis 4. Empirical Analysis for Australia
January 1988
- Download the Paper 695KB
The empirical work for Australian aggregates reported here is directed toward the question of how money and credit are related to measures of nominal economic activity, such as private demand and non-farm GDP. Specifically, whether a clear lead/lag relationship between money, credit and the indicators of nominal activity can be defined. The general tenor of the results is that monetary and credit aggregates move with, or may lag, movements in activity, and hence are more likely to be driven by nominal activity than to drive it.
a. Graphical Comparisons
A simple graphical analysis is a useful preliminary to the econometric analysis of the relationship between financial aggregates and activity. Of particular interest is whether monetary and credit aggregates have been a good guide to the direction of growth in spending, and particularly whether they have helped to predict turning points in spending. Figure 1 shows annual growth rates of credit[2], broad money and nominal private final expenditure (PFE). (The broader financial aggregates have been least affected by deregulation.) The vertical lines indicate major turning points in spending.
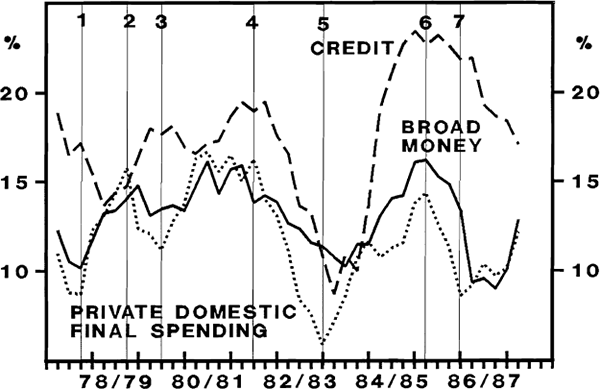
There is some discretion involved in locating a turning point. The episode labelled “4”, for example, might be disputed since the actual peak growth in spending was a year earlier. But the decisive change in the trend took place in December 1981, and it is that point which has been labelled as a turning point.
There are seven major turning points:
- in episode 1 (March 1978), growth in broad money picked up at the same time as growth in spending. Growth in credit picked up after a lag of two quarters;
- in episode 2 (March 1979), broad money lagged by one quarter, and credit by two quarters;
- in episode 3, (December 1979), broad money led by one quarter. Credit growth turned up slightly at the same time as spending, but then moved oppositely to spending over the next two quarters. This is best scored as “no result”;
- episode 4 (December 1981) appears at first to show broad money leading activity. But this could be disputed, since the downturn in December 1981 could be the lagged effect of the short-lived fall in spending occurring in the previous quarter. The rise in broad money growth in March 1982 supports the latter view. This is scored “no result”. The major downturn in credit clearly lagged by a quarter;
- episode 5 (June 1983) saw spending turn up one quarter before credit, and two quarters before broad money;
- in episode 6 (September 1985), broad money would best be judged as coinciding with spending. A case could be made for credit showing a lead, but this is tenuous. In December 1985, the figure for growth in credit would have been a poor guide to the direction of growth in spending. This is scored as a lag for credit; and
- in the last episode (June 1986), broad money growth turned a quarter later than growth in spending. Simultaneously, credit growth steadied, but then continued to fall. Based on this graph, credit was a poor indicator of spending over 1986–87.
Table 1 shows a “scoreboard” from the above episodes. Broad money was coincident twice. It led once, and lagged three times, with another episode which could go either way. Credit was almost always a lagging indicator.
| Broad Money | Credit | |||||
|---|---|---|---|---|---|---|
| lead | coincident | lag | lead | coincident | lag | |
| 1 (Mar. 1978) | X | X | ||||
| 2 (Mar. 1979) | X | X | ||||
| 3 (Dec. 1979) | X | ? | ? | ? | ||
| 4 (Dec. 1981) | ? | ? | ? | X | ||
| 5 (Jun. 1983) | X | X | ||||
| 6 (Sep. 1985) | X | X | ||||
| 7 (Jun. 1986) | X | X | ||||
Figure 1 gives some feel for how the two of the major financial aggregates relate to a measure of activity. But there are other measures of activity and many other aggregates. It would be tedious to present all possible combinations graphically, and there are dangers of subjective interpretation of graphs.
The following sections report more formal statistical tests of lead/lag relationships for a number of aggregates and measures of activity.
The financial aggregates considered are:
- M3 and broad money, the two monetary aggregates which receive most attention;
- borrowings by non-bank financial institutions, the major non-M3 component of broad money;
- lending by all financial intermediaries; and
- credit.
The indicators of activity are nominal non-farm GDP (GDPNF) and nominal private final expenditure (PFE). Measures of real GDPNF and PFE and their price deflators are also included in the VAR analysis.
b. Correlation Results
Simple bivariate correlation coefficients were estimated between quarterly log changes and annual rates of growth of aggregates and measures of nominal activity. Growth rates of financial aggregates were adjusted, where appropriate, for transfers when NBFIs became banks and for other breaks in the data series. (Data sources and construction details are outlined on pages 23 and 24 of the paper.)
The results of estimating correlations between 12 months-ended rates of growth and quarterly log-changes are summarised in Tables 2 and 3 respectively. An *(**) appears where coefficients are significantly different from zero at the five per cent (one per cent) level. A dash (-) appears where the estimated coefficient was not significantly different from zero.
The main point of interest in these sample coefficients is whether lagged values of one variable are significantly correlated with current values of another. A significant sample correlation coefficient is taken as an indication that the lagged variable leads the current variable. In the tables, either of the following results would be of interest:
- asterisks only along the first row of each section, which would indicate that lags of the activity variable are correlated with the current value of the financial variable;
- asterisks only down the first column of each section, which would indicate that lags of the financial variable are correlated with the current value of the activity variables.
The results in Table 2 show that lagged values of annual growth in non-farm GDP and PFE tend to be significantly correlated with current values of all financial aggregates (except perhaps M3). By contrast, few lags of the annual growth in financial aggregates are significantly correlated with current values of GDPNF and PFE, and these are restricted to the monetary, rather than credit, aggregates.
| Annual ΔGDPNF | ΔGDPNF(−1) | ΔGDPNF(−2) | ΔGDPNF(−3) | Annual ΔPFE | ΔPFE(−1) | ΔPFE(−2) | ΔPFE(−3) | ||
|---|---|---|---|---|---|---|---|---|---|
| Annual | ΔBM | ** | ** | ** | * | ** | ** | ** | ** |
| ΔBM(−1) | * | ** | |||||||
| ΔBM(−2) | – | * | |||||||
| ΔBM(−3) | – | – | |||||||
| Annual | ΔM3 | ** | * | – | – | * | – | – | – |
| ΔM3(−1) | ** | – | |||||||
| ΔM3(−2) | – | – | |||||||
| ΔM3(−3) | – | – | |||||||
| Annual | ΔNBFI | * | ** | ** | – | ** | ** | ** | – |
| ΔNBFI(−1) | – | ** | |||||||
| ΔNBFI(−2) | – | * | |||||||
| ΔNBFI(−3) | – | ||||||||
| Annual | ΔAFIC | – | * | * | * | – | * | ** | * |
| ΔAFIC(−1) | – | – | |||||||
| ΔAFIC(−2) | – | – | |||||||
| ΔAFIC(−3) | – | – | |||||||
| Annual | ΔAFIL | – | * | ** | * | ** | ** | ** | ** |
| ΔAFIL(−1) | – | – | |||||||
| ΔAFIL(−2) | – | – | |||||||
| ΔAFIL(−3) | – | – | |||||||
|
* indicates positive correlation significantly different from zero at the 5 per
cent level. |
|||||||||
Current period growth in the three borrowings aggregates is significantly correlated with current period growth in both activity variables. Credit is not contemporaneously correlated with either activity variable.
On balance, this evidence weighs in favour of the view that the financial aggregates move with, or lag, activity variables. The case for a lagged response is strongest for credit.
Table 3 shows equivalent correlations between quarterly changes. The overall level of correlation is weaker than the annual growth data, but such significance as there is tends to come from lags of activity moving with current changes in financial aggregates. Only broad money is contemporaneously correlated with the activity variables. Again, M3 appears to have the weakest relationship with the activity variables.
| Quarterly ΔGDPNF |
ΔGDPNF(−1) | ΔGDPNF(−2) | ΔGDPNF(−3) | Quarterly ΔPFE |
ΔPFE(−1) | ΔPFE(−2) | ΔPFE(−3) | ||
|---|---|---|---|---|---|---|---|---|---|
| Quarterly | ΔBM | ** | – | * | – | * | ** | – | ** |
| ΔBM(−1) | – | – | |||||||
| ΔBM(−2) | – | – | |||||||
| ΔBM(−3) | – | – | |||||||
| Quarterly | ΔM3 | – | – | – | – | – | – | – | – |
| ΔM3(−1) | – | – | |||||||
| ΔM3(−2) | – | – | |||||||
| ΔM3(−3) | – | – | |||||||
| Quarterly | ΔNBFI | – | – | ** | – | – | ** | * | ** |
| ΔNBFI(−1) | – | – | |||||||
| ΔNBFI(−2) | * | – | |||||||
| ΔNBFI(−3) | – | – | |||||||
| Quarterly | ΔAFIC | – | – | * | – | – | – | * | * |
| ΔAFIC(−1) | – | – | |||||||
| ΔAFIC(−2) | – | – | |||||||
| ΔAFIC(−3) | – | – | |||||||
| Quarterly | ΔAFIL | – | – | * | – | – | – | * | ** |
| ΔAFIL(−1) | – | – | |||||||
| ΔAFIL(−2) | * | – | |||||||
| ΔAFIL(−3) | – | – | |||||||
|
* indicates positive correlation significantly different from zero at 5 per cent
level. |
|||||||||
On the whole, the quarterly results also support the view that the financial aggregates move with, or lag, changes in nominal activity, and not the reverse.
The strength of such results based on simple bivariate correlations is nonetheless limited. A more general approach is to test whether a number of lags of financial variables jointly help to explain the current value of the activity variables and vice versa.
c. VAR Methodology
The results obtained from correlation analysis can be more thoroughly assessed using vector autoregression (VAR) techniques. VAR models are useful for testing one variable's power for predicting another variable at a very general level. Granger-causality tests can be used to clarify lead/lag relationships between variables.
A VAR model attempts to explain movements in a vector Yt of n endogenous variables. It is assumed that Yt is generated by the mth order vector-autoregression:
where Dt is a (nxl) vector representing the deterministic component of Yt(Dt is usually a polynomial in time: for the models reported here, Dt is a simple constant term, i.e., a polynomial of order zero), βj are (nxn) matrices of coefficients and εt is a (nxl) vector of multivariate white noise residuals.
VAR models are very general: unlike conventional regression equations, no restrictions are applied to the βj matrix. Consequently, the VAR model consists of n linear equations, with each of the n endogenous variables appearing as the dependent variable in one equation, and (m) lags of all n variables, plus the deterministic component, appearing on the right-hand side of every equation. Under the orthgonality conditions E(εt)=0 and E(Yt−j εt)=0, each equation can be estimated separately by ordinary least squares.
Once estimated, the models can be used to test whether one variable in the vector is useful in forecasting another variable from the vector. Variable Y1t is useful in forecasting variable Y2t if lags of Y1t in the equation for Y2t signficantly reduce the forecast error variance. In other words, if lags of Y1t are jointly significant in an equation for Y2t which also includes lags of Y2t as explanatory variables, then Y1t is said to “Granger-cause”[3] Y2t.
Put in the terms of the present exercise, if including lags of money or credit in the equation improves the prediction of spending over and above the contributions of lags of spending itself, then money or credit would be said to “cause” spending. Granger-causality can be tested using a standard F-test for the joint significance of lags of each variable.
“Causality” has a strictly defined, technical meaning when used in relation to VAR models. It does not necessarily have to imply causality in the usual sense. Nevertheless, if lags of variable Y1t are significant explanators of current values of Y2t, given the information already supplied by own-lags, then we can infer that Y1 leads movements in Y2.[4]
d. VAR Results
The VAR models were estimated using annual growth rates and quarterly log-changes in real and nominal GDPNF and PFE, the relevant price deflators, each of the five financial aggregates and yields on 90-day bank-accepted bills. Four different models were estimated for each financial aggregate: two models were estimated including the nominal activity variables and the interest rate, and another two with real activity variables and price deflators separately, together with the interest rate. Lag-lengths were chosen so that in most cases the last lags were jointly significantly different fron zero, and the errors free from serial correlation, within the constraint of degrees of freedom[5]. The test for correct lag-length is an F-test for the joint significance of the last lag of every explanatory variable in each equation in the system. This test was applied to each model in steps, beginning with a lag of order four and working downwards. The relatively small sample size (40 observations for the annual series), and the large number of estimated coefficients restricted lag length to lags of order three or four at most. Some models were estimated with second order lags, and no model had a lag order higher than four.
It was noted in Section 3 that some researchers' results were sensitive to the inclusion of interest rates in models of money and activity. The early studies by Sims (1972) and Williams, Goodhart and Gowland (1976), for example, did not include interest rates, and it has been noted that Sims (1980b) found substantial changes in the relationships when interest rates were included. No separate bivariate VAR tests of money and activity have been conducted for this study. Models which include interest rates provide, in our view, a more powerful test of the lead/lag relationship in question. Models which exclude variables which are relevant to the joint behaviour of money and activity may produce spurious results.[6] These variables were selected as giving a good coverage of the conventional financial aggregates and as consistent with the bulk of overseas studies.
A complete set of results of Granger-causality tests is reported in Tables 4–7. Tables 4 and 5 report results for annual growth, and Tables 6 and 7 refer to quarterly changes. An *(**) indicates that coefficients on lags of the relevant explanatory variable are jointly significantly different from zero at the five (one) per cent level. A dash (-) appears where the estimated coefficients are not significantly different from zero.
| Model 1 | Model 2 | |||||||
|---|---|---|---|---|---|---|---|---|
| Dependent Variables | Explanatory Variables | Dependent Variables | Explanatory Variables | |||||
| BM | Real GDPNF |
P | R | BM | Nom GDPNF |
R | ||
| BM | ** | – | – | – | BM | ** | – | – |
| Real GDPNF | – | – | – | – | Nom GDPNF | – | – | – |
| P | – | – | ** | – | R | – | – | * |
| R | – | – | – | * | ||||
| M3 | Real GDPNF |
P | R | M3 | Nom GDPNF |
R | ||
| M3 | ** | – | – | – | M3 | ** | – | – |
| Real GDPNF | – | – | – | – | Nom GDPNF | – | * | – |
| P+ | – | – | ** | – | R | – | – | ** |
| R | – | – | – | ** | ||||
| NBFI | Real GDPNF |
P | R | NBFI | Nom GDPNF |
R | ||
| NBFI | ** | ** | – | – | NBFI | ** | * | – |
| Real GDPNF | – | – | – | – | Nom GDPNF | – | ** | – |
| P+ | – | – | ** | – | R | – | – | ** |
| R | – | – | – | * | ||||
| AFIC | Real GDPNF |
P | R | AFIC | Nom GDPNF |
R | ||
| AFIC | * | * | – | – | AFIC | ** | – | – |
| Real GDPNF | – | * | – | – | Nom GDPNF | – | – | – |
| P | – | – | ** | – | R | – | – | * |
| R | – | – | – | – | ||||
| AFIL | Real GDPNF |
P | R | AFIL | Nom GDPNF |
R | ||
| AFIL | ** | ** | – | – | AFIL | ** | – | – |
| Real GDPNF | – | – | – | – | Nom GDPNF | – | * | – |
| P+ | – | – | ** | – | R | * | – | ** |
| R | – | – | – | ** | ||||
| Model 3 | Model 4 | |||||||
|---|---|---|---|---|---|---|---|---|
| Dependent Variables | Explanatory Variables | Dependent Variables | Explanatory Variables | |||||
| BM | Real PFE |
P | R | BM | Nom PFE |
R | ||
| BM | ** | * | – | – | BM | ** | * | – |
| Real PFE | – | ** | – | – | Nom PFE | – | ** | – |
| P | – | – | ** | – | R | – | – | * |
| R | – | – | – | * | ||||
| M3 | Real PFE |
P | R | M3 | Nom PFE |
R | ||
| M3 | ** | – | – | – | M3 | ** | – | – |
| Real PFE | – | ** | – | – | Nom PFE | – | ** | – |
| P | – | – | ** | – | R | – | – | ** |
| R | – | – | – | ** | ||||
| NBFI | Real PFE |
P | R | NBFI | Nom PFE |
R | ||
| NBFI + | – | * | – | – | NBFI + | – | ** | – |
| Real PFE | – | ** | – | – | Nom PFE | – | ** | – |
| P | ** | – | ** | – | R | – | – | ** |
| R | – | – | – | ** | ||||
| AFIC | Real PFE |
P | R | AFIC | Nom PFE |
R | ||
| AFIC | ** | ** | ** | – | AFIC | ** | * | – |
| Real PFE | – | ** | * | – | Nom PFE | – | ** | – |
| P | * | – | ** | – | R | * | – | ** |
| R | – | – | – | ** | ||||
| AFIL | Real PFE |
P | R | AFIL | Nom PFE |
R | ||
| AFIL+ | ** | ** | * | – | AFIL+ | ** | * | – |
| Real PFE | – | ** | – | – | Nom PFE | – | ** | – |
| P | * | – | * | – | R | * | – | ** |
| R | – | – | – | ** | ||||
| Model 1 | Model 2 | |||||||
|---|---|---|---|---|---|---|---|---|
| Dependent Variables | Explanatory Variables |
Dependent Variables | Explanatory Variables |
|||||
| BM | Real GDPNF |
P | R | BM | Nom GDPNF |
R | ||
| BM | – | – | – | – | BM | – | – | – |
| Real GDPNF | – | – | – | – | Nom GDPNF | – | – | – |
| P | – | – | * | – | R | * | – | ** |
| R | ** | – | – | ** | ||||
| M3 | Real GDPNF |
P | R | M3 | Nom GDPNF |
R | ||
| M3 | – | – | – | – | M3 | – | – | – |
| Real GDPNF | – | – | – | – | Nom GDPNF | – | – | – |
| P | – | – | – | – | R | – | – | ** |
| R | – | – | – | ** | ||||
| NBFI | Real GDPNF |
P | R | NBFI | Nom GDPNF |
R | ||
| NBFI | – | ** | – | – | NBFI | – | * | – |
| Real GDPNF | * | – | – | – | Nom GDPNF | – | – | – |
| P | – | – | – | – | R | – | – | ** |
| R | – | – | – | ** | ||||
| AFIC | Real GDPNF |
P | R | AFIC | Nom GDPNF |
R | ||
| AFIC | * | ** | – | – | AFIC | ** | * | – |
| Real GDPNF | – | – | * | – | Nom GDPNF | – | – | – |
| P | – | – | * | – | R | – | – | ** |
| R | – | – | – | ** | ||||
| AFIL | Real GDPNF |
P | R | AFIL | Nom GDPNF |
R | ||
| AFIL | * | * | – | – | AFIL | * | – | – |
| Real GDPNF | * | – | * | – | Nom GDPNF | – | – | – |
| P | – | – | * | – | R | – | – | ** |
| R | – | – | – | ** | ||||
| Model 3 | Model 4 | |||||||
|---|---|---|---|---|---|---|---|---|
| Dependent Variables |
Explanatory Variables |
Dependent Variables |
Explanatory Variables |
|||||
| BM | Real PFE |
P | R | BM | Nom PFE |
R | ||
| BM | – | – | – | – | BM | – | * | – |
| Real PFE | – | – | – | – | Nom PFE | – | – | – |
| P | – | – | – | – | R | – | – | ** |
| R | – | – | – | ** | ||||
| M3 | Real PFE |
P | R | M3 | Nom PFE |
R | ||
| M3 | – | – | – | – | M3 | – | – | – |
| Real PFE | – | – | – | – | Nom PFE | – | – | – |
| P | – | – | – | – | R | – | – | ** |
| R | – | – | – | ** | ||||
| NBFI | Real PFE |
P | R | NBFI | Nom PFE |
R | ||
| NBFI | – | – | – | – | NBFI | – | ** | – |
| Real PFE | – | – | – | – | Nom PFE | – | – | – |
| P | * | – | – | – | R | – | – | ** |
| R | – | – | – | ** | ||||
| AFIC | Real PFE |
P | R | AFIC | Nom PFE |
R | ||
| AFIC | ** | ** | ** | * | AFIC | * | – | – |
| Real PFE | – | – | – | – | Nom PFE | – | – | – |
| P | – | – | – | – | R | – | * | ** |
| R | * | – | – | ** | ||||
| AFIL | Real PFE |
P | R | AFIL | Nom PFE |
R | ||
| AFIL | – | – | * | – | AFIL | * | – | – |
| Real PFE | – | – | – | – | Nom PFE | – | – | – |
| P | – | – | – | – | R | – | – | ** |
| R | – | – | – | ** | ||||
The off-diagonal elements of these matrices are the most interesting, since those symbols indicate the Granger-causal relationships. Significant coefficients along the diagonal simply show that the dependent variable is explained by its own lags.
The relevant results from VAR analysis of annual growth in financial aggregates and activity are summarised below:
Annual Growth:
| Variable | Granger-caused by | |
| • | broad money: | Both real and nominal PFE |
| • | M3: | – |
| • | NBFI borrowings: |
Both real and nominal GDPNF Both real and nominal PFE |
| • | AFI credit: |
Real GDPNF Both real and nominal PFE |
| • | AFI lending: | Real GDPNF Both real and nominal PFE |
There was no instance of a financial aggregate “causing” nominal or real GDPNF or PFE. All financial aggregates, except M3, are “caused” by at least one activity variable. In three models, a financial aggregate significantly Granger-causes prices. However, in two of these instances, the financial aggregate is also significantly explained by lags of prices. These results are not easy to interpret, and probably point towards a contemporaneous relationship, which cannot be usefully examined in a VAR model.
The same test conducted with seasonally-adjusted quarterly changes generally support these conclusions, although the overall fit of the models is poorer, and the relationships are weaker. The following table summarises the quarterly results.
Quarterly Growth:
| Variable | Granqer-caused by | |
| • | broad money: | Nominal PFE |
| • | M3: | – |
| • | NBFI borrowings: |
Nominal GDPNF Nominal PFE |
| • | AFI credit: |
Both real and nominal GDPNF Real PFE |
| • | AFI lending: | – |
In two cases (NBFI borrowing and AFI lending) the financial aggregate “caused” real GDPNF at the five per cent level. In both of these cases there is also an opposite significant causality from real GDPNF to the financial aggregate, which implies that an unambiguous lead/lag relationship cannot be defined from these results.
The presence of serial correlation in some of the estimated equations on annual data also suggests caution (see Footnote 5). Nevertheless, the general tenor of the results clearly favours a lead relationship from activity to the financial aggregates (excluding M3).
Footnotes
Credit is defined as lending by financial intermediaries plus bank bills outstanding. See “Measures of Financing”, Reserve Bank of Australia Bulletin, October 1987, for further details. [2]
So-named after C.W.J. Granger, see Granger (1969). [3]
Some studies (including Friedman, 1981) use the innovation accounting techniques suggested in Sims (1980a) to analyse the timing and extent of causal relationships between macroeconomic variables. These techniques have not been employed in this analysis. One short-coming of such tests is that it is necessary to assume a causal ordering in the vector of endogenous variables before the techniques can be applied. The weakness of these techniques are discussed in Cooley and LeRoy (1985) and Trevor and Donald (1986). In regard to the Granger-causality tests applied in this analysis, Cooley and LeRoy argue that the Granger test cannot be interpreted as a test of predeterminedness or strict exogeneity. Strict exogeneity implies Granger-causality, but the converse is not true. Although not useful for proving causal orderings, it can be correctly applied in uncovering characteristics of the data to be explained by theory. On the basis of the limitations of the test, care needs to be taken in interpreting the results. [4]
Some of the equations estimated using annual growth data appear to have significantly correlated errors. These equations are marked with a + on Tables 4 and 5. These correlation problems could not be overcome by extending the model lag length within the degrees of freedom constraint. The majority of equations, however, were free from serial correlation at the 5 per cent level of significance. [5]
It has been pointed out that for an open economy, the exchange rate may be a key factor in the relationship of the financial system to economic activity. Strictly speaking, the most general of statistical tests would include the exchange rate as well as interest rates and financial aggregates. This is to be investigated in future work. [6]