RDP 8701: The Australian Demand Function for Money: Another Look at Stability 3. Testing for Stability: Some Issues
January 1987
- Download the Paper 958KB
Perhaps the most commonly-employed test for parameter variation within the sample is that originated by Chow (1960). This test has much to commend it – its simplicity, intuitive appeal, ease of computation and so on.
An objection to the Chow test in testing for parameter Instability is that the point of change in parameter values must be arrived at in some fashion based on prior knowledge or arbitrary Judgement. This problem can be handled by employing Quandt's (1960) likelihood-ratio technique to isolate the most likely point at which structural change may have occurred, and then applying the chow test at that point.
A second difficulty with the Chow test, and with any test in which the alternative hypothesis embodies a discrete change in parameter values at some point, is that change may be gradual rather than discrete. While in principle multiple break points could be allowed for, it Is preferable to employ techniques which cope with this possibility more effectively.
Accordingly, we supplement the Chow-type tests with the Cusum and Cusum of Squares techniques (hereafter called CUSUM and CUSUMSQ), outlined in Brown, Durbin and Evans (BDE, 1975). These tests, based on recursive residuals, are more suited to detecting gradual change. BDE's “homogeneity statistic”, based on the residual sum of squares from moving regressions over non-overlapping sub-samples, is also reported.
In addition to the above, however, a further issue needs to be addressed. Discussion of instability of the demand for money invariably centres around the co-efficients on the interest rate and income terms, and on the implied adjustment speed (see, for example, Judd and Scadding (1982)).
An issue not given much attention in the literature is the possibility of heteroskedastlcity in the residuals. This appears to be an important ommission. The increase in prediction errors of standard equations in the 1970's gained a good deal of attention. This may be due to changes in the slope parameters, but equally, it suggests that formal tests for non-uniformity of the error variance might be worth pursuing.
That said, it is of course worth noting that a change in the variance is itself a structural change, and an important one, particularly for policy purposes. For it means that a monetary policy based on even very good knowledge of the demand function for money must be conducted with less precision and certainty.
Table 5 presents evidence that heteroskedastlcity cannot be ruled out. The equations are tested using Breusch and Pagan's (1979) test which involves checking for any relationship between the squared estimation residuals, appropriately scaled, and some set of exogenous variables.
For most of the models, it seems to be inappropriate to assume that the error variance is uniform throughout the sample. The only exception may be Pagan and Volker's (1980) equation.
A problem then arises in some of the test procedures discussed above. The CUSUMSQ statistic, for example, would most likely be affected. BDE (1975) show that this statistic is equivalent to SSRτ/SSRT, where SSRτ represents the sum of squared residuals from a regression on τ observations, and where the total sample length is T. This is just the ratio of the maximum likelihood variance estimators, for samples τ and T respectively, multiplied by the ratio τ/T. Where the error-variance is unchanging, therefore, the appropriate “centre-line” for the CUSUMSQ plot is the straight line defined by τ/T. Confidence intervals are developed for deviations of the CUSUMSQ statistic from this line. But where the error variance is changing, this centre-line and the associated confidence intervals will no longer be appropriate.
| Equation no: | Test * Statistic |
Critical Value | |
|---|---|---|---|
| 1% | 5% | ||
| SV-2 | 28.83 | 16.57 | 12.55 |
| SV-3 | 10.78 | 16.87 | 12.59 |
| PO-2 | 21.14 | 16.41 | 16.55 |
| PO-3 | 12.67 | 16.21 | 12.55 |
| FR-2 | 25.22 | 15.09 | 11.07 |
| FR-3 | 26.80 | 15.09 | 11.07 |
| PV-2 | 7.15 | 18.48 | 14.07 |
| PV-3 | 9.06 | 18.48 | 14.07 |
|
* The test proceeds by considering a regression model yt =
f(xt,β) + τt where
τt has mean zero, but the variance property |
|||
Similarly, there will be difficulties with the Chow test, since in testing the hypothesis that the parameter vectors are identical between two subsamples, it assumes that the variance of the residuals is unchanging between the two subsamples.
There is a small literature indicating that the Chow test is inappropriate in conditions of heteroskedasticity. Toyoda (1974) and Schmidt and Sickles (1977) addressed this question. A general conclusion to emerge from this work was that the true significance level of the test differs from the nominal level, when the error variance is not uniform. Jayatissa (1977) developed a test statistic free from this problem, but it tends to be computationally demanding, as well as suffering some other disadvantages (see Honda (1982)). A Wald test proposed by Watt (1979) is computationally easier, and work by Honda (1982) allows reasonable confidence that the asymptotic properties of the Wald test are not inferior to those of the Jayatissa test for sample sizes of over 60 observations, provided the break point is not too close to one end of the sample.
With the above points in mind, the next section proceeds to give results of a range of tests discussed above.
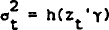 , where the zt are exogenous. If
we take the zt to be the xt in the original
regression, including a constant term, the null hypothesis is
that γ2 = γ3 = …
= γk = 0, where k is the dimension of γ. The test is
conducted by estimating the equation
, where the zt are exogenous. If
we take the zt to be the xt in the original
regression, including a constant term, the null hypothesis is
that γ2 = γ3 = …
= γk = 0, where k is the dimension of γ. The test is
conducted by estimating the equation 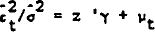 where
σ−2 is the estimated sample variance.
Denoting the regression sum of squares from this equation as RSS, under
H0, RSS/2 –
where
σ−2 is the estimated sample variance.
Denoting the regression sum of squares from this equation as RSS, under
H0, RSS/2 – 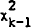 (asymptotically).
(asymptotically).