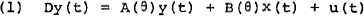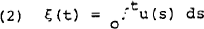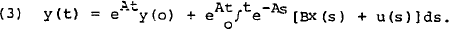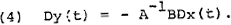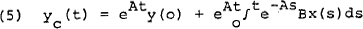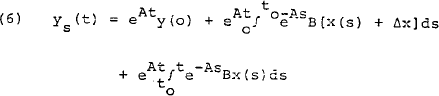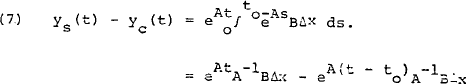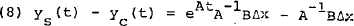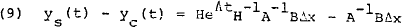RDP 7903: Monetary Rules: A Preliminary Analysis Appendix C: Technical Analysis
September 1979
The RBA79 model is estimated by a full information maximum likelihood technique using computer programs written by C.R. Wymer. Before estimating the model, it is linearised about a quasi steady state growth path. The linear version of the model is of the form:
where y(t) is a vector of G endogenous variables, x(t) is a vector of N exogenous variables and A and B are G x G and N x N matric whose elements are functions of a set of structural parameters. It is assumed that the non-zero elements of u(t) (some are zero since the corresponding equations are identities) are disturbances generated by a stationary process with a constant spectral density matrix so that the integral:
is an homogenous random process with uncorrelated increments. It may be shown that ξ(t) is non-differentiable and hence u(t) can not be defined rigorously. Nevertheless, u(t) may be treated as having the properties of a white noise disturbance.[18]
The general solution to the above differential equation system is:
If the eigenvalues of the matrix A all have negative real parts, the model will converge to the steady state path:
Thus, in the case of RBA79, where the variables are in terms of logarithms, and it is assumed that in the steady state the levels of exogenous variables follow exponential growth paths, the levels of endogenous variables will also follow exponential growth paths.
The control solution of the model may be obtained from equations (3) and (2) and by setting ξ(t) at its expected value of zero. Thus, the control solution, denoted yc(t), will be:
When the system given by equation (5) is given a constant exogenous shock Δx for the period t = 0 to t = to, the shocked values of the endogenous variables may be found by:
which, in terms of deviations from control is:
When the shock is sustained, equation (7) becomes:
which, if A can be diagonalised,[19] can be written as:
where H is a matrix whose columns are the eigenvectors of A, and A is a diagonal matrix whose diagonal elements are the eigenvalues of A.
When the real parts of these eigenvalues are negative ys(t) − yc(t) will converge to − A−1BΔx. Where the eigenvalues are complex (with negative real parts) the convergence path follows a damped cycle. The vector − A−1BΔx represents the permanent or steady state effect of the shock on the levels of the endogenous variables in the vector y(t). There is thus no permanent effect on the vector Dy(t) which, in the case of a model specified in logarithmic form, represents the rates of growth of the endogenous variables.