RBA Annual Conference – 2018 Discussion
- Download 239KB
1. Marcelle Chauvet[*]
Overview
The paper by Luke Hartigan and James Morley examines how the dynamics of the macroeconomy in Australia have changed since the inception of the inflation-targeting regime in the second quarter of 1993. It focuses on changes in the common components of real and nominal variables, and whether there is evidence of changes in the transmission of monetary policy shocks. The paper implements an analysis using factor models on a large panel of real and nominal variables (104 variables, 1976:Q4–2017:Q2), and explores the dynamics of the factor structure in detail. It takes into account several measures of potential change such as structural breaks, changes in volatility, changes in cross-correlations and changes in the transmission of monetary shocks. The paper uses three methods: i) exploratory principal components analysis to obtain the number of factors; ii) approximate dynamic factor models to estimate the factors and to test for potential breaks and stability of the factor loadings; and iii) factor augmented vector autoregressions (FAVAR) to examine potential changes in the transmission of monetary shocks.
The paper finds that Australian macroeconomic fluctuations are mostly captured by two common factors representing ‘real’ economic activity and the ‘nominal’ sector. Recursive estimation indicates a decline in the number of factors over time, which could be related to changes in cross-correlation or volatility in the factor structure associated with the inflation-targeting regime. In order to examine this further, the Han and Inoue (2015) structural break test is used to evaluate potential changes. The Lagrange multiplier (LM) statistic indicates a break in 1991:Q4, the Wald test in 1998:Q3. The paper notes that both tests are significant if the break occurred in 1993:Q1, around the time inflation targeting was implemented. The evidence points to changes in volatility rather than in the cross-correlation between variables.
The paper further investigates this possibility by studying the cross-section standard deviation of the common components and of the idiosyncratic components for the real and nominal sectors for: (i) all variables, (ii) for prices, and (iii) also for consumer price index (CPI) inflation. It finds a large reduction in the volatility of common components, including for CPI inflation, but not in the volatility of the noisy idiosyncratic components over time. This is particularly the case since the introduction of inflation targeting. This result suggests that monetary policy should target more persistent quarter-to-quarter changes rather than noisy oscillations, which can be separated out using the factor structure. The paper recursively estimates loadings of real gross domestic product (GDP), CPI inflation, and the overnight cash rate (OCR) on the factors, and finds that they stabilise over time rather than display sudden jumps. This result is, once again, consistent with changes in the volatility of the factors rather than with changes in cross-correlations related to the factor structure.
Finally, the paper uses FAVAR to examine the effects of inflation targeting on the transmission of monetary policy shocks, using the (rotated) first two factors and the interest rate represented by the OCR. For the full sample, contractionary monetary policy leads to a fall in the ‘real’ factor, the ‘nominal’ factor and, as expected, also in GDP growth and CPI inflation. In order to investigate potential changes in the transmission of monetary shocks, the Qu and Perron (2007) break test is applied to each equation of the FAVAR. The results indicate changes in the parameters in 1990 and around 2010–11, which coincides with the European debt crisis. Impulse response functions are then obtained for three sub-samples: before the inflation-targeting regime (1976:Q4–1993:Q1), during the first part of the regime (1993:Q2–2004:Q4), and for the latest part of the sample (2005:Q1–2017:Q2). The results show a small negative response of GDP growth and inflation to contractionary policy in the first part of the sample, a larger but shorter-lived positive response after the introduction of inflation targeting, and a medium-sized negative response of longer duration in the last part of the sample. This suggests that the introduction of inflation targeting has led to a noticeable change in the effect of monetary policy on inflation, with a stronger response in the first decade of the regime. On the other hand, the results show the importance of the inflation-targeting regime in curbing inflation: before the introduction of inflation targeting, contractionary monetary policy had a small effect on inflation and over time the effect became stronger and longer lasting.
Dynamics of Australian economic activity and inflation
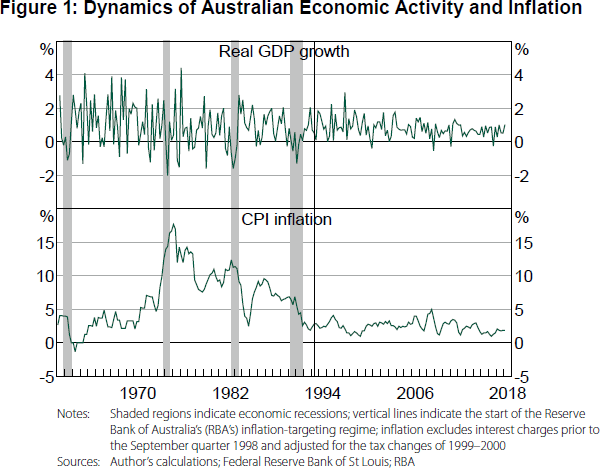
As can be observed in Figure 1, Australian real GDP growth and CPI inflation display substantial changes in their dynamics over time. Both the level and volatility of inflation have been decreasing, and GDP growth shows tamer oscillations. This has been the case since the mid 1990s, and it was more accentuated in the last decade. Features that stand out are that the stabilisation has both smooth and sudden changes in GDP growth and inflation. The challenge is how to account for these dynamics. Hartigan and Morley go beyond this question, aiming to investigate the potential effect of the inflation-targeting regime not only on inflation or GDP growth, but on a large panel of real and nominal economic variables using factor analysis.
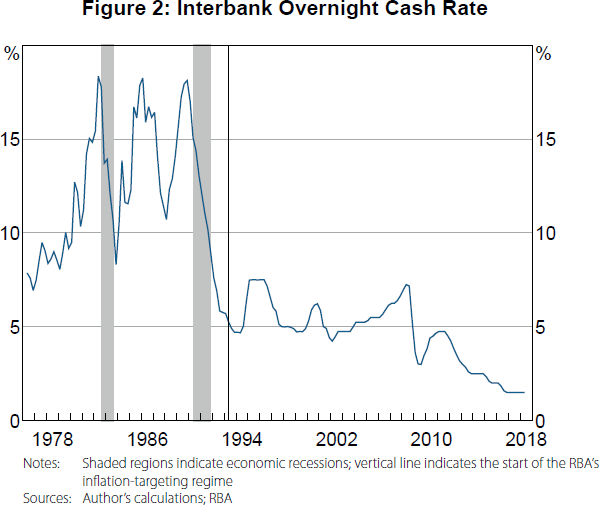
The paper shows that there is overwhelming evidence of a broad stabilisation in the real and nominal sectors of Australia, particularly since the inception of the inflation-targeting regime (Figure 2). There is evidence of multiple breaks in the factors and in the monetary transmission mechanism estimated through the proposed FAVAR. This has important consequences for the effect of monetary shocks on real economic activity and inflation, as shown in the paper and discussed below. The findings in the paper also raise several interesting research questions that can be explored further in the future.
Comments and suggestions
Summary
Hartigan and Morley implement a careful analysis, using a sequence of methods to provide insights about the economic and nominal stabilisation in Australia since the implementation of inflation targeting. The paper undertakes an extensive and meticulous analysis of structural breaks in both principal components and FAVAR methods and obtains interesting and thoughtful insights regarding changes in volatility and changes in the transmission mechanism of monetary policy.
I find the paper interesting and well executed with important new findings. Below, I give some comments and suggestions regarding the empirical application and modelling of the transmission of monetary shocks, which I think can improve the analysis in this and future papers.
I discuss the data transformation, the relationship between the real factor and production, and the possible existence of outliers and pulse (temporary) breaks that can bias the structural break tests. Additionally, throughout the sections in the paper, there seem to be multiple breaks in the real and nominal sectors. The evidence points to increased stabilisation more so than breaks in the level. I suggest recursive tests that have more power for multiple breaks, which would reduce the uncertainty regarding the location of the breakpoints. Further, I suggest that the tests for breaks in level and variance should be undertaken separately, as it could be the case that the breaks in these moments took place at different dates. A more extensive sub-sample analysis should be implemented based on the results of these tests.
Overall, the results seem to indicate that the decrease in volatility is not a one-time event, but it is a continuous process, with increased stabilisation over time and very minor oscillations in the last decade. It could be the case that the changes are recurrent or that the changes have taken place gradually. The paper implements an extensive analysis assuming that inflation targeting engendered structural breaks in the economy. Instead of studying the effect of exogenous breakpoints through sub-sample analysis, the paper could integrate potential breaks into the FAVAR model. For example, the FAVAR could be estimated with Markov switching in the mean and variance, which would allow analysis of recurrent changes, or of permanent structural breaks. Another possibility is to estimate the FAVAR with Markov switching in the mean parameters and allow for stochastic volatility.
Finally, I discuss the interpretation of the results regarding changes in the impulse response functions, sacrifice ratio and Phillips curve, compared with changes in monetary policy in the United States.
Data transformation
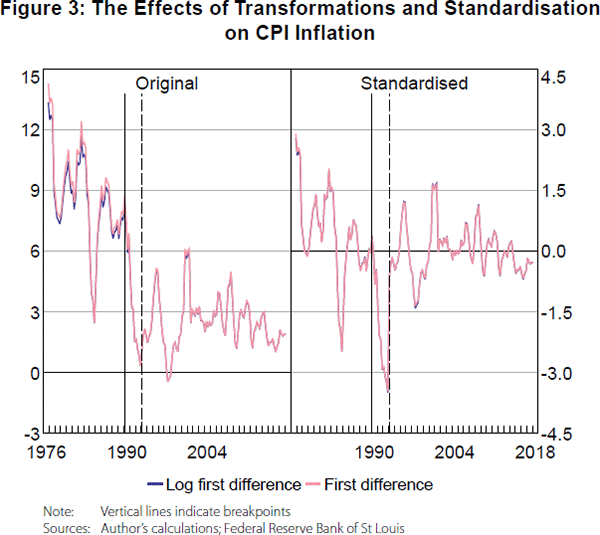
Comments. The series on price growth are a priori adjusted for a structural break in mean in 1993:Q1, corresponding to the beginning of inflation targeting. The goal is to make the series stationary without needing to take second differences. However, demeaning the series with an a priori breakpoint can engender problems in the subsequent analysis. First, as found throughout the paper, break locations are subject to uncertainty – the potential break in mean may have occurred before or after 1993. Second, even if there is a break in the series, it should remain in the data studied since it would be part of the evidence that there has been a structural change in inflation since the inception of inflation targeting. Demeaning and standardising the series around the break may reduce the evidence of a break in 1993 in the subsequent analysis. Finally, the Qu and Perron (2007) test indicates that there is a breakpoint in price growth in 1990:Q1 instead of 1993:Q1. This is consistent with the findings in the paper for the factor structure in Section 4.3.
Additionally, if there is a break in variance around the same time, in the early 1990s, the equalisation of the intensity of oscillations before and after inflation targeting with the data transformation might mask abrupt changes in volatility. It may also make smaller fluctuations in the latter part of the sample more important than warranted, compared with the 1970s and 1980s.
As an illustration, the left-hand panel of Figure 3 plots CPI in log growth rates and in differences, with the solid vertical line indicating a breakpoint in 1990:Q1 (as found in Qu and Perron's test) and the dashed line indicating a breakpoint in 1993:Q1 (as assumed in the paper).[1] The right-hand panel shows these series demeaned and standardised assuming a break in 1993:Q1 as in the paper. As seen, demeaning the series around 1993:Q1 masks the major change (break in mean and/or variance) in the dynamics of inflation between 1990 and 1993. This can show up in the factor analysis of the original data later on, which indicates higher macroeconomic stability since the beginning of inflation targeting.
Suggestions. One of the main methods used in the paper to examine the effect of inflation targeting on the Australian macroeconomy is analysis of potential structural breaks in the factor models. The whole analysis is performed on the premise that there are breaks in the structure of the economy. Thus, the a priori data transformation might be hindering a more precise detection of breaks in the factor analysis. My suggestion is that either the price growth series are used without any transformation, or that they be used in second differences if necessary to obtain stationarity instead of transformed by assuming a break in 1993:Q1.
Estimation and interpretation of factors
Comments. The results indicate that two factors capture most of the joint variation in the data. Interestingly, the variables with the highest correlations with the ‘real’ factor (Factor 1) are the surveys, which are expectation measures. Their correlation with the real factor is twice as large as with the next groups of variables (employment, expenditure and money and credit). On the other hand, the series measuring production have a low correlation with the real factor. Given the importance of the production sector in determining prices, a higher correlation between production and the real factor is desirable in the analysis of the channel of inflation targeting through the real sector.
Suggestions. There is a possibility that the real factor is out of phase with production – the real factor could be a leading indicator of the production sector (given that it is most correlated with survey series). This should be investigated. If this is the case, production variables should be added into the baseline FAVAR, as this would give a better assessment of the effect of monetary policy on and through the supply side of the economy.
Breaks in the factor structure
Comments. The paper tests for structural breaks in factor loadings using Han and Inoue's (2015) test. The LM test statistic is maximised in 1991:Q4 and the Wald test statistic in 1998:Q3. The paper finds that both tests are significant in 1993:Q1, around the time inflation targeting was implemented.
However, as seen in Figure 6 of the paper, the LM test is significant for an interval starting in 1990, roughly from 1990 to 2001 (with the exception of 1997), and the Wald test from 1993 to 2002. Thus, both tests are significant between 1993 and 2001 (not only in 1993). This implies that, at a minimum, there is uncertainty regarding the date of the structural break. This may also be an indication that perhaps there are multiple breaks, the changes are recurrent or have taken place gradually over time. Non-identification of further breaks does not imply that they are not present in the data as this could just reflect the power of the test.
Suggestions. The alternative hypothesis in the Han and Inoue (2015) test is that a fraction of or all factor loadings have a single break at a common date. This raises two issues. First, there might be more than one structural break and this would reduce the power of the test. Second, the break in different factor loadings might take place at different dates. If any of these possibilities is present in the factor structure for the Australian economy, the location and significance of the breaks might be uncertain. My suggestion is that the Han and Inoue (2015) test be implemented recursively and once a break is found, to restart the recursive test from then on to find other breaks.[2] Alternatively, the Yamamoto and Tanaka (2015) test can be used for multiple structural changes in factor loadings. The goal in both exercises is to find the breakpoint dates more precisely. However, these tests should be applied keeping in mind that there seems to be some pulse (temporary) breaks in the Australian economy. As seen in Figure 4 of the paper, the ‘nominal’ factor (Factor 2) has spikes in 1997 and 2000, and the real factor also in 2000, possibly related to the introduction of the goods and services tax.[3] Thus, the tests should also take these pulse breaks or outliers into account when recursively implemented.
In addition, given the uncertainty regarding the break dates, it might be the case that changes in the mean or volatility of the Australian macroeconomy occurred gradually over time, rather than at one or another point in time. The implementation of inflation targeting in 1993 may have affected expectations and uncertainty regarding the actions of the RBA more immediately, but the effects of monetary policy on the volatility of the economy may also have happened over time. For example, the volatility of inflation itself is smaller in the 2000s than in the 1990s. Modelling recurrent or gradual changes is further discussed below.
Decline in the volatility of common shocks
Comments. The paper finds that the volatility of common components reduced substantially over time. This is the case for the real and nominal variables, and also for the common component of CPI inflation. On the other hand, the idiosyncratic volatility for all sectors has not shown a reduction. In addition, the factor loadings display stabilisation coinciding with the implementation of inflation targeting.
Suggestions. First, the evidence is mostly from looking at the volatilities in Figure 7 rather than statistical tests. Tables with statistics of the volatilities across sub-samples should be provided, possibly for more sub-samples as determined by the several breaks found in the paper, for example, before 1990:Q1, before 1993:Q1, between 1990:Q1 and 2007:Q4, between 1993:Q2 and 2007:Q4, covering the global financial crisis and European debt crisis between 2008:Q1 and 2012:Q4, and from 2013:Q1 to the end of the sample.
Second, the evidence from the Han and Inoue (2015) test, recursive factor loadings and cross-correlation volatility indicate that the major change in the Australian economy since the inception of inflation targeting has been an increased stabilisation in both the real and nominal sectors. Increased stabilisation (in addition to a reduction in the inflation level) has important positive implications for welfare, for planning, for the structure of the economy, as well as for the transmission of monetary policy shocks. Specific tests for changes in volatility should be implemented. Further, the implications and linkages of the lower volatility and effect of monetary policy in the real and nominal sectors could be more thoroughly explored in the paper, as discussed below.
Transmission of monetary policy shocks – FAVAR model and break tests
Comments. The proposed FAVAR is estimated for the full sample and for three sub-samples. The model yields sensible and insightful results. The break test by Qu and Perron (2007) is appropriate as it tests for breaks in the mean and/or variance. The test is applied recursively, allowing for multiple breaks. However, there are some problems in the test and sub-sample analysis. First, the test assumes that breaks in mean and volatility happen at the same time. The paper does not consider the possibility that there could be breaks in the regression coefficients and in the variance at different times. Breaks in volatility can contaminate the results of breaks in the persistent parameters and it can affect the impulse response functions.
Suggestions. Andrews and Ploberger's (1994) test can be recursively applied separately for breaks in mean and for breaks in variance. This will allow direct evaluation of changes in volatility over time and since the implementation of inflation targeting. It will also allow analysis of changes in impulse response functions over time. Since the breaks were a rough guideline to choose the sub-samples used in the paper, and the impulse response functions are different across periods, the break dates are important and could be re-examined to study potential changes in the transmission of monetary policy shocks.[4]
Alternatively, instead of studying the impact of exogenous breakpoints through sub-sample analysis, the paper could integrate potential breaks into the FAVAR model. For example, the FAVAR could be estimated with Markov switching in the mean and variance. This model approach would allow analysis of recurrent changes or of permanent structural breaks by modelling the transition probability with an absorbing state. Another option is to estimate the FAVAR with Markov switching in the mean parameters and allow for stochastic volatility. One of the main findings of the paper is increased stabilisation over time. Thus, allowing for a FAVAR with some sort of dynamics in the variance is important to capture this feature.
In all cases, as in the previous analysis, the model should be estimated taking into account potential pulse breaks in 1997 and 2000 as discussed earlier.
Changes in impulse response functions over time and the price puzzle
Comments. In order to illustrate the importance of changes in the monetary transmission of shocks over time, Chauvet and Tierney (2018) estimate a structural vector autoregression (SVAR) of US real-time GDP growth, inflation, unemployment and interest rates. The model is recursively estimated over increasing samples, yielding time series of the coefficients, variances and impulse response functions resulting from each recursive estimation. These are shown in Figure 4, which plots the impulse response functions of output and inflation to an unexpected increase in the federal funds rate in 1975:Q1, 1980:Q4 to 1981:Q3, 1996:Q1 and 2006:Q4. These dates are selected to reflect different economic conditions and to represent the governance of Burns, Volcker, Greenspan and Bernanke. The paper finds a reduction in the effect of monetary policy shocks, especially with respect to the response of inflation.
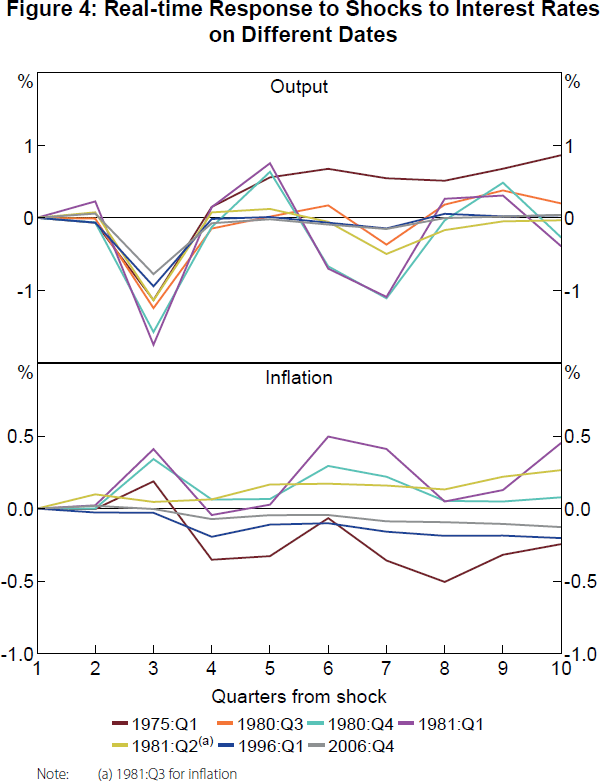
Monetary policy shocks have a strong and lasting negative effect on output during the Volcker period, especially between 1980:Q3 and 1981:Q3, and have the weakest effect in the later dates of 1996:Q1 and in 2006:Q4. The response of inflation to monetary policy shocks shows an even greater time variation. The largest negative response occurs in 1975:Q1, in the Burns period, followed by milder, but still negative, effects in the Greenspan and the Bernanke periods (1996:Q1 and 2006:Q4, respectively). On the other hand, inflation shows a positive response in the Volcker period between 1980:Q4 and 1981:Q3, even though the SVAR considered includes commodity price inflation to minimise the price puzzle. Notice that the price puzzle does not appear in other periods.
Suggestions. Hartigan and Morley find the price puzzle for the nominal factor and for CPI inflation for the full sample, and for the period between 1993:Q2 and 2004:Q4, but not for the other sub-samples. This might be a consequence of the disinflation that took place between 1993:Q2 and 2004:Q4, similar to the one observed in the United States in the early 1980s. It could also be due to the existence of breaks (non-stationarities) around the period between 1990 and 1993, which can lead to very different impulse responses quarter by quarter, as illustrated in Chauvet and Tierney (2018). The paper could further explore this possibility by separating and estimating the model using several sub-samples around this period. It could also add commodity price variables to the FAVAR, which is known to reduce the price puzzle. Finally, adding the production variables may reduce the price puzzle as well, since the real factor is mostly associated with surveys of expected output rather than with production per se, as discussed earlier.
Sacrifice ratio and the Phillips curve
Comments. The paper examines the sacrifice ratio for Australia using the accumulated response of real GDP relative to the response of CPI inflation. The authors find that it dropped with the introduction of inflation targeting, but it has increased since the mid 2000s. The paper relates this to a possible flattening of the Phillips curve. However, the sacrifice ratio could have increased because the inflation level is low enough during this more recent period that changes in interest rates do not change inflation as much, since it is not warranted. This can be seen in the impulse response function in the later part of the sample – inflation does not fall as much as a response to a shock in monetary policy compared with the earlier phase of the inflation-targeting period. This might indicate that the sacrifice ratio is higher not because of the response of output compared with earlier periods, but because inflation is responding less than output since the mid 2000s – which is also found in the United States. This is an expected result in an environment with low inflation, as found also in Chauvet and Tierney (2018) for the United States.
Suggestions. If the paper wants to further study the Phillips curve or the RBA reaction function, it can use the results from the FAVAR to estimate these equations as, for example, in Cogley and Sargent (2005), and draw more definite conclusions regarding changes in the Phillips curve. More interestingly, the paper should further explore the implications of (lower) levels and volatility of inflation on inflation's response to monetary policy shocks.
Footnotes
Marcelle Chauvet is a professor of economics at the University of California, Riverside and a Director of the International Association for Applied Econometrics [*]
Note that although CPI growth is corrected for the tax changes of 1999–2000 and the interest charges prior to 1998, the other price series used in the paper are not. Thus, the effects of the goods and services tax may still show in the factors as discussed in the next section of this discussion. [1]
Note that although the power of the Han and Inoue (2015) test increases for longer samples, it also decreases in the presence of multiple breaks. [2]
GDP growth also displays a spike in 1997, as observed in Figure 1. [3]
The paper finds breaks in 1990:Q1 and 2010:Q2 for the real factor equation, a break in 2011:Q1 for the nominal factor equation, and breaks in 1990:Q3 and 2011:Q1 for the OCR equation. The sub-samples chosen are 1976:Q4–1993:Q1, 1993:Q2–2004:Q4 and 2005:Q1–2017:Q2. Regarding the sub-samples used, the paper should part them according to the breaks found. Here, again, I would suggest before 1990:Q1, before 1993:Q1, 1990:Q1–2007:Q4, 1993:Q2–2007:Q4, 2008:Q1–2012:Q4 and 2013:Q1–2017:Q2. [4]
References
Andrews DWK and W Ploberger (1994), ‘Optimal Tests When a Nuisance Parameter is Present Only under the Alternative’, Econometrica, 62(6), pp 1383–1414.
Chauvet M and HLR Tierney (2018), ‘Real Time Changes in Monetary Policy’, Unpublished manuscript, University of California, Riverside.
Cogley T and TJ Sargent (2005), ‘Drifts and Volatilities: Monetary Policies and Outcomes in the Post WWII US’, Review of Economic Dynamics, 8(2), pp 262–302.
Han X and A Inoue (2015), ‘Tests For Parameter Instability in Dynamic Factor Models’, Econometric Theory, 31(5), pp 1117–1152.
Qu Z and P Perron (2007), ‘Estimating and Testing Structural Changes in Multivariate Regressions’, Econometrica, 75(2), pp 459–502.
Yamamoto Y and S Tanaka (2015), ‘Testing for Factor Loading Structural Change under Common Breaks’, Journal of Econometrics, 189(1), pp 187–206.
2. General Discussion
Much of the discussion was focused on identification and causality, with participants noting that macroeconomic volatility had fallen globally over the sample period. A number of participants suggested that causality from the introduction of inflation targeting to lower macroeconomic volatility in Australia was hard to determine because other structural factors may have had significant effects around the same time.
One participant noted that empirical work for small open economies such as Australia should be easier than similar analysis for the United States. This is because variables such as global commodity prices, global gross domestic product and global interest rates can be treated as exogenous when examining small economies. Another participant agreed and stated this would help identify whether the low global inflation had caused lower inflation in Australia.
Participants also discussed alternative reasons for why macroeconomic volatility may have fallen in Australia in the early 1990s. Alternatives raised included the Great Moderation, tariff reductions, structural changes in the regulation of product markets, the increased use of information technology and the deregulation of the labour market. Another reason raised was the decentralisation of wage determination, which occurred through the late 1980s and early 1990s. This reduced the propagation of commodity price shocks to other sectors that likely contributed to the fall in macroeconomic volatility. One participant suggested that relaxing the assumption of a single break date could reveal something about the timing. All of these factors, as well as inflation targeting, occurred over time and this may be why the break dates in Luke Hartigan and James Morley's analysis were inconclusive.
However, participants also referred to the sharp decline in common volatility and in the volatility of the main categories of ‘real’ and ‘nominal’ variables around the introduction of inflation targeting. While there was uncertainty in the confidence intervals of the break tests, the abrupt change in volatility in 1993 suggested that the introduction of inflation targeting did contribute to the fall in macroeconomic volatility.
Another major area of discussion was focused more on the implications of inflation targeting for identification. One participant noted inflation targeting is about more than just establishing a nominal anchor – it's also about moving towards a more transparent and systematic policy framework. In an ideal world, central banks should be moving interest rates endogenously to stabilise the economy. Participants agreed that this would not provide monetary policy shocks for identifying the effect of monetary policy on macroeconomic variables. It seems that the last decade has had less variation in monetary policy than previous years, which makes identification harder.
One participant stated that solving the inference problem is getting harder because all movements are being dominated by idiosyncratic volatility. Central banks are now looking at a wider group of variables, which makes communication trickier because the economic narratives must be more nuanced. The participant noted that, the more successful inflation targeting is, the more the central bank needs to rely on communication. Another participant agreed and said that, the more relative noise there is, the more the central bank needs to communicate about why it is looking through it. However, they also noted that inflation targeting has been successful because it targeted a single variable and targeting a factor would not be beneficial as it would be much more difficult to communicate to the public.