RBA Annual Conference – 2013 Bank Funding and Financial Stability Prasanna Gai, Andrew G Haldane, Sujit Kapadia and Benjamin Nelson[*]
1. Introduction
The crisis of 2007–2008 was a crisis of collateral. Since then, financial market participants – particularly in the euro area and the United States – have shown an increased appetite for secured lending. In short-term bank funding markets, there has been a pronounced shift towards repurchase arrangements. And covered bonds have gained in popularity in long-term funding markets. The cyclical flight to safety, driven by market forces, has been reinforced by regulatory developments. These include reforms to over-the-counter derivative markets that emphasise more stringent collateralisation, preferential regulatory treatment of covered bonds, and the prospect of statutory ‘bail-in’ tools for financial regulators.
The financial stability implications of increased collateralisation of financial transactions and rising bank asset encumbrance levels remain poorly understood. From a microprudential perspective, secured funding – especially when long term – would appear desirable since it increases funding diversity and seemingly reduces funding liquidity risk particularly during periods of market stress.
From a macroprudential perspective, however, there are grounds to be less sanguine. High encumbrance levels, particularly if opaque, can reduce the assets available to unsecured creditors, leading to higher costs of borrowing from such funding sources and heightening incentives to finance on secured terms. And, as assets are increasingly encumbered, the financial system as a whole may become riskier as it is more susceptible to procyclical swings in the underlying value of the (increasingly common) collateral assets (Haldane 2012). During economic downturns, falling collateral values and higher haircuts require more assets to be pledged to raise a given level of funding. This, in turn, may necessitate reduced balance sheet leverage via asset sales, limit new banking activities and potentially heighten investor concern about bank viability.
In this paper, we present a simple analytical model of bank funding to shed some light on the relationship between liquidity risk, solvency risk, and collateral values. We apply ideas from the literature on global games (Morris and Shin 2003, 2010) to provide an accounting framework to decompose balance sheet risk and to solve for the rollover games being played by unsecured and secured creditors. In the model, total bank risk is decomposed into insolvency risk and illiquidity risk and the two are jointly determined as a function of the underlying parameters of the model. Although cast as a partial equilibrium treatment of a single bank, our analysis is nevertheless suggestive. The parameters that we treat as exogenous would become endogenous in a model of a banking system and reflect broader market and macroeconomic conditions. As such, they become natural channels for the transmission of financial stability problems.
Our analysis reveals the importance of the maturity of secured debt through the trade-offs faced by secured creditors. In the model, secured creditors have recourse to ring-fenced collateral in the form of a risky, illiquid asset and earn lower returns relative to unsecured creditors. A bank improves its profitability and thus solvency position by relying on long-term secured funding. But the impact on liquidity risk is ambiguous – while increased long-term stable funding improves ex ante liquidity risk by replacing fickle short-term debt, it also reduces the amount of unencumbered collateral that can be liquidated to service early withdrawals. If, instead, the bank seeks out short-term secured funding, interim liquidity risk and asset encumbrance become intimately intertwined. We show how factors that worsen the interim liquidity position of the bank lead secured creditors to endogenously demand more collateral which, in turn, compounds the likelihood of a run by unsecured creditors.
We are also able to obtain some simple comparative static results that shed light on the consequences of greater collateralisation of bank balance sheets for the procyclicality of the financial system. In our model, the liquidation or market value of collateral can be viewed as reflecting the state of the macroeconomy and the sensitivity to liquidity risk varies with collateral values. As banks strive to fund their operations via secured funding, their exposure to such liquidity risk can become greater than in the case where funding is by unsecured short-term debt alone. In particular, if too few assets are pledged as collateral, exposure to the risk of falls in the market value of collateral is heightened, even when secured funding is long term in nature. And when secured funding is short term, the endogeneity of asset encumbrance and the possibility of a dash for collateral exacerbate the sensitivity of liquidity risk to collateral values. In this context, we show that the imposition of minimum regulatory haircuts may reduce the sensitivity of a bank's liquidity position to variation in collateral values and thus the procyclical fluctuations generated by secured debt.
Notwithstanding considerable policy interest (e.g. CGFS 2013), the relationship between financial stability and asset encumbrance has received scant attention in the academic literature. Roland and Sowerbutts (2013) consider the factors driving asset encumbrance, such as Knightian uncertainty and the removal of implicit deposit guarantees. But their model does not consider the implications for bank liquidity risk or the impact of increased collateralisation for the procyclicality of the system. Anand, Chapman and Gai (2012) focus on covered bonds, and also use a global games approach to model the risk of a run by unsecured creditors. Following a shock, the balance sheet of the bank has to be adjusted to ensure the quality of ring-fenced assets backing the covered bond, and the critical threshold for a run depends on the extent of asset encumbrance and the liquidity of secured lending markets. Rinaldi (2011), like the present paper, also highlights the possibility of runs by secured creditors. But her focus is on the role played by ambiguity and ambiguity aversion in generating credit market freezes. Finally, a line of literature considers the amplification role of haircut shocks in generating procyclicality (e.g. Brunnermeier and Pedersen 2009; Adrian and Shin 2010; Geanakoplos 2010; Gorton and Metrick 2010; Gai, Haldane and Kapadia 2011) but typically does not consider this in light of the interplay between secured and unsecured debt or in the context of the move towards greater asset encumbrance.
The paper proceeds as follows. Section 2 presents some stylised facts on bank funding and asset encumbrance patterns, documenting some regulatory changes that are contributing towards increased collateralised borrowing. Section 3 outlines the model, and sets out how the liquidity risk of a bank changes with the composition of bank funding. We present the case of a bank financed solely with unsecured debt as a benchmark, and contrast the bank's liquidity risk in this case with the liquidity risk that obtains under long-term and short-term secured funding. Section 4 concludes with some policy implications in the context of the ongoing debate on regulatory reform.
2. Stylised Facts
Figures 1 and 2 show the extent to which wholesale bank funding in Europe has become increasingly collateralised. Prior to the crisis, collateralised debt and asset encumbrance were most prominent in countries with a long tradition in covered bonds (e.g. Germany and Spain). But by 2011, asset encumbrance had risen markedly in countries with strained finances, such as Ireland, Greece and Italy. Figure 2 illustrates the clear recent increasing trend in the encumbrance ratios, after a prolonged plateau, of Swedish banks. The shift to collateralisation by UK financial institutions has also been marked – the proportion of system assets encumbered rose to around 5 per cent by 2011, although alternative approaches to estimating encumbrance ratios can give figures of up to 20 per cent (Bank of England 2012).
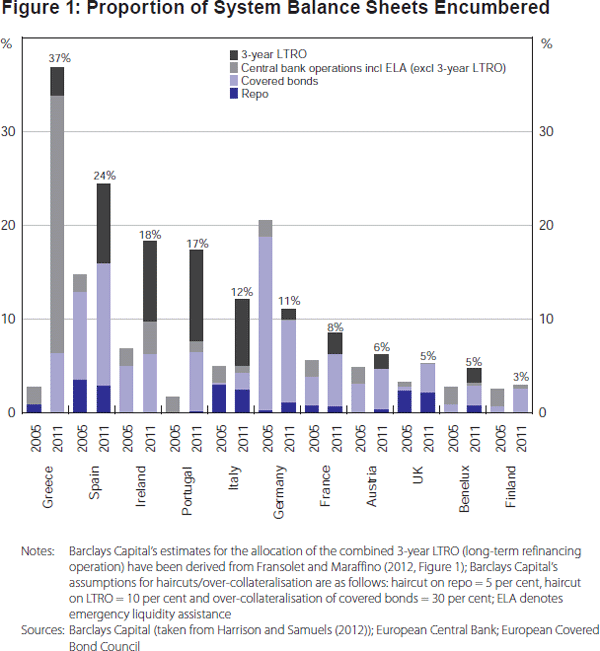
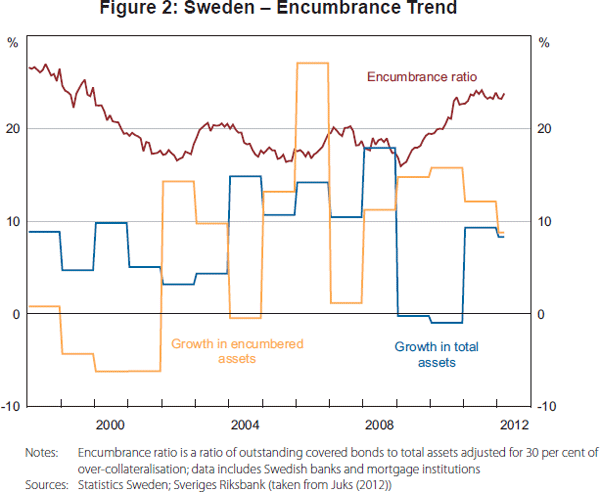
Table 1 shows how the reliance on long-term secured lending, in the form of covered bonds, has increased in a number of countries. Meanwhile, US banks remain significantly reliant on short-term secured funding – for example, net repos and financial market open paper stood at around 20 per cent of total retail deposits in 2011 (Figure 3). At the same time, it should be noted that one counterpart to these overall trends has been the shrinkage of private-sector asset-backed securities markets.
| Country | 2003 | 2005 | 2007 | 2009 | 2010 | 2011 | 2012 |
|---|---|---|---|---|---|---|---|
| Canada | 2,000 | 7,525 | 18,003 | 38,610 | 49,121 | ||
| Denmark | 204,695 | 246,411 | 244,696 | 319,434 | 332,505 | 345,529 | 359,560 |
| France | 21,079 | 32,133 | 63,555 | 134,757 | 156,239 | 198,395 | 208,297 |
| Germany | 256,027 | 237,547 | 206,489 | 255,100 | 219,947 | 223,676 | 215,999 |
| Italy | 14,000 | 26,925 | 50,768 | 116,405 | |||
| Netherlands | 2,000 | 15,973 | 29,057 | 41,273 | 54,115 | 61,515 | |
| Spain | 57,111 | 150,213 | 266,959 | 336,750 | 343,401 | 369,208 | 406,736 |
| Sweden | 92,254 | 133,903 | 188,750 | 208,894 | 220,374 | ||
| United Kingdom | 5,000 | 28,384 | 84,874 | 200,466 | 203,215 | 185,052 | 185,243 |
|
Source: European Covered Bond Council (adapted from CGFS (2013, p 7)) |
|||||||
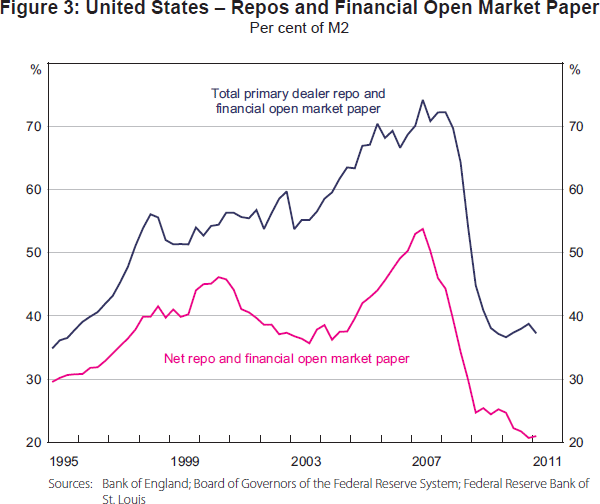
Figure 3 also illustrates how collateralised debt and, in particular, the haircuts associated with it play a key role in procyclical behaviour. Prior to the crisis, haircuts were extremely compressed and marginal leverage was relatively high. But as haircuts rose sharply during the crisis, the subsequent decline in marginal leverage reinforced the downturn in the credit cycle. Although data on haircuts are sparse, there is reason to believe that they exhibit procyclicality. Table 2 presents the best available information on the evolution of haircuts on collateralised lending during the global financial crisis – haircuts on some securities financing transactions rose by up to 90 percentage points between 2007 and 2009.[1]
| June 2007 | June 2009 | ||||||
|---|---|---|---|---|---|---|---|
| Prime(a) | Non-prime(b) | Unrated(c) | Prime(a) | Non-prime(b) | Unrated(c) | ||
| G7 government bonds | |||||||
| Short-term | 0 | 0 | 0.5 | 0.5 | 1 | 2 | |
| Medium-term | 0 | 0 | 0.5 | 1 | 2 | 3 | |
| US agencies | |||||||
| Short-term | 1 | 2 | 3 | 1 | 2 | 3 | |
| Medium-term | 1 | 2 | 3 | 2 | 5 | 7 | |
| Pfandbrief | 0 | 0 | 1 | 1 | 2 | 8 | |
| Prime mortgage-backed securities | |||||||
| AAA-rated | 4 | 6 | 10 | 10 | 20 | 30–100 | |
| AA- and A-rated | 8 | 12 | 25 | 100 | 100 | 100 | |
| Asset-backed securities | 10 | 20 | 20 | 25 | 50 | 100 | |
| Structured products (AAA) | 10 | 15 | 20 | 100 | 100 | 100 | |
| Investment-grade bonds | |||||||
| AAA- and AA-rated | 1 | 2 | 5 | 8 | 12 | 15 | |
| A− and BBB-rated | 4 | 7 | 10 | 10 | 15 | 20 | |
| High-yield bonds | 8 | 12 | 20 | 15 | 20 | 40 | |
| Equity | |||||||
| G7 economies | 10 | 12 | 20 | 15 | 20 | 25 | |
| Emerging economies | 15 | 20 | 35 | 20 | 25 | 40 | |
|
Notes: Data were gathered by a CGFS Study Group during bilateral interviews
with market participants; a 100 per cent haircut implies that the relevant
market was effectively closed Source: CGFS (2010) |
|||||||
A number of recent regulatory changes suggest that the trend towards secured wholesale funding seems set to continue (see also Bank of England (2012)). First, the G20 has mandated that standardised OTC derivative contracts be centrally cleared. While not directly increasing secured funding, the increased posting of collateral that this entails will increase asset encumbrance and expose financial firms to fluctuations in collateral values.
Second, covered bonds have preferential regulatory treatment both because they are included as Level 2 assets under the new Liquidity Coverage Ratio of Basel III, and because reforms for insurers under Solvency II will require insurance companies to have less capital against exposure to covered bonds than against unsecured debt with the same issuer. These regulatory rules might serve as an incentive to banks to increase their use of covered bonds.
Third, depositor preference can reduce recovery values for unsecured creditors and, so, make secured funding more attractive to issue. Law in Australia, as well as in the United States and Switzerland, already establishes depositor preference. The European Council has recently agreed to introduce tiered depositor preference into the bank resolution framework. And legislation is being introduced in the United Kingdom to give insured depositors preference above unsecured creditors in a debt workout.
Finally, new crisis resolution frameworks are likely to include a statutory ‘bail-in’ tool that would allow resolution authorities to write down unsecured debt or convert it to equity when a distressed bank enters resolution. Covered bonds and other forms of secured debt are excluded from writedowns under some frameworks and, while not changing the position of unsecured debtholders in the creditor hierarchy, bail-in makes it more likely that unsecured creditors will suffer losses should a large, complex financial firm fail. At the same time, it should be noted that likely future requirements on systemically important financial institutions to maintain an adequate amount of gone-concern loss-absorbing capacity in resolution (FSB 2013a) should counter some of these tendencies to move away from unsecured debt.
3. Analytical Framework
Our framework is inspired by Morris and Shin (2010) and describes how the insolvency and illiquidity risks of a financial institution are influenced by the way it funds its business activities. In particular, we highlight how a shift from unsecured to secured funding affects both the level of bank risk and its sensitivity to fluctuations in collateral values. We also distinguish between short-term and long-term secured funding and model ‘dashes for collateral’ by secured creditors.
3.1 Unsecured funding
The bank's balance sheet takes the simple form in Morris and Shin (2010). On the asset side, the bank holds two assets: cash, M, and Y units of a risky asset, such as loans or risky securities. The funding for these assets comes from short-term unsecured debt, D, and equity, E. Accordingly,

There are three dates, τ = 0, 1, 2. Each unit of the risky asset pays a gross amount θ2 in date 2, so the bank is solvent at the final date if ex post equity is positive, that is

where D2 is the date-2 face value of unsecured debt. Equivalently, we can define a critical return or ‘solvency point’ for the bank:

We assume that if the bank is insolvent at date 2, i.e. θ2< θ** then the bank goes into liquidation and the creditors do not receive any pay-off.
At the interim date, unsecured creditors must decide whether to roll over their lending. The bank can liquidate cash and its holdings of risky assets to service withdrawals by its creditors – cash is liquidated at par, but risky assets fetch an amount ψ ∈ [0, 1] when liquidated. The interim resources available to the bank are therefore:

If the proportion of creditors that choose not to roll over their loans is λ ∈ [0, 1], the bank fails from a run at the interim date if the debt withdrawn exceeds interim resources. That is:

When Equation (5) holds with equality, we can define the bank's ‘liquidity ratio’, as:

As λ* rises, a run is less likely to result in failure. In keeping with the global games literature, we suppose that unsecured creditors believe that the proportion of creditors that do not roll over their loans is uniformly distributed over the interval [0, 1]. If the bank fails because of a run, creditors that do not withdraw receive nothing (zero recovery). Accordingly, each creditor believes that the probability of a run being successful is 1 − λ*.[2]
We also can relate the solvency point and liquidity ratio to key balance sheet ratios using Equation (1). In particular, dividing through by Y,

where
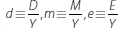 reflecting the
bank's short-term debt ratio, the cash-asset ratio and the risk-weighted
equity ratio (assuming a zero risk-weight on cash and a weight of unity on
risky assets). The solvency point can thus be expressed as
reflecting the
bank's short-term debt ratio, the cash-asset ratio and the risk-weighted
equity ratio (assuming a zero risk-weight on cash and a weight of unity on
risky assets). The solvency point can thus be expressed as

where r ≡ D2/D is the return on unsecured debt. As θ** rises, insolvency becomes more likely. So a higher cash-asset ratio, a lower equity ratio, or a higher interest rate all make insolvency more likely.
In a similar vein, the liquidity ratio can be expressed as:

A higher equity ratio (and hence less debt financing) makes the bank less likely to suffer from interim liquidity shortages. Note also that the higher the liquidation value of the risky asset, the less likely is a bank run:

What is the risk that the bank fails when it only has recourse to unsecured debt? If the return at date 2 is θ2, let θ1 and θ0 denote the date-2 returns expected at dates 1 and 0, respectively. And let

where ετ ~ øτ, øτ denotes the densities (with associated cumulative density functions, Φτ, assumed to be normal) of the zero mean shocks, ετ, that are independent across dates. Thus, at the interim period, with date-2 returns expected to be θ1, solvency risk is:

Since the date-1 expectation of returns is a random variable from the perspective of date 0, the insolvency risk at date 0 is:

Next we define illiquidity risk as follows. At date 1, suppose creditors have an outside option r*. If the probability of a run being unsuccessful is λ*, and the probability of avoiding insolvency is 1 − N1(θ1), expected date-2 returns at date 1 must be such that the creditor is indifferent between rolling over and withdrawing. Thus the critical threshold for date-1 expectations about date-2 returns below which a run occurs, θ*, must satisfy:

And so interim illiquidity risk is

or

Note that when σ2 > 0, the insolvency and illiquidity points differ in general. In particular:
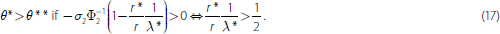
When this is the case, the bank is insolvent for θ2 < θ**, solvent but illiquid for θ2 ∈ [θ**, θ*], and solvent and liquid for θ* < θ2.
3.2 Secured funding
We now suppose that the bank can also fund itself with long-term secured debt, S. The bank's balance sheet now becomes:

Solvency at the final date now requires that

where S2 is the face value of secured debt in the final period. The solvency point is now:

To raise secured debt, the bank pledges a fraction, α ∈ [0, 1], of risky assets to its secured creditors, ‘ring-fencing’ this fraction from the rest of the bank's balance sheet. We initially treat α as fixed, returning later to endogenise it. But the extent of the ring-fence can also be thought of as having been determined at date 0, effectively making the debt long term in nature.
A rise in α reduces the amount of available collateral that can be liquidated at the interim date to service unsecured withdrawals. The bank fails from a run if

since (1 − α)Y risky assets are available for liquidation in the interim period. The liquidity ratio thus becomes:

As before, we can express the solvency point in terms of the bank's balance sheet ratios, namely

where s ≡ S/Y is the secured debt ratio, and rS = S2/S is the return on secured debt. Whenever rS < r, i.e. secured debt is relatively cheap, a rise in the secured debt ratio improves solvency by substituting cheap secured funding for more expensive unsecured funding.[3] The liquidity ratio in the presence of secured debt is now:

The fact that secured debt requires assets to be pledged causes the bank's liquidity position to deteriorate (λ* is decreasing in α); but since secured debt is long term, a higher secured debt ratio, s, helps to improve the bank's liquidity position by reducing reliance on ‘flighty’ funding (λ* is increasing in s). Our model thus suggests that while long-term secured funding improves bank solvency if secured debt is relatively cheap, the effects on liquidity risk are more ambiguous. While the amount of collateral that is available to service interim withdrawals by unsecured creditors is lowered, the bank's ex ante vulnerability to such runs is reduced, since flighty funds are replaced with stable funding.
Note further that:

Compare this to Equation (10). The sensitivity of the liquidity ratio to risky asset
values increases in the presence of long-term secured debt only when
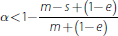 .
.
The bank becomes more exposed to interim liquidity risk in the presence of long-term
secured debt than in the case where it funds using short-term unsecured debt
alone and the fraction of pledged assets is small. To see this, consider the
case α = 1. In this instance, all risky assets are ring-fenced and
pledged to secured creditors. So their collateral value is irrelevant from
the point of view of unsecured creditors. Liquidity risk rises in a levels
sense since
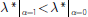 . But because
risky assets can never be liquidated to meet withdrawals by unsecured creditors,
their liquidity value does not matter for liquidity risk − λ*
becomes independent of ψ and a potential source of cyclicality
is removed.
. But because
risky assets can never be liquidated to meet withdrawals by unsecured creditors,
their liquidity value does not matter for liquidity risk − λ*
becomes independent of ψ and a potential source of cyclicality
is removed.
3.3 Endogenous asset encumbrance
We now allow secured debt to have a more short-term flavour. At the interim date, the probability of an unsecured bank run being successful is 1 − λ* Short-term secured creditors are able to ‘dash for collateral’ and demand that collateral be posted at the interim date in order to cover themselves against the possibility that the bank may suffer a run and enter resolution. As such, they demand collateral α Y, which can be used to obtain cash ψαY. In the event of a run, expected losses are covered by the liquidation value of pledged assets, that is ψαY = (1 − λ*)S. It follows, therefore, that the fraction of pledged assets needed to support an ex ante debt ratio of s for a given resale value of collateral ψ is:

In describing the bank's interim liquidity risk, there are now two equations, Equations (24) and (26), in two unknowns λ* and α. From Equation (24), a reduction in ψ reduces λ*, making a run more likely; and from Equation (26), a reduction in ψ increases α, which further reduces λ*. Secured debtholders thus endogenously demand that more collateral is posted as interim liquidity declines, compounding the effects of declining asset liquidity on the probability of a bank run by unsecured creditors.
Solving Equations (24) and (26) yields

and

which imply that

Comparing Equations (29) and (25), we see that when creditors can scramble for collateral, the probability of a run becoming successful becomes much more sensitive to collateral values than would otherwise be the case. And, compared to the model with unsecured creditors only, Equation (10), the bank's liquidity risk is much more sensitive to collateral values. This is because, with secured debt, the interim resources available to unsecured creditors vary with pledged collateral, and the pledged collateral – in turn – varies with its resale value. Our framework thus highlights the possibility that short-term secured debt can exacerbate the sensitivity of liquidity risk to collateral values.
Finally, the analysis can be extended to allow for the possibility that secured creditors
may also seek to guard themselves against solvency risk. Recall that the probability
of the bank being insolvent, when viewed from a date-1 perspective, is
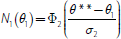 . So if collateral
is demanded in the interim period to cover against both the possibility of
a run and insolvency,
. So if collateral
is demanded in the interim period to cover against both the possibility of
a run and insolvency,
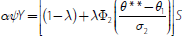 so that:
so that:
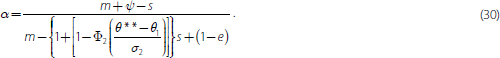
There is now a channel through which solvency risk influences the probability of a run. When the solvency point (θ**) rises, secured creditors demand more collateral. And there is less cash available at the interim date, worsening the bank's liquidity position (λ* falls). The illiquidity threshold in this case is given by:
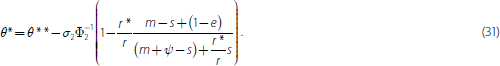
4. Some Policy Implications
At present, while improving, gaps remain in our knowledge about the true level of asset encumbrance and the risks it poses for banks (Enhanced Disclosure Task Force 2013). There is also a paucity of data surrounding the haircuts applied to collateralised financial transactions. Improved disclosure on asset encumbrance could help improve investors' ability to price debt correctly and enable banks to maintain an appropriate balance between secured and unsecured debt. This underpins the recommendation of the Enhanced Disclosure Task Force that banks should summarise asset encumbrance information in their annual accounts. But in thinking about the form of disclosure, it should be noted that market discipline can very easily give way to excessive reaction by investors in the face of unfavourable news, particularly under conditions of market stress. Our model suggests how unsecured creditors may become more jittery when confronted with the prospect of falling collateral values and expectations that the bank's asset encumbrance might increase.
Our analysis also suggests a role for structural and cyclical macroprudential policy. In terms of structural initiatives, macroprudential regulation that seeks to restrict the share of assets encumbered and limit the types of secured funding could mitigate financial stability risks. Caps on covered bond issuance already exist in some jurisdictions (e.g. Australia, New Zealand and Canada) and range from 4 to 10 per cent of depositor assets. But in other countries, there is uncertainty surrounding asset encumbrance policy, with regulators exercising discretion in setting thresholds. Our results highlight the risks of excessive asset encumbrance, especially if banks do not have sufficient gone-concern loss-absorbing capacity.
Adjusting haircuts on secured financing either by imposing minimum requirements, or by controlling them to mitigate procyclical tendencies, could also promote the resilience of financial institutions. Time-varying liquidity requirements and time-varying risk weights on particular secured financing transactions could also serve a similar purpose. For example, by acting against the endogenous collateral requirements of short-term secured debt holders, a time-varying haircut policy could temper the sensitivity of liquidity risk to collateral values. But such a policy could face trade-offs.
To see the effect of minimum regulatory haircuts, and to capture the spirit of this
form of regulation, suppose a regulator intervenes in the setting of collateral
requirements for secured transactions. In particular, let the regulator mandate
that haircuts on secured debt be set to h so as to guard against particularly severe outturns for asset prices,
ψ. Denote the ‘stressed’ value of asset prices for
the purpose of setting regulatory haircuts to be
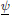 <ψ,
such that secured transactions must occur with levels of collateralisation
governed
by:[4]
<ψ,
such that secured transactions must occur with levels of collateralisation
governed
by:[4]

Analogously to Equation (26), the level of encumbrance is then:

To see how this relates to the ‘haircut’ h in the secured transaction, define

that is the haircut is akin to the inverse of leverage permitted by the regulator in secured funding transactions. Using the modified value of α in Equation (33), this gives the haircut as:

When the regulator allows secured transactions to occur at market prices, min(
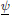 ,ψ)=ψ
the haircut is zero. Equivalently, insisting on a positive haircut requires
that secured transactions occur at implicitly more ‘conservative’
asset valuations than the market price whenever [
,ψ)=ψ
the haircut is zero. Equivalently, insisting on a positive haircut requires
that secured transactions occur at implicitly more ‘conservative’
asset valuations than the market price whenever [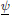 ,ψ].
,ψ].
This gives rise to an interesting trade-off. From Equation (33), it is clear that
the level of encumbrance, α, rises as
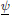 falls, for
falls, for
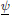 <ψ.
In turn, this gives a liquidity threshold of:
<ψ.
In turn, this gives a liquidity threshold of:

When the regulator reduces
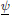 , or sets more
conservative haircuts, the liquidity position of the bank deteriorates if
, or sets more
conservative haircuts, the liquidity position of the bank deteriorates if
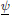 <ψ
in a narrow sense because the bank is forced to pledge more collateral to secured
creditors. But at the same time, there opens up a region for asset prices,
[
<ψ
in a narrow sense because the bank is forced to pledge more collateral to secured
creditors. But at the same time, there opens up a region for asset prices,
[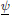 ,ψ],
over which changes in the market value of collateral
ψ have no effect on the bank's liquidity position. Asset prices
could fall to some level, ψ+ε, ε>0, without
affecting encumbrance and therefore liquidity.
,ψ],
over which changes in the market value of collateral
ψ have no effect on the bank's liquidity position. Asset prices
could fall to some level, ψ+ε, ε>0, without
affecting encumbrance and therefore liquidity.
In other words, haircut policy reduces the sensitivity of the bank's liquidity position to variation in asset prices over some range. The imposition of minimum haircut requirements can thus reduce the procyclical fluctuations generated by secured debt, with any narrow increase in liquidity risk arising from greater over-collateralisation potentially being dealt with by other regulatory tools (e.g. liquidity requirements). This is one of the key underpinnings of the recent international proposals to stipulate a framework of numerical haircut floors for certain securities financing transactions (FSB 2013b). Time-varying haircut policies have also been floated as an additional possibility to combat procyclicality (Bank of England 2011). Investigating such policies in this setting is an interesting question we plan to address in future research.
Our analysis makes a number of stark modelling assumptions to highlight some of the central trade-offs entailed in collateralised borrowing. Although our results are suggestive, there is clearly considerable scope to generalise – and endogenise – several features of the framework. Embedding the model in a system context and explicitly linking the fire sale price of the collateral asset to the state of the business cycle would materially enhance our understanding of the policy alternatives. We intend to explore these themes further in future research.
Footnotes
The views expressed herein are those of the authors and do not necessarily represent those of the Bank of England, its Financial Policy Committee or its Monetary Policy Committee. We would like to thank George Avil for excellent research assistance and Bernd Schwaab, Paul Tucker and participants at the RBA Annual Conference for helpful comments and suggestions. [*]
For a more detailed explanation of the role of haircuts, why these haircuts might fluctuate, and further empirical evidence, see Gorton and Metrick (2010). Additional empirical evidence of cyclicality in underlying haircuts is also given by Geanakoplos (2010) and Krishnamurthy (2010). [1]
If the expected value of date-2 returns is θ1 at date 1, and creditors observe noisy signals, xi = θ1 + σηi, with ηi distributed according to some density and σ governing the noise, there exists a unique equilibrium threshold signal x* above which creditors roll over and below which creditors withdraw. If θ1 is uniform, then a creditor in receipt of signal x* has a uniform belief over the proportion of withdrawals. [2]
The exogenous wedge r – rS > 0 entails a failure of the Modigliani-Miller theorem; the returns on secured and unsecured debt do not adjust to reflect their relative riskiness. This may reflect, for example, segmentation between the buyers of the two types of claim. [3]
The analysis would extend to the case in which secured creditors also guard against solvency risk. [4]
References
Adrian T and HS Shin (2010), ‘Liquidity and Leverage’, Journal of Financial Intermediation, 19(3), pp 418–437.
Anand K, J Chapman and P Gai (2012), ‘Covered Bonds, Core Markets, and Financial Stability’, Humboldt University, Collaborative Research Center, SFB 649 Discussion Paper 2012-065.
Bank of England (2011), ‘Instruments of Macroprudential Policy’, Discussion Paper, December.
Bank of England (2012), ‘3 Medium-Term Risks to Financial Stability’, in Financial Stability Report, 31, pp 30–46.
Brunnermeier MK and LH Pedersen (2009), ‘Market Liquidity and Funding Liquidity’, The Review of Financial Studies, 22(6), pp 2201–2238.
CGFS (Committee on the Global Financial System) (2010), The Role of Margin Requirements and Haircuts in Procyclicality, CGFS Papers No 36, Bank for International Settlements, Basel.
CGFS (2013), Asset Encumbrance, Financial Reform and the Demand for Collateral Assets, CGFS Papers No 49, Bank for International Settlements, Basel.
Enhanced Disclosure Task Force (2013), ‘Progress Report on the Level and Quality of the Implementation of “Enhancing the Risk Disclosures of Banks”’, 21 August.
Fransolet L and G Maraffino (2012), ‘The 3y LTROs: Who and Why?’, Global Rates Weekly, Barclays Capital, 2 March, pp 20–22.
FSB (Financial Stability Board) (2013a), ‘Progress and Next Steps Towards Ending “Too-Big-To-Fail” (TBTF)’, Report of the Financial Stability Board to the G-20, 2 September.
FSB (2013b), ‘Strengthening Oversight and Regulation of Shadow Banking: Policy Framework for Addressing Shadow Banking Risks in Securities Lending and Repos’, 29 August.
Gai P, A Haldane and S Kapadia (2011), ‘Complexity, Concentration and Contagion’, Journal of Monetary Economics, 58(5), pp 453–470.
Geanakoplos J (2010), ‘Solving the Present Crisis and Managing the Leverage Cycle’, Federal Reserve Bank of New York Economic Policy Review, 16(1), pp 101–131.
Gorton G and A Metrick (2010), ‘Haircuts’, Federal Reserve Bank of St. Louis Review, 92(6), pp 507–519.
Haldane A (2012), ‘Financial Arms Races’, Speech at the Institute for New Economic Thinking, The Centre for International Governance Innovation, and the Mercator Research Institute on Global Commons and Climate Change Third Annual Plenary Conference ‘Paradigm Lost: Rethinking Economics and Politics’, Berlin, 12–15 April.
Harrison M and S Samuels (2012), ‘Over Promising? Encumbrance at European Banks’, Equity Research, Barclays Capital, 8 March.
Juks R (2012), ‘Asset Encumbrance and its Relevance for Financial Stability’, Sveriges Riksbank Economic Review, 2012(3), pp 67–89.
Krishnamurthy A (2010), ‘How Debt Markets have Malfunctioned in the Crisis’, The Journal of Economic Perspectives, 24(1), pp 3–28.
Morris S and HS Shin (2003), ‘Global Games: Theory and Applications’, in M Dewatripont, LP Hansen and SJ Turnovsky (eds), Advances in Economics and Econometrics: Theory and Applications, Eighth World Congress, Econometric Society Monographs, Cambridge University Press, Cambridge, pp 56–114.
Morris S and HS Shin (2010), ‘Illiquidity Component of Credit Risk’, unpublished manuscript, Princeton University, February.
Rinaldi F (2011), ‘Ambiguity and Rollover Risk: A Possible Explanation for Market Freezes’, unpublished manuscript, Banque de France.
Roland I and R Sowerbutts (2013), ‘Driving Forces and Regulatory Treatment of Asset Encumbrance’, unpublished manuscript, Bank of England.