RBA Annual Conference – 2013 On the Economics of Committed Liquidity Facilities Morten L Bech and Todd Keister[*]
1. Introduction
As part of the regulatory response to the recent global financial crisis, the Basel Committee on Banking Supervision (BCBS) announced a new international regulatory framework for banks, known as Basel III. One important component of Basel III is the Liquidity Coverage Ratio (LCR), which aims to ensure that banks hold a more liquid portfolio of assets and rely on the central bank for funding only as a last resort. Specifically, the LCR requires each bank to hold a sufficient quantity of highly liquid assets to survive a 30-day period of market stress; this requirement is scheduled to be phased in gradually beginning in January 2015. In the process of designing and calibrating the LCR rules, it became clear that some jurisdictions do not have sufficient high-quality liquid assets (HQLA) for their banking system to meet this new requirement. Australia and South Africa are cases in point, as both have limited amounts of sovereign debt and other qualifying securities; see Debelle (2011), Heath and Manning (2012) and South African Reserve Bank (2012). In such jurisdictions, the regulation offers the central bank the option of providing, for an up-front fee, contractual committed liquidity lines that count toward a bank's stock of liquid assets. Stein (2013) argues that such lines have the potential to be a useful safety valve in other situations as well, since they can place an upper bound on the cost of the liquidity regulation.
This type of committed liquidity facility (CLF) is an innovation within central banking and raises several interesting questions. How should these facilities be designed and priced? How will they interact with other parts of central banks' missions? Should such facilities be used only in jurisdictions with a shortage of HQLA or should they be part of all central banks' toolkits? With a view to providing a framework for addressing these questions, we develop a model that extends our earlier work on implementing monetary policy in the presence of an LCR requirement (Bech and Keister 2013). We show how the LCR requirement can have significant side effects in a jurisdiction with a limited supply of HQLA, leading to a large regulatory liquidity premium and pushing the short-term interest rate to the floor of the central bank's rate corridor. Introducing a CLF allows the central bank to mitigate these effects, regardless of whether it is implemented as a fixed-price standing facility or using a fixed-quantity auction format. By pricing the CLF appropriately, the central bank can control either the equilibrium liquidity premium or the quantity of liquid assets held by banks, but not both. We argue that the optimal pricing arrangement will need to balance the costs of higher interest rate spreads against the benefits of having more liquid assets in the banking system and will depend on local bond market conditions. Moreover, given the uncertainty about equilibrium relationships in the new regulatory environment, we argue that central banks are likely to want to take a flexible approach to CLF pricing, adjusting terms as more experience is gained with this new policy tool.
We provide a brief overview of the new regulatory framework in the next section, then present our model in Section 3. We derive banks' demand for assets and CLF drawing rights in Section 4 and study equilibrium quantities and interest rates in Section 5. We use the model to discuss CLF pricing and related issues in Section 6 before concluding in Section 7.
2. The Regulatory Framework
In this section, we describe the regulations governing the LCR and the use of CLFs. Our discussion is based on the revised rules issued in January 2013 (BCBS 2013).
2.1 The Liquidity Coverage Ratio (LCR)
The LCR builds on traditional methodologies used internally by banks to assess exposure to contingent liquidity events. The regulation will require that a bank's stock of unencumbered HQLA be larger than its projected net cash outflows (NCOF) over a 30-day horizon under a stress scenario specified by supervisors; that is:
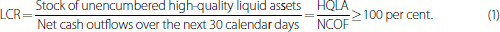
This requirement is scheduled to be phased in gradually, beginning with 60 per cent coverage in January 2015 and rising 10 percentage points each year to reach 100 per cent in January 2019.
Two types (or ‘levels’) of assets can be counted toward the calculation of HQLA in the numerator of the ratio. Level 1 assets include cash, central bank reserves and certain marketable securities backed by sovereigns and central banks; these assets can be used without limit to meet the requirement. Level 2 assets enter the calculation in a more restricted way and are divided into two subgroups. Level 2A assets include certain government securities, corporate debt securities and covered bonds, while Level 2B assets include lower-rated corporate bonds, residential mortgage-backed securities and equities that meet certain conditions. Level 2A assets can account for a maximum of 40 per cent of a bank's total stock of HQLA, whereas Level 2B assets can account for a maximum of 15 per cent of the total.
The denominator of the ratio, NCOF, is calculated by multiplying the size of various types of liabilities and off-balance sheet commitments by the rates at which they run off or are drawn down in the specified stress scenario. This scenario is designed to include a partial loss of retail deposits, significant loss of wholesale funding, contractual outflows from derivative positions associated with a three-notch ratings downgrade, and substantial calls on off-balance sheet exposures. From these outflows, banks are permitted to subtract expected inflows during the next 30 calendar days. In order to prevent banks from relying solely on anticipated inflows to meet their liquidity requirement, the fraction of outflows that can be offset this way is capped at 75 per cent.
2.2 Committed liquidity facilities (CLFs)
The LCR rules recognise that, in some jurisdictions, the relatively small stock of assets qualifying as HQLA could make implementing the LCR requirement problematic. Debelle (2011) describes the situation in Australia as follows:
[T]here is a marked shortage of high quality liquid assets that are outside the banking sector (that is, not liabilities of the banks). As a result of prudent fiscal policy over a large run of years at both the Commonwealth and state level, the stock of Commonwealth and state government debt is low. At the moment, the gross stock of Commonwealth debt on issue amounts to around 15 per cent of GDP, state government debt (semis) is around 12 per cent of GDP. These amounts fall well short of the liquidity needs of the banking system.
To address such situations, the BCBS has developed a number of policy options, one of which is for the central bank to operate a CLF.[1] The LCR rules specify that:
[T]hese facilities are contractual arrangements between the central bank and the commercial bank with a maturity date which, at a minimum, falls outside the 30-day LCR window … Such facilities are only permissible if there is also a fee for the facility which is charged regardless of the amount, if any, drawn down against that facility …(BCBS 2013, paragraph 58)
The Reserve Bank of Australia (RBA) and the South African Reserve Bank (SARB) have both indicated their intention to provide committed liquidity facilities and have published details on how the facilities are to be designed; the term sheets are summarised in Table 1. The two facilities are similar in many respects but differ in some dimensions. In both facilities, the up-front fee is lower than the spread between the rate for the central bank's standing lending facility and the target for the overnight rate. Moreover, both facilities charge banks the overnight lending facility rate for drawdowns and have limits on the usage of the facilities. The set of eligible collateral is larger than what is normally accepted at each central bank's other facilities. One key difference is that the up-front fee is fixed for the RBA but is determined by a progressive scale dependent on the quantity contracted for the SARB.
| Reserve Bank of Australia | South African Reserve Bank | |
|---|---|---|
| Pricing | ||
| Policy corridor | ±25 bps | ±100 bps |
| Up-front fee | fixed (15 bps) | scaled (15–45 bps) |
| Drawdown rate | = o/n lending facility rate | = o/n lending facility rate |
| Maximum amount | determined by supervisor | 40% of NCOF |
| Collateral | ||
| Assets eligible | > lending facility | > lending facility |
| Additional assets | self-securitised RMBS | self-securitised ABS |
| Haircuts | = other RBA facilities | = other SARB facilities |
|
Notes: RMBS denotes residential mortgage-backed securities, ABS denotes asset-backed securities Sources: RBA (2013); SARB (2012) |
||
3. The Model
The analysis here builds on Bech and Keister (2013), which studies monetary policy implementation in the presence of an LCR requirement.[2] We introduce two new features into this framework: (i) banks' asset portfolios are endogenous rather than fixed; and (ii) the central bank operates a CLF. In this section, we describe the role of banks and of the various markets in the model, as well as the basic design features of the CLF.
3.1 Banks
There is a continuum of identical banks, indexed by i ∈ [0,1], all of which behave competitively in the sense that they take market interest rates as given and aim to maximise expected profits.
3.1.1 Balance sheets and decisions
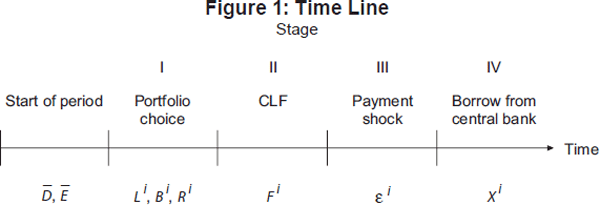
The model plays out over the course of a period with four stages. Bank i begins the period with a balance sheet of the form:
| Assets | Liabilities | ||
|---|---|---|---|
| Loans | Li | Deposits |
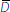 |
| Bonds | Bi | ||
| Reserves | Ri | Equity |
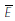 |
To simplify the analysis, we take the values of deposits
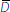 and equity
and equity
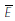 as given; these values are determined
by activities outside the scope of the model. In the first stage, banks distribute
their fixed resources across the three assets shown in the balance sheet: loans,
bonds, and reserves. In the second stage, the central bank offers banks an
opportunity to acquire rights to draw funds under its CLF. Let F i
denote the quantity of such rights acquired by bank i, which is an
off-balance-sheet item. After the CLF has closed, each bank experiences a payment
shock in which an amount ε i of customer deposits
is sent as a payment to another bank. If ε i is
negative, the shock represents an inflow of funds. The value of ε i
is drawn from a common, symmetric distribution G with zero mean. Depending
on the size of this shock, a bank may need to borrow from the central bank
to meet its regulatory requirements. This borrowing takes place in the fourth
and final stage; let X i ≥ 0 denote the amount
borrowed.[3]
Bank i's end-of-period balance sheet is then:
as given; these values are determined
by activities outside the scope of the model. In the first stage, banks distribute
their fixed resources across the three assets shown in the balance sheet: loans,
bonds, and reserves. In the second stage, the central bank offers banks an
opportunity to acquire rights to draw funds under its CLF. Let F i
denote the quantity of such rights acquired by bank i, which is an
off-balance-sheet item. After the CLF has closed, each bank experiences a payment
shock in which an amount ε i of customer deposits
is sent as a payment to another bank. If ε i is
negative, the shock represents an inflow of funds. The value of ε i
is drawn from a common, symmetric distribution G with zero mean. Depending
on the size of this shock, a bank may need to borrow from the central bank
to meet its regulatory requirements. This borrowing takes place in the fourth
and final stage; let X i ≥ 0 denote the amount
borrowed.[3]
Bank i's end-of-period balance sheet is then:
| Assets | Liabilities | ||
|---|---|---|---|
| Loans | Li | Deposits |
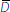 −εi −εi |
| Bonds | B i | Central bank borrowing | Xi |
| Reserves | Ri −εi + Xi | Equity |
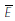 |
Figure 1 illustrates the sequence of events and summarises when banks choose each decision variable.
3.1.2 The reserve requirement
Each bank faces a reserve requirement of the form:

The left-hand side of this expression is the bank's reserve holdings at the end
of the period, taking into account the payment shock and any borrowing from
the central bank. The right-hand side is the requirement for the period. To
conserve on notation, we study a system with no reserve requirements by setting
 to zero, so that Equation (2) simply
requires each bank to avoid an overdraft in its reserve account at the end
of the period. If the bank were to violate this requirement after the realisation
of the payment shock, it would borrow funds from the central bank to ensure
that Equation (2) held.
to zero, so that Equation (2) simply
requires each bank to avoid an overdraft in its reserve account at the end
of the period. If the bank were to violate this requirement after the realisation
of the payment shock, it would borrow funds from the central bank to ensure
that Equation (2) held.
3.1.3 The LCR requirement
In the context of our model, bank i's LCR requirement is:

Recall from Equation (1) that the numerator of the ratio is the total value of the bank's HQLA (its end-of-period holdings of bonds and reserves) plus any rights to draw on the CLF it has purchased. The denominator measures the 30-day NCOF assumed under the stress scenario, which in our model equals a fraction θ > 0 of the bank's deposits.[4] Notice that contracting with the CLF (increasing F i) has the same effect on a bank's LCR as holding more bonds (increasing B i ).
3.1.4 Bank profits
The bank earns the interest rates rL and rB on its loans and bond holdings, respectively, and pays an interest rate rD on customer deposits. The bank pays the central bank φ per unit of CLF rights purchased. It earns rR on any positive reserve balances and faces a penalty rate rX > rR for any funds borrowed from the central bank's overnight lending facility.
In comparing interest rates across assets, differences in credit risk and liquidity risk are clearly important. To account for these differences, we introduce a fixed premium τ that reflects both the credit and liquidity risk associated with loans in our model, so that the risk-adjusted benefit to the bank of making a unit of loans is given by rL – τ. We assume that bonds and reserves are both short-term, risk-free assets and, hence, the premium associated with these assets is zero.[5] Bank i's profit for the period, net of credit and liquidity risk, can then be written as:
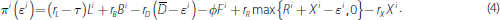
Note that the quantity of CLF rights purchased affects two terms in this expression: it creates an expense of φ F i and it potentially decreases the amount X i of borrowing from the central bank.
3.2 Markets
To help maintain tractability, we assume that the markets in which banks trade in
Stage I of Figure 1 are competitive and operate without frictions. We assume
the loan market is completely passive – banks can make whatever quantity
of loans they want at the equilibrium interest rate  . We describe the markets
for reserves and bonds below.
. We describe the markets
for reserves and bonds below.
3.2.1 The market for reserves
The central bank determines the total supply of reserves
 at the beginning of the
period.[6]
To simplify our analysis, we assume the central bank sets the supply of reserves
equal to total required reserves, which implies:
at the beginning of the
period.[6]
To simplify our analysis, we assume the central bank sets the supply of reserves
equal to total required reserves, which implies:
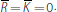
In an environment with no LCR requirement, this policy would steer the overnight interest rate to the midpoint of the central bank's corridor [rR, rX] in the standard way (see, for example, Whitesell (2006)). We denote this midpoint by

and note that, in the absence of an LCR requirement,
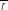 would be the risk-free, short-term
interest rate in the economy.
would be the risk-free, short-term
interest rate in the economy.
3.2.2 The bond market
An important goal of our model is to determine how the quantity of bonds held by
banks depends on the LCR requirement and on the design features of the CLF.
Any bonds not held by banks are held by non-bank entities, including other
financial institutions, households and foreign entities. We assume that the
total quantity of bonds in the economy is fixed at
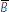 and that the demand for bonds by non-bank
entities is a continuous, weakly increasing function of the interest rate rB.
As a result, the supply of bonds to the banking sector – that is, the
quantity of bonds not held by non-banks – is a continuous, weakly decreasing
function of rB. We denote this supply function by μ(B).
While we allow this function to take many different shapes, we impose one regularity
condition to simplify the analysis:
and that the demand for bonds by non-bank
entities is a continuous, weakly increasing function of the interest rate rB.
As a result, the supply of bonds to the banking sector – that is, the
quantity of bonds not held by non-banks – is a continuous, weakly decreasing
function of rB. We denote this supply function by μ(B).
While we allow this function to take many different shapes, we impose one regularity
condition to simplify the analysis:

This condition states that if all bonds are held outside the banking system, their interest rate will equal the midpoint of the central bank's interest rate corridor. It implies that, in the absence of an LCR requirement, bonds would earn the same rate of return as other risk-free assets.[7]
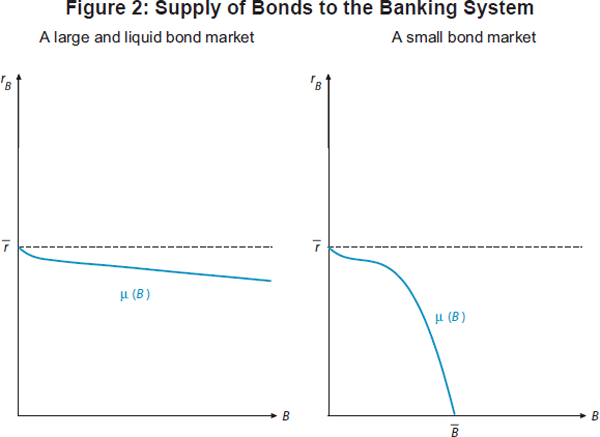
Figure 2 depicts two different bond supply functions. In the left-hand panel, the
bond market is both large and liquid in the sense that banks' purchases
of bonds have relatively little effect on their price. In this situation, the
interest rate on bonds remains close to
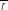 over a wide range of bond holdings
by banks. The right-hand panel, in contrast, depicts a situation in which the
total quantity of bonds
over a wide range of bond holdings
by banks. The right-hand panel, in contrast, depicts a situation in which the
total quantity of bonds
 is much smaller and the demand for
bonds by non-banks is inelastic in some regions. This panel captures important
features of the market for government bonds in jurisdictions like Australia
where, according to Davis (2011, p 5), ‘[a]s banks attempt to increase
their holdings of government debt, their demand will drive down its yield relative
to other investments’. Debelle (2013) adds that ‘[a]t some point,
the scarcity of available [government debt] securities would cause their yields
to fall to a particularly low level’. In the analysis below, we show
how the effect of introducing an LCR requirement depends crucially on the shape
of the bond supply function μ, which may vary over time as well
as across countries.
is much smaller and the demand for
bonds by non-banks is inelastic in some regions. This panel captures important
features of the market for government bonds in jurisdictions like Australia
where, according to Davis (2011, p 5), ‘[a]s banks attempt to increase
their holdings of government debt, their demand will drive down its yield relative
to other investments’. Debelle (2013) adds that ‘[a]t some point,
the scarcity of available [government debt] securities would cause their yields
to fall to a particularly low level’. In the analysis below, we show
how the effect of introducing an LCR requirement depends crucially on the shape
of the bond supply function μ, which may vary over time as well
as across countries.
3.3 The committed liquidity facility (CLF)
In general terms, the design of the CLF is characterised by a non-decreasing price function φ(F) that specifies the fee the central bank will charge for CLF rights if the total quantity of rights purchased by all banks is F. We assume that CLF rights are allocated in a competitive fashion, meaning that each bank takes the fee φ as given when choosing the quantity of rights to purchase. Our model can be generalised to allow for non-competitive allocation rules or for pricing rules in which each bank faces an increasing fee schedule depending on the amount borrowed, but we restrict our attention to the simpler, linear case here.
We focus on two specific designs for the CLF. The first is a fixed-price standing
facility in which each bank can purchase as many CLF rights as it wants at
a given price  ; this design corresponds
to setting φ(F)=
; this design corresponds
to setting φ(F)=
 for all F. The second design
we consider is a fixed-quantity auction, where the central bank offers a quantity
for all F. The second design
we consider is a fixed-quantity auction, where the central bank offers a quantity
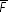 of CLF rights and is willing to accept
whatever fee emerges from the auction. In the analysis below, we show that
these two designs lead to equivalent outcomes in our model.
of CLF rights and is willing to accept
whatever fee emerges from the auction. In the analysis below, we show that
these two designs lead to equivalent outcomes in our model.
4. Optimal Portfolio Choices
In this section, we derive a typical bank's demand for each of the three assets and for CLF rights. We begin with Stage IV in the time line in Figure 1, where each bank determines how much to borrow from the central bank's standing facility at the end of the period. This borrowing rule allows us to derive a bank's expected profit before the payment shock is realised, which is the objective the bank seeks to maximise when making its decisions in Stages I and II.
4.1 Borrowing from the central bank
Borrowing from the central bank is costly and, therefore, each bank will choose to
borrow the minimum amount needed to meet its regulatory requirements. Let
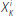 denote the minimum amount bank i
must borrow from the central bank to fulfill the reserve requirement in Equation
(2):
denote the minimum amount bank i
must borrow from the central bank to fulfill the reserve requirement in Equation
(2):

Let
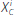 denote the minimum amount bank i
must borrow to fulfill the LCR requirement in Equation (3):
denote the minimum amount bank i
must borrow to fulfill the LCR requirement in Equation (3):

Bank i's total borrowing from the central bank X i will be the minimum amount needed to fulfill both of these requirements; that is:

Figure 3 depicts X i as a function of the realised payment shock ε i together with a density function g for this shock. The light blue curve in each panel represents Equation (7), the borrowing needed to satisfy the reserve requirement, which is positive whenever ε i is larger than

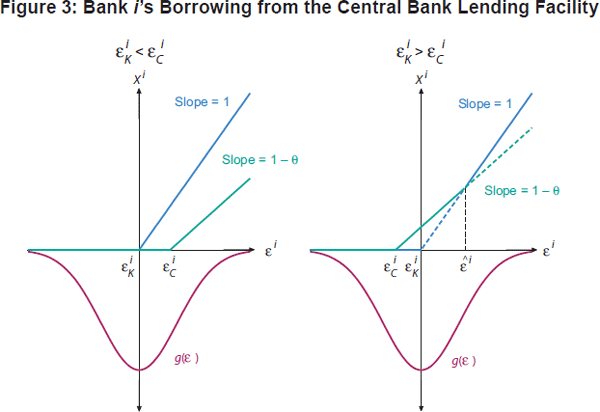
The green curve represents Equation (8), the borrowing needed to satisfy the LCR requirement, which is positive for values of ε i larger than:

The bank's borrowing X i is the upper envelope of these two curves.
As Figure 3 shows, two distinct cases arise. In the left-hand panel of Figure 3,
the elements of the bank's balance sheet are such that
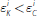 . In this case, the borrowing needed
to satisfy the bank's reserve requirement is always sufficient to ensure
that the bank also satisfies its LCR requirement, even when ε i
is larger than
. In this case, the borrowing needed
to satisfy the bank's reserve requirement is always sufficient to ensure
that the bank also satisfies its LCR requirement, even when ε i
is larger than
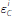 . In other words, the amount borrowed
from the central bank's lending facility is determined solely by the bank's
need to meet its reserve requirement in this case; the LCR requirement is never
a binding concern. In contrast, the right-hand panel depicts a situation where
the balance sheet is such that
. In other words, the amount borrowed
from the central bank's lending facility is determined solely by the bank's
need to meet its reserve requirement in this case; the LCR requirement is never
a binding concern. In contrast, the right-hand panel depicts a situation where
the balance sheet is such that
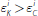 holds. In this case, the amount borrowed
from the central bank is determined by the need to meet the LCR requirement
if ε i falls in the interval
holds. In this case, the amount borrowed
from the central bank is determined by the need to meet the LCR requirement
if ε i falls in the interval
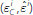 , where
, where

and by the need to meet the reserve requirement when ε i is larger
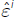 .
.
4.2 Expected profit
The expected value of bank i's profit defined in Equation (4) can, using E[ε i] = 0 and rearranging terms, be written as:
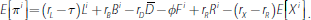
Using the definition of X i in Equation (9), we can rewrite this expression as
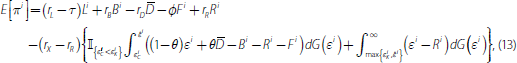
where the indicator function
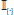 takes the value one if the expression
{.} is true and zero otherwise. In making its decisions in Stages I and II
of Figure 1, bank i will aim to maximise the value of Equation (13).
We derive the optimal choices in each of these stages below.
takes the value one if the expression
{.} is true and zero otherwise. In making its decisions in Stages I and II
of Figure 1, bank i will aim to maximise the value of Equation (13).
We derive the optimal choices in each of these stages below.
4.3 The demand for bonds and reserves
In Stage I, bank i divides its initial resources from deposits and equity between loans, bonds and reserves, subject to the balance sheet constraint:

We use this constraint to replace Li in Equation (13) and focus on the choices of B i and R i. To account for the indicator function in this objective function, we look at the first-order conditions separately in two distinct regions of the feasible set.
First, consider values of (B i, R i) such that
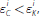 which corresponds to the situation
in the right-hand panel of Figure 3. In this region, the indicator function
is one, we have max
which corresponds to the situation
in the right-hand panel of Figure 3. In this region, the indicator function
is one, we have max
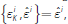 and the first-order conditions that
characterise a solution
are[8]
and the first-order conditions that
characterise a solution
are[8]
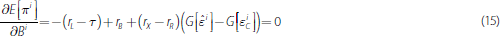
and
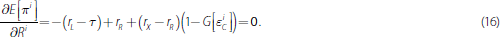
Equation (15) says the marginal income lost from holding bonds instead of loans,
rL − τ −
rB, must equal the marginal benefit
bonds provide in meeting the LCR requirement. When ε i falls
in the interval
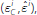 holding an extra dollar's worth
of bonds allows the bank to borrow one dollar less from the central bank, saving
it the net cost (rX −
rR). Similarly, Equation (16) states that the marginal
income lost from holding reserves, rL
− τ − rR, is equal
to the marginal benefit reserves provide in terms of meeting both the LCR requirement
and the reserve requirement. As shown in the right-hand panel of Figure 3,
holding an additional dollar of reserves allows the bank to borrow one dollar
less from the central bank whenever the payment shock is larger than
holding an extra dollar's worth
of bonds allows the bank to borrow one dollar less from the central bank, saving
it the net cost (rX −
rR). Similarly, Equation (16) states that the marginal
income lost from holding reserves, rL
− τ − rR, is equal
to the marginal benefit reserves provide in terms of meeting both the LCR requirement
and the reserve requirement. As shown in the right-hand panel of Figure 3,
holding an additional dollar of reserves allows the bank to borrow one dollar
less from the central bank whenever the payment shock is larger than
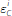 .
.
Next, consider the region where
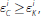 which corresponds to the left-hand
panel of Figure 3. In this case, the value of the indicator function is zero,
we have max
which corresponds to the left-hand
panel of Figure 3. In this case, the value of the indicator function is zero,
we have max
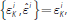 and the first-order conditions are
and the first-order conditions are

and
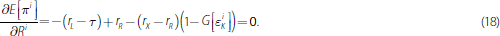
Notice that Equation (17) implies rL – τ = rB must hold for the solution of the bank's problem to fall in this region. Since the LCR requirement is never a binding concern in this region, Equation (18) implies that the lost income from holding reserves instead of loans, rL – τ – rR, must equal the marginal benefit reserves provide simply in terms of meeting the reserve requirement. The following proposition combines these two cases and characterises the bank's optimal portfolio choice in Stage I of Figure 1.
Proposition 1. Bank i will choose (Bi,Ri) so that the critical values
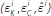 defined in Equations (10) to (12) satisfy
defined in Equations (10) to (12) satisfy

and

4.4 The demand for CLF rights
In Stage II of Figure 1, bank i will choose to purchase a quantity
F i ≥ 0 of CLF rights, again with the objective of maximising
Equation (13). In the region where
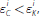 the first-order condition characterising
the optimal choice is
the first-order condition characterising
the optimal choice is
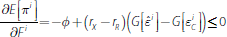
with equality if F i > 0. In this region, which again corresponds to
the right-hand panel in Figure 3, purchasing CLF rights helps mitigate the
bank's LCR shortfall when the realisation of the payment shock is between
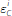 and
and
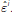 Notice the similarity between this
condition and Equation (15), which reflects the fact that holding bonds and
purchasing CLF rights offer the same benefit in terms of increasing the bank's
LCR. The bank will choose to purchase CLF rights only if the fee φ
is no larger than the income loss associated with holding bonds, rL
− τ − rB.
Notice the similarity between this
condition and Equation (15), which reflects the fact that holding bonds and
purchasing CLF rights offer the same benefit in terms of increasing the bank's
LCR. The bank will choose to purchase CLF rights only if the fee φ
is no larger than the income loss associated with holding bonds, rL
− τ − rB.
In the region where 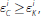 the marginal benefit
of CLF rights is given by
the marginal benefit
of CLF rights is given by
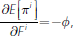
which is always negative. This region again corresponds to the left-hand panel in Figure 3, where the LCR is never a binding concern and, as a result, CLF rights have no value for the bank. If the solution to the bank's optimisation problem lies in this region, it will necessarily have F i = 0. The following proposition formalises these results.
Proposition 2. Bank i's demand for CLF rights is given by:
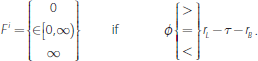
This result shows a tight relationship between the CLF fee φ and the opportunity cost of holding bonds, rL – τ – rB. If purchasing CLF rights is more expensive than holding bonds, banks will not use the CLF. If purchasing CLF rights is cheaper than holding bonds, banks will demand as many CLF rights as possible, selling bonds to compensate. In the middle case, banks are indifferent at the margin between holding bonds and purchasing CLF rights for the purpose of satisfying the LCR requirement.
5. Equilibrium
In this section, we derive the equilibrium interest rates and portfolio choices. After providing a formal definition of equilibrium, we analyse outcomes in a benchmark setting with no liquidity regulation, then in a setting with an LCR requirement but no CLF, and finally in a setting where a CLF is introduced.
5.1 Definition
Since there is a unit measure of banks, all of whom face the same decision problem, the aggregate demand for loans, bonds, reserves and CLF rights are the same as the individual demands derived above. Equilibrium requires that each of these demands equals the corresponding supply of the asset to the banking system, as specified in the following definition.
Definition: An equilibrium consists of a portfolio choice for banks
(L*, B*, R*, F*) together with interest rates
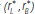 and a CLF fee φ* such that:
and a CLF fee φ* such that:
- each bank's choices (L*, B*, R*, F*) maximise its expected profit (Equation (13)) subject to the balance sheet constraint in Equation (14), taking the interest rates and CLF fee as given
-
markets clear, that is

-
CLF rights are priced according to the central bank's rule,
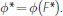
Using the market-clearing conditions in Equation (21), we can write the equilibrium values of the critical points for the payment shock defined in Equations (10) to (12) as:
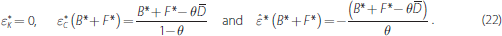
Note that
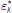 depends only on the central bank's
choice for the quantity of excess reserves, which we have assumed to be zero.
In contrast, both
depends only on the central bank's
choice for the quantity of excess reserves, which we have assumed to be zero.
In contrast, both
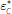 and
and 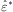 are functions of the
sum of banks' bond holdings and CLF rights, B* + F*, which is
determined as part of the equilibrium.
are functions of the
sum of banks' bond holdings and CLF rights, B* + F*, which is
determined as part of the equilibrium.
5.2 Equilibrium with no liquidity regulation
We begin by studying the properties of equilibrium in a benchmark case where there
is no liquidity regulation, which corresponds to setting the run-off rate θ
in our model to zero. In this case, the critical values in
Equation (22) will always satisfy
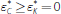 and, hence, the configuration is always
like that in the left-hand panel of Figure 3. In other words, when there is
no LCR requirement, banks' only liquidity management concern in our model
is satisfying the reserve requirement in Equation (2). The following proposition
characterises the equilibrium outcome in this case.
and, hence, the configuration is always
like that in the left-hand panel of Figure 3. In other words, when there is
no LCR requirement, banks' only liquidity management concern in our model
is satisfying the reserve requirement in Equation (2). The following proposition
characterises the equilibrium outcome in this case.
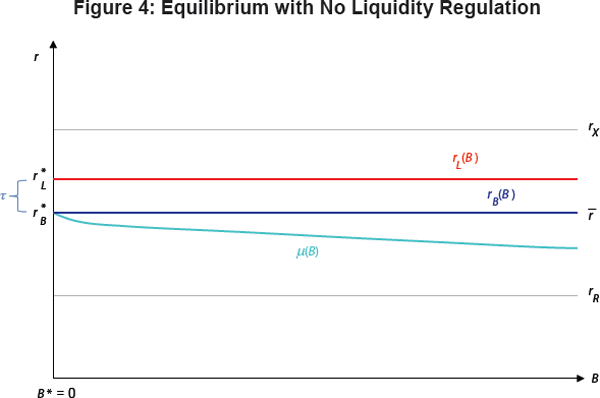
Proposition 3. When there is no LCR requirement, equilibrium interest rates satisfy:
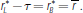
When there is no liquidity regulation, the short-term, risk-free interest rate equals
the midpoint of the central bank's corridor,
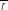 , as in Whitesell (2006) and others.
The interest rate on loans is given by
, as in Whitesell (2006) and others.
The interest rate on loans is given by
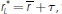 which implies that the premium τ
can be interpreted as the market price of credit and liquidity risk.
which implies that the premium τ
can be interpreted as the market price of credit and liquidity risk.
Figure 4 illustrates this result. The dark blue line in Figure 4 corresponds to banks'
demand for bonds from Equation (19). When there is no LCR requirement, this
equation simply says that banks are willing to hold bonds only if the return
they offer is at least equal to the risk-free rate. For this reason, the demand
curve is flat at 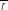 . Similarly, the red
line represents banks' demand for loans from Equation (20). Since banks
are willing to hold loans only if the net return rL −
τ is at least equal to the market risk-free rate, this demand
curve is flat at
. Similarly, the red
line represents banks' demand for loans from Equation (20). Since banks
are willing to hold loans only if the net return rL −
τ is at least equal to the market risk-free rate, this demand
curve is flat at
 + τ. The light blue curve
represents the supply of bonds to the banking system μ(B).
Equilibrium occurs when this supply curve crosses the dark blue demand curve,
which happens here at B* = 0. In other words, given this particular
function μ, banks will hold no bonds in equilibrium in the absence
of liquidity
regulation.[9]
+ τ. The light blue curve
represents the supply of bonds to the banking system μ(B).
Equilibrium occurs when this supply curve crosses the dark blue demand curve,
which happens here at B* = 0. In other words, given this particular
function μ, banks will hold no bonds in equilibrium in the absence
of liquidity
regulation.[9]
To the extent that holdings of liquid assets by banks provide external benefits, it might be desirable to introduce liquidity regulation to the situation depicted in Figure 4. One can think of the objective of such regulation as being twofold: (i) encouraging banks to hold a more liquid portfolio of assets; and (ii) correcting the possible underpricing of liquidity risk in markets. Stein (2013) puts it this way:
[A]s the financial crisis made painfully clear, the business of liquidity provision inevitably exposes financial intermediaries to various forms of run risk … [F]ire sales and bank failures – and the accompanying contractions in credit availability – can have spillover effects to other financial institutions and to the economy as a whole. Thus, while banks will naturally hold buffer stocks of liquid assets to handle unanticipated outflows, they may not hold enough because, although they bear all the costs of this buffer stocking, they do not capture all of the social benefits, in terms of enhanced financial stability and lower costs to taxpayers in the event of failure. It is this externality that creates a role for policy.
An LCR requirement is one policy tool that can be used to address these issues.
5.3 Equilibrium with an LCR requirement
We now study how the equilibrium changes when banks are subject to the LCR requirement in Equation (3) with a run-off rate on deposits of θ > 0, but there is no CLF. The following proposition characterises the equilibrium outcome.
Proposition 4. When there is an LCR requirement but no CLF, equilibrium bond holdings B* are implicitly defined by
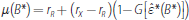
and equilibrium interest rates satisfy
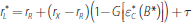
and
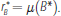
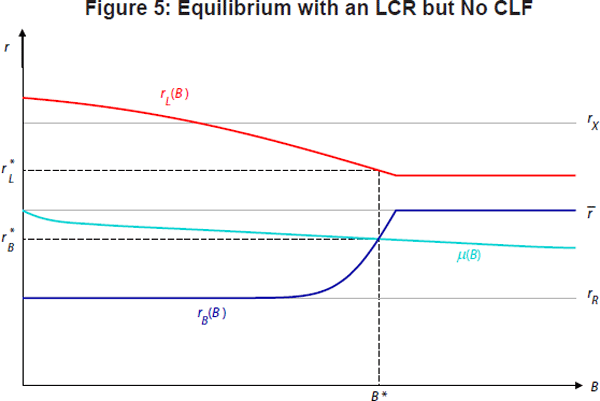
This result and its implications are illustrated in Figure 5. The dark blue curve again corresponds to banks' demand for bonds from Equation (19), which we rewrite here as an explicit function of B using the equilibrium critical points in Equation (22) with F* set to zero,

When banks' bond holdings are low,
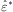 is positive and the curve is an increasing
function of B. Once the level of bond holdings reaches θ
is positive and the curve is an increasing
function of B. Once the level of bond holdings reaches θ
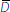 , however, banks are holding enough
bonds to ensure that the LCR requirement is never a binding concern. Beyond
this point, banks are willing to hold additional bonds only when the yield
is at least
, however, banks are holding enough
bonds to ensure that the LCR requirement is never a binding concern. Beyond
this point, banks are willing to hold additional bonds only when the yield
is at least
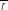 . Similarly, using Equations (20) and
(22), we can write the relationship between the loan rate rL
and the quantity of bonds held by banks as
. Similarly, using Equations (20) and
(22), we can write the relationship between the loan rate rL
and the quantity of bonds held by banks as

This relationship corresponds to the red curve in Figure 5. When B is less than θ
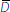 ,
,
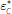 is negative and the curve lies above
the rate
is negative and the curve lies above
the rate
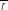 . As B increases, the likelihood
of an LCR deficiency falls and, therefore, the spread between the loan rate
and
. As B increases, the likelihood
of an LCR deficiency falls and, therefore, the spread between the loan rate
and
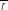 gradually declines, reaching τ
at B=θ
gradually declines, reaching τ
at B=θ
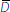 .
.
Equilibrium is determined by the intersection of the demand curve in Equation (23)
with the supply curve for bonds μ(B), which is again represented by the light blue curve
in Figure 5. Equilibrium bond holdings are denoted by B*
and the equilibrium interest rate on bonds by
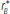 . The equilibrium loan rate is determined
by the corresponding point on the red curve, denoted
. The equilibrium loan rate is determined
by the corresponding point on the red curve, denoted
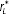 . Notice that once an LCR requirement
is introduced, we have the strict ordering:
. Notice that once an LCR requirement
is introduced, we have the strict ordering:
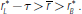
In other words, the LCR requirement raises the equilibrium loan rate
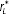 while lowering the equilibrium interest
rate on bonds
while lowering the equilibrium interest
rate on bonds
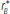 .[10]
The spread
.[10]
The spread
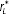 −
−
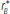 now has two components: the original
premium τ
is augmented by a regulatory liquidity premium that reflects the equilibrium value
banks place on bonds for the purposes of meeting the LCR requirement. Using
Equations (23) and (24), we can write this spread as:
now has two components: the original
premium τ
is augmented by a regulatory liquidity premium that reflects the equilibrium value
banks place on bonds for the purposes of meeting the LCR requirement. Using
Equations (23) and (24), we can write this spread as:
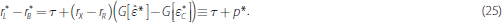
The regulatory liquidity premium, denoted p*, equals the probability of the LCR being a binding concern for each bank (see the right-hand panel of Figure 3) multiplied by the net cost of borrowing an additional dollar from the central bank to meet this requirement. Note that while the additional premium raises the cost of credit – that is, loans in the economy – this outcome may be desirable if liquidity was thought to be underpriced before the regulation was put in place.
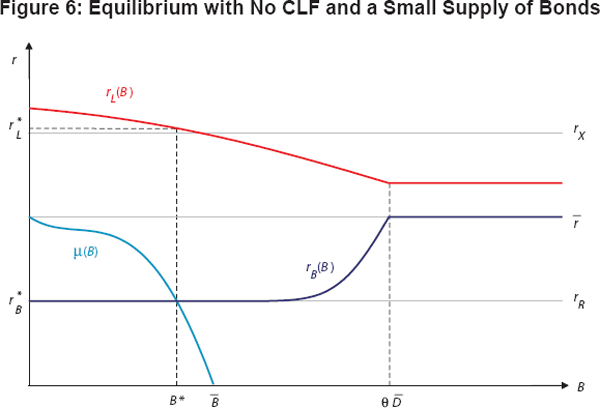
Figure 6 depicts the effects of an LCR requirement for an economy with a more limited
supply of bonds. The increase in banks' bond holdings generated by the
regulation is necessarily much smaller in this case than in
Figure 5, while the increase in the spread
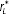 −
−
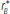 is much larger. In fact, banks'
demand to hold bonds for LCR purposes in this case pushes the equilibrium interest
rate on bonds down to the floor of the central bank's corridor at rR.
The scarcity of bonds in the economy implies that banks will often find themselves
facing an LCR deficiency and, hence, needing to borrow reserves from the central
bank to meet this requirement. These borrowed reserves perform double duty
in the sense that they count toward both a bank's LCR requirement and its
reserve requirement. As a result of this borrowing, therefore, banks become
virtually certain to over-satisfy their reserve requirements, which implies
that bonds and reserves become near-perfect substitutes. In other words, introducing
an LCR requirement in this economy causes the short-term interest rate to fall
and thereby affects the implementation of monetary policy. In effect, the central
bank in this scenario ends up operating a ‘floor system’ of monetary
policy
implementation.[11]
Debelle (2011) discusses these concerns:
is much larger. In fact, banks'
demand to hold bonds for LCR purposes in this case pushes the equilibrium interest
rate on bonds down to the floor of the central bank's corridor at rR.
The scarcity of bonds in the economy implies that banks will often find themselves
facing an LCR deficiency and, hence, needing to borrow reserves from the central
bank to meet this requirement. These borrowed reserves perform double duty
in the sense that they count toward both a bank's LCR requirement and its
reserve requirement. As a result of this borrowing, therefore, banks become
virtually certain to over-satisfy their reserve requirements, which implies
that bonds and reserves become near-perfect substitutes. In other words, introducing
an LCR requirement in this economy causes the short-term interest rate to fall
and thereby affects the implementation of monetary policy. In effect, the central
bank in this scenario ends up operating a ‘floor system’ of monetary
policy
implementation.[11]
Debelle (2011) discusses these concerns:
[O]ne possible solution to the shortage of level 1 assets would be for banks to significantly increase the size of their [reserve holdings] to meet their liquidity needs. While this is possible, it would mean that the RBA's balance sheet would increase considerably. The RBA would have to determine what assets it would be willing to hold against the increase in its liabilities, and would be confronted by the same problem of the shortage of assets in Australia outside the banking system.
… [T]his outcome would also significantly affect the ability to meet the cash rate target set by the Reserve Bank Board. That is, we do not want to impair the operational framework for monetary policy which has served us well for many years.
It is precisely to mitigate these problems that the LCR rules permit central banks in certain jurisdictions to operate a CLF.
5.4 Equilibrium with a CLF
We now ask how the equilibrium of the model changes when the central bank introduces a committed liquidity facility. The facility is characterised by a non-decreasing price function φ(F) as described in Section 3.3. We first show that if the fee for CLF rights is set sufficiently high, banks do not use the facility and the equilibrium outcome is the same as when there is no CLF.
Proposition 5. If φ (0) ≥ p*, the CLF is not used in equilibrium,
F* = 0. Equilibrium bond holdings B* and interest rates
(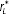 ,
,
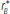 ) are as given in Proposition 4.
) are as given in Proposition 4.
Recall that p*, as defined in Equation (25), represents the regulatory liquidity premium that arises in the absence of a CLF. If the fee for purchasing CLF rights is larger than this premium, it would be less expensive for a bank to increase its LCR by holding more bonds and fewer loans than by using the CLF. In such a situation, the CLF will see no activity. The next proposition characterises how the equilibrium allocation changes when the CLF is priced in a way that attracts usage.
Proposition 6. If φ (0) < p*, then the equilibrium quantities (B*, F*) are defined by

and
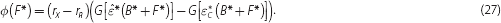
The equilibrium interest rates and CLF fee satisfy


and

Equation (26) requires that the supply of bonds to the banking system equal banks' demand for bonds, taking into account the fact that this demand depends on CLF usage F*. Equation (27) requires that the CLF fee equals the size of the regulatory liquidity premium that arises in equilibrium, which ensures that banks are willing to use the facility.
As discussed above, banks can increase their stock of HQLA either by holding more
bonds or by holding loans and purchasing CLF rights. The net yield from the
latter approach is given by the net yield on loans,
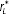 − τ, minus the CLF
fee φ *. Using Equations (27), (28) and (30), we can write this
yield as
− τ, minus the CLF
fee φ *. Using Equations (27), (28) and (30), we can write this
yield as
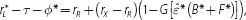
which, from Equations (26) and (29), is exactly
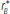 . In other words, these two ways of
increasing a bank's HQLA must generate the same return. This result relates
to the rules on CLF pricing, which state:
. In other words, these two ways of
increasing a bank's HQLA must generate the same return. This result relates
to the rules on CLF pricing, which state:
… the fee [should be] set so that banks which claim the facility line to meet the LCR, and banks which do not, have similar financial incentives to reduce their exposure to liquidity risk. That is, the fee should be set so that the net yield on the assets used to secure the facility should not be higher than the net yield on a representative portfolio of Level 1 and Level 2 assets, after adjusting for any material differences in credit risk. (BCBS 2013, paragraph 58)
Proposition 6 shows that, at least in our model environment, when the CLF is active the fee φ * will always be such that these two net yields are equal, because the equilibrium returns on assets will necessarily adjust so that this relationship holds.
Next, we illustrate the results from Proposition 6 in more detail by studying particular forms of the CLF pricing function φ (F).
5.4.1 A fixed-price standing facility
Suppose the central bank sets
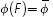 for all F, thereby operating
the CLF as a standing facility in which banks can purchase as many rights as
they choose at a fixed per-unit fee. Figure 7 illustrates the equilibrium outcome
under this type of facility. Recall from Equation (22) that the equilibrium
critical values of the payment
shock (
for all F, thereby operating
the CLF as a standing facility in which banks can purchase as many rights as
they choose at a fixed per-unit fee. Figure 7 illustrates the equilibrium outcome
under this type of facility. Recall from Equation (22) that the equilibrium
critical values of the payment
shock (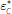 ,
,
 ) – and hence the demand
curve in Equation (23) – now depend on the sum of the bank's
holdings of bonds and CLF rights:
) – and hence the demand
curve in Equation (23) – now depend on the sum of the bank's
holdings of bonds and CLF rights:
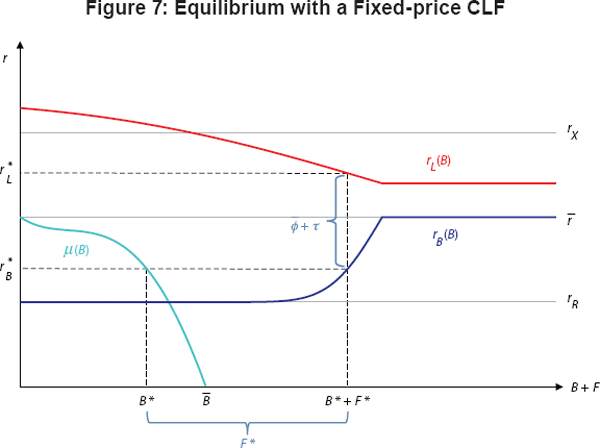
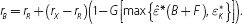
The dark blue curve in Figure 7 is thus the same as in Figures 5 and 6, but the variable being measured on the horizontal axis is now B + F rather than B alone. Similarly, the red curve has the same shape as in the earlier figures, but now relates the loan rate rL to the sum B + F.
Combining Equations (26) to (30) shows that

must hold in equilibrium. As shown in Figure 7, there is a unique value of B + F such that the gap between the red and dark blue curves
is exactly
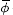 +τ. Equation (31) thus
determines the equilibrium sum B* +
F* and the equilibrium interest rates
+τ. Equation (31) thus
determines the equilibrium sum B* +
F* and the equilibrium interest rates
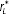 and
and
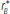 . The equilibrium quantity of bonds
held by banks, B*, is then determined by the supply of bonds μ(B)
at the interest rate
. The equilibrium quantity of bonds
held by banks, B*, is then determined by the supply of bonds μ(B)
at the interest rate 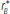 , as required by Equation
(29). The quantity of CLF rights purchased from the standing facility in equilibrium
is equal to the difference between the demand for
B +
F (the dark blue curve in Figure 7) and the supply of
B
(the light blue curve) at the interest rate
, as required by Equation
(29). The quantity of CLF rights purchased from the standing facility in equilibrium
is equal to the difference between the demand for
B +
F (the dark blue curve in Figure 7) and the supply of
B
(the light blue curve) at the interest rate
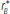 .
.
Several interesting results can be seen in Figure 7. First, setting the CLF fee allows
the central bank to control the regulatory liquidity premium directly, regardless
of the bond supply function μ. Even if the function
μ were changing over time or unknown to the central bank, the chosen
value of
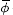 would always determine this premium
as shown in Equation (31). Second, Figure 7 shows there is a crowding out effect:
when
would always determine this premium
as shown in Equation (31). Second, Figure 7 shows there is a crowding out effect:
when
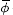 is set lower, banks purchase more CLF
rights but hold fewer bonds. The size of this effect is determined by the shape
of the bond supply function μ. In regions where the supply of bonds
is relatively elastic (i.e. the light blue curve is relatively flat), a small
decrease in
is set lower, banks purchase more CLF
rights but hold fewer bonds. The size of this effect is determined by the shape
of the bond supply function μ. In regions where the supply of bonds
is relatively elastic (i.e. the light blue curve is relatively flat), a small
decrease in
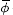 will lead to a large decrease in B*.
Conversely, in regions where bond supply is inelastic, the crowding out effect
will be small. More generally, Figure 7 shows how the bond supply function
traces out the set of outcomes available to the central bank. Setting
will lead to a large decrease in B*.
Conversely, in regions where bond supply is inelastic, the crowding out effect
will be small. More generally, Figure 7 shows how the bond supply function
traces out the set of outcomes available to the central bank. Setting
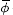 higher implies that banks will hold
more bonds in equilibrium, but the liquidity premium will also be larger. By
choosing
higher implies that banks will hold
more bonds in equilibrium, but the liquidity premium will also be larger. By
choosing
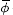 appropriately, the central bank can
pick out different points on this frontier, but the equilibrium pair (B*,
appropriately, the central bank can
pick out different points on this frontier, but the equilibrium pair (B*,
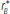 ) will always lie on the light blue
curve. In this way, choosing the CLF fee allows the central bank to determine
either the quantity of bonds held by banks or the equilibrium liquidity premium,
but not both.
) will always lie on the light blue
curve. In this way, choosing the CLF fee allows the central bank to determine
either the quantity of bonds held by banks or the equilibrium liquidity premium,
but not both.
5.4.2 A fixed-quantity auction facility
Now suppose the central bank chooses to sell a fixed quantity
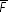 of CLF rights, possibly using an auction
format. Figure 8 illustrates the outcome under this approach. For any
of CLF rights, possibly using an auction
format. Figure 8 illustrates the outcome under this approach. For any
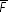 <θ
<θ
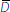 , Figure 8 shows that there is a unique
interest rate rB
such that the difference between the demand for bonds plus CLF rights (the dark blue
curve) and the supply of bonds (the light blue curve) is exactly
, Figure 8 shows that there is a unique
interest rate rB
such that the difference between the demand for bonds plus CLF rights (the dark blue
curve) and the supply of bonds (the light blue curve) is exactly
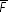 . The chosen quantity
. The chosen quantity
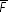 thus determines the equilibrium interest
rate on bonds
thus determines the equilibrium interest
rate on bonds
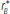 and the equilibrium quantity of bonds
B*. The equilibrium loan rate
and the equilibrium quantity of bonds
B*. The equilibrium loan rate 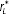 is determined by the
point on the red curve corresponding to the total quantity of bonds plus CLF
rights, B*+
is determined by the
point on the red curve corresponding to the total quantity of bonds plus CLF
rights, B*+
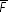 .
.
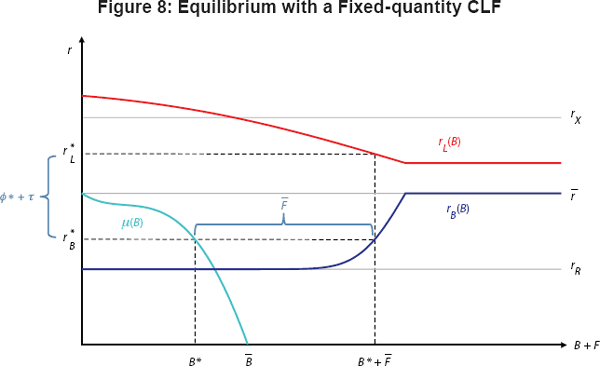
Comparing Figures 7 and 8, it is clear that the central bank in our model can achieve the same equilibrium outcome using either a fixed-price or a fixed-quantity CLF. In fact, this same outcome will obtain under any CLF pricing function φ that satisfies:
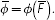
In reality, uncertainty about the positions of the (light blue) supply curve and
the (dark blue) demand curve are likely to play an important role in determining
the best design for the CLF. For example, the fixed-price design is likely
to be appealing to a central bank that wishes to stabilise the interest rate
spread
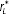 −
−
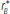 and let the quantity of CLF usage vary
depending on financial conditions. The fixed-quantity design, in contrast,
would be attractive to a central bank that prefers to keep CLF usage predictable
and allow interest rates to change in response to market conditions.
and let the quantity of CLF usage vary
depending on financial conditions. The fixed-quantity design, in contrast,
would be attractive to a central bank that prefers to keep CLF usage predictable
and allow interest rates to change in response to market conditions.
6. Pricing Committed Liquidity
Suppose a central bank has decided to create a CLF, which for ease of exposition
we assume to be operated as a fixed-price standing facility. How should the
price
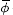 be set? One possibility is to aim to
replicate the equilibrium spread
be set? One possibility is to aim to
replicate the equilibrium spread 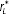 −
− 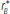 that would arise in
an economy where HQLA is plentiful and there is no CLF. In the context of our
model, this requires constructing a hypothetical supply function
that would arise in
an economy where HQLA is plentiful and there is no CLF. In the context of our
model, this requires constructing a hypothetical supply function
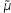 (B) that would apply if bonds
were plentiful in this economy. This function is represented by the dashed
light blue curve in Figure 9. The intersection of this hypothetical supply
function with the actual demand curve in dark blue determines the interest
rates (
(B) that would apply if bonds
were plentiful in this economy. This function is represented by the dashed
light blue curve in Figure 9. The intersection of this hypothetical supply
function with the actual demand curve in dark blue determines the interest
rates (
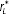 ,
,
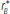 ) that would prevail in the hypothetical
situation. The central bank would then substitute these interest rates into
Equation (31) and set
) that would prevail in the hypothetical
situation. The central bank would then substitute these interest rates into
Equation (31) and set
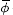 accordingly. As shown in Figure 9,
the actual bond supply function (in solid light blue) then determines the quantity
of bonds held by banks, B*, and the quantity of CLF rights purchased,
F*. One possible rationale for using this approach is that it equalises
the effect of liquidity regulation on interest rates across jurisdictions,
even when bond market conditions are very different.
accordingly. As shown in Figure 9,
the actual bond supply function (in solid light blue) then determines the quantity
of bonds held by banks, B*, and the quantity of CLF rights purchased,
F*. One possible rationale for using this approach is that it equalises
the effect of liquidity regulation on interest rates across jurisdictions,
even when bond market conditions are very different.
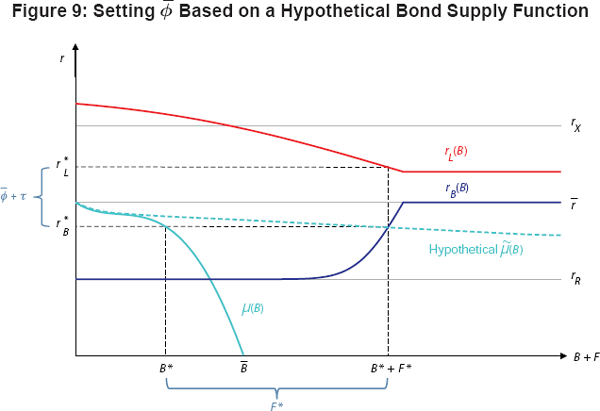
Notice, however, that the equilibrium allocations under the hypothetical supply curve
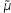 and the actual supply curve μ
are far from equivalent. In particular, banks' actual bond holdings B*
are much lower than they would be in the hypothetical situation, even though
interest rates are the same. To the extent that one goal of liquidity regulation
is to ensure that banks hold a more liquid portfolio of assets, it may be desirable
to set the CLF price higher than indicated in Figure 9, which would lead banks
to hold more bonds while increasing the interest rate spread
and the actual supply curve μ
are far from equivalent. In particular, banks' actual bond holdings B*
are much lower than they would be in the hypothetical situation, even though
interest rates are the same. To the extent that one goal of liquidity regulation
is to ensure that banks hold a more liquid portfolio of assets, it may be desirable
to set the CLF price higher than indicated in Figure 9, which would lead banks
to hold more bonds while increasing the interest rate spread
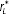 −
−
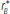 .
.
In general, the optimal pricing of the CLF is likely to depend critically on the
shape of the bond supply function μ, which traces out the trade-off the central bank faces between
two competing goals: encouraging banks to hold more bonds, and maintaining
spreads at reasonable levels. Figure 10 makes this point by assuming a very
particular shape for the function μ. If the central bank were to
follow the procedure described above of pricing the CLF according to the hypothetical
supply function
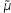 , the resulting equilibrium would have
banks holding a small quantity of bonds and meeting their LCR requirements
almost entirely through the purchase of CLF rights. However, the true bond
supply function μ is such that if the central bank were to increase
, the resulting equilibrium would have
banks holding a small quantity of bonds and meeting their LCR requirements
almost entirely through the purchase of CLF rights. However, the true bond
supply function μ is such that if the central bank were to increase
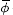 slightly, banks' bond holdings
would rise substantially and reliance on the CLF would diminish. In such a
situation, it seems likely that policymakers would prefer the latter outcome,
where the spread between
slightly, banks' bond holdings
would rise substantially and reliance on the CLF would diminish. In such a
situation, it seems likely that policymakers would prefer the latter outcome,
where the spread between
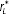 and
and
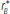 is slightly wider but banks hold a
substantially higher quantity of bonds.
is slightly wider but banks hold a
substantially higher quantity of bonds.
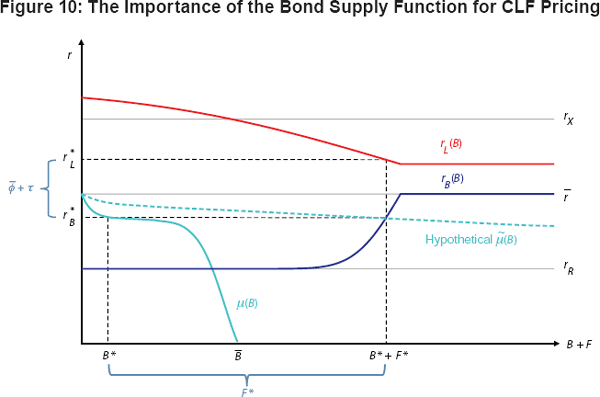
While the example in Figure 10 is in some ways extreme, it serves to make the general point that the optimal CLF pricing policy is likely to depend on the bond market conditions within each jurisdiction. In particular, policymakers will need to balance the costs associated with higher spreads against the benefits of having more liquid assets in the banking system. Doing so requires knowledge of how equilibrium interest rates and quantities respond to changes in the CLF pricing structure – that is, knowledge of the bond supply function μ. Estimating this relationship precisely is a difficult task, both ex ante and ex post. In light of this uncertainty, the RBA and SARB have taken pragmatic approaches in setting their CLF fees and both jurisdictions place a cap on the amount of CLF rights available to a bank (see Table 1). Moreover, the reasoning laid out here suggests that it may be desirable to take a flexible approach to CLF pricing, possibly adjusting terms as more experience is gained with this new policy tool.
7. Conclusion
We have presented a stylised model that can be used to analyse the economic effects of liquidity regulation in the form of an LCR requirement and a CLF. We have shown how the LCR requirement can have significant side effects in a jurisdiction with a limited supply of HQLA, leading to a large regulatory liquidity premium and pushing the short-term interest rate to the floor of the central bank's rate corridor. Introducing a CLF allows the central bank to mitigate these effects, regardless of whether it is organised as a fixed-price standing facility or using a fixed-quantity auction format. By pricing the CLF appropriately, the central bank can control either the equilibrium liquidity premium or the quantity of bonds held by banks, but not both. We argue that the optimal pricing arrangement will need to balance the costs of higher interest rate spreads against the benefits of having more liquid assets in the banking system. Our analysis has shown how the appropriate balance is likely to depend on local bond market conditions and thus may vary across jurisdictions. Moreover, the uncertainty about equilibrium relationships in the new regulatory environment means that central banks are likely to take a flexible approach to CLF pricing, adjusting terms over time as experience with these facilities increases.
While CLFs may not be immediately necessary in jurisdictions outside of Australia, South Africa, and a few others, it is possible they will prove to be a useful policy tool in other situations as well. Stein (2013) argues that a CLF may be beneficial even in jurisdictions where HQLA are plentiful because it allows the central bank to place an upper bound on the costs of liquidity regulation. In addition, as shown in our analysis above, the CLF allows regulation to focus more directly on prices whereas the LCR requirement is focused on quantities. Another possibility is that a CLF could be used as part of a central bank's regular procedures for implementing monetary policy and providing liquidity to the banking system. The Winters (2012) review of the Bank of England's operational framework, for example, suggests that selling CLF rights for an up-front fee, followed by a lower-than-usual interest rate on amounts drawn down, could potentially reduce stigma and other non-price barriers that limited the usefulness of existing facilities during the crisis. The model we present here could potentially be extended to address these issues, which represent an interesting area for future research.
Footnotes
The views expressed herein are those of the authors and do not necessarily reflect those of the Bank for International Settlements. [*]
The other options are using foreign currency HQLA to cover domestic currency liquidity needs and increasing the use of Level 2 assets with a higher haircut; see BCBS (2013). [1]
Our model is in the tradition of Poole (1968) and many others. Much of this literature focuses on interbank markets and the implementation of monetary policy through open market operations. Our focus here, in contrast, is on how banks' portfolio choices are affected by liquidity regulation. [2]
To simplify the presentation, we assume a bank always has sufficient collateral in the form of loans Li so that it can borrow as much as needed from the central bank to satisfy its regulatory requirements. [3]
The LCR rules assign a minimum run-off rate of either 3 per cent or 5 per cent to retail deposits covered by an effective deposit insurance scheme. Retail deposits deemed to be less stable are assigned a minimum run-off rate of 10 per cent; see BCBS (2013) for more detail. Secured transactions with the central bank are assigned a 0 per cent run-off rate. However, the LCR is a minimum standard; hence local authorities can set a higher value for these run-off rates at their discretion. See Bech and Keister (2013) for an analysis of the effects of an LCR requirement when loans from the central bank are assigned a positive run-off rate. [4]
The bonds in our model should, therefore, be interpreted as short-term bills. It would be straightforward to include long-term bonds that carry a term premium; what matters for our analysis is the spread between the interest rates on loans and bonds after accounting for risk and term premia. [5]
We do not explicitly model open market operations here, but any operations can be thought of as taking place in the market where bonds are bought and sold in Stage I of Figure 1. See Bech and Keister (2013) for a detailed study of the effects of open market operations in the presence of an LCR constraint. [6]
In general, bonds may yield a lower return than other risk-free assets because they provide additional, non-pecuniary services. These services can be especially valuable for non-bank entities, which cannot hold reserves and may value bonds for liquidity or hedging purposes, or for currency diversification. [7]
To simplify the presentation, we allow banks to short sell both loans and bonds and to run overdrafts in their reserve accounts in this stage, which implies there are no non-negativity constraints on this choice problem. In equilibrium, interest rates will be such that banks always choose to hold non-negative amounts of each asset. [8]
The result that banks hold zero bonds in this situation arises, in part, because we have assumed that banks receive no liquidity or other services from holdings bonds, whereas non-bank entities do. Alternatively, one could interpret B* as being banks' bond holdings beyond those used in its normal course of business, for example as collateral for settlement purposes. [9]
These results mirror those in Bech and Keister (2013), which shows how an LCR requirement tends to raise the interest rate on interbank loans with maturities outside the 30-day LCR window, while lowering the rate on shorter maturity loans. [10]
See Goodfriend (2002) and Keister, Martin and McAndrews (2008) for discussions of the floor system of monetary policy implementation. [11]
References
BCBS (Basel Committee on Banking Supervision) (2013), Basel III: The Liquidity Coverage Ratio and Liquidity Risk Monitoring Tools, Bank for International Settlements, Basel.
Bech ML and T Keister (2013), ‘Liquidity Regulation and the Implementation of Monetary Policy’, BIS Working Papers No 432.
Davis K (2011), ‘Basel III Liquidity Options’, Australian Centre for Financial Studies, Financial Regulation Discussion Paper Series 2011-02.
Debelle G (2011), ‘The Committed Liquidity Facility’, Address to the Australian Prudential Regulation Authority (APRA) and Financial Services Institute of Australia (FINSIA) Basel III Implementation Workshop, Sydney, 23 November.
Debelle G (2013), ‘The Impact of Payments System and Prudential Reforms on the RBA's Provision of Liquidity’, Address to the Australian Financial Markets Association (AFMA) and Reserve Bank of Australia (RBA) Briefing, Sydney, 16 August.
Goodfriend M (2002), ‘Interest on Reserves and Monetary Policy’, Federal Reserve Bank of New York Economic Policy Review, 8(1), pp 77–84.
Heath A and MJ Manning (2012), ‘Financial Regulation and Australian Dollar Liquid Assets’, RBA Bulletin, September, pp 43–52.
Keister T, A Martin and J McAndrews (2008), ‘Divorcing Money from Monetary Policy’, Federal Reserve Bank of New York Economic Policy Review, 14(2), pp 41–56.
Poole W (1968), ‘Commercial Bank Reserve Management in a Stochastic Model: Implications for Monetary Policy’, The Journal of Finance, 23(5), pp 769–791.
RBA (Reserve Bank of Australia) (2013), ‘Liquidity Facilities’, Technical Note for Domestic Market Operations, viewed 19 July 2013. Available at <http://www.rba.gov.au/mkt-operations/resources/tech-notes/liquidity-facilities.html>.
South African Reserve Bank (2012), ‘Provision of a Committed Liquidity Facility and Utilisation of Statutory Cash Reserves in Terms of the Basel III Liquidity Framework’, Guidance Note 5/2012.
Stein JC (2013), ‘Liquidity Regulation and Central Banking’, Closing Keynote to the Seventh Annual Credit Markets Symposium ‘Finding the Right Balance’, hosted by the Federal Reserve Bank of Richmond, Charlotte, 19 April.
Whitesell W (2006), ‘Interest Rate Corridors and Reserves,’ Journal of Monetary Economics, 53(6), pp 1177–1195.
Winters B (2012), ‘Review of the Bank of England's Framework for Providing Liquidity to the Banking System’, presented to the Court of the Bank of England. Available at <http://www.bankofengland.co.uk/publications/Documents/news/2012/cr2winters.pdf>.