RBA Annual Conference – 2006 Financial Innovation for an Ageing World Olivia S Mitchell, John Piggott, Michael Sherris and Shaun Yow[1]
Abstract
Over the last half-century, around the world, many nations have seen plummeting fertility rates and mounting life expectancies. These two factors are the engine behind unprecedented global ageing. In this paper, we explore how this demographic transition may influence financial markets and, in turn, how financial market innovation might help to resolve concerns flowing from global ageing trends. We first provide context by reviewing the economics, finance, and insurance-related literature on how global ageing patterns may influence capital markets. We then turn to insurance markets, and discuss a range of products and policies, including both retail and wholesale financial offerings for various forms of life annuities, long-term care benefits, reverse mortgages, securitisation of longevity risk, inflation-protected assets, reinsurance, guarantees, derivative contracts on residential property price indices, mortality swaps, and longevity derivative contracts. We also indicate how new public-private partnerships might be beneficial in enhancing the future environment for old-age risk management.
Introduction
Representing two-thirds of the world's population, and with its unique mix of systemically significant industrial and emerging market economies, the G-20 is a useful forum in which to develop a shared understanding of the implications of demographic change, and to consider responses to the associated economic and social challenges.
(G-20 2005, p 4)
Understanding how economies and financial markets will respond to global population ageing is an area of extraordinary policy and research interest. In recent years, substantial attention has been drawn to the macroeconomic implications of population ageing; thus after its 1997 Denver Summit, the BIS offered an extensive review of the impact of ageing on fiscal stability (G10 1998) and Davis (2004) addressed the implications of global ageing for financial and monetary stability. Recent high-level G-20 meetings, including this year's meetings in Australia, again underscore policy-makers' concerns at the highest level. The problem is simply put: over the past half-century, around the world, many nations have seen plummeting fertility rates and mounting life expectancies. These two factors are the engine behind unprecedented global ageing. In this paper, we explore how the demographic transition may influence financial markets and, in turn, how financial market innovation might help resolve concerns flowing from global ageing trends. We also indicate how new public-private partnerships might be beneficial in enhancing the future environment for old-age risk management.
Our approach is to assess what the economics, finance, and risk-management literature offers by way of insight, to help us evaluate how global ageing may spur demand for new financial products useful in helping to mitigate and insure against key old-age risks. We begin by providing an overview of relevant demographic trends and patterns of retirement wealth, and reviewing the literature on the effect of population ageing on capital markets and asset prices. We then turn to insurance issues, and point to the need for more complete insurance of risks which are disproportionately borne by the old, focusing especially on products associated with uncertain mortality and morbidity – longevity insurance, and insurance against long-term care costs. Along the way, we identify a range of products and policies that could be imagined to help manage these risks. For instance, these could include both retail and wholesale financial offerings for life annuities, long-term care benefits, reverse mortgages, inflation-protected assets, reinsurance, guarantees, derivative contracts on residential property price indices, mortality swaps, and securitisation of longevity risk. We also discuss ways in which public-private partnerships might be beneficial in enhancing the environment for old-age risk management, including ways in which national and international government organisations could help to identify, regulate, and possibly develop markets to finance these risks.
In what follows, we begin with a sketch of some relevant demographic trends and review what is known about the resources that older households take into retirement. Next we explore what is known about the impact of global ageing on asset markets. We then focus on the possible impacts of population ageing on insurance markets. Finally we discuss product developments in both the retail and institutional markets for longevity products.
1. The Ageing World
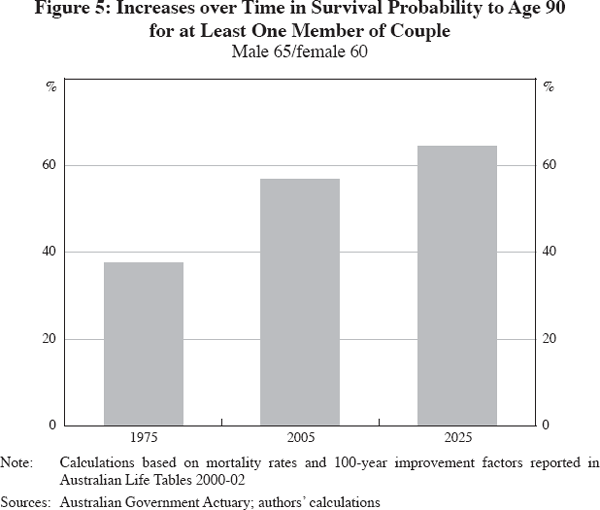
The reality of population ageing is now widely discussed, though the underlying dynamics are sometimes less clear. For this reason, we briefly review how population ageing is occurring. There are two main sources of this change: first, older cohorts of individuals are living longer than ever before in human history, and second, younger cohorts are having fewer children. An example offers a sense of the quantitative magnitude of the change in longevity. In 1975, there was a 38 per cent chance that at least one member of a married couple aged 65 and 60 would still be alive at age 90 (the age at which the female member would be now). For the same couple aged 65 and 60 in 2005, that probability is approximately 57 per cent. Further projections reveal that this last survivor probability increases significantly to 64 per cent in 2025 and 71 per cent in 2045.[2] Population ageing is already being experienced in many countries and this demographic transition is expected to become more pronounced over the next 40 years.
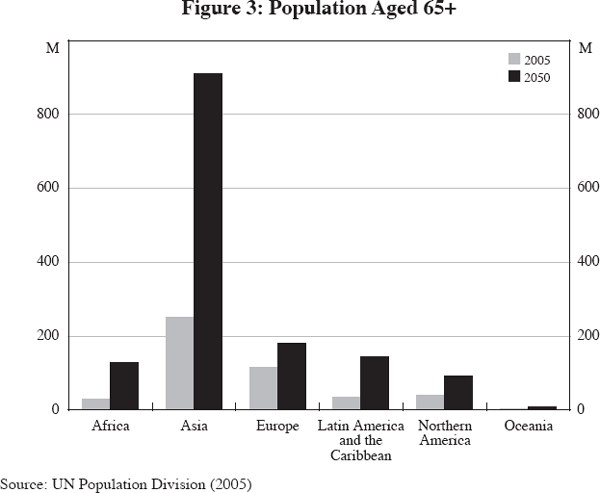
When these two effects interact with roughly constant retirement ages, the aged dependency ratio increases.[3] Of course, it is important to distinguish between increasing longevity and an increasing aged dependency ratio. The first gives a sense of the increase in aggregate size of the retired population; the second gives a sense of fiscal capacity to support the retired population (in the presence of constant retirement ages). It is also worth noting that these dynamics are occurring at different times and at different rates across countries and regions (Figures 1 and 2). Data on projected increases in the number of people aged over 65 by region show the most dramatic increase in Asia: by 2050, more than 910 million Asians will be older than 65, up from 250 million today. The fertility decline in China in the past 20 years has been very dramatic; Japan, the world's most rapidly ageing country, with low fertility and negligible immigration, faces far heavier aged dependency than Asia in general. On the other hand, Sweden enjoys fertility close to the replacement rate, while Spain's rate is one of the world's lowest. But the largest percentage increase in the aged dependency ratio occurs in Europe, due primarily to reduced fertility and not increased longevity.
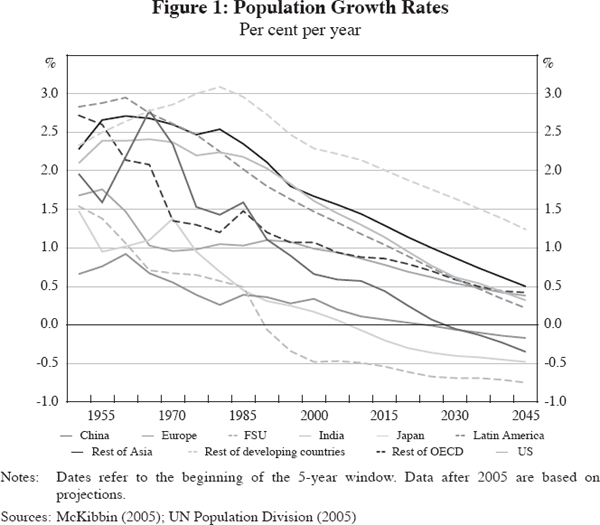
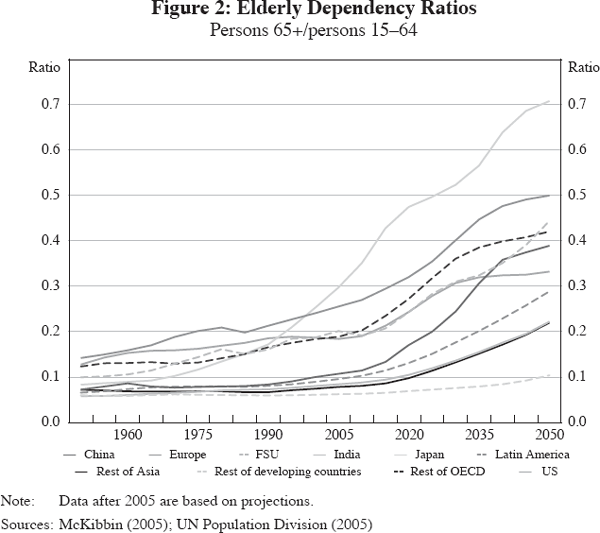
Generally, fertility differentials across countries are believed to be associated with differences in per capita wealth; differences in culture and attitudes; and differences in policies and infrastructure. Poor countries tend to have higher fertility than rich countries because children are seen as an investment, rather than requiring investment as in rich countries. Cultural differences are exemplified in the US, where the Hispanic population has a fertility rate of 2.5 children per woman, compared with a rate among Caucasians of 1.8 among women aged 40 to 44 in 2000 (Bachu and O'Connell 2001). And policy and infrastructure can lead to major differences – if women can return to work after having children without losing status or income, fertility tends to be higher. If countries mandate ceilings on the number of children, as with China's one child policy, then fertility falls dramatically. In addition, changes in fertility occur at different times. Japan is the world's most rapidly ageing country because the baby boom there ended in the early 1950s, whereas in most developed economies it continued until the early 60s. Similarly, the rate of increase in longevity is now far higher in Asia than in Europe and the US, where the benefits of good nutrition and health services are already reflected in current longevity patterns.
Because of these regional and national differentials in population ageing, there is reason to believe that the impact of ageing on financial markets may also occur at different rates over time (see Figure 3). Capital movements across national boundaries, and between regions, are likely to be partly demographically driven in the future, along with associated exchange rate adjustments. This generates opportunities for financial products which can to some extent facilitate these exchanges.
2. Ageing and Retirement Resources
In the developed world, most retirees rely heavily on public retirement benefits, loosely referred to here as social security benefits, funded corporate or state-run pensions, and owner-occupied housing. For this reason, understanding retirement resources and old-age financial vulnerability requires understanding older persons' rights to pensions and social security as well as home ownership patterns.
One way to see this is to examine US data, drawing on the most comprehensive survey of retirement wealth known as the Health and Retirement Study (HRS). Looking across a nationally representative sample of US households on the verge of retirement (age 51–61), researchers found that median retirement wealth was about US$340,000 (in 1992) while the average wealth stood at US$500,000 (Mitchell and Moore 1998; Moore and Mitchell 2000). Yet they also noted large differences across households, in that those in the 90–95 per cent ventile had 19 times the wealth of those in the 5–10 per cent ventile. Additional analysis explored the composition of retirement wealth, summarised in Figure 4. For the typical US household, financial assets comprise a relatively small portion of retirement wealth, whereas owner-occupied housing and funded pensions amount to 40 per cent of retirement wealth, and social security benefits constitute another 40 per cent of old-age consumption financing. This underscores the need for strong pension and social security systems, as well as the potential importance of a reverse mortgage market, in enhancing additional consumption for near-retirees and retirees of the future.
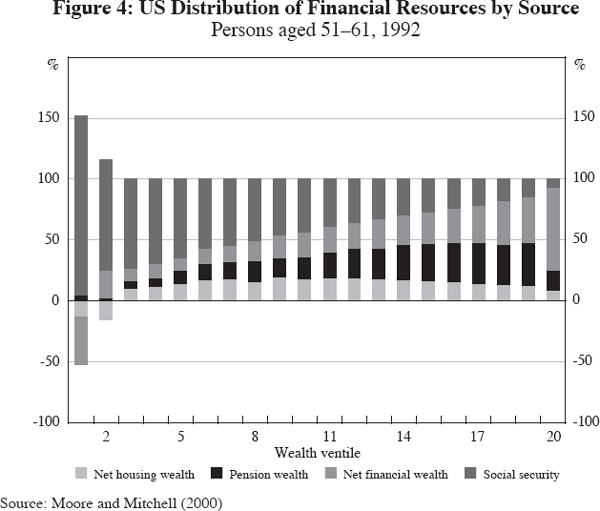
In other economies, government policies may differ regarding retirement support, and this in turn can influence the level, and composition, of retirement saving (see Tables 1 and 2). Results for New Zealand, for instance, show that housing wealth constitutes almost 30 per cent of retirees' assets, and government benefits almost 50 per cent. Very few in Europe hold any financial assets at all.[4]
| Total | Net housing | Pension | Net financial | Social security | |
|---|---|---|---|---|---|
| Per cent | |||||
| US | US$400K | 18 | 20 | 20 | 41 |
| NZ | NZ$454K | 29 | 0 | 14 | 48 |
|
Note: For US – household head aged 51–61 in 1992; for NZ – household head aged 45–55 in 2001 Sources: Moore and Mitchell (2000); Scobie and Gibson (2003) |
|||||
| Japan | Europe | US | |
|---|---|---|---|
| Financial wealth per household (€) | 180,967 | 119,985 | 270,986 |
| Financial wealth as a percentage of disposable income | 439.0 | 338.0 | 405.0 |
| Financial liabilities as a percentage of disposable income | 99.9 | 86.5 | 89.8 |
| Retirement wealth – pensions and social security (per cent)(a) | 73.0 | 133.0 | 45.0 |
| Residential property as a percentage of financial wealth | 67.0 | 87.8 | 38.3 |
|
Notes: Price conversion at purchasing power parity, end 2002 Source: Babeau and Sbano (2003), Tables 3, 4, 28 and 38 |
|||
Another interesting contrast is presented by Australia, one of the few OECD countries to have introduced a mandatory-funded defined contribution pension system. This is known as the Superannuation Guarantee Scheme, and it involves a mandatory contribution by workers of 9 per cent of their pay toward a funded pension each year. These benefits can be accessed between ages 55 and 60 depending on the date of birth. In addition, elderly who are poor are entitled to a means-tested benefit called the age pension, available from age 65, set at 25 per cent (40 per cent) of average male full-time earnings for singles (couples). As the age pension is an entitlement, independent of work history, the fact that it is means-tested on both assets and income means that over 80 per cent of those aged over 65 receive some amount of age pension. Because the Australian Superannuation Guarantee Scheme is still relatively young, accumulations are still low for many, and naturally they are much lower for those currently retired than for those still working. An average super plan balance for those aged 50–69 is A$83,000, while for retirees in their early 60s, the balance is A$68,000. Similar to the US, owner-occupied homes are also a key retiree asset, with average home equity values for those aged 50–69 worth A$223,000 in 2001.[5]
3. Population Ageing and Capital Markets
Predicting how population ageing might influence capital markets in the future, and retirement risk, might be expected to map fairly directly from life-cycle patterns of wealth accumulation and decumulation. That is, economists are fond of noting that the theory of life-cycle saving postulates that individuals save during their working lives so they can draw down this wealth in retirement. This approach might be thought to imply that population ageing will result in asset sales by the elderly, raising the supply of stocks and bonds relative to demand. Accordingly, some pundits have concluded that as populations age, the new waves of retirees will cause a ‘market meltdown’. In particular, this term has been defined as a sharp decline in asset prices expected when ageing baby boomers (persons born from about 1946–1964) sell off their assets to pay for retirement consumption. On the other hand, other commentators suggest that inasmuch as capital markets are global, demand for assets from emerging economies (some of which are experiencing slower (or no) population ageing) may help offset sales of assets by economies with older populations.
In this section, we seek to assess the importance of such effects by drawing on theoretical and empirical literature in the economics and finance fields. While theoretical studies tend to be fairly inconclusive, and the empirical research linking changes in demographic structure to capital market performance is contradictory, we believe that the weight of the evidence suggests there will be no great impact on financial markets of baby boomers ageing. That is, international stock and bond markets appear to have already incorporated existing information regarding population ageing. Accordingly, unless there were some dramatic and unexpected shift in demographics beyond that which is currently predicted, continued population ageing is unlikely to have dramatic effects on global capital markets. There could, however, be local effects, to be discussed below.
3.1 Theoretical analysis of ageing and capital markets
A simple yet useful theoretical model linking capital prices and population age structure is developed by Poterba (2001). He posits two hypothetical groups of people, young and retired. The young workers (of whom there are Ny) work and earn a normalised wage of 1 per period; they also save at rate s. The supply of capital is given (exogenously) by K, and the price of a unit of capital p will adjust to satisfy demand, in equilibrium:
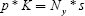
Accordingly, when the number of young workers rises, the price of capital will rise. By contrast, when a ‘pure’ baby boom occurs, a large birth cohort is then followed by a much smaller cohort. In this framework, asset prices will rise when the large cohort is of working age, and fall when it retires. Though the predictions from the model are consistent with an ‘asset-price meltdown’, Poterba points out that the formulation does not take into account several important real-world conditions. These include heterogeneous saving rates across different groups of people, the fact that capital is not fixed in supply, the fact that there are capital flows between open economies, and other possible effects of population ageing such as productivity changes, which could override the depressing demographic effects on asset returns.
A more sophisticated theoretical framework designed to address some of these issues is provided by Abel (2001). His view is that, even if asset demand does not decline in old age, the price of capital may still fall because of changes in the supply of capital. He therefore constructs a two-period overlapping generations (OLG) model that includes both variable capital supply and a bequest motive. This formulation relates the supply of capital to the price of capital in the previous period, and workers gain utility from leaving bequests to their children. This model implies that the dynamic behaviour of the price of capital follows a stationary autoregressive (AR-1) process, assuming the price of capital has a long-run unconditional mean. His simulation of the impact of the US baby boom then produces a short-term increase in the price of capital, followed by a reversion of capital prices to their long-run unconditional means. Abel further concludes that the presence of a bequest motive does not prevent the fall in capital prices when a variable supply of capital is introduced.
A more elaborate OLG approach is developed by Brooks (2002), who uses a four-period model to determine the quantitative impact of the US baby boomers on stock and bond returns. His important innovation is to assume that agents can shift their asset holdings from stocks to bonds as they age: this reflects the view that retirees face more consumption risk than workers, and since the return to capital is more volatile than to bond returns, they prefer to hold the risk-free asset. His model has a Cobb-Douglas production function. He simulates changes in population size of the magnitude of the US baby boom. As a large cohort lends to a small cohort of borrowers as baby boomers retire, the capital-labour ratio is then driven up 15 per cent above equilibrium by 2020, pushing returns down. Brooks' results suggest a fall in stock and bond returns of 92 and 82 basis points respectively (over 2000–2020). The model also predicts that baby boomers will earn 100 basis points less than previous smaller generations, over their lifetimes.
An even more complex OLG model is derived by Geanakoplos, Magill and Quinzii (2004). This formulation includes variable capital supply, bequests, dependency by both the young and retirees, and a tax-financed pay-as-you-go (PAYG) social security system. The authors note that the US stock market experienced a bull market (1945–1964) followed by a bear market in the 1970s, and a bull market in the late 1980s and early 1990s. They also point out that three 20-year periods coincide with alternating periods of low and high birth rates: the Great Depression, the baby boom of the 1950s, and the ‘baby bust’ of the 1970s. Accordingly, they model a world in which agents live for three periods (young, middle-aged, and retired); along the way they can invest in equity and bonds and they seek to maximise utility over their lifetimes. When small cohorts are middle-aged, equity prices are low. By contrast, when a large cohort becomes middle-aged, it bids up equity prices to double the original level, and later equity prices fall as workers retire and sell equity to a smaller cohort of young investors. The authors label this as the ‘favoured cohort effect’, where small cohorts do better than large cohorts in terms of lifetime consumption streams. The inclusion of a bequest motive with a variable supply of capital somewhat mitigates, but does not fully attenuate, the decline in equity prices when the large cohort reaches retirement (a similar result to Abel 2001). The authors also argue that the actual amplitude of the cycle in equity prices (for the period 1965–2004) is twice as large as can be explained by demographic cycles, with other explanations including oil shocks.
The models surveyed to this point take a ‘closed economy’ perspective, whereas Brooks (2003, this volume) focuses on a multi-regional approach. His OLG models simulate the effects of population ageing in an international context, assuming free international capital flows drive equalisation of capital returns across countries. His results suggest that, when a population ages, savings will come to exceed investment and produce a decline in capital returns. Consequently a region with an ageing population will become a capital exporter to regions with younger demographic structures and higher returns to capital. Open economies with international capital flows will therefore experience less of a fall in capital returns as a result of an ageing population. In practice, this means that the rapidly ageing European Union and US will become capital exporters to developing countries such as Latin America and Africa, until around 2020. Beyond that, baby boomers drawing down their wealth will produce large current account deficits in the European Union and the US, which must be financed by capital inflows from emerging economies such as Latin America. Africa will continue to be a capital importer due to its high population growth, while Japan will continue to be a capital exporter till 2040 due to its rapid population ageing.
Siegel (2005), like Brooks (2003), agrees that international capital flows will attenuate the anticipated fall in stock market returns. Describing this as the ‘global solution’, he contends that ageing countries will sell off capital to developing countries in exchange for goods and services. Using UN population data, Siegel measures the burden of ageing populations according to the retirement age required to support retirees (under existing pay-as-you-go pension arrangements). He predicts that an increase in labour productivity in emerging economies of 6 per cent, by 2050, would be sufficient to allow retirement ages in ageing countries to rise only marginally, by 2 years (to 64). The alternative scenario, of no productivity growth, results in a need to raise retirement ages to 76 in the developed world. Other policies are also suggested, including higher taxation and easier immigration, but these seem to be politically delicate and possibly less effective suggestions. Higher taxes will discourage the small proportion of the working population just at the time when more labour is needed. The impact of immigration would probably not be of sufficient magnitude to offset the needed increase in retirement age. These findings are therefore similar to those of Geanakoplos et al (2004).
3.2 Empirical analysis of demographics and capital market outcomes
Several analysts have sought to measure the empirical effect of population ageing on capital market outcomes, though again mostly with US data. As there has been no previous demographic shift of the magnitude that the nations with older populations confront, it must be noted at the outset that predictions are ‘out of sample’ forecasts.
Two studies by Poterba (2001, 2004) analyse the empirical relationship between US population ageing, and prices and returns for US stocks, bonds, and Treasury bills. To explore age patterns of asset ownership, he uses the Survey of Consumer Finances (SCF), which is a periodic cross-section survey on US asset ownership. This approach allows the identification of both age and cohort effects on asset holdings by regressing the value of assets held by the ith individual at time t, Ait, on age AGEijt and cohort dummies COHORTit:
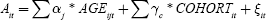
His results indicate that equity holdings do display an age pattern: they peak at US$32,500 for people aged 55–59 and then they fall to about US$25,000 by age 75. It is interesting that overall net financial assets show almost no decline in old age; thus holdings peak around ages 65–69 and remain fairly constantly at age 75+. On this basis, Poterba concludes that there will be no rush to sell financial assets as US baby boomers reach retirement. In other words, there will be no ‘asset-price meltdown’ in 2020–2030, as people will continue to hold considerable wealth up to the time of their deaths.
Poterba also links demographic measures to measures of the return to capital in regression models of the following sort for asset returns, Rt, and the aggregate price-dividend ratio (P/D)t:
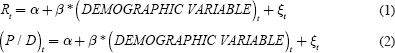
Several demographic variables are tested, including: the number of people over age 20; the percentage of the population between ages 40–64; and the ratio of people aged between 40–64 to the population over 20. The majority of demographic variables in Equation (1) show no evidence of correlation with any of the asset returns. In Equation (2), the price-dividend ratio is related to only a few of the demographic variables, and when the variables are differenced, the coefficients become statistically insignificant. Poterba also repeats the analysis for the United Kingdom and Canada, where results are similar: there is little evidence of a relationship between demographic variables and asset prices and returns.
Finally, Poterba develops a projected asset-demand variable constructed from SCF information which he also uses as an explanatory variable in the returns and price-dividends models:
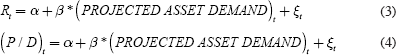
Only a weak link is seen between asset returns and projected asset demand. However, Equation (4) provides statistically significant results (albeit at only the 90 per cent confidence level). Poterba suggests that as baby boomers retire, asset prices will not decline because retirees in fact do not draw down all their wealth in old age.
An alternative empirical strategy is offered by Geanakoplos et al (2004) who construct a ‘MY ratio’ (the ratio of middle-aged to young persons) as a measure of demographic structure. This is linked to the price-earnings ratio PEt as follows:

Using US data, their results suggest that stock prices are positively correlated with the MY ratio: in fact, they predict that equity prices will decline until 2020, in line with the projected fall in the MY ratio. They also posit that returns on equity are influenced by capital gains or losses, which are in turn influenced by changes in equity prices. Therefore, they regress equity returns on the differenced MY ratio:

They find that the differenced MY ratio is positively correlated with equity returns, explaining 14 per cent of the variability. Also, the MY ratio is negatively correlated with equity risk premiums and uncorrelated with interest rates. The authors also consider international evidence, regressing stock market indices for France, Germany, Japan, and the UK (INDEXt) on the MY ratio in each country:

There is only weak international evidence of a similar relationship between the MY ratio and equity prices, as in the US, though Japan presents a stronger positive correlation between equity prices and the MY ratio. The inclusion of immigration in this model does not alter the MY ratio findings.
In sum, available evidence suggests that equity prices will fall to some degree as baby boomers approach retirement and sell assets to smaller ‘baby bust’ cohorts. On the other hand, bequests can attenuate this effect, and international capital flows will moderate them even more, particularly if developing countries with higher birth rates and younger population age structures can purchase assets from more rapidly ageing countries. Empirical studies are mainly limited to US data and tend to report only a modest inverse link between ageing and equity prices or returns.[6] Of course, it must be remembered that the empirical projections are fragile, given that the world has not yet experienced the consequences of such a dramatic change in the population age structure.
4. The Impact of Population Ageing on Housing Markets
Many analysts have sought to evaluate the possible implications of ageing populations on housing markets. Ageing is expected to have similar implications to those noted above for equity and bond prices: that is, if baby boomers sell their houses (‘downsize’) in retirement, this could trigger a substantial fall in house values. In what follows, we discuss what is known about the relationship between the population age structure and housing demand, the efficiency of the housing market, and housing prices.
Turning first to theoretical studies, the evidence indicates that population ageing can have a deeply depressing impact on housing prices if the housing market is inefficient. Mankiw and Weil (1989) model housing demand as a positive function of rental prices and the number of adults in the population of house-buying age. The authors simulate their model under two alternative conditions. The first assumes that investors have perfect foresight of the baby boom. In this case, the arbitrage equation suggests that expected capital gains on housing, P, will be the difference between the user cost of owner occupation rP and the rental price R(h):

In the second case, the arbitrage condition assumes that investors display myopic behaviour and believe the price of housing will remain the same in the following period. In other words, expected capital gains are zero:

In practice, the effect of a baby boom followed by a bust is simulated as a 2 per cent annual increase in the adult population from 1970–1979, falling to 1 per cent annually thereafter. Under the perfect foresight condition, the authors show that US housing prices would have been predicted to rise 3 per cent between 1969–1970, rise another 1 per cent between 1970–1975, and then fall back to original levels after 1975. If investors had perfect foresight, price changes would pre-empt the fall in housing demand as baby boomers age. Conversely, if investors display myopic behaviour, the simulation results would more closely match the actual US housing market experience. In particular, housing prices were slow to react to the baby boom news, and prices did not rise until 1970. Over the 1970–1980 period, housing prices grew by 14 per cent, twice as fast as what would have been expected under perfect foresight. Given that the second model tracks actual housing prices better, Mankiw and Weil conclude that the US housing market is inefficient.
4.1 Empirical evidence for the United States
Most statistical analysis of theoretical models of the effect of population change on house prices relies on US data. As noted earlier, Mankiw and Weil's (1989) work used US Census data 1970–1980 to track housing expenditures by age over time. The analysis regresses the value of the housing property on the individual households' age controls. They conclude that in the US, the ‘typical’ house-buying age is between ages 20–30, and demand declines by 1 per cent per year after age 40. The authors then take these estimated age-based housing demand coefficients (ai) and simulate changes in aggregate demand using Census population data for 1947–1987 using the following equation:

Demand Dt for housing at time t depends on the number of people aged i at that time, N(i,t), multiplied by the estimated age-demand coefficients ai. The results show that the emergence of the baby boom cohort is associated with substantial increases in aggregate housing demand during the 1970s, and the growth rate peaks at 1.66 per cent annually in 1980 when baby boomers are at their maximal house-buying age. Mankiw and Weil's forecasts suggest housing demand will then decline substantially from 1990 to 2010, with annual growth falling to only 0.6 per cent over this period.
One limitation of this model is the fact that it assumes that the age structure of housing demand remains constant over a very long period (1947–1987). Poterba (2001) tries to test for this using repeated cross-sections to construct the age structure of capital demand. The results indicate that the risk aversion of the representative consumer declines as the fraction of the population over 55 increases. Poterba concludes that it is difficult to find a significant relationship between housing demand and age structure for the US population over a 70-year period.
Green and Hendershott (1996) have an even more sophisticated approach, by using a hedonic pricing model to show how age, income and education affect demand for a constant quality house. Their age effects enter two ways, in both the total age derivative (where other variables are allowed to vary), and the partial age derivative (where other variables are held constant). They find that lower levels of education and income explain the observed lower demand for housing among older age groups, and that demand for housing is not affected significantly by age, but it is influenced by education and income. Assuming that the baby bust generation will have higher levels of both education and income than the previous cohort, this is predicted to attenuate the age-driven decline in housing demand.
Using their estimate of age-based housing demand to construct aggregate housing demand, Mankiw and Weil (1989) analyse the relationship between ageing and housing prices in the following regression model:
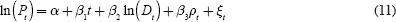
Here the dependent variable is the log of the price of housing Pt, housing demand is Dt, t is a time trend, and ρt is an error-correction term. Results indicate a strong positive correlation between the demand for housing and housing prices: that is, a 1 per cent increase in housing demand results in a 5.3 per cent increase in prices. The projected effect of the ageing of the baby boom generation is a 3 per cent annual decline in real housing prices, producing what became a notoriously large 47 per cent predicted fall by 2007 – a prediction that is now seen as unlikely to come true.
This extraordinarily large predicted effect of population ageing on future housing prices ignited a vigorous debate regarding its plausibility and robustness. Among the critics is Hendershott (1990), who questions the forecasting power of the model and the quality of the data. Using the same US Census data, Hendershott re-estimates the model using subsets of the data and then estimates in-sample forecasts (from 1970–1987). He reports that the forecasted values fit actual housing price trends badly (with an R-squared of 0.03) and argues that weak in-sample forecasting power undermines the credibility of the out-of-sample forecast. He then offers several additional regression equations which boost the model's explanatory power. One includes the real after-tax interest rate, RAT, which improves the fit of the model (with an R-squared value of 0.38). A different model allows for a shift in the constant and coefficient on the housing demand variable between the periods 1948–1969 and 1970–1987, and also includes gross national product GNPt, which enhances the R-squared to 0.69.[7]
Other studies have also added variables whose omission, they argue, biases estimated parameters. Holland (1991) includes the rent-price ratio R/P which then reduces the significance of housing demand in the housing price equation. Hamilton (1991) also posits that rental prices and housing prices should move in opposite directions, as renting and owner-occupation can be seen as substitutes. Therefore he prefers a different dependent housing price variable, namely the rental price component from US consumer price index (CPI) data, which he uses in a variant of Mankiw and Weil's Equation (11). Since all the coefficient estimates become insignificant, he concludes that this is proof of omitted variable bias. Hamilton and Hendershott also conclude that the negative coefficient on the time trend variable in the Mankiw and Weil regression is a model misspecification. The negative coefficient on the time trend variable forces the coefficient on the housing demand variable to be large and positive, simply to offset the negative time trend. Hendershott suggests that other factors should be controlled for, including labour force participation and productivity growth. Holland also shows that the earlier results are not robust since housing price and housing demand prove to be cointegrated.
4.2 Evidence for other countries
Relationships between population ageing and housing markets outside the US have also been studied. For instance, Engelhardt and Poterba (1991) adopt the Mankiw and Weil (1989) approach but use housing data from Statistics Canada. The researchers report that, though Canada and the US experienced similar population ageing, their housing market experience has differed sharply. Canadian housing prices rose rapidly in the 1970s and declined sharply in 1985; by contrast, US housing prices rose in the mid 1970s and declined little in the early 1980s. As a result, the coefficient on the housing demand variable is positive using US data and negative when using Canadian data. Engelhardt and Poterba conclude that movements in housing prices cannot be explained by demographic factors in the Canadian housing market.
Ageing's impact on the British housing market is taken up by Ermisch (1996), who uses cross-sectional data from the Joseph Rowntree Foundation Housing Finance Survey 1988–1989. Here HCi, the housing consumption variable, is measured as the value of the house purchased divided by a hedonic housing price index. Housing consumption is then regressed on the marginal cost of housing MCHi, current net household income Ii, housing structural variables Hi, and the age of the head of the household AGEi:
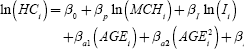
Ermisch models the underlying demand for owner occupation and the desire to move as part of a correction for sample selection bias. His results indicate two positive age effects on demand for housing. The ‘household formation’ effect is strongest among young workers with newly-purchased homes. The ‘household income’ effect is strongest among older individuals who have increased levels of wealth and consume higher-quality housing. The model suggests the formation effect is strongest, and it implies that population ageing will produce a projected halving in the growth of aggregate housing demand, from 0.65 per cent in the late 1980s to 0.35 per cent in 2000. The price and income elasticity of housing demand are estimated at −0.4 and 0.5 respectively. In other words, as baby boomers age, fewer new UK households will be formed, while the average amount spent on housing will increase. Though the author acknowledges the need to integrate housing supply as well, his study focuses mainly on the demand for housing.
To summarise, this literature suggests that housing prices are likely to decline somewhat as baby boomers reduce their housing demand. However, the impact will likely be far smaller than Mankiw and Weil's dramatic predicted drop of 47 per cent by 2007. Furthermore, there is reason to believe that the effect of ageing on housing prices could be neutral or even positive, if positive income and education effects on housing demand offset population ageing.
5. The Impact of Population Ageing on Insurance Markets
Global population ageing will also mean that more people are confronting longevity risk and health shocks. In turn, these facts raise questions about society's ability to sustain a rising and perhaps increasingly destitute share of very old retirees.
5.1 Longevity risk
This concern is focused on the worry that people may outlive their wealth, which can happen if they save too little, retire too early, and/or spend too quickly in retirement.
Systematic increases in longevity over time have been dramatic. There is a better-than-even chance that at least one partner in a conventional couple aged 65/60 today, will be alive at age 90. A generation ago, this probability was only a little better than one in three (see Figure 5).
The longevity problem has been exacerbated as firms and governments have phased out defined benefit (DB) pensions, and instead given increasing emphasis to defined contribution (DC) plans. This trend suggests that private insurance markets are likely to become increasingly important as populations age. Nevertheless, there is some consensus that annuity markets are not yet adept at helping individuals to manage longevity risk. In what follows, we discuss the risks faced by both providers and purchasers of insurance that may have contributed to longevity insurance market failure and review a range of possible solutions.
The traditional way to insure against outliving one's assets is to purchase an annuity, which is a financial product guaranteeing a lifelong stream of payments in exchange for an initial premium. Despite the initial appeal of annuity products, participation in such markets has been relatively thin in many countries, with the UK and the US being moderate exceptions. A possible explanation suggested by Brown et al (2001) is that people behave myopically and focus on the risk of dying too soon rather than the risk of living too long. Another explanation is that annuity prices may be too high due to adverse selection. This latter point is explored by McCarthy and Mitchell (2002) who measure adverse selection in annuity markets in Japan, the UK and the US by comparing mortality tables used in pricing annuity products against mortality tables from a baseline population. Their Actual/Expected (A/E) ratio is defined as:
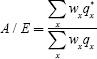
where 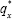 is the probability that an individual aged x
dies in the next year corresponding to the annuity mortality table, qx
is a similar probability of death corresponding to the baseline population
mortality table, and wx = (1–qx–1)wx–1
and weights are set so that w65 = 100.
is the probability that an individual aged x
dies in the next year corresponding to the annuity mortality table, qx
is a similar probability of death corresponding to the baseline population
mortality table, and wx = (1–qx–1)wx–1
and weights are set so that w65 = 100.
Their results show that adverse selection is strongest among voluntary annuitants in all countries. Male voluntary annuity purchasers display significantly lower mortality than the baseline population of the US male age 65 group: the A/E ratio is only 67.5 per cent in the UK, 65.3 per cent in the US, and 81.8 per cent in Japan. Female annuitants display 73 per cent of baseline mortality overall, with the exception of Japan where annuitants are found to have roughly the same mortality as the baseline population (though it appears this better result is a statistical fluke).
Various approaches have been tried to encourage retirees to spread their resources over their remaining life span. These can be thought of as products which provide some coverage against some retirement-related risks, while leaving some exposure to other risks. Table 3 provides a schematic representation of the relationship between different kinds of retirement products and insurance coverage for the major financial risks confronted by the retired. These include, besides longevity and inflation risk, investment risk (return and volatility), replacement risk (the risk that post-retirement income will not adequately replace wages) and annuity rate risk (the possibility that interest rate expectations change over time, so that the annuity price at the point of mandatory purchase will vary). This last risk poses a significant problem. The price of non-indexed annuities in particular can move significantly in quite short periods of time, since the nominal long-term rate of interest has much higher volatility than the real rate. This is especially true in countries with a high variance of inflation rates over time.
| Annuity type | Type of risk | ||||
|---|---|---|---|---|---|
| Longevity | Investment | Inflation | Replacement | Annuity rate | |
| Immediate term-certain fixed | Medium | High | Low | Low | Low |
| Immediate-life indexed | High | High | High | Medium | High |
| Pooled fund | High | High | Medium | Low | Low |
| Phased withdrawal | Medium | Low | Medium | High | Medium |
|
Source: authors' calculations |
|||||
The first two annuity products identified in Table 3 are well known. The third, a pooled annuity fund, is a device which allows the separation of idiosyncratic from systematic longevity risk. Since annuitants are predominantly concerned with idiosyncratic risk, while insurers are concerned with systematic risk, a product which separates these risks has potential appeal, in that it becomes possible to direct risk to stakeholders in the contract for whom the risk is less costly. The division is achieved through mechanisms which adjust the annuity payout in light of evolving mortality experience.
Another product which may be unfamiliar to some is a phased withdrawal plan, which provides coverage for a specified period, usually life expectancy, along with higher returns (and a standard annuity) and some exposure to investment risk. Phased withdrawals are popular in some emerging economies; they are also popular in Australia, where mandatory DC plans provide an accumulation at retirement for investment (Dus, Maurer and Mitchell 2005). Also, it would be possible, and in some cases desirable, to have financial products that would combine a phased withdrawal with a deferred annuity (Horneff et al 2006). These would provide financial insurance for later life, in exchange for a relatively modest sum at retirement. While such a combination has much to commend it, we are unaware of it on offer in the marketplace. Nevertheless, these new product designs may well have a future market, as the need for longevity insurance becomes clearer to consumers, governments and industry.
Friedberg and Webb (2006) adopt a simulation approach to quantify the aggregate mortality risk faced by an annuity provider. Using a Lee-Carter model to forecast mortality trends, they find annuities contribute significantly to the risk of insolvency. For example, an insurer selling joint life and survivor annuities to couples can reduce its probability of insolvency from 5 per cent to 1 per cent by increasing premium loadings from 3.78 per cent to 5.37 per cent. These results suggest there is a clear need for improvements in the way that insurers manage mortality risk.
It has often been suggested by actuarial theorists that life insurance and annuity products could be perfect hedges for each other: that is, life insurance which covers death could be used to hedge the longevity risks associated with offering annuity products to people who live too long (McCarthy and Mitchell, forthcoming). Yet in practice, adverse selection means that the mortality risks are not the same for both life insurance and annuity purchases, which limits the feasibility of natural hedging. Cox and Lin (2004) evaluate the possibility for natural hedging of life and annuity mortality risks by regressing the price of annuities, PRICE, on the extent of natural hedging within the company. Here RATIO is the log of the ratio of annuity reserves to total life and annuity reserves:
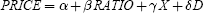
where X is a vector of control variables, and D is a vector of year effects. The authors conclude that insurance companies who offer both life insurance and annuity products can benefit somewhat from natural hedging. Accordingly, a benchmark insurer with 95 per cent of its business in life insurance and 5 per cent in annuity products, would pay out US$765 per month on its single-premium immediate annuity (sold to a 65-year-old male with US$100,000 to invest). By contrast, a company which took full advantage of natural hedging with a RATIO of 50 per cent could afford to increase monthly payouts by US$24 to US$789. Insurers who take advantage of natural hedging will be more competitive in annuity markets.
In practice, of course, it may not be possible for insurers to frequently alter their portfolios to fully realise the benefits of natural hedging. Instead, Cox and Lin (2004) propose mortality swaps as a way to achieve dynamic natural hedging. Assuming no counterparty risk, the mortality swap proposed takes place between a life insurer and an annuity provider. After agreeing that the present value of future cash flows are equal for the two products, the annuity provider will pay a floating benefit based on the number of deaths incurred by the life insurer in exchange for the premiums of the surviving cohort. These payments will be paid to an intermediary who facilitates the arrangement and only net payments need to be transacted. The authors suggest a forward-pricing model to determine the corresponding payments implied by the mortality swap. To account for adverse selection, Cox and Lin use a stochastic transformation to account for the risks of mortality improvement once a given mortality table is used in pricing annuities. The result is that, for every life insurance contract with a face value of US$1 million, the mortality swap can be made for annuity payments of US$267 for males and US$195 for females. Of course the market for mortality swaps is currently underdeveloped, requiring further innovation and research to help facilitate and price such contracts.
Other ways to help annuity providers manage longevity risks include the use of survivor bonds (also referred to as longevity bonds), as suggested by Blake and Burrows (2001) and Friedberg and Webb (2006). Payouts on these bonds increase as mortality improves, where mortality is measured by some pre-specified systematic mortality index. These authors contend that the absence of an instrument to help hedge against longevity risk is a key reason for underdeveloped annuity markets. To illustrate the significance of longevity risk on annuity products, they present a simple annuity-pricing model that relates the price P to mortality improvements through the adjustment factor fx, as follows:
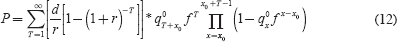
where d is the coupon rate, r is the discount rate, 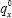 is the unadjusted mortality rate, and x0
is the age of the person when buying the annuity. Equation (12) shows that errors
in estimating future mortality trends, f x, will
complicate the appropriate pricing of annuity products. MacDonald (1997) shows
that assuming an adjustment factor of 0.8, forecast errors for mortality rates
of 65-year-old males are 10 per cent over a 10-year period. So for a male aged
65, the probability of surviving to age 85 ranges from 0.337 to 0.438, and
for survival to age 95, probabilities range from 0.053 to 0.153. The result
is that insurance companies price these mortality risks into cost loadings
and consequently offer annuity rates that appear expensive.
is the unadjusted mortality rate, and x0
is the age of the person when buying the annuity. Equation (12) shows that errors
in estimating future mortality trends, f x, will
complicate the appropriate pricing of annuity products. MacDonald (1997) shows
that assuming an adjustment factor of 0.8, forecast errors for mortality rates
of 65-year-old males are 10 per cent over a 10-year period. So for a male aged
65, the probability of surviving to age 85 ranges from 0.337 to 0.438, and
for survival to age 95, probabilities range from 0.053 to 0.153. The result
is that insurance companies price these mortality risks into cost loadings
and consequently offer annuity rates that appear expensive.
The survivor bond proposed by Blake and Burrows would allow insurers to hedge aggregate mortality risks. They are structured so that future coupon payments depend on the share of the whole population of retirement age, in the year of the issue of the annuity, who survive to the date of payment. Blake and Burrows also suggest a role for the government, which would be able to issue these bonds at the lowest price by spreading aggregate risk across the population. Survivor bonds would be useful in lowering the price of privately-sold annuities and facilitate the transition from public to private pension systems. One shortcoming of the plan is that existing tax systems do not spread tax burdens equally among households, so if the purchasers of annuities were mainly rich households, then the poor would effectively be subsidising the retirement of the wealthy. Another concern is that survivor bonds are not currently available on a large scale, so that techniques for designing appropriate hedges are underdeveloped.
Supply-side problems of adverse selection are the focus of Creighton et al (2005) who show that this phenomenon results in annuitants receiving only 80 cents per dollar of annuity product purchased. They propose as a solution, the establishment of a pooled annuity fund (termed Group Self-Annuitisation or GSA), where benefits each period are contingent on the number of people remaining in the insured cohort. The authors develop a case where annuity benefits, yt, defined as:
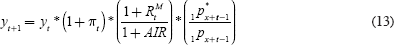
are related to inflation πt, and a mortality experience adjustment (which arises
from the difference between expected returns and mortality 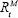 and
and 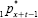 , and actual returns and mortality AIR
and 1px+t–1). The notion of the
GSA is to share the benefits and costs of longevity changes among surviving
group members: explicitly, individual annuitants bear cohort risk, while insurers
take on idiosyncratic risk. In this way, longevity risk is shared between both
the insurer and the insured, helping insurers to manage longevity risk and
thus offer products at lower prices.
, and actual returns and mortality AIR
and 1px+t–1). The notion of the
GSA is to share the benefits and costs of longevity changes among surviving
group members: explicitly, individual annuitants bear cohort risk, while insurers
take on idiosyncratic risk. In this way, longevity risk is shared between both
the insurer and the insured, helping insurers to manage longevity risk and
thus offer products at lower prices.
5.2 Protecting against health shocks
In view of the catastrophic nature of nursing home or long-term care (LTC) costs, it is surprising to many that the private insurance market plays such a small role in covering these risks. For instance, Garber (1996) argues that the ‘most striking feature’ of the US health care system is its failure to develop much of a private LTC insurance sector. Only one in five married couples deemed to be able to afford private LTC insurance in the US is adequately protected against this risk in retirement (Merlis 2003). Many attribute this shortcoming to the pervasive influence of public programs such as Medicare and Medicaid, which tend to crowd out privately-provided LTC insurance (Doerpinghaus and Gustavson 2002; Finkelstein and McGarry 2003). The wealthy tend to self-insure, leaving the middle-class as the group potentially most interested in private LTC coverage. It is widely believed, however, that this middle-group thinks that their LTC costs will be met through Medicare (which it does not), so hence do not purchase individual policies. Better marketing on the insurers' part could correct this misinformation, yet this has not yet gone very far.
Pauly (1990) highlights the appeal of LTC to elderly customers as being an important factor influencing demand. These customers prefer low-cost substitutes for LTC (provided as an institutionalised product). The medical literature provides contrasting conclusions, suggesting that home care is not an effective substitute for nursing home care. One well-designed experimental program in the US, known as the Channeling Demonstration project, showed that assigning expert case managers to help frail customers remain in the community increased costs and patient satisfaction, but did not forestall health deterioration, nursing home admission, or death (Garber 1996, p 148). Economic studies of individual preferences for quality reveals a lower price elasticity of demand the longer the length of the stay (Garber and MaCurdy 1990).
The Japanese LTC market, like the US, is characterised by significant growth although on a small scale. LTC contracts have more than doubled over 2000–03 (JILI 2003). Typical providers of LTC contracts include: private life insurance companies (for example, Nippon Life Insurance Company); private property and casualty insurance companies; the National Mutual Insurance Federation of Agricultural Cooperatives (Zenkyoren); and the Postal Life Insurance Service of the Japan Post system.
Several factors are likely to influence demand for LTC in future years. These include developments in health care and technology, and changes in the length of time during which the elderly population experiences periods of frailty. Their net impact on LTC demand is difficult to predict. Perhaps the greatest unknown is how attitudes will continue to evolve, given what is widely recognised as a fundamental change in society's approach to caring for the elderly. On the one hand, establishing an entitlement-oriented LTC program makes it possible for older persons to accept services without social stigma. On the other hand, demand for LTC may not grow as quickly as the elderly population. This is what has occurred in the US due to falling disability rates in the older population. Indeed, reduced elderly morbidity may mean that more people are able to care for their spouses in a non-market setting, thus reducing the demand for institutional LTC (Lakdawalla and Philipson 2002). In addition, levels of wealth will surely influence the demand for care, by directly shaping older consumers' ability to pay for care, and indirectly by influencing younger workers' ability to pay for rising premiums associated with any national mandatory system.
With regard to supply, one important aspect influencing private LTC costs is adverse selection. Garber (1996) suggests privatisation of underwriting reduces the costs of adverse selection, but it is important to note that the assessment technology remains in its infancy. Of course, mandating LTC coverage mitigates the problem of adverse selection in the purchase of the insurance, but it does not help in terms of service utilisation. Recent research by Finkelstein and McGarry (2003) finds no positive correlation between LTC insurance purchase and the probability of entering a nursing home. In fact, those who purchased LTC insurance in the US were more cautious and less likely to go into a nursing home, than those without coverage. This suggests that LTC insurance prices may not be unduly influenced by actuarially unfair selection, which eases the policy concerns about market failure.
There may also be other explanations for why insurers have only slowly moved into the LTC marketplace in the developed world. Uncertainty regarding the future paths of diseases, medical breakthroughs, and technological advances could dramatically change future life expectancies, years in frail condition, and consequently LTC costs. Also the mere existence of LTC insurance can potentially make it easier for families to ‘unload’ their relatives to nursing homes, which would fit with the concept of ‘social hospitalisation’ mentioned in the Japanese context above (Mitchell, Piggott and Shimizutani 2006). Both factors help to explain why private LTC policies in the US have had daily and lifetime (and sometimes financial) caps on coverage offered. In the past, many private policies did not guarantee renewability either, though this may be changing of late. And researchers have noted that private LTC policies are often not price-indexed, meaning that the consumer remains at risk for out-of-pocket expenses over the long term. Perhaps most importantly, private policies have tended to be silent regarding what they will pay if the government were to dramatically change its policies regarding medical care coverage, out-of-pocket requirements, spend-down policies, and the like. Such uncertainty on the consumer's part regarding the ultimate value of the private insurance surely serves to depress demand.
It is worth noting that government providers in other countries have often underestimated the demand for subsidised care when launching new long-term-care systems. For instance, Pratt (1999) points out that when the US Government established public support for LTC under the Medicare and Medicaid programs, it assumed that utilisation rates would continue at historical rates. In fact, demand proved to be far greater than anticipated. If rationing continues to be a problem, it seems that either the government will have to raise mandatory premiums or other taxes to pay for enhanced benefits, or the market for private LTC insurance will have to be opened up.
To this end, some have proposed the development of private LTC insurance policies sold through benefit plans offered by employers. In the past, US employers have exhibited little interest in subsidising this form of insurance directly (Wiener, Hixon Illston and Hanley 1994), but the 1996 Health Insurance Portability and Accountability Act (HIPAA) allows employer-paid premiums to be excluded from workers' salaries for tax purposes, and benefits are non-taxable up to a limit of actual LTC expenses (Rappaport and Stanger 1997). Additionally, US legislators have recently introduced bills to make LTC insurance premiums tax deductible to employees who purchase the private insurance via an employer-based flexible benefits or ‘cafeteria’ plan. These are plans where workers are granted a fixed dollar amount by their firms which they can then allocate across a range of benefit offerings. The proposed bill would grant a tax credit of US$3,000 per year to families who provide LTC services to relatives. Both provisions have an estimated revenue cost to the government of US$30 billion over the next decade (Rovner 2003). Whether that or another legislative initiative will pass is unclear, but it does seem that tax subsidies for LTC purchase are likely in the future.
Another approach that would use the workplace as a nexus for LTC provision would be to permit workers to use their mandatory LTC premiums to purchase private coverage, perhaps of a catastrophic-only sort. Contracting out in this fashion would give workers the responsibility of shopping around for LTC coverage, and it would also offer the advantage of lower costs and more competitive products for those of working age.
One concern with tax incentives for LTC is that they might be insufficient to induce low-wage workers to purchase enough LTC coverage. Nevertheless, rising costs of government-financed care have prompted a move to private market provision of care in several countries, including Australia, Germany, Sweden, and the UK (Go 2003). Though not-for-profit providers have traditionally dominated the market in Europe, LTC services are being increasingly provided by for-profit companies as in the UK and the US.
A proposal receiving attention in many ageing nations is to combine private LTC insurance with annuity products, which would potentially boost the market for both annuities and LTC cover. For instance, Warshawsky, Spillman and Murtaugh (2002) and Murtaugh, Spillman and Warshawsky (2001) propose an arrangement whereby a privately-sold life annuity product provides monthly payments that rise in the event that the insured party is certified as chronically and permanently disabled. The proposal's appeal is that the two-tiered coverage – longevity protection due to the annuity, plus a step-up in cash benefits if disabled – may attract more buyers than would a simple life annuity or a simple LTC scheme. This would be expected to reduce the potential for adverse selection which otherwise has been seen as a major obstacle to annuity sales (Brown et al 2001).
Alternative approaches include mandating that younger generations bear a larger share of LTC costs among the elderly. Lee (2003) reports China, New Zealand, and Singapore, have adopted this approach. Singapore has also bundled private insurance coverage with this scheme. In the extreme case of population ageing, as in Japan, Campbell and Ikegami (1998) suggest risk-pooling as a solution, requiring all workers to pay mandatory LTC premiums. This scheme places a burden on younger cohorts; for instance, US data reveal that 89 per cent of people aged 40–44 could meet LTC underwriting criteria, but only 68 per cent of those aged 70–74 are healthy enough to meet the screens (Merlis 2003).
The reverse mortgage (RM) market, about which we say more below, may offer an indirect method to fund LTC. Allowing elderly homeowners to borrow against owner-occupied housing, provides a means of utilising the full potential of an individual's retirement resources. There is evidence to suggest that a significant proportion of retirement wealth is tied up in owner-occupied homes, particularly in Japan where housing equity is 50 per cent larger than in the US.
6. Ageing and the Wealth Decumulation Process
As populations age, households will increasingly confront the challenge of having to manage their accumulated wealth during their golden years. This has been exacerbated by the global shift away from DB towards accumulation or DC pensions. So far, relatively few households have availed themselves of payout annuities, so the process of drawing down retiree wealth appears to be growing ever riskier. Several factors are worth mentioning in this regard, including the timing of annuitisation, reverse mortgages, and inflation risk.
6.1 Timing issues
Several recent papers have examined the question of what determines the optimal pattern of wealth management in retirement. Milevsky and Young (2001) show that delaying household annuitisation can benefit the elderly by exposing them to the chance of higher returns from investing in risky assets, so they can increase their wealth further before annuitising. For instance, a 60-year-old male annuitising immediately would have a rate of consumption of 8.34 per cent of his single premium. If the same person annuitised optimally at age 73, he could consume at a rate of 8.70 per cent of his principal prior to retirement and 11.24 per cent thereafter, assuming no adverse selection.[8] And even if the 60-year-old male had a hazard rate which was 60 per cent of the baseline population (that is, is less healthy), delaying annuitisation would still result in higher consumption when compared to annuitising immediately. This research implies that if retirees' subjective mortality expectations differ from the objective mortality tables used to price the annuity product, households will perceive a gain from delaying annuitisation, even if they are healthier than the baseline population.
So-called ‘self-annuitisation’ paths involving alternative phased withdrawal rules are the subject of research by Dus et al (2005). The retiree following this tactic continues to allocate his wealth across various investments and simply withdraws funds periodically for consumption. Compared to buying a life annuity, this strategy provides greater liquidity, the chance of higher consumption while alive, and the possibility of bequeathing some assets in the event of an early death. Of course, there is no pooling of longevity risk, so the retiree could outlive his assets. Such phased withdrawal approaches have grown popular following pension reforms in Europe and the Americas; for instance, in Germany, the government is seeking to boost asset accumulation for the ageing population by giving tax-preferred investment choices to individual-retirement accounts (IRA). After retirement, 30 per cent of the accumulated assets in the IRA may be taken in a lump sum but some of the rest must be used to purchase a deferred annuity payable from age 85. Similarly in the UK, personal pensions have had to be partly annuitised at age 75. The authors compare alternative approaches using explicit measures of risk and value along with a function reflecting the trade-off between these two, and they conclude that a phased withdrawal plan which minimises the risk of consuming less than a real annuity benchmark will require the retiree to allocate the majority of his retirement assets to fixed income. Of course, the specific asset allocation must vary as a function of plan design, age, and mortality risk, as well as preferences toward bequests. In more recent work, Horneff et al (2006) evaluate more complex strategies combining phased withdrawal and deferred annuitisation, and find that for all but the most risk averse, some amounts of phased withdrawals are appealing.
6.2 Investment guarantees
The emphasis on DC pension plans in the US public sector has led to some states offering government guarantees to transfer the investment risk from employees. Lachance, Mitchell and Smetters (2003) study the costs of one such guarantee offered by the public sector pension system of the State of Florida. This guarantee was in the form of a buy-back option, allowing workers to convert their DC pensions to a DB pension promise, as long as it was exercised before the termination of employment. The optimal time for an employee to exercise the buy-back option is then simulated, and the cost of the guarantee for the employer is as follows:
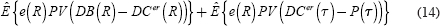
where DB(t) is the value of the DB plan at time t, DCer(t) is the value of employer contributions in the DC plan at time t, P(t) is the price of the buy-back option at the time of exercise, PV(.) is a present value function, e(R) is an indicator variable that takes the value of 1 when the option is exercised, and R is the number of years spent in the DC plan. The left-hand term in (14) is the cost the employer incurs at the termination of employment, when the employee converts from a DC plan to a DB plan, with the term DCer(R) representing the number of years the employee spends in the DC plan. The right hand term in (14) is the cost incurred by the employer at the time the option is exercised, denoted by τ.
The formula adopted by the State of Florida allows the DB benefits to be bought with the employee's accumulated benefit obligation. Under this formula, the cost of the guarantee could represent up to 100 per cent of the DC contributions if employees exercise the option optimally. Although such guarantees have the potential to manage the investment risk faced by employees, structuring them so that the burden is not significant remains an area for development (see Lachance and Mitchell 2003).
6.3 Reverse mortgages
Another possible approach would be to enhance the growth of reverse mortgages, as described by McCarthy, Mitchell and Piggott (2002) and Creighton et al (2005). In essence, reverse mortgages can help address the issue of households being ‘asset-rich but cash-poor’, as it permits retirees to borrow against their equity in their owner-occupied home without having to move out. The market potential has been estimated at 6.7 million households in the US, and 1.3 million households in Australia, and Mitchell and Piggott (2004) show that owner-occupation is highest among the age group over 60.
How these work is outlined in Figure 6. The owner's house price determines how much can be borrowed, and the loan value grows with interest over time. The figure indicates ‘crossover risk’, which is the risk to the lender that when the loan comes due, the property might be worth less than the loan. When the property growth rate is lower than the mortgage loan rate, at some point, the loan will ‘catch up’ to the property's sale price. In general, the point when the crossover occurs is a function of longevity, interest rates, general home appreciation, specific house appreciation/depreciation, and expenses.
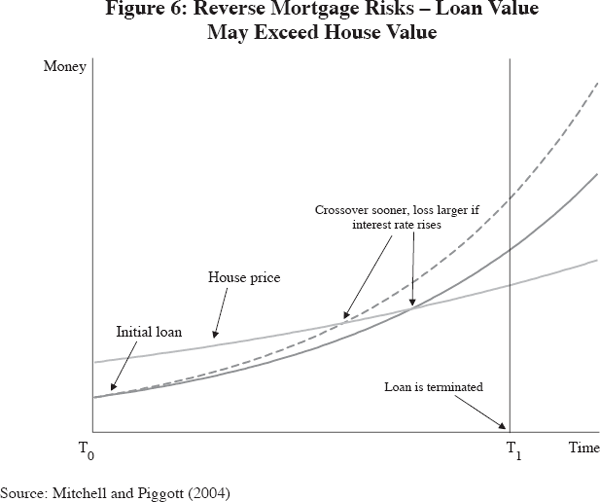
These risks have contributed to the slow growth of reverse mortgage markets, but their recent growth has been impressive. For instance, in the US, there were 40,000 reverse mortgage originations between 2001 and 2004, an increase of 500 per cent. Part of the motivation for the growth is support by the US Government in offering Home Equity Conversion Mortgages (HECM), which provide lenders with insurance against the depreciation of property values exceeding the value of the loan in the case of relatively low-wealth buyers. In Australia, various options can also be bundled with reverse mortgages: for instance, the Australian lending company, Bluestone, allows up to 20 per cent of the property's future value to be protected, permitting bequests to be made. Further, XCapital Health combines accommodation in a retirement home and health care with the reverse mortgage product. Securitisation of reverse mortgages would also help to encourage development of the reverse mortgage arena. Australian Seniors Finance has planned the country's first reverse mortgage securitisation for 2006. By allowing companies flexibility on the balance sheet, the market for reverse mortgages has strong potential for growth.
6.4 Inflation risk
Since retirees live for many years after leaving work, they face the real possibility that their assets will fail to keep track of inflation. Accordingly, Bodie (1988) has highlighted the introduction of consumer price index (CPI)-linked bonds as a key way that governments could offer a very valuable tool to help retirees hedge against inflation risk. His analysis indicates that CPI-linked bonds improve the efficient frontier marginally at the low- risk/return end, but they contribute substantial value as long-term hedges against inflation. There does appear to be a strong need for product innovation in the financial market for inflation-protected annuities, and Bodie argues that one such innovation would be an ‘inflation-proof retirement annuity’, backed by CPI-linked bonds. These bonds could also be used to index benefit promises in DB plans, which would attenuate the erosion of benefits indexed to nominal salaries and improve the DB plan portability.
Despite the attributes of CPI-linked bonds, and the fact that a few governments now issue them (including France, Israel, the UK and the US), it would appear that markets for these financial products are as yet thin. Governments have been slow to offer these products and insurers have not taken advantage of them during a period of quite low inflation. Perhaps inflation projections for the future will make them more attractive going forward.
7. Recent Product Market Developments
In recent years, products to manage longevity risk have been offered at both the retail and institutional levels.
7.1 Individual or retail products
In the retail marketplace, life insurance companies have started to issue products that provide for annuity payments specifying maximum annual withdrawal levels while guaranteeing capital maintenance, and deferred annuities with guaranteed annuity rates. These generally include an initial guaranteed maximum payment equal to a percentage of an asset base (such as the funds used to purchase the annuity). The asset base is then reduced by withdrawals in excess of the guaranteed maximum; it also grows over time if the assets perform well. The maximum percentages vary by age and are reported in Table 4 for one typical product.
| Age | Percentage |
|---|---|
| 55–59 | 4.0 |
| 60–64 | 4.5 |
| 65–69 | 5.0 |
| 70–74 | 5.5 |
| 75–79 | 6.0 |
| >80 | 6.5 |
| Note: authors' assessments of range of market products on offer | |
Payments continue throughout life even if the account balance falls to zero, thus providing protection for longevity. The charge for the longevity maximum guaranteed withdrawal for this product is 0.65 per cent per annum of the asset base for a single life and 0.8 per cent for joint lives. There are also investment charges based on daily net assets of 1.25 per cent as funds are invested into variable return investment portfolios. There is an option to annuitise the account balance into a fixed lifetime annuity. Withdrawals in excess of these maximums reduce the future guaranteed payments and are subject to withdrawal charges of up to 7 per cent. There is also a guaranteed minimum death benefit of contributions less withdrawals. The contract terminates at the annuitant's 95th birthday, at which time they must take a lump sum withdrawal or select an annuitisation option. The longevity protection in these products provides the maximum guaranteed withdrawal after the account falls to zero at around age 90, providing insurance for those surviving 25 years beyond the purchase date. An important factor causing the account balance to fall to zero after allowing for investment returns, given these maximum withdrawal percentages, is the impact of fees and charges.
In a typical deferred annuity product, the funds are invested to maturity and the product provides various annuity options, including a guaranteed minimum income benefit, a life annuity, a life annuity with period certain and with refund certain as well as variable annuity payout options. There is a charge for the guaranteed minimum income. The product often takes the form of a tax-preferred deferred annuity contract designed for the accumulation phase, but it may also include built-in annuity options on maturity. Guaranteed annuity purchase factors are included at the time an election to purchase an annuity is made. These factors are based on conservative actuarial factors and would normally be expected to be smaller than those under the standard annuity payout options. Money-back options in retail longevity products are also seen as an important component of product design.
Historically, annuity products have been thought of as expensive, though research by Brown et al (2001) and others shows that many annuities are actually quite fairly priced. The longevity guarantee in lifetime annuity products may also be costly depending on the investments allowed for the funds backing the annuity payments. In addition, more complex products include guarantees for death, withdrawal, and maturity benefits, all of which add additional costs. Over time, there has been increased competition in the US market, with a concomitant reduction in annuity expenses. For instance, the lowest fees reported on Morningstar/VARDS (on 31 December 2004) were 25 basis points per annum for variable annuity contracts, versus an industry average of 141 basis points. These fees would normally not include any charges for longevity and other guarantees, providing only an investment vehicle for tax-deferred retirement savings.
7.2 Institutional products
In recent years, annuity providers have strived to embed new investment choices in their products, linking returns to survival indices or cash flows from investment portfolios. In general, however, institutional products mainly provide coverage against adverse mortality events, but do not protect against cohort-wide mortality improvement. In a few circles a discussion has begun concerning the possibility of securitisation of mortality risk, thus gaining access to a larger pool of capital, and providing investors with returns from a risk that may be largely uncorrelated with other financial market returns. Issues in the design of these products are beginning to be addressed, including the development of a mortality index and the extension of securitisation techniques to include longevity risk. Thus far, the reinsurance market capacity for longevity risk is limited, so that it may make sense to turn to financial markets as an alternative source of institutional risk pooling.
Market responses to the need for these products has been mixed. For instance, Swiss Re has issued mortality-linked securities to manage adverse mortality risk, most recently with products known as Vita I and Vita II. In December 2003, a 3-year bond worth US$400 million was issued by Swiss Re and Vita Capital in the form of a floating rate bond linked to a mortality index. The repayment of principal was linked to a mortality index of experienced mortality rates in five countries (France, Italy, Switzerland, the UK, and the US). The spread was 135 basis points over LIBOR and the bond effectively covered catastrophic mortality risk such as an epidemic or perhaps a major terrorist attack or natural catastrophe. As another example, the first longevity bond was known as the EIB/BNP bond; in November 2004, BNP Paribas announced the issue of a longevity bond by the European Investment Bank (EIB) to hedge long-term systematic mortality risks. The payments on the latter bond were linked to a survivor index based on UK males aged 65. The total value of the issue was to be £540 million, and was primarily intended for purchase by UK pension funds. The issue was announced in November 2004 and withdrawn late 2005 without being issued, partly because of concerns with basis risk between the index and mortality risks in insurance and pension funds.
The contrasting market response to these two issues highlights the fact that the market for mortality-based institutional products is in the early stages of development and growing slowly. Developing the public market for mortality-based products is essential to accessing large capital markets. In doing so, these initiatives exploit the fact that financial market investors, in comparison to insurance markets, are more willing and capable of taking on these risks. Research into the pricing will help to develop a market for mortality-based products. Cox and Lin (2005) and Cairns, Blake and Dowd (2004) both deal with this issue. Many other mortality-based derivative contracts have been proposed or are under development. These include survivor bonds where coupon payments are linked to the number of survivors in a given cohort, survivor swaps where counterparties swap a fixed series of payments in return for a series of payments linked to the number of survivors in a given cohort, annuity futures where prices are linked to a specified future market annuity rate, and mortality options in the form of contracts with option characteristics whose payoff depends on an underlying mortality table. Comprehensive coverage of various examples and opportunities of the securitisation in life insurance is provided by Cowley and Cummins (2005).
An interesting development supporting the growth of these products is the recent launch of the Credit Suisse Longevity Index. It provides an objective mortality and longevity index for investors, insurance and reinsurance companies, pension plans, and other institutions exposed to longevity risk, permitting them to create new institutional financial products. Although basis risk remains an issue for insurers and pension plans, securities based on such an index to offset longevity risk have lower overall longevity risk. Institutional products to protect against longevity risk then can offer risk pricing and hedging, underpinning the increased issue of retail longevity insurance products. Products based on an index such as this could do a great deal to serve as the foundation for a more liquid market in longevity risk at the institutional level.
8. Political Risk and Demographic Ageing
Global population ageing is also putting severe pressures on traditional unfunded (PAYG) national pension systems around the world. Recent projections find that most of the OECD nations will have to cut retirement system benefits substantially and/or raise taxes dramatically, in order to keep these systems solvent. Many nations have already undergone so-called ‘parametric’ reforms, altering parameters such as tax rates, retirement ages, and benefit formulas to deal with cash-flow shortfalls. Going forward, legislating parametric changes is increasingly becoming politically divisive and infeasible. Accordingly, the huge underfunded liabilities of public pension and many retiree health care plans around the world presents an enormous source of political risk, attributable to and in turn affecting retirees in the baby boom generation and beyond.
In response to these challenges, some countries – most notably Chile – have moved to privatise a portion of their old-age income systems, as a means of curtailing perceived political risk. Of course this process has both positive and negative efficiency effects. Theory suggests that gains should result from lower effective tax rates on labour and positive effects on labour supply incentives. Furthermore, supplanting unfunded PAYG promises with funded capitalised accounts offers workers the chance to diversify their assets and reduce the risk of political confiscation. Nevertheless, public pensions can achieve redistributive objectives that may be difficult to obtain with private-funded vehicles. For instance, Nishiyama and Smetters (2005) simulate a multi-period OLG model in which heterogeneous agents face idiosyncratic earnings shocks and uncertain longevity. Gains or losses from privatisation are redistributed to future generations by the government. Their results suggest that privatisation produces some gains when wage shocks are insurable, but much smaller gains if wage shocks are uninsurable. Different scenarios are simulated, including allowing for international capital flows, private annuity markets, contribution matching, and progressive benefit formulas. In many cases, privatisation can result in efficiency losses. In other words, the benefits of improved labour supply incentives can be offset by the loss of risk-sharing under an unfunded social security program. It should be noted, however, that these conclusions do not generally take into account the costs of moving from an insolvent PAYG system to a solvent one.
A different tactic might be to figure out how to securitise future revenue flows promised under tax systems, which might reduce political risk. This idea is taken up by Valdés-Prieto (2005), who argues that a PAYG pension plan's assets consist mainly of the present value of all future taxes from the government to support plan participants. The ‘unfunded liability’ or PAYG asset is the source of political risk, as changes to legislation are often not timely nor sufficient to maintain the solvency of the pension fund. When pension system assets (if any) and PAYG flows are insufficient to cover liabilities, the difference is referred to as the implicit fiscal liability (IFL). The PAYG asset is based on the financial position of current members, while paying for the IFL relies on general taxpayers to ensure solvency. He argues that a pension plan is generally not empowered to collect transfers from the government; in this sense, these assets are not secured by property rights, but only the government's promise to donate future funds.
Valdés-Prieto then describes a complex securitisation process which would substitute the PAYG asset for a covered wage bill (CWB) perpetual bond. The first step requires identifying implicit taxes on future generations which subsidise current PAYG pension plan members. A law would then have to endow a pension institution to have property rights over the PAYG asset, and its strength would rely on the credibility of the government to remain fiscally responsible. CWB bonds can then be created based on the cash flows owed by plan members, not those owed by the state. Valdés-Prieto suggests that CWB bonds be issued such that dividend payouts are split into tranches (linked to the CPI or a wage index) to increase the attractiveness of the offer. The final step ensures the solvency of a pension plan and prevents the IFL appearing on the balance sheet. The presence of the IFL means that the pension plan is still subject to political risks. By adopting a set of rules for risk allocation, the plan must actively trade CWB bonds to ensure that they match their assets and liabilities.
Such a reform of an unfunded social security system would have some appeal, as it facilitates risk-sharing by making aggregate human capital tradable across generations which is not now feasible in existing capital markets. On the other hand, this framework would introduce significant moral hazard, reducing labour supply incentives and reducing reasons to participate in the plan. Adverse selection in household earnings reports will also be driven by the PAYG tax rate. And governments remain a source of political moral hazard, as changes to the tax rate and delaying the collection of taxes could be used to manipulate the price of CWB bonds. Nevertheless, this is a creative proposal that may be feasible at some national level, perhaps with the support of governments interested in creating national wage indices (Shiller 1998).
9. Conclusions and Discussion
This paper has reviewed the theoretical and empirical lessons regarding the potential impact of population ageing on global financial markets. Against this backdrop, we seek to draw conclusions about financial products such as longevity insurance and long-term care (LTC) insurance that might enhance old-age retirement risk management.
We acknowledge that the onset of massive demographic change may have some undesirable impacts on key forms of private and public old-age support. To respond to these shortcomings, we have outlined products that may not yet exist, or which exist but do not yet have much purchase, that can partially address these. In general, there are many products that could help allocate risk more efficiently across stakeholders. These could include reverse mortgages, annuities linked to LTC needs, survivor and mortality bonds, and mortality derivative securitisation. Yet financial and insurance markets thus far have been thin. This may be partly accounted for by myopia on the part of consumers, but is almost certainly partly due to supplier reluctance, based on uncertainties about future mortality trends, and more general information asymmetry in these insurance markets, leading to moral hazard and adverse selection against which it is difficult to price attractively. We therefore propose that the public sector in developed nations take a proactive stance to partner with private sector entities in the future, to generate better and more common information, and to help with better management of the risks associated with ageing. Important to this process will be new attention to relevant tax and regulatory reform (see also Groome, this volume).
Governments in many developed nations have taken substantial responsibility for youth and retirees in the past. Thus they provided education, invested in health care, developed the housing market, and built large social security systems. Looking forward, some of these trends will have to slow and even reverse, given rising budget deficits. Yet there are substantial opportunities for national, and indeed international, cooperation to solve market coordination problems.
It is worth considering in more detail the potential role of supra-national institutions in providing support for these markets and products, especially those concerned with longevity and LTC insurance, at both the institutional and retail levels. It would be entirely possible for the World Bank, for example, to issue survivor bonds, or to create some equivalent hedging instrument to allow annuity issuers to immunise their exposure to systematic mortality increases.
While annuity markets do exist in the UK and the US, in many smaller countries a competitive market for these products is not feasible. The possibility of a supra-national organisation overseeing a market in which annuities are issued globally on a franchise basis holds some appeal here. A suite of standard insurance products could be specified, and insurers could bid to provide them, possibly along the lines of a Demsetz auction. At the very least, such organisations could set up some consumer-friendly checklists for prospective buyers.
Such organisations are also well-placed to coordinate, with national government help, the development of accurate mortality tables for annuitants. National governments may well respond positively to an initiative whereby they require insurance companies to release their annuitant mortality experience, for example. This would help greatly in pricing longevity risk internationally. There are currently international guidelines for national account preparation; similarly, guidelines could be prepared for the computation of future mortality, social security liability, and related indices. Especially with respect to morbidity and the risk of requiring long-term care, a major international effort will likely be required to generate publicly available risk tables.
Once these activities are under way, creative new products may evolve, especially if market development is facilitated by government help. Sensible intervention in the near future, before the demographic transition progresses further, may pay off substantially in the form of better management of risks facing future retirees.
Footnotes
The authors express appreciation for research support to the Reserve Bank of Australia,
the Pension Research Council at The Wharton School, the Centre for Pensions
and Superannuation at the University of New South Wales, and the Economic
and Social Research Institute, Cabinet Office, Government of Japan. Christopher
Kent and Graydon Paulin provided useful comments. This research is part of
the NBER programs on ‘Aging’ and ‘Labor Studies’.
Opinions expressed herein are those of the authors alone, and not those of
any institution with which the authors are affiliated.
Olivia Mitchell is a Professor of Insurance & Risk Management at the
Department of Insurance and Risk Management, The Wharton School, University
of Pennsylvania (mitchelo@wharton.upenn.edu).
John Piggott is a Professor of Economics and Acting Dean at the Faculty of Commerce
and Economics, University of New South Wales (j.piggott@unsw.edu.au).
Michael Sherris is a Professor at the School of Actuarial Studies, Faculty
of Commerce and Economics, University of New South Wales (m.sherris@unsw.edu.au).
Shaun Yow is a Research Associate at the Centre for Pensions and Superannuation,
University of New South Wales (shaun.yow@student.unsw.edu.au).
[1]
These estimates are based on Australian longevity but may broadly be generalised across all developed economies. [2]
Indeed in many nations, the average age of retirement has actually declined, though this trend may now be flattening. [3]
These comparisons are for the whole population, not just the aged, but they nevertheless highlight the generous social security promises that have been made in many continental European economies. [4]
These values are for people who were working one year previously. The values represent about 95 per cent of gross home value – on average, mortgage debt was about 5 per cent of the value of the asset for this group. [5]
Davis (this volume) and Brooks (this volume) estimate similar models using international data and come to much the same conclusion. [6]
The extended model is expressed as:
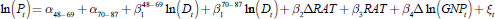 [7]
[7]
These estimates assume standard parameters for investment returns: non-annuitised funds are invested in a risky asset with drift 0.12 and volatility 0.20 and the rate of return on the riskless asset is 0.06. The individual has a coefficient of risk aversion of γ=2 (more risk adverse) and a subjective hazard rate in line with the mortality table used by the insurance company (average health). [8]
References
Abel AB (2001), ‘Will Bequests Attenuate the Predicted Meltdown in Stock Prices when Baby Boomers Retire?’, Review of Economics and Statistics, 83(4), pp 589–595.
Bachu A and M O'Connell (2001), ‘Fertility of American Women: June 2000’, U.S. Census Bureau Current Population Reports No P20-543RV.
Babeau A and T Sbano (2003), ‘Household Wealth in the National Accounts of Europe, the United States and Japan’, OECD Statistics Directorate Working Paper No 2003/2.
Blake D and W Burrows (2001), ‘Survivor Bonds: Helping to Hedge Mortality Risk’, The Journal of Risk and Insurance, 68(2), pp 339–348.
Bodie Z (1988), ‘Inflation, Index-Linked Bonds, and Asset Allocation’, NBER Working Paper No 2793.
Brooks R (2002), ‘Asset-Market Effects of the Baby Boom and Social-Security Reform’, American Economic Review, Papers and Proceedings, 92(2), pp 402–406.
Brooks R (2003), ‘Population Aging and Global Capital Flows in a Parallel Universe’, IMF Staff Papers, 50(2), pp 200–221.
Brown JR, OS Mitchell, JM Poterba and M Warshawsky (2001), The Role of Annuity Markets in Financing Retirement, MIT Press, Cambridge.
Cairns AJG, D Blake and K Dowd (2004), ‘Pricing Death: Frameworks for the Valuation and Securitization of Mortality Risk’, Center for Risk and Insurance Studies Working Paper.
Campbell JC and N Ikegami (1998), The Art of Balance in Health Policy: Maintaining Japan's Low-Cost, Egalitarian System, Cambridge University Press, Cambridge.
Cowley A and JD Cummins (2005), ‘Securitisation of Life Insurance Assets and Liabilities’, The Journal of Risk and Insurance, 72(2), pp 193–226.
Cox SH and Y Lin (2004), ‘Natural Hedging of Life and Annuity Mortality Risks’, Center for Risk Management Insurance Research Working Paper No 04-08.
Cox SH and Y Lin (2005), ‘Securitisation of Mortality Risks in Life Annuities’, Journal of Risk and Insurance, 72(2), pp 227–252.
Creighton A, H Jin, J Piggott and EA Valdez (2005), ‘Longevity Insurance: A Missing Market’, The Singapore Economic Review, 50, Special Issue 1, pp 417–435.
Davis EP (2004), ‘Demographic and Pension-System Challenges to Financial and Monetary Stability’, paper presented at the Austrian National Bank 32nd Economic Conference on ‘Growth and Stability in the EU’, Vienna, 27–28 May.
Doerpinghaus HI and SG Gustavson (2002), ‘Long-Term Care Insurance Purchase Patterns’, Risk Management and Insurance Review, 5(1), pp 31–43.
Dus I, R Maurer and OS Mitchell (2005), ‘Betting on Death and Capital Markets in Retirement: A Shortfall Risk Analysis of Life Annuities versus Phased Withdrawal Plans’, Financial Services Review, (14), pp 169–196.
Engelhardt GV and JM Poterba (1991), ‘House Prices and Demographic Change: Canadian Evidence’, Regional Science and Urban Economics, 21(4), pp 539–546.
Ermisch J (1996), ‘The Demand for Housing in Britain and Population Ageing: Micoreconomic Evidence’, Economica, 63(251), pp 383–404.
Finkelstein A and K McGarry (2003), ‘Private Information and its Effect on Market Equilibrium: New Evidence from Long-Term Care Insurance’, NBER Working Paper No 9957.
Friedberg L and A Webb (2006), ‘Life is Cheap: Using Mortality Bonds to Hedge Aggregate Mortality Risk’, NBER Working Paper No 11984.
G10 (1998), ‘The Macroeconomic and Financial Implications of Ageing Populations’, a report prepared in response to an initiative at the June 1997 Denver Summit.
G-20 (2005), ‘G-20 Workshop on Demographic Challenges and Migration’, Proceeding of the 27–28 August meeting, Commonwealth of Australia, Sydney. Available at <http://www.g20.org/Public/Publications/Pdf/2005_workshop_proceedings.pdf>.
Garber AM (1996), ‘To Comfort Always: The Prospects of Expanded Social Responsibility for Long-Term Care’, in VR Fuchs (ed), Individual and Social Responsibility, University of Chicago Press, Chicago, pp 143–169.
Garber AM and TA MaCurdy (1990), ‘Predicting Nursing Home Utilization among the High-Risk Elderly’, in DA Wise (ed), Issues in the Economics of Aging, University of Chicago Press, Chicago, pp 173–200.
Geanakoplos J, M Magill and M Quinzii (2004), ‘Demography and the Long-run Predictability of the Stock Market’, Brookings Papers on Economic Activity, 1, pp 241–325.
Go K (2003), ‘The Introduction of Market Mechanisms for Long-Term Care Services’, in Aged-ing In Japan, Research Booklet, AGHE Annual Conference on ‘AGHE Means Business: Educational Opportunities and the World of Work’, St. Petersburg FL, pp 231–239.
Green R and PH Hendershott (1996), ‘Aging, Housing Demand, and Real House Prices’, Regional Science and Urban Economics, 26(5), pp 465–480.
Hamilton BW (1991), ‘The Baby Boom, the Baby Bust, and the Housing Market: A Second Look’, Regional Science and Urban Economics, 21(4), pp 547–552.
Hendershott PH (1990), ‘Are Real House Prices Likely to Decline by 47 Percent?’, Regional Science and Urban Economics, 21(4), pp 553–563.
Holland AS (1991), ‘The Baby Boom and the Housing Market: Another Look at the Evidence’, Regional Science and Urban Economics, 21(4), pp 565–571.
Horneff WJ, R Maurer, OS Mitchell and I Dus (2006), ‘Optimizing the Retirement Portfolio: Asset Allocation, Annuitization, and Risk Aversion’, Pension Research Council Working Paper No 2006-10.
JILI (Japan Institute of Life Insurance) (2003), ‘Survey on Life Insurance in FY 2003’ (in Japanese). Available at <http://www.jili.or.jp/>.
Lachance M-E and OS Mitchell (2003), ‘Understanding Individual Account Guarantees’, American Economic Review, Papers and Proceedings, 93(2), pp 257–260.
Lachance M-E, OS Mitchell and K Smetters (2003), ‘Guaranteeing Defined Contribution Pensions: The Option to Buy-Back a Defined Benefit Promise’, Journal of Risk and Insurance, 70(1), pp 1–16.
Lakdawalla D and T Philipson (2002), ‘The Rise in Old-Age Longevity and the Market for Long-Term Care’, American Economic Review, 92(1), pp 295–306.
Lee K (2003), ‘LTC Insurance Providers Try to Come Up with New Twists’, Employee Benefit News, December. Available at <http://www.benefitnews.com/supplemental/detail.cfm?id=5385>.
MacDonald AS (1997), ‘United Kingdom’, in AS MacDonald (ed), The Second Actuarial Study of Mortality in Europe, Groupe Consultatif des Associations d'Actuaires des Pays des Communautés Européennes, Oxford, pp 177–200.
Mankiw NG and DN Weil (1989), ‘The Baby Boom, the Baby Bust, and the Housing Market’, Regional Science and Urban Economics, 19(2), pp 235–258.
McCarthy D and OS Mitchell (2002), ‘Estimating International Adverse Selection in Annuities’, North American Actuarial Journal, 6(4), pp 38–54.
McCarthy D and OS Mitchell (forthcoming), ‘International Adverse Selection in Life Insurance and Annuities’, in S Tuljapurkar, N Ogawa and A Gauthier (eds), Riding the Age Waves: Responses to Aging in Advanced Industrial States, Elsevier.
McCarthy D, OS Mitchell and J Piggott (2002), ‘Asset Rich and Cash Poor in Singapore? Retirement Provision in a National Defined Contribution Pension Fund’, Journal of Pension Finance and Economics, 1(3), pp 197–222.
McKibbin WJ (2005), ‘The Global Macroeconomic Consequences of a Demographic Transition’, in G-20 Workshop on Demographic Challenges and Migration, AGPS, Canberra, pp 13–52.
Merlis M (2003), ‘Private Long-Term Care Insurance: Who Should Buy It and What Should They Buy?’, Report to The Kaiser Family Foundation.
Milevsky MA and VR Young (2001), ‘The Real Option to Delay Annuitization: It's Not Now-or-Never’, Schulich-Finance Working Paper No MM11-1.
Mitchell OS and JF Moore (1998), ‘Can Americans Afford to Retire? New Evidence on Retirement Saving Adequacy’, Journal of Risk and Insurance, 65(3), pp 371–400.
Mitchell OS and J Piggott (2004), ‘Unlocking Home Equity in Japan’, Journal of the Japanese and International Economies, 18(4), pp 466–505.
Mitchell OS, J Piggott and S Shimizutani (2006), ‘Aged-Care Support in Japan: Perspectives and Challenges’, Benefits Quarterly, 22(1), pp 7–18.
Moore JF and OS Mitchell (2000), ‘Projected Retirement Wealth and Saving Adequacy’, in OS Mitchell, B Hammond and A Rappaport (eds), Forecasting Retirement Needs and Retirement Wealth, University of Pennsylvania Press, Philadelphia, pp 68–94.
Murtaugh C, B Spillman and MJ Warshawsky (2001), ‘In Sickness and In Health: An Annuity Approach to Financing Long-Term Care and Retirement’, Journal of Risk and Insurance, 68(2), pp 225–253.
Nishiyama S and K Smetters (2005), ‘Does Social Security Privatization Produce Efficiency Gains?’, NBER Working Paper No 11622.
Pauly MV (1990), ‘The Rational Nonpurchase of Long-Term Care Insurance’, Journal of Political Economy, 98(1), pp 153–168.
Poterba JM (2001), ‘Demographic Structure and Asset Returns’, Review of Economics and Statistics, 83(4), pp 565–584.
Poterba JM (2004), ‘The Impact of Population Aging on Financial Markets’, in GH Sellon Jnr (ed), Global Demographic Change: Economic Impacts and Policy Challenges, Proceedings of a Symposium Sponsored by the Federal Reserve Bank of Kansas City, Kansas City, pp 163–216.
Pratt JR (1999), Long-Term Care: Managing across the Continuum, Aspen Publications, Gaithersburg.
Rappaport A and J Stanger (1997), ‘Postemployment Benefits’, Compensation and Benefits Management, 13(1), pp 62–68.
Rovner J (2003), ‘U.S. Bill Would Encourage Long-Term Care Insurance’, Reuters, 15 May. Available at <http://www.reutershealth.com/archive/2003/05/15/eline/links/20030515elin015.html>.
Scobie GM and JK Gibson (2003), ‘Retirement Wealth of New Zealand Households: An Initial Analysis Based on the Household Savings Survey’, paper presented to a Symposium on Wealth and Retirement sponsored by the Office of the Retirement Commissioner, Wellington, 13 June.
Shiller RJ (1998), ‘Social Security and Institutions for Intergenerational, Intragenerational and International Risk Sharing’, Cowles Foundation Discussion Paper No 1185.
Siegel JJ (2005), The Future for Investors: Why the Tried and the True Triumph over the Bold and the New, Crown Business, New York.
UN Population Division (2005), World Population Prospects: The 2004 Revision, United Nations, New York. Available at <http://esa.un.org/unpp/>.
Valdés-Prieto S (2005), ‘Securitisation of Taxes Implicit in PAYG Pensions’, Economic Policy, 42, pp 215–265.
Warshawsky MJ, BC Spillman and CM Murtaugh (2002), ‘Integrating Life Annuities and Long-Term Care Insurance: Theory, Evidence, Practice, and Policy’, in OS Mitchell, Z Bodie, PB Hammond and S Zeldes (eds), Innovations in Retirement Financing, The University of Pennsylvania Press, Philadelphia, pp 198–221.
Wiener JM, L Hixon Illston and RJ Hanley (1994), Sharing the Burden, Brookings Institution Press, Washington DC.