RBA Annual Conference – 2006 Demographic Change, Saving and Asset Prices: Theory and Evidence[1] Axel Börsch-Supan
Abstract
Population ageing and pension reform will have profound effects on international capital markets. First, population ageing alters the time path of aggregate savings within individual countries. Second, this process may be amplified when a pension reform shifts old-age provision towards more pre-funding. Third, while the patterns of population ageing are similar in most countries, timing and initial conditions differ substantially. Hence, to the extent that capital is internationally mobile, population ageing will induce capital flows between countries. All three effects influence the rate of return to capital and interact with the demand for capital in production as well as the supply of labour.
In order to quantify these theoretical effects, the Mannheim Research Institute for the Economics of Aging (MEA) has developed a computational multi-country overlapping generations (OLG) general equilibrium model. We feed this model with detailed long-term demographic projections for seven world regions and compute the time paths of saving, capital flows and returns to productive capital as demographic change proceeds. Our simulations indicate that capital flows from fast-ageing regions to the rest of the world will initially be substantial but that trends are reversed when households decumulate savings. We also conclude that closed-economy models of pension reform miss quantitatively important effects of international capital mobility.
As an alternative, we also present econometric results from a panel of national time series in which saving rates, rates of return and international capital flows are related to anticipated demographic change. These estimates support the results from the multi-country OLG model.
1. Introduction
Populations in the G-20 countries are ageing. This demographic change will continue well into the 21st century. While population ageing is common to all G-20 countries, its extent and timing differs substantially between countries. Demographic change will alter the time path of most aggregate macroeconomic variables, including growth, savings and investment. In a world of closed economies, differences in demography will generate differences in growth, saving and investment rates between countries. Differences across countries are likely to be accentuated when some countries implement fundamental pension reforms – that is, shifts towards more pre-funding, induced by the effects of population ageing on public pension budgets – and others do not.
In reality, we do not live in a world of closed economies. To the extent that capital is internationally mobile, population ageing will induce capital flows between countries. These capital flows will modify the effects of population ageing and pension reform in each county vis-à-vis a world of closed economies. Global capital flows will affect saving rates, accumulated capital stocks, capital holdings and – significantly for the so-called ‘asset-price meltdown’ debate – rates of return. It is commonly argued that these international capital flows will help to attenuate cross-country differences. From the perspective of the G-20 countries, they are therefore a welcome mechanism to alleviate the pressures of population ageing.
The core of this paper presents a quantitative analysis of the capital and labour market effects of different ageing processes and pension reforms across countries, with a particular focus on international capital flows. To this end, we present simulation results from a stylised multi-country overlapping generations (OLG) model called MEA-OLGA (see Börsch-Supan, Ludwig and Winter 2002, 2004, forthcoming), which projects macroeconomic aggregates such as international capital flows over a 70-year horizon, using long-term demographic projections for different sets of countries and regions. Although all countries and regions are modelled symmetrically as large open economies, our discussion focuses on continental Europe, for two reasons. First, it is one of the regions most severely affected by ageing and, second, its pension systems are still dominated by relatively generous pay-as-you-go (PAYG)-financed public pensions.
The simulation results are then compared with an econometric analysis (Lührmann 2006) that uses past international capital flows and their dependence on past and expected demographic changes to project future international capital flows.
The analyses in this paper are related to several recent papers that compare implications for capital flows predicted by OLG models with actual current account data (for example, Brooks 2003; Feroli 2003; Henriksen 2002; Domeij and Flodén 2006). In common with our findings, these papers show that calibrated OLG models can explain a good fraction of the low-frequency movements of international capital flows observed in the data. We further show that the existence of PAYG pension systems in different world regions adds an additional, indirect, channel to the interaction between capital flows and demographic change. This channel is of particular importance if countries severely affected by the impact of population ageing, such as the continental European countries, reform their pension systems.
This paper also adds to the discussion about the so-called ‘asset-price meltdown’ hypothesis. Several articles in the popular press have attributed recent turbulence in stock market prices to population ageing and raised the prospect that an asset-price meltdown might occur when the baby boom generation decumulates its assets. In the academic literature, there is no consensus on the asset-price meltdown hypothesis (see, for example, Poterba 2001; Abel 2001, 2003; Brooks 2002). According to our view, the closed-economy models often used in the academic literature miss the important influence of international capital flows on domestic asset prices. We show that, because of international diversification, the dynamics of capital accumulation and rates of return in open-economy models are different from what would be predicted by closed-economy models. One of the main goals of this paper is to analyse and quantify these mechanisms.
Finally, this paper sheds light on the effects of international diversification on saving behaviour and its interaction with pension reforms. This topic has received increasing attention as the pension reform debate has progressed. For example, Deardorff (1987) contains an early analysis and Reisen (2000) provides a comprehensive overview of these issues. Reisen argues that there are pension-improving benefits of global asset diversification. In a theoretical paper, Pemberton (1999) highlights the importance of international externalities caused by the effects of national pension and savings policies on the world interest rate.
Our results, from simulations as well as econometric estimates, show that capital flows due to population ageing will be substantial. Population ageing results in decreases in saving rates when the baby boomers decumulate their assets. International capital flows follow this trend. The countries and regions most affected by ageing, such as the European Union, will initially export capital, while countries less affected by ageing, like the United States and other OECD regions, will import capital. However, since older households decumulate their assets, capital exports from these fast-ageing countries will eventually decrease; around the year 2020 fast-ageing countries are projected to become net capital importers. Pension reforms encouraging higher degrees of pre-funding are likely to induce more capital exports. They also increase the supply of labour considerably, while the effects on the rate of return to capital are small. While the rate of return is projected to decline in response to population ageing, we cannot find a convincing case to project a devastating ‘asset-price meltdown’.
The rest of the paper is structured as follows. Section 2 begins with a short review of the asset-price meltdown debate. Section 3 presents empirical evidence on, and theoretical explanations for, the effects of population ageing on international capital flows. In Section 4, we present a multi-country OLG model that allows us to evaluate these effects quantitatively. Section 5 contains our first set of results: simulations of international capital flows, saving rates and returns to productive assets for several pension policy and capital mobility scenarios. Section 6 presents a sensitivity analysis. Section 7 compares the OLG results with econometric evidence derived from a panel of national time series. Section 8 concludes.
2. The Asset-price Meltdown Debate
The effects of population ageing on the markets for real and housing capital are complex and can only be understood in a general equilibrium context. If elderly people save less than younger people, an ageing society saves less. By itself, this should increase interest rates since the supply of funds gets tight. At the same time, however, the size of younger generations becomes ever smaller, so there is also less demand for new investment. The overall effect is thus uncertain.
Pessimists believe in the so-called ‘asset-price meltdown’ hypothesis: households' demand for financial assets will plummet between 2030 and 2040, when the baby boomers retire and die. As a consequence asset values will collapse and the return on financial investments will fall sharply.
Optimists stress economic mechanisms which soften or even reverse the negative impacts of ageing on capital markets. One such important counter-mechanism is an ageing society's need for capital as a substitute for increasingly scarce labour. This rising demand for physical capital increases the return to capital at exactly the same time as pessimists fear the prospect of an asset-price meltdown.
A spectacular fall in the price of assets as a result of demographic change was first predicted in 1989 by Mankiw and Weil (1989) in the context of the real estate market in the United States. In theory, returns to real estate should be more affected by demographic change than returns to physical capital because there is much less room for international diversification and because housing cannot substitute for scarce labour. Mankiw and Weil used cross-sectional data on real estate assets from the 1970 US Census to develop an age profile of the demand for property. Their demand forecast is based on the assumption that this age profile remains constant and it is only the size and age structure of the US population that will change. Based on the historical correlation between the growth in demand for housing with the price index for investment in residential buildings, Mankiw and Weil conclude that the demand for residential property must increase by approximately 1.5 per cent per year to keep prices constant. However, the demographically controlled demand variable shows consistently lower growth rates for the period 1990–2010. They conclude that this forecast discrepancy exercises enormous price pressure on the residential property market. The point estimate by Mankiw and Weil implies a 47 per cent price fall within 20 years.
The study sparked a lively debate, which ultimately cast considerable doubt on the forecasts of Mankiw and Weil (1989, 1992). Woodward (1991) grouped together the main points of criticism in the first series of responses refuting the study. In this volume, both Hamilton (1991) and Hendershott (1991) noted that the estimates of Mankiw and Weil imply that, even if demand remains at a constant level, house prices would fall by 8 per cent. This implausible linear time trend has a much greater influence on the forecast than the decline in the annual growth of demand from 1.6 per cent at the start of the 1980s to around 0.6 per cent in 2000. Swan (1995) argues that not only were the effects of a long-term rise in real income completely ignored but the supply side of the residential property market was also not taken into account.
Engelhardt and Poterba (1991) also cast doubt on the findings of Mankiw and Weil. They provide an equivalent analysis for Canada, a country with demographic trends that largely mirror those in the US. The age profile of real estate assets in Canada also broadly corresponds to the equivalent profile in the US. In spite of this, Engelhardt and Poterba cannot find any similar influence of demography on house prices in Canada along the lines identified by Mankiw and Weil for the US.
More recent research highlights the importance of income and cohort effects. Mankiw and Weil's use of cross-sectional data to analyse the demand for residential property over the life-cycle ignores the effects of income and age cohort groups, which have proved to be very important in quantitative terms. In cross-sectional data (that is, data from many people observed at a single point in time), it is not possible to determine whether the elderly save more than the young, for example, because they are old (the age effect) or because they were born a long time ago at a time when, for instance, thrift was considered to be particularly virtuous (the cohort effect).
If one applies this approach to demand for residential property, it is impossible to tell whether an old person uses a small amount of living space because they do not need a large apartment when they are old or whether they do not have a large apartment in old age because when they purchased their apartment they did not have enough real income to afford a large apartment. In their analysis, Mankiw and Weil present the cross-sectional profile of real estate assets in 1980 by way of comparison. However, the assets values of census data in 1980 were, on average, more than 50 per cent above the 1970 sample group for each age group. When it comes to using demand profiles for fairly long-term forecasts, a difference of this order of magnitude shows the quantitative significance of income-related effects and other cohort effects more generally. The increase in the value of asset profiles for all age groups between 1970 and 1980 illustrates the extent to which the demand for real estate could also change in the future.
Studies from the US that adopt a more careful approach than Mankiw and Weil verify that, for just these reasons, the estimates of age-specific demand for residential accommodation are distorted and a possible ‘asset-price meltdown’ effect is greatly exaggerated – for example, see Venti and Wise (1990), McFadden (1994) and Skinner (1996). Börsch-Supan, Ludwig and Sommer (2003) apply a similar approach for Germany and obtain similar results, although Germany ages faster than the US.
The ultimate judge, of course, is time. Hence it is worth noting that the forecast ‘asset-price meltdown’, which should have occurred between 1990 and 2010 in the US, has simply not occurred (as of September 2006), neither during the boom in equity markets (which is easy to explain), nor since the bubble burst (which is a more significant refutation of Mankiw and Weil's claim).
Turning to productive capital, the most familiar study based on empirical data of saving behaviour over the life-cycle is the analysis by Poterba (2001). He derives a demand variable from the shift in the age structure of the population, which is produced from an estimated life-cycle savings profile. In contrast to Mankiw and Weil, Poterba estimates the demand from the various age classes in a model which permits explicit cohort effects. The estimated asset profile in old age is largely flat – a result that had already been documented by other authors. Poterba also incorporates a series of other demographic variables that can explain the accumulation of savings in a society. Using a long time series he finds hardly any indication that demography influences returns to equity and only minimal indications of such influences on the market for interest-bearing securities. The only variable for which Poterba found demography had historical influences was the price-earnings ratio of equities, and even here the relationships are not stable. Poterba concludes that a demographically induced fall in asset prices, as predicted by Mankiw and Weil for the real estate market, is extremely unlikely.
Abel (2001) is critical of Poterba's analysis. He sets up a theoretical model in which households are interested in the well-being of their heirs and thus possess a bequest motive. He shows that it is entirely possible for an asset-price meltdown to be consistent with a flat asset profile in old age. Although the older generation's demand for capital is not falling, a demographically induced fall in prices could occur through lower saving by the younger generation. However, there is no evidence that inheritances will fall with the number of children. Abel's theoretical countermechanism to Poterba's analysis thus seems to be of little empirical relevance.
3. Population Ageing and International Capital Flows
Throughout the world, demographic processes are determined by a demographic transition characterised by falling mortality rates followed by a decline in birth rates, resulting in population ageing and a fall in the population growth rate (in some countries, even turning it negative). While demographic change is occurring in almost all countries, its extent and timing differ substantially. Europe and some Asian countries have almost passed the closing stages of the demographic transition process while Latin America and Africa are only at the beginning stages (Bloom and Williamson 1998; UN Population Division 2001).
From a macroeconomic perspective, population ageing will change the balance between capital and labour, particularly in industrialised countries. Labour supply will become relatively scarce whereas capital will become relatively abundant. This will drive up wages relative to the rate of return to capital, reducing households' incentives to save (if the interest elasticity of saving is positive). In addition, a decreasing labour supply reduces the demand for investment goods since less capital is needed to achieve any given capital-labour ratio.
From a microeconomic point of view, the life-cycle theory of consumption and savings (Modigliani and Brumberg 1954; Ando and Modigliani 1963) predicts that saving rates will decline as individuals enter old age. The aggregation of individual, cohort-specific life-cycle savings profiles therefore leads to a decrease of national saving rates in an ageing economy. In a general equilibrium model of forward-looking individuals, it is not only the current demographic structure that alters the time path of aggregate savings, but also future demographic developments. In a closed economy, a decline in national saving leads to a decline in investment by definition. In an open economy, the link between these two aggregates is broken to the extent that capital is internationally mobile.
Empirical evidence lends support to these theoretical mechanisms, as discussed in the paper by Poterba (2001). Following earlier work by Higgins (1998) and others, Lührmann (2006) investigates whether demography influenced international capital flows in the past, using a broad panel of 141 countries over the period 1960–1997. She confirms that cross-country capital flows are indeed influenced by current demographic variables. Moreover, she shows that future changes in population age structures are important determinants of current saving and investment decisions, suggesting that households respond to changes in demography in a forward-looking manner.
The extent to which population ageing induces international capital flows depends crucially on the degree of capital mobility. There has been no shortage of empirical research on this issue since the famous puzzle of Feldstein and Horioka (1980).[2] In their original contribution, Feldstein and Horioka show that national saving and investment rates are highly correlated in virtually all OECD countries. While the correlations have fallen over time, they are still remarkably high in many countries. These findings have been interpreted as an indication that capital is imperfectly mobile. However, there exist several alternative explanations for the observed correlation. For example, high correlations between saving and investment rates are consistent with perfect capital mobility in a growth model with demographic change and technological progress, as pointed out by Obstfeld (1986) (see also Baxter and Crucini 1993; Taylor 1994; Obstfeld and Rogoff 1996, 2001).
Even if capital is fully mobile, this does not necessarily imply that households diversify their portfolios optimally. There is a large empirical literature on ‘home bias’ in international portfolio choice (for example, French and Poterba 1991). Portes and Rey (2005) suggest that information asymmetries across countries are a major source of home bias and that geographic and informational proximity both affect international capital flows. Applied to pension reform policies, this literature suggests that households might be more willing to invest their retirement savings in ‘similar’ countries. In the case of European households, this could result in a preference for investing in the EU or OECD countries rather than in developing countries.
The background facts and empirical insights from this section motivate our modelling strategy, which is detailed in the following section, including our calibration choices.
4. A Dynamic, Open-economy Macroeconomic Model
The previous sections have shown that savings, capital returns and international capital flows are the outcome of complex interactions between supply and demand in domestic and international capital markets. These interactions also depend on demographic factors. One actually needs a simulation model in order to understand these equilibrium effects since relative quantities matter even for qualitative results. This section, based on Börsch-Supan et al (2002, 2004, forthcoming) determines the general equilibrium by drawing on an OLG model of households. Such OLG models have a long tradition. The theory underpinning these models was developed by Samuelson (1958) and Diamond (1965). This was extended by Auerbach and Kotlikoff (1987) who, for the first time, used an OLG model in a near-reality computer simulation. The MEA-OLGA simulation model, on which the results of this section are based, was the first such model that is not restricted to one country but also covers international trade and capital movements. Details, including a mathematical description, of the latest version of the MEA-OLGA model can be found in Börsch-Supan et al (forthcoming). Here we limit ourselves to describing the essential mechanisms and equations for this model. It should be noted that this model takes a long-term perspective and thus abstains from all short-term Keynesian considerations. An important implication of this is that exchange rates have no role to play in our economic model.
4.1 How households behave
The households in the MEA-OLGA model offer a fixed amount of work. They divide their income between consumption and saving but here we only map long-term saving decisions, that is the savings that are required to compensate for the drop in income upon retirement. The accumulation of savings is therefore determined by the life-cycle hypothesis in which a household does not apportion its income into consumption and saving each year but rather over a time scale that depends on the household's discount rate. Consumption in period t, Ct, is smoothed according to this long-term plan so that it greatly depends on consumption in the preceding period, Ct–1. Impatient consumers (whose discount rate, ρ, exceeds the market interest rate, rt) initially consume a large amount. In contrast, patient households (whose discount rate is lower than the market rate) initially save a lot. The development over time of consumption is described by the following simple equation in which the ratio between the discount rate and the market interest rate is weighted by the parameter σ:
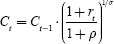
This consumption equation also implicitly describes the saving decision because current income minus current consumption expenditure gives the value of saving. This is added to the stock of current assets (plus interest) to obtain the next period's stock of assets:
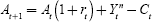
In many countries, PAYG retirement insurance schemes have a crucial influence on saving decisions because they form a major source of income during retirement. This is supplemented by cashing-in household savings (in the case of Germany, this may include income from ‘Riester pensions’). Our model only maps long-term savings in the form of provisions for old age. If the PAYG retirement insurance scheme is so generous that pensions replace 100 per cent of pre-retirement income, no long-term saving occurs in our model. If, at the other extreme, the level of the public pension falls to zero, all income in old age must be provided by private savings, and consumption is correspondingly lower in younger years.
Savings are invested in productive capital. These investments can either occur domestically or abroad. The model assumes that capital moves to where the returns, after accounting for risk and tax, are the highest and that international capital flows will continue until these returns are the same in all countries.
4.2 Production, capital markets and overall economic balance
On the production side, capital and labour are used as substitutes so that wages correspond to marginal labour productivity and capital returns correspond to marginal capital productivity. Production is described by a Cobb-Douglas production function, which converts Lt,i and capital Kt,i into units of goods and services, measured as gross domestic product (GDP), Yt,i. The indices t, i and a stand for year, country and age, respectively.
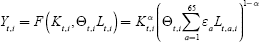
All countries have the same production technology, F, but labour productivity, Θt,i, varies. Also, the entire workforce Lt,i is composed of the various age groups, Lt,a,i, whose age-specific productivities, εa, correspond to the average wage profile.[3]
The different productivity levels, Θt,i, correspond to the different per capita GDPs. The available quantity of labour supplied by individuals in each age group, Lt,a,i is derived from the demographic assumptions.[4]
Wages and interest rates are determined by labour productivity and capital productivity, respectively. In particular, the interest rate is equal to the marginal productivity of the capital deployed minus the rate of depreciation δ:[5]
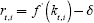
Domestic investment is defined as the net change in the domestic capital stock:
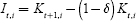
Capital Kt,i, which is used in country i for production, does not have to correspond to the assets that the inhabitants of that country have accumulated and which we have described as At,i. The difference
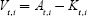
represents the net foreign asset position of domestic residents. If a country saves more than it invests, capital flows abroad – for instance, in the form of direct investments – until returns, adjusted for risk and tax, have converged in all countries. A country's current account balance is therefore
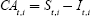
If one takes all the regions of the world together, both the international capital flows and the net external positions of the various countries must cancel each other out, because the regions of the world form a closed economy. This provides the key condition for the equilibrium of international trade in our model; that is:
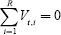
The MEA-OLGA model parameters are calibrated so as to match the overall economic pattern in Germany from 1970 to 1995. The relevant parameters are listed and explained in Börsch-Supan et al (forthcoming).
4.3 How international capital movements are modelled
We first applied the MEA-OLGA model to three scenarios for capital mobility: firstly, to Germany as a closed economy; secondly, to Germany as an open economy with perfect capital mobility within the countries of the EU; thirdly, with perfect capital mobility within the countries of the OECD. Although perfect capital mobility within the OECD may not occur, this is probably a reasonable assumption for the EU, because most capital flows occur within the euro area where there is free movement of capital. Focusing on euro-area economies allows us to ignore the impact of exchange rates in the MEA-OLGA model. Even in broader scenarios, this assumption may be reasonable as the model describes very long-term trends in capital movements. Short-term exchange rate movements induce flows of capital which, although considerable, are of short duration and of less interest to us. Long-term exchange rates and capital flows are, however, determined jointly by fundamental variables, such as demography and overall economic development.
4.4 How further capital is accumulated as a result of old-age provision
We mapped the potential scope for the development of pension insurance with two scenarios. The first scenario (‘retain PAYG systems’) assumes that countries retain PAYG pension systems providing replacement rates of approximately 70 per cent of pre-retirement income (roughly equivalent to the situation in Germany before the ‘Riester reform’. In this scenario, contribution rates increase from 19.5 per cent to 25.7 per cent in the year 2030 to finance ageing-related additional costs. We call the second scenario the ‘freezing model’. This systematic reform model stabilises the contribution rate at 19.5 per cent, so that the PAYG replacement rates fall to just under 51 per cent. At the same time, overall retirement incomes remain constant via a gradual transition to a pension system based on a substantially higher funded component. These are obviously two extreme scenarios. In most countries, political pressures will not permit a situation where contribution rates rise to almost 26 per cent. However, it is also unlikely that contribution rates can be frozen, so the most probable social policy development will be for systems to find a balance between these two extremes.
4.5 Calibration
In order to capture projected international differences in demographic characteristics and the generosity of public pension systems, we distinguish seven world regions in the benchmark scenario: (i) France, (ii) Germany and (iii) Italy as three large European countries severely affected by population ageing, (iv) the remainder of the European Union, (v) North America (the US and Canada), (vi) remaining OECD countries, and (vii) all other countries in the world. While we treat France, Germany and Italy as separate regions in the simulations, we simplify the presentation of most of our simulation results by aggregating them into a combined France-Germany-Italy (FGI) region.
Our demographic model for these regions is calibrated to fit UN Population Division (2001) projections. These projections end in 2050. Between 2050 and 2100, we continue the linear increase in life-expectancy assumed by the UN and impose constant fertility rates at the levels reached in 2050. During the phase-out period of the model beyond 2100, demographic processes adjust so that stable populations are reached by 2200.[6]
PAYG pension systems are calibrated with data on replacement rates taken from Palacios and Pallarès-Miralles (2000) and employees' social security contributions taken from the OECD (2001). We solve for equilibrium contribution rates using the PAYG budget constraint.
Further parameters of the model describe the households' preferences, the parameters of the production function and the age-specific productivity profile. For the latter, we use the cohort-corrected non-linear regression estimates by Fitzenberger et al (2001). This provides us with a representative age-wage profile that peaks at the age of 55 and then decreases slightly.
With two exceptions, technological and preference parameters are assumed to be constant and equal across all countries. The values of these parameters are standard in the literature and summarised in Table 1. The annual growth rate of labour productivity, g, is set to 1.5 per cent, which is slightly higher than the value of 1.4 per cent suggested by Cutler et al (1990) and closer to the long-run projections suggested by the OECD. The capital share parameter, α, is set to an intermediate value of 0.35. The annual depreciation rate of capital, δ, is assumed to be 5 per cent per year.
| α: output share of capital in the CES production function | 0.35 |
|---|---|
| g: growth rate of labour productivity | 0.015 |
| δ: depreciation rate of capital | 0.05 |
| ψ: adjustment cost parameter | 1.5 |
| ρ: rate of time preference | 0.01 |
| σ: coefficient of relative risk aversion | 2 |
| ξ: intratemporal substitution elasticity | 0.8 |
| Θi: technology level | 0.05–0.07 |
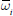 : consumption share
parameter : consumption share
parameter |
0.535–0.665 |
| Δωi: increment of consumption share parameter | 0.015–0.02 |
The adjustment cost parameter, ψ, is set to the value of 1.5 and results in a steady-state value of Tobin's q of 1.0975, which is in the middle of the values used in the literature. As we show in an extensive sensitivity analysis (Börsch-Supan et al 2004), adjustment costs allow us to study the time paths of the price of capital, but otherwise do not affect the long-run equilibrium results.
The rate of time preference in all countries, ρ, is set to 0.01, which is close to the estimate of 0.011 in Hurd (1989). With this choice – and given all the other parameter values – our calibrated model produces an average capital-output ratio of about 2.9 for the ‘European Union’ region over the period 1960–2001. While comparable capital-output ratios for a large cross-section of countries are not available, a value of 2.9 is reasonable for many countries (OECD 2004). The coefficient of relative risk aversion, σ, is set to 2, which is within the standard range of 1 and 4. We follow Altig et al (2001) in choosing the value for the intratemporal substitution elasticity ξ =1/(1+γ)= 0.8.
Levels of total factor productivity, Θi, vary across countries and are calibrated such that the model replicates output data in each country for the period 1960–2001.[7] The relative preferences for consumption and leisure in households' utility functions vary across countries and ages such that the simulation model approximately replicates aggregate labour supply as well as labour supply profiles across ages in each country for the period 1960–2001.
A final remark concerns the initial values of the model for the year 2002 under the different capital mobility scenarios. Conceptually, it is problematic to simulate a calibrated macroeconomic model under policy scenarios other than the one for which it was calibrated. In our case, the world for which we calibrate the model changes with the number of regions considered in the capital mobility scenarios. On the one hand, it would make sense to adjust the calibration parameters each time we change the number of regions that we consider. On the other hand, this would change households' reactions to changes in policy and it would therefore be more difficult to interpret our results with respect to a reform of public pension systems. Since we are primarily interested in the reaction of households to demographic change and fundamental pension reform, we hold parameter values constant across all capital mobility scenarios. We calibrate the model under the assumption that the ‘OECD’ capital mobility scenario correctly reflects the ‘true’ world and therefore that all other capital mobility scenarios are ‘counterfactual’ worlds. The careful reader will note that this procedure results in differences in the values of the simulated variables in 2002, the base year of our simulations.
5. Simulation Results for Alternative Pension and Capital Mobility Scenarios
In this section we present our main results: how will demographic change affect key macroeconomic variables? Since the speed and extent of demographic change varies across the world, we would observe different rates of return to capital in each region if the regions were closed economies.
In a world of open economies, however, differences in rates of return will induce international capital flows until returns are equal, allowing for tax and risk, in all regions. In order to illustrate the influence of capital mobility across regions, we build four capital mobility scenarios focusing on their impacts on the three largest economies in continental Europe (France, Germany and Italy). The first scenario corresponds to a situation where France, Germany and Italy can invest only in each other. The other three capital mobility scenarios open this closed economy up sequentially: France, Germany and Italy diversify their investments (i) across all countries of the EU, (ii) across all OECD countries, and (iii) across the entire world. The results in Figures 2–5 display lines representing these alternative capital mobility scenarios. The benchmark scenario assumes that capital mobility is restricted to the OECD area.[8]
In addition to these direct effects of demographic change, there are indirect effects due to the presence of (partially) PAYG-financed social security systems. In order to separate the direct effects of population ageing on capital markets from potential feedback effects due to the existence of pension systems and pension reform, we present our main results under two hypothetical pension policy scenarios (as described above): (a) an ‘old system scenario’ in which FGI maintain their existing current generous public pension systems; and (b) a ‘reform scenario’ that introduces a transition to a partially funded pension system by freezing contribution rates in these three countries. The other regions' pension systems remain unchanged. By comparing these two extreme scenarios, we can show that a good portion of the capital market effects of population ageing arise even without fundamental pension reform. Accordingly, the figures below have two panels. The top panel corresponds to the ‘old system scenario’, that is, the direct effects of demographic change and the lower panel shows the differences between these two scenarios, that is, the indirect effects of a fundamental pension reform (which is in turn driven by the pressures of demographic change).
The interplay between these direct and indirect effects of population ageing on macroeconomic variables is complicated because they involve changes in levels and trends. Direct level effects are due to differences in the levels of working-age population ratios across countries. Younger economies, that is, economies with higher working-age population ratios, have higher marginal productivities of capital that will be arbitraged away by international capital flows. Direct trend effects are related to the speed of demographic change and affect the dynamics of macroeconomic variables. As working-age population ratios decrease, capital-output ratios increase and both the rates of return and saving rates decline.
The indirect effects of PAYG-financed pension systems are due to the ‘crowding-out’ effect that the provision of old-age pensions has on private saving and the corresponding distortionary taxation of labour income. By crowding out private savings, the indirect level effect of a PAYG-financed pension system works in the opposite direction to the direct effect of demographic change. That is, relative to a situation without PAYG-financed pension systems, the indirect effect decreases the differences in saving rates and rates of returns between countries. The indirect trend effect occurs because, over time, old-age dependency ratio increases force contribution rates to PAYG pension systems to increase (since PAYG replacement rates are taken as given). The indirect trend effect is stronger in (older) regions that are currently ageing more rapidly and so are more severely affected by the impact of demographic change.
In order to illustrate the complex interactions between direct and indirect level and trend effects, the presentation of our results proceeds in several steps. Throughout, we focus on the economic consequences of ageing and of fundamental pension reform on the continental European region consisting of France, Germany and Italy. As our point of departure, we analyse the impact of exogenous demographic change on working-age populations and old-age dependency ratios. We then analyse the two ways in which households react to demographic change and fundamental pension reforms by examining how labour supply and saving patterns are affected. We next turn to the firm sector and analyse the evolution of wage rates and the return to capital as well as the price of capital, represented by Tobin's q. Then we focus on the differences between national saving and investment that generate international capital flows and describe how they are affected by demographic change. Our results demonstrate the potential for substantial flows between, and within, the different regions of the world. To highlight this aspect, we present results on saving patterns and international capital flows for France, Germany and Italy. We conclude this section with a brief welfare analysis for households living in Germany.
5.1 Point of departure: demographic change
Figure 1 shows the effects of demographic change on two central demographic measures – the share of persons of working age (15–65 years) out of the total population, and the old-age dependency ratio (the number of persons older than 65 as a share of the working-age population).
A number of lessons can be drawn from these measures. First, all world regions are affected by demographic change: the proportion of persons of working age will decrease and the old-age dependency ratios will increase. Second, while the shares of persons of working age were similar in 2000 among OECD countries, they are projected to diverge in the decades ahead. The decrease in the share of persons of working age is strongest in the EU, especially among France, Germany and Italy. Third, these three countries are also projected to have the highest old-age dependency ratios. Fourth, there are significant differences in the timing and pattern of demographic change across regions. As we will see, these different patterns have profound implications for the evolution of saving rates, rates of return and international capital flows.
5.2 Labour supply, contribution and replacement rates
These demographic changes have immediate effects on labour supply and the sustainability of pension systems. Labour supply shares in France, Germany and Italy are projected to decrease from 42 per cent currently to below 36 per cent by 2050. The economic dependency ratio, defined as the ratio of pensioners to workers, is projected to increase from roughly 50 per cent in 2002 to about 80 per cent in 2050.[9]
As a consequence of the decrease in labour supply shares and the resulting increase in the economic dependency ratio, contribution rates to PAYG pension systems increase sharply under the ‘old system scenario’. These contribution rates are equilibrium contribution rates, meaning that they ensure that the budget of the pension system of each country is balanced at every point in time (implicitly including tax subsidies to the pension system). The time patterns of net replacement and contribution rates for France, Germany and Italy that result from our procedure are summarised in Table 2.
| France | Germany | Italy | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2000 | 2030 | 2050 | 2000 | 2030 | 2050 | 2000 | 2030 | 2050 | |||
| Old system scenario | |||||||||||
| Contribution rates | 0.275 | 0.356 | 0.375 | 0.268 | 0.375 | 0.415 | 0.325 | 0.476 | 0.534 | ||
| Net replacement rates | 0.654 | 0.654 | 0.654 | 0.700 | 0.700 | 0.700 | 0.646 | 0.646 | 0.646 | ||
| Reform scenario | |||||||||||
| Contribution rates | 0.275 | 0.295 | 0.295 | 0.268 | 0.294 | 0.294 | 0.325 | 0.340 | 0.340 | ||
| Net replacement rates | 0.654 | 0.549 | 0.513 | 0.700 | 0.568 | 0.504 | 0.646 | 0.489 | 0.415 | ||
|
Note: Figures shown in the table refer to the open economy scenario ‘OECD’. Source: author's calculations |
|||||||||||
If current generous replacement rates were maintained, our model predicts that the equilibrium contribution rate in Germany would increase from its current level of roughly 27 per cent to 42 per cent by 2050 – an increase of more than 50 per cent. The stylised pension reform freezes contribution rates at the level reached in 2006, roughly at 29 per cent. As a result, average pension levels decrease: the net pension replacement rate is projected to decrease from 70 per cent in 2000 to about 50 per cent by 2050. Hence, for Germany, under this scenario our model predicts a one-third transition towards pre-funding by 2050. Results for the other countries are similar.
Households respond to these decreases in pension benefit levels by saving more and by increasing their supply of labour. The stylised pension reform would lead to substantial increases in aggregate labour supply. Labour supply shares are predicted to increase by more than 2.5 percentage points by 2050. This increase is roughly the same for all capital mobility scenarios. For instance, labour supply shares in the FGI region increase from about 36 per cent in the year 2050 under the ‘old system scenario’ to 38.5 per cent under the ‘reform scenario’. As a consequence, the economic dependency ratio is projected to decrease by almost 6 percentage points. Endogenous labour supply is therefore a helpful mechanism to dampen the effects of population ageing. This effect holds over the entire range of the crucial elasticity parameters in the MEA-OLGA model (Börsch-Supan et al 2004).
5.3 Savings and capital stock
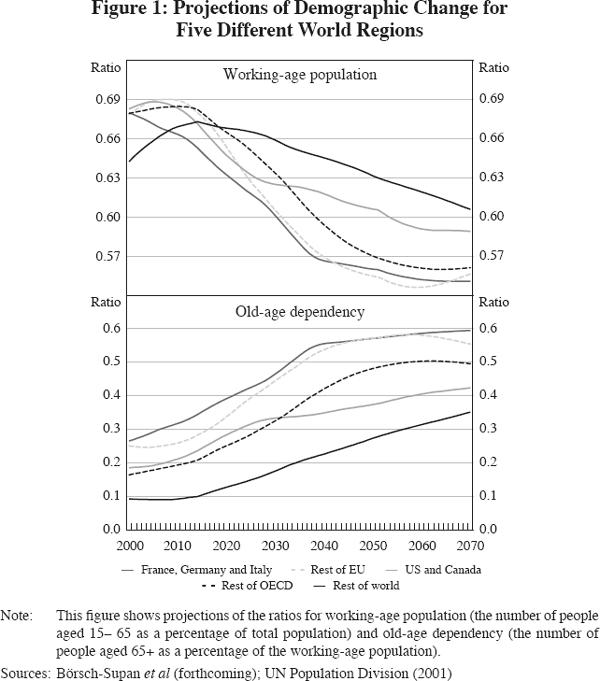
The top panel of Figure 2 shows the aggregate average saving rate of France, Germany and Italy in the four capital mobility scenarios. In the year 2000, saving rates are substantially higher in the open-economy scenarios than in the closed economy scenarios. This reflects the higher rates of return to capital realised in a more rapidly ageing open economy able to export capital to relatively younger economies.
This direct level effect is superseded by the demographic changes that occur during the 2000–2070 prediction window. Saving rates decrease until 2050 across all capital mobility scenarios, since the baby boom generation decumulates assets. Saving rates are projected to rebound after the year 2050. The decrease in the saving rate caused by population ageing – the difference between the value in 2000 and the minimum reached just after 2040 – is roughly 4.5 percentage points if capital mobility is restricted at most to the EU region (the FGI and EU scenarios). If we allow for capital mobility within the OECD or the entire world, this decrease is 6.5 or 8 percentage points, respectively. The larger declines in the open economy scenarios are due to the indirect trend effect described above. The advantages of worldwide capital mobility thus decline and saving rates respond accordingly.
Projected aggregate saving rates under a fundamental pension reform are substantially higher and the effect of a pension reform is stronger in the OECD and World open-economy scenarios (the saving rate is projected to increase by slightly more than one percentage point in the EU scenario as compared to 2 percentage points in the OECD and World scenarios). An increase in national savings leads to an increase in the capital stock and thereby a decrease in the rate of return to capital, which then discourages further savings. In those scenarios with a larger international capital market, substantially more savings are generated since – as we show below – the rate of return decreases by much less. These projections show that optimal life-cycle behaviour generates additional saving under a fundamental pension reform – in our model, it is not the case that additional retirement saving induced by a pension reform crowds out other saving totally, as has often been claimed.
We also accumulate aggregate savings across regions to obtain the world's asset holdings and capital stocks and the related capital-output ratios (not shown). In the OECD scenario, a consequence of decreasing the supply of labour is that the capital-output ratio increases from its current level of about 3 to about 3.25 by 2040 and then decreases slightly when baby boomers decumulate assets. This decrease is much more pronounced if we restrict the international capital market to the EU area only. Simultaneous fundamental pension reforms in France, Germany and Italy lead to substantial increases in the capital-output ratio if we restrict capital mobility to these countries or the EU area. The increase is much lower if we relax this constraint, suggesting that the additional savings shown in Figure 2 are largely invested abroad.
5.4 The rate of return and the price of capital
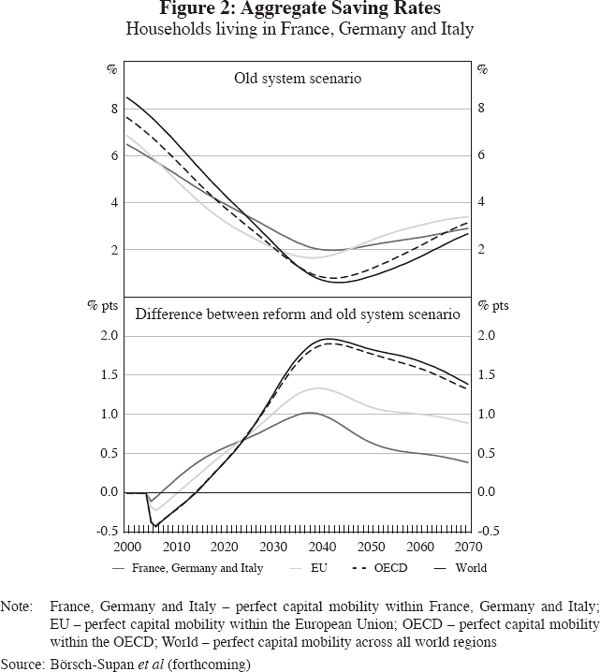
Much of the political and academic debate on the capital market consequences of demographic change and pension reforms has focused on the rate of return to capital, to which we turn next. First, we observe the same level effects as already described in the previous section. It is noteworthy that the demographic effect is larger than a second-level effect. Since the PAYG systems are slimmer in the aggregate rest-of-the-world region than in France, Germany and Italy, the capital stock accumulated for retirement savings is larger, which depresses rates of return.
Second, as a consequence of population ageing and the resulting increase in capital-output ratios, our model predicts that the rate of return to capital will decrease by a bit less than 1 percentage point if capital moves freely within the OECD (see Figure 3). This decrease hardly constitutes an ‘asset-price meltdown’. Third, while the rate of return decreases across all capital mobility scenarios, substantial gains would be possible if ‘older’ countries could ‘shift’ investments to ‘younger’ countries since our model predicts that savers in older countries can achieve higher returns if capital is mobile across all world regions. However, as demographic processes are highly correlated across countries (compare Figure 1), allowing for capital mobility across countries more or less only affects the level of the rate of return. Furthermore, diversification advantages decrease over time since indirect trend effects are at work as well.
As the lower panel of Figure 3 suggests, there would be an additional long-run decrease in the rate of return to capital if France, Germany and Italy simultaneously reformed their pension systems in a fundamental way. This decrease would amount to about 0.25 percentage points in 2070 if capital was freely mobile within these countries only. However, due to the response of labour supply to pension reform, this long-run decrease in the rate of return is lower than it would be in a model with exogenous labour supply (Section 6). In contrast to such a model, our model even predicts an increase in the rate of return until about 2030 or 2040 (as a result of the endogenous labour supply reaction). While saving rates immediately start to increase after the reform, labour supply increases as well. The net effect is an initial decrease in the capital-output ratio and an associated increase in the rate of return to capital. Moreover, and in line with earlier results in Börsch-Supan et al (2002), the decrease in the rate of return is negligibly small if capital moves freely across OECD countries (or the entire world).
Tobin's q, the price of capital, also decreases as a consequence of population ageing but its level is higher in the demographically younger regions. Results regarding Tobin's q for the FGI region are depicted in Figure 4. Notice that the relative decrease of q-values is lower under the pure PAYG scenario if capital is mobile across a greater part of the world (top panel). As a consequence of fundamental pension reforms, q-values are predicted to increase slightly since the investment to capital ratio increases (lower panel). The long-run effect is stronger if capital mobility is restricted to a smaller region.
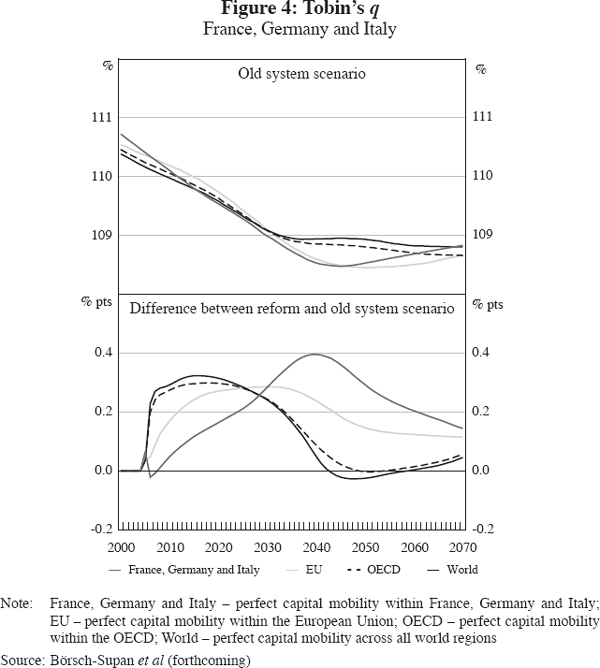
5.5 International capital flows
International capital outflows from France, Germany and Italy to other OECD countries roughly follow the pattern of saving rates and decrease steadily until 2050 (see Figure 5). In the OECD and World capital mobility scenarios, they are initially positive at about 2 and 3.2 percentage points of output. Over time, these net capital flows are reversed and the model predicts that France, Germany and Italy will run current account deficits of between 2 and 2.5 percentage points of output by 2050 (top panel).
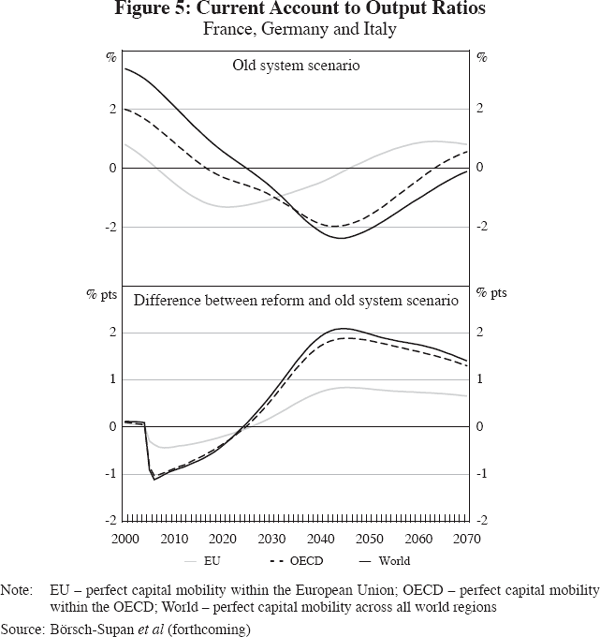
So far, our analysis has concentrated on France, Germany and Italy in aggregate. However, there are substantial differences across these countries. To highlight this, we next analyse savings patterns and international capital flows within the EU region under the assumption that the international capital market is restricted to the OECD area.
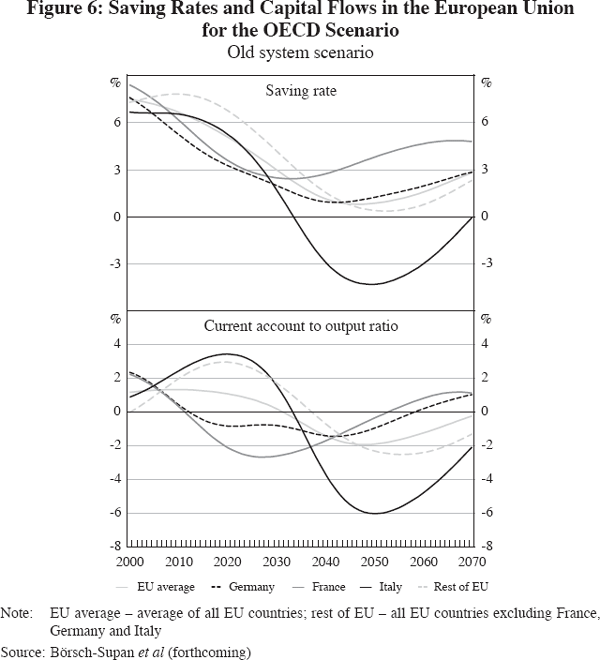
Figure 6 (top panel) shows saving rates for France, Germany, Italy, the remaining EU countries and the EU average. The time pattern of German saving rates roughly mirrors the EU average. Germany's saving rate is projected to decrease from current levels of 7 per cent of output to about 2 per cent of output by 2050. For France, the youngest of the three countries, the decline in its saving rate lasts only until 2030 and the overall decrease is smaller than in other EU countries. Italy, faced with the most rapid and extensive population ageing process within Europe, is at the other extreme: Italian households' saving rates are projected to become substantially negative in 2050.
5.6 Welfare analysis
Figure 7 shows the effects of the fundamental pension reform on remaining lifetime utility for different cohorts in Germany. We follow Altig et al (2001) and measure the change in remaining lifetime utility as the equivalent variation of income. That is, we construct an index that measures the present value of remaining lifetime resources relative to remaining lifetime resources under the old system that a household would have to receive (pay) under the new system to make it indifferent between the old and the new system. Therefore, an index number greater (smaller) than 1 implies a loss (gain) in remaining lifetime utility.
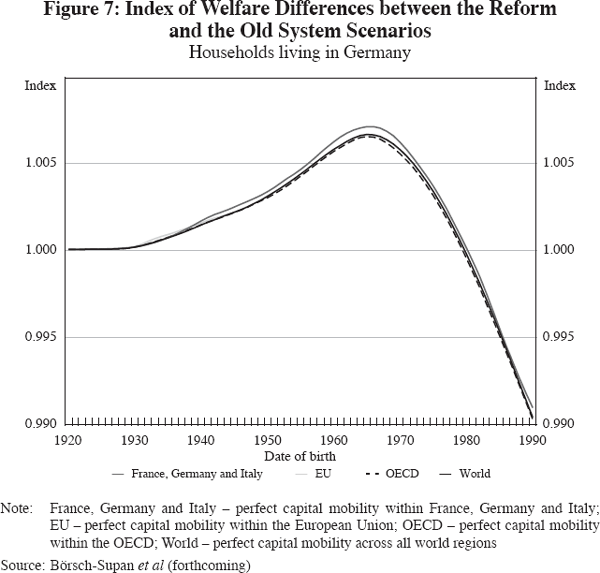
The results show that remaining lifetime utility of cohorts born between the years 1920 and 1990 decreases as a consequence of the fundamental pension reform. While substantial welfare gains are possible in the long run in all capital mobility scenarios, the figure also illustrates that fewer cohorts experience losses if capital mobility extends to more regions of the world. However, the difference between the alternative capital mobility scenarios is not large.
6. Sensitivity Analysis
One of the weaknesses of computational general equilibrium analysis is the dependence of the results on modelling strategies and parameter values. The usual response is an extensive sensitivity analysis. The existing literature has mostly concentrated on sensitivity analysis of simulation results with regard to values of structural (deep) model parameters, for example, Altig et al (2001). Applying this type of conventional sensitivity analysis to this paper shows that the results change very little when we vary the main elasticity parameters within their usual ranges. Our most contentious conclusion – the absence of a serious asset-price meltdown – is robust with respect to the choice of these elasticity parameters.[10]
In addition to this conventional sensitivity analysis, we also investigate the robustness of our results with respect to four key dimensions of our model specification. What difference does it make: if labour supply is endogenous or exogenous; if investment incurs adjustment costs; if perfect annuity markets absorb all accidental bequests; or if part of retirement income is provided by a PAYG pension system? We find that the first dimension – whether labour supply is endogenous – matters a lot for assessing the effects of a pension reform, while the other three dimensions – adjustment costs, annuity markets and accidental bequests – matter very little.
In the paper, we therefore only report on the role of endogenous labour supply. For simplicity, we concentrate on a three-region rather than a seven-region model as in the previous section: (i) France, Germany and Italy; (ii) all other EU countries; and (iii) all other OECD countries. We focus on the differential effects between the old system and the reform scenario because this is where the endogeneity of labour supply matters most.
Figure 8 compares the saving rates and rates of return generated by models with endogenous and exogenous labour supply. In the exogenous labour supply specification, we hold age-specific labour supply shares constant at levels obtained in the endogenous labour supply scenario in the year 2000. We first show the reaction of saving to the fundamental pension reform. As depicted in Figure 8 (top panel), the increase of the saving rate is much larger if labour supply is exogenous – not surprising perhaps given that with labour supply fixed saving is the only means by which to adjust to the pension reform.
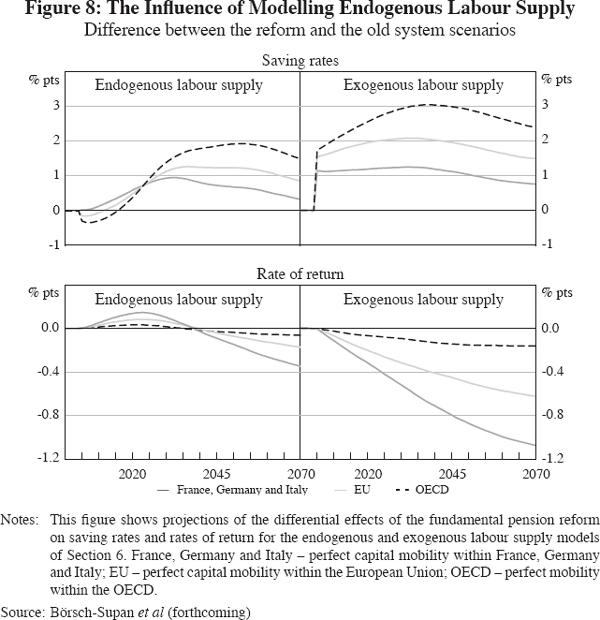
This difference in behaviour directly translates into substantial differences in the time paths of the rate of return to capital, depicted in Figure 8 (lower panel). If labour supply is endogenous, the rate of return initially increases since households increase their labour supply in response to the change in policy. This effect is absent when labour supply is exogenous. Hence, the rate of return to capital immediately decreases. As a result, the overall decrease in the rate of return to capital is much larger.
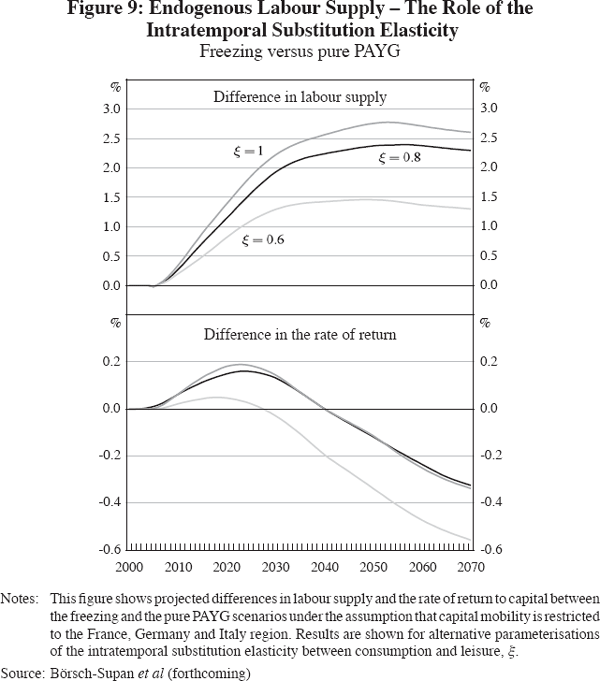
The size of this endogenous labour supply effect depends on the elasticity of substitution between consumption and leisure, ξ. This is shown in Figure 9, where we vary ξ by ± 0.2 around its benchmark value of 0.8 and re-calibrate the model such that initial labour supply shares are held constant. We focus on the case where capital mobility is restricted to the FGI region because it exhibits the strongest sensitivity (see Figure 8). In this ‘closed economy’ case, the increase of labour supply resulting from the fundamental pension reform is only slightly higher if ξ = 1 (Cobb-Douglas utility), but quite a lot lower if ξ = 0.6. As a result, the decrease in the rate of return to capital is much stronger for ξ = 0.6 than for the benchmark calibration of ξ = 0.8.
7. Econometric Estimates of Anticipated International Capital Flows
One may distrust a simulation model such as MEA-OLGA that relies entirely on the assumptions of economic theory to predict the future. This section therefore provides econometric estimates based upon past international capital flows and demographic changes. Using these estimates to project future international capital flows requires us to make some heroic assumptions: the demographic changes projected to occur in the 21st century are unprecedented in history, and there is no guarantee that relationships identified on the basis of the relatively subtle demographic changes in the past will remain stable during the huge and incisive changes likely to occur in the future.
Although not directly comparable, this section's econometric estimates support the simulations presented in the preceding sections. These estimates are based on Lührmann (2006). She uses a reduced-form approach to analyse the empirical link between current and future demographic measures and international capital flows. Her estimations are based on time-series and cross-section data for about 120 countries from 1970 to 1997. The demographic data are provided by UN Population Division (2001), while the economic data of the unbalanced panel are taken from the World Development Indicators published by the World Bank (2003). Additional data on capital controls are provided by the International Monetary Fund (1999).
The dependent variable is capital outflows, constructed as the net value of gross domestic savings minus domestic investments as a share of GDP.
Explanatory variables are regional fixed effects, present demographic measures, expected demographic changes, financial sector variables and measures of capital mobility. Regional fixed effects relate to the 18 regions identified by the United Nations. Demographic measures are the population shares of 17 age groups (0–4, 5–9, 10–14, …, 75–79, 80+) which are converted into a fourth-order polynomial by the method of Fair and Dominguez (1991). Expected demographic change employs two specifications of the effect of an increased life expectancy on these shares, described in detail by Lührmann (2006). In both specifications, past increases in life expectancies are used to project the age structure in the future. Then, youth and old-age dependency ratios are calculated at several time horizons. One specification uses as a time horizon the expected time of death for each age; a second specification uses a range of time horizons. Capital mobility and financial market influences are described by a set of variables including a dummy variable on capital controls, capital gains taxes, taxes on international trade, the size of the financial market, the ratio of private credits to GDP and the Freedom House (2002) index measuring the extent of law enforcement and property rights. Finally, financial literacy is approximated by the enrolment in secondary education.
Table 3 summarises the regression results obtained by Lührmann (2006). The coefficients of the age-structure polynomial describing current demographic measures are highly significant. If converted into marginal effects, they show that an increase in the share of the population of people who are in their most productive period of life induces net capital outflows, consistent with the intuition that these people are in their high saving years. In turn, an increase in the population share of retirees produces a net capital inflow, corresponding to the declining savings of older individuals.
| Specification 1 | Specification 2 | Specification 3 | |
|---|---|---|---|
| Present demography | |||
| D1 | −1.057 (5.73)*** | −1.171 (6.51)*** | −1.193 (5.87)*** |
| D2 | 0.312 (7.02)*** | 0.350 (7.95)*** | 0.372 (7.35)*** |
| D3 | −0.030 (7.32)*** | −0.034 (8.26)*** | −0.037 (7.89)*** |
| D4 | 0.001 (7.07)*** | 0.001 (7.99)*** | 0.001 (7.95)*** |
| Expected future demography | |||
| OLD | −0.010 (0.52) | ||
| YNG | −0.089 (4.75)*** | ||
| OLD10 | −0.083 (0.88) | ||
| OLD20 | 0.017 (0.11) | ||
| OLD30 | 0.140 (0.98) | ||
| OLD50 | −0.079 (1.52) | ||
| YNG10 | −0.240 (4.34)*** | ||
| YNG20 | 0.314 (3.47)*** | ||
| YNG30 | −0.208 (2.04)** | ||
| YNG50 | −0.089 (1.71)* | ||
| Other covariates | |||
| SIZE | −0.023 (2.05)** | −0.0248 (2.27)** | −0.0234 (2.08)** |
| TAX | 0.028 (2.35)** | 0.0216 (1.88)* | 0.0444 (3.71)*** |
| TRADETAX | −0.126 (8.36)*** | −0.1198 (8.06)*** | −0.1052 (6.66)*** |
| PRIVATE | −0.034 (4.00)*** | −0.0317 (3.80)*** | −0.0405 (4.93)*** |
| CONTROL | −0.015 (4.34)*** | −0.0162 (4.70)*** | −0.0152 (4.36)*** |
| RIGHTS | −0.003 (3.53)*** | −0.0025 (3.35)*** | −0.0020 (2.55)** |
| CIVIL | 0.002 (1.43) | 0.0014 (1.42) | 0.0022 (2.15)** |
| SCHOOL | 0.036 (3.21)*** | 0.0332 (3.01)*** | 0.0271 (2.38)** |
| CONSTANT | 0.031 (2.35)** | 0.0415 (3.37)*** | 0.0439 (2.91)*** |
| Observations | 1,823 | 1,823 | 1,802 |
|
Notes: Absolute value of z statistics in parentheses. *, ** and *** represent significance at the 10, 5 and 1 per cent levels, respectively. FGLS estimation with country-specific AR(1)-process and heteroskedasticity. Source: Lührmann (2006) |
|||
Future demographic change enters in specifications 2 and 3. A future decline in the youth dependency ratio implies a large (and statistically significant) increase in net capital outflows. Short-run effects are much larger than longer-run effects (specification 3). Lührmann attributes the insignificant old-age dependency ratios to multicollinearity with the youth dependency ratio.
Most of the financial market and capital mobility variables are significant with the expected signs. The positive effect of schooling on net capital outflows is interesting, however. High human capital levels encourage net capital outflows, probably because they raise productivity, which increases saving rates.
Figure 10 translates these regression coefficients into predicted net capital outflows (measured relative to GDP) for a selected group of countries. Clearly, all ageing countries display a similar pattern: past net capital outflows revert into net capital inflows when population ageing becomes stronger. The effect is most pronounced in Japan. China follows a generation later. Relatively youthful countries, such as India and Indonesia, have the opposite pattern. The magnitudes are large, sometimes exceeding 5 per cent of GDP.
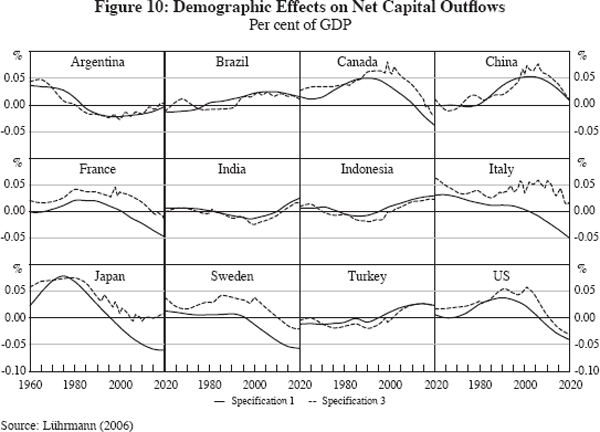
The results in this section do not fit exactly to the specification of the MEAOLGA model employed earlier. However, the patterns as well as the magnitudes correspond quite closely: capital inflows are associated with faster-ageing countries, outflows with countries that feature a less dramatic demographic change. Typical magnitudes amount to some 3–5 per cent of GDP. The broad correspondence of results obtained from such vastly different methods gives considerable confidence in the results.
8. Conclusions
Population ageing works through various mechanisms. First, demographic change alters the time path of aggregate savings within each country. Second, this process may be amplified when a pension reform, brought about in response to the demographic change, shifts old-age provision from pure PAYG systems towards systems with at least some pre-funding. Third, while the patterns of population ageing are similar in most countries, timing and initial conditions differ substantially. Hence, to the extent that capital is internationally mobile, population ageing will induce capital flows between countries.
All three effects influence the rate of return to capital and interact with the demand for capital in production and with labour supply. Our simulations predict substantial capital flows due to population ageing. Population ageing results in decreases in the capital-output ratio when baby boomers decumulate their assets. International capital flows follow this trend. The countries and regions most affected by ageing such as the European Union will initially export capital, while countries less affected by ageing like the United States and other OECD countries will import capital. This pattern reverses itself by about the year 2020 when baby boomers decumulate assets and the fast-ageing economies therefore become capital-importing regions. Pension reforms with higher degrees of pre-funding are likely to induce more capital exports during the first stage of this process. They also increase labour supply considerably, while the effects on the rate of return to capital are reduced. The results suggest that, while the rate of return to capital declines in response to population ageing, there is no devastating ‘asset-price meltdown’.
The timing of this adjustment process is complex and one has to carefully distinguish level effects from changes over time. In the initial year of our projections (2002), saving rates in the FGI region are substantially higher in the open-economy scenarios than under a closed-economy one. This reflects the higher rates of return in economies with a smaller share of older persons. Open economies are able to avoid a large proportion of the demographic effects that depress saving rates and the rate of return to capital.
This level effect is superseded by the demographic changes during the 2002 to 2070 prediction window. Saving rates decrease until 2050 across all capital mobility scenarios since the baby boom generation decumulates assets. But saving rates are projected to rebound after the year 2050. Since PAYG pension systems partially crowd out private savings, declines in saving rates are larger in the older regions (which tend to have more generous PAYG pension systems). As a result, in a closed-economy setting, the decrease in the rate of return would be lower in these regions than in regions with less generous pension systems. The advantages of worldwide capital mobility are therefore not as great for countries with generous PAYG pension systems. We should stress that population projections are reliable one generation ahead, while the projection error increases substantially thereafter. Consequently, results for the post-2030 period should be interpreted with care.
We presented econometric results from a panel of national time series in which saving rates, rates of return and international capital flows are related to anticipated demographic change. These estimates support the results from the multi-country OLG model.
Finally, this paper shows the importance of the interplay between saving and labour supply adjustments in response to population ageing. Saving rates, rates of return and international capital flows react substantially less to demographic change once households absorb some part of the demographic shock by working more.
Footnotes
This paper rests on work done by several researchers at the Mannheim Research Institute
(MEA). The overlapping generations model has been developed by Alexander
Ludwig. The econometric work was part of Melanie Lührmann's dissertation.
The work on asset-price meltdowns has been done by Mathias Sommer. Joachim
Winter has helped me a great deal in supervising this work. My primary thanks
go to these dedicated MEA researchers.
We thank Alan Auerbach, Ralph Bryant, Hans Fehr, Alexia Fürnkranz-Prskawetz,
Ulrich Grosch, Florian Heiss,
Heinz Hermann, Gary Hufbauer, Ulf von Kalkreuth, Florence Legros, Shinichi Nishiyama,
Howard Rosen and Tarmo Valkonen for their helpful remarks on this line of
research, and Holger Herz and Max Flötotto for their excellent research
assistance. We also received helpful feedback at many conferences and seminars.
This ongoing project is supported by the VW Foundation, the Deutsche Forschungsgemeinschaft,
the Land of Baden Württemberg, the Gesamtverband der deutschen Versicherungswirtschaft,
and the US Social Security Administration through grant #10-P-98363-2 to
the National Bureau of Economic Research as part of the SSA Retirement Research
Consortium. The findings and conclusions expressed are solely those of the
author and do not represent the views of SSA, any agency of the US Government,
or the NBER.
[1]
See Obstfeld and Rogoff (1996) and Coakley, Kulasi and Smith (1998) for surveys of the literature. [2]
Rising until the age of 55 and then constant. [3]
See Börsch-Supan et al (2003) for a description of these. [4]
More precisely, it is the marginal productivity of capital deployed per efficiency
unit of work, 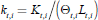 . The depreciation
rate δ is assumed to be constant and uniform across countries.
[5]
. The depreciation
rate δ is assumed to be constant and uniform across countries.
[5]
Population data for 1950–2050 are given at an annual frequency for five-year age groups. Further input data such as age-specific mortality rates, life expectancy and aggregate migration are only provided at quinquennial frequency. We interpolate between age groups and time intervals and ‘backfit’ our population model to the UN population data for the time period 1950–2050. [6]
Since there is no government consumption in the model, we define output as the difference between actual GDP and government consumption. [7]
We choose this scenario as our benchmark for two reasons. First, as noted in Section 2, there is a broad consensus that capital mobility is greater among OECD countries than it is between developed and developing countries. Second, adding the additional countries of the ‘rest of the world’ region does not substantially affect patterns of aggregate variables because roughly 80 per cent of world GDP is produced in the OECD. [8]
The total sum of pensioners (‘effective pensioners’) as used in this section is defined as the sum of actual pensioners weighted by their age-specific pension entitlements. [9]
We provide such standard sensitivity analysis in Börsch-Supan et al (2004). [10]
References
Abel AB (2001), ‘Will Bequests Attenuate the Predicted Meltdown in Stock Prices When Baby Boomers Retire?’, Review of Economics and Statistics, 83(4), pp 589–595.
Abel AB (2003), ‘The Effects of a Baby Boom on Stock Prices and Capital Accumulation in the Presence of Social Security’, Econometrica, 71(2), pp 551–578.
Altig DE, AJ Auerbach, LJ Kotlikoff, KA Smetters and J Walliser (2001), ‘Simulating Fundamental Tax Reform in the United States’, American Economic Review, 91(3), pp 574–595.
Ando A and F Modigliani (1963), ‘The ‘Life-Cycle’ Hypothesis of Saving: Aggregate Implications and Tests’, American Economic Review, 53(1), Part 1, pp 55–84.
Auerbach AJ and LJ Kotlikoff (1987), Dynamic Fiscal Policy, Cambridge University Press, Cambridge.
Baxter M and MJ Crucini (1993), ‘Explaining Saving-Investment Correlations’, American Economic Review, 83(3), pp 416–436.
Bloom DE and JG Williamson (1998), ‘Demographic Transitions and Economic Miracles in Emerging Asia’, World Bank Economic Review, 12(3), pp 419–455.
Börsch-Supan AH, A Ludwig and M Sommer (2003), Demographie und Kapitalmärkte – Die Auswirkungen der Bevölkerungsalterung auf Aktien-. Renten- und Immobilienvermögen, Deutsches Institut für Altersvorsorge, Köln.
Börsch-Supan AH, A Ludwig and JK Winter (2002), ‘Aging, Pension Reform , and Capital Flows’, in AJ Auerbach and H Hermann (eds), Aging, Financial Markets and Monetary Policy, Springer, Heidelberg, pp 55–83.
Börsch-Supan AH, A Ludwig and JK Winter (2004), ‘Aging, Pension Reform, and Capital Flows: A Multi-Country Simulation Model’, University of Mannheim Discussion Paper No 04-64.
Börsch-Supan AH, A Ludwig and JK Winter (forthcoming), ‘Aging, Pension Reform, and Capital Flows: A Multi-Country Simulation Model’, Economica.
Brooks R (2002), ‘Asset-Market Effects of the Baby Boom and Social-Security Reform’, American Economic Review, Papers and Proceedings, 92(2), pp 402–406.
Brooks R (2003), ‘Population Aging and Global Capital Flows in a Parallel Universe’, IMF Staff Papers, 50(2), pp 200–221.
Coakley J, F Kulasi and R Smith (1998), ‘The Feldstein-Horioka Puzzle and Capital Mobility: A Review’, International Journal of Finance and Economics, 3(2), pp 169–188.
Cutler DM, JM Poterba, LM Sheiner and LH Summers (1990), ‘An Aging Society: Opportunity or Challenge?’, Brookings Papers on Economic Activity, 1, pp 1–73.
Deardorff AV (1987), ‘Trade and Capital Mobility in a World of Diverging Populations’, in DG Johnson and RD Lee (eds), Population Growth and Economic Development: Issues and Evidence, University of Wisconsin Press, Madison, pp 561–588.
Diamond PA (1965), ‘National Debt in a Neoclassical Growth Model’, American Economic Review, 55(5), pp 1126–1150.
Domeij D and M Flodén (2006), ‘Population Aging and International Capital Flows’, International Economic Review, 47(3), pp 1013–1032.
Engelhardt GV and JM Poterba (1991), ‘House Prices and Demographic Change – Canadian Evidence’, Regional Science and Urban Economics, 21(4), pp 539–546.
Fair RC and KM Dominguez (1991), ‘Effects of the Changing U.S. Age Distribution on Macroeconomic Equations’, American Economic Review, 81(5), pp 1276–1294.
Feldstein M and C Horioka (1980), ‘Domestic Saving and International Capital Flows’, Economic Journal, 90, pp 314–329.
Feroli M (2003), ‘Capital Flows among the G-7 Nations: A Demographic Perspective’, Federal Reserve System Finance and Economics Discussion Series No 2003/54.
Fitzenberger B, R Hujer, TE MaCurdy and R Schnabel (2001), ‘Testing for Uniform Wage Trends in West-Germany: A Cohort Analysis Using Quantile Regressions for Censored Data’, Empirical Economics, 26(1), pp 41–86.
Freedom House (2002), Freedom in the World: The Annual Survey of Political Rights and Civil Liberties, Freedom House, New York.
French KR and JM Poterba (1991), ‘Investor Diversification and International Equity Markets’, American Economic Review, Papers and Proceedings, 81(2), pp 222–226.
Hamilton BW (1991), ‘The Baby Boom, the Baby Bust, and the Housing Market – A Second Look’, Regional Science and Urban Economics, 21(4), pp 547–552.
Hendershott PH (1991), ‘Are Real House Prices Likely to Decline by 47 Percent?’, Regional Science and Urban Economics, 21(4), pp 553–563.
Henriksen E (2002), ‘A Demographic Explanation of U.S. and Japanese Current Account Behavior’, Carnegie Mellon University, unpublished manuscript.
Higgins M (1998), ‘Demography, National Savings, and International Capital Flows’, International Economic Review, 39(2), pp 343–369.
Hurd MD (1989), ‘Mortality Risk and Bequests’, Econometrica, 57(4), pp 779–813.
IMF (International Monetary Fund) (1999), Annual Report on Exchange Arrangements and Exchange Restrictions, IMF, Washington DC.
Lührmann M (2006), ‘Demographic Change, Foresight and International Capital Flows’, Mannheim Research Institute for the Economics of Aging (MEA) Discussion Paper No 38-2003.
Mankiw GN and DN Weil (1989), ‘The Baby Boom, the Baby Bust, and the Housing Market’, Regional Science and Urban Economics, 19(2), pp 235–258.
Mankiw GN and DN Weil (1992), ‘The Baby Boom, the Baby Bust, and the Housing Market – A Reply to Our Critics’, Regional Science and Urban Economics, 21(4), pp 573–579.
McFadden D (1994), ‘Demographics, the Housing Market, and the Welfare of the Elderly’, in DA Wise (ed), Studies in the Economics of Aging, University of Chicago Press, Chicago, pp 225–290.
Modigliani F and R Brumberg (1954), ‘Utility Analysis and the Consumption Function: An Interpretation of Cross-Section Data’, in KK Kurihara (ed), Post-Keynesian Economics, Rutgers University Press, New Brunswick, pp 388–436.
Obstfeld M (1986), ‘Capital Mobility in the World Economy: Theory and Measurement’, Carnegie-Rochester Conference Series on Public Policy, 24, pp 55–103.
Obstfeld M and K Rogoff (1996), Foundations of International Macroeconomics, MIT Press, Cambridge.
Obstfeld M and K Rogoff (2001), ‘The Six Major Puzzles in International Macroeconomics: Is There a Common Cause?’, NBER Macroeconomics Annual 2000, 15, pp 339–390.
OECD (2001), Taxing Wages 2000–2001, OECD, Paris.
OECD (2004), STAN Database, 2003 edn, OECD, Paris.
Palacios R and M Pallarès-Miralles (2000), ‘International Patterns of Pension Provision’, World Bank Social Protection Discussion Paper Series No 0009.
Pemberton J (1999), ‘Social Security: National Policies with International Implications’, Economic Journal, 109(457), pp 492–508.
Portes R and H Rey (2005), ‘The Determinants of Cross-Border Equity Flows’, Journal of International Economics, 65(2), pp 269–296.
Poterba JM (2001), ‘Demographic Structure and Assets Returns’, Review of Economics and Statistics, 83(4), pp 565–584.
Reisen H (2000), Pensions, Savings and Capital Flows: From Aging to Emerging Markets, Edward Elgar, Cheltenham.
Samuelson PA (1958), ‘An Exact Consumption-Loan Model of Interest with or without the Social Contrivance of Money’, Journal of Political Economy, 66(6), pp 467–482.
Skinner, J (1996), ‘Is Housing Wealth a Sideshow?’ in DA Wise (ed.), Advances in the Economics of Aging, University of Chicago Press, Chicago, pp 241–274.
Swan C (1995), ‘Demography and the Demand for Housing: A Reinterpretation of the Mankiw-Weil Demand Variable’, Regional Science and Urban Economics, 25(1), pp 41–58.
Taylor AM (1994), ‘Domestic Saving and International Capital Flows Reconsidered’, NBER Working Paper No 4892.
UN Population Division (2001), World Population Prospects: The 2000 Revision, United Nations, New York.
Venti SF and DA Wise (1990), ‘Have IRAs Increased U.S. Saving? Evidence from Consumer Expenditure Surveys’, The Quarterly Journal of Economics, 105(3), pp 661–698.
Woodward SE (1991), ‘Economists' Prejudices: Why the Mankiw-Weil Story is Not Credible’, Regional Science and Urban Economics, 21(4), pp 531–537.
World Bank (2003): World Development Indicators, World Bank, Washington DC.