RBA Annual Conference – 2006 Demographic Change and Asset Prices Robin Brooks[1]
Abstract
Will the ageing of the baby boomers lead to a financial market meltdown? Will population ageing raise the equity premium, as ageing households become less willing to bear risk? This paper investigates these questions, using a new dataset that covers stock and bond prices, as well as age distributions, for a large cross-section of developed countries from the early 1900s. It uses an econometric specification that links real stock and bond prices, real returns and the equity premium to the relative importance of all age groups in the age distribution. It finds little evidence to suggest that asset prices will suffer abrupt declines when the baby boomers retire. In fact, in countries where stock market participation is greatest, including Australia, Canada, New Zealand, the United Kingdom and the United States, evidence suggests that real financial asset prices may continue to rise as populations age, consistent with survey evidence that households continue to accumulate financial wealth well into old age and do little to run down their savings in retirement.
1. Introduction
When it comes to predicting the effects of population ageing on financial markets, there are two camps: those who believe in the doomsday scenario – the market meltdown – and those who do not. The meltdown scenario holds that retiring baby boomers will be selling their assets to a smaller generation of young investors. This will drive asset prices down, leaving many baby boomers with a smaller nest-egg than anticipated. The opposing view maintains that forward-looking financial markets are pricing assets to reflect the highly predictable ageing of the baby boomer generation. As a result, there cannot be a market meltdown when the baby boomers retire, because it has already been priced in.
The ageing of the baby boomers and speculation over the possible effects on financial markets has raised the profile of this issue, both in the financial press and in academic circles.[2] Indeed, a recent convert to the asset-price meltdown camp, Wharton Business School Professor Jeremy Siegel, has done much to enliven the debate, by claiming that baby boomers across the industrialised world may see the value of their accumulated assets – stocks, bonds and homes – plunge by up to 50 per cent over their remaining life span, as they try to unload their assets on a smaller generation of buyers. In a forthcoming book, The Global Solution, Siegel warns that the only way to forestall this meltdown is to allow retiring baby boomers to sell their assets to Chinese and Indian investors, whose soaring economies will make them net buyers in coming decades.
But will the asset-price meltdown happen? A casual case for the meltdown scenario can easily be made. Figure 1 shows a real US stock price index (S&P 500) and the ratio of the US population aged 40–64 relative to the rest of the population (those aged 0–39 and 65+) from 1950 to 2050, using population projections from the United Nations. This demonstrates that the decline in real stock prices during the 1970s and early 1980s coincided with a fall in the relative importance of those aged 40–64, as large ranks of baby boomers (defined as the 78.2 million people in the US born between 1946–1964) entered the population and pulled down this population ratio. Proponents of the meltdown scenario argue that the fall in the proportion of the population aged 40–64 caused a decline in the demand for stocks, as the parents of the baby boomer generation shifted their focus to buying houses and raising their children, which in turn depressed real stock prices. As the baby boomer generation aged and moved into its prime saving years, typically defined as between ages 40–64, the demand for stocks rose, pushing up real stock prices. Proponents of the asset-price meltdown scenario thus see the stock market rally of the late 1990s as resulting from the ageing of the baby boomer generation.
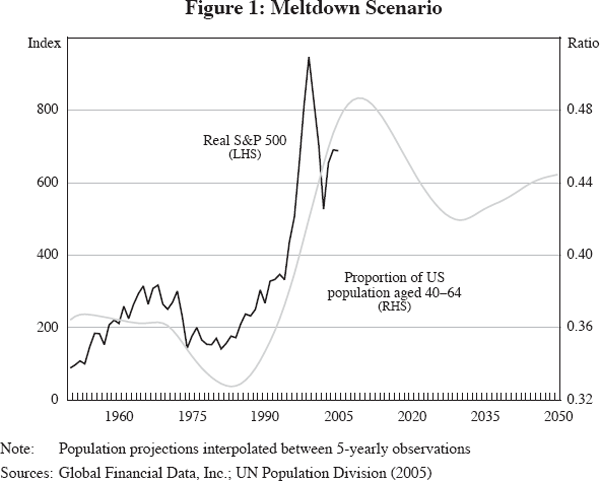
As compelling as Figure 1 may be, there are several problems with interpreting it as a predictor of a future asset-price meltdown. First, since its peak in 2000, the stock market has fallen 30 per cent in real terms and much of the run-up in the late 1990s is now seen – with the benefit of hindsight – as a stock market bubble, fuelled by unrealistic expectations about the effects of information technology on profits. Of course, the stock market has not reversed all gains since the late 1990s, leaving open the possibility that demographics is a factor behind some of the sustained increase since then. Second, Figure 1 paints a deceptive picture, because it omits other factors that may have driven both demographics and the stock market. A prime candidate is a long-run cycle in economic activity, driven for example by global events such as World War II. The war may have caused US fertility rates to fall and also depressed real stock prices, due in part to the greater uncertainty at the time. The end of World War II saw a dramatic recovery in economic activity around the world, causing the stock market to soar, while better economic prospects led to a rebound in fertility rates. Economic prospects suffered again in the 1970s and 1980s, as a series of oil shocks pushed up inflation, forced policy-makers to slow economic growth, and sent stock markets plunging in real terms. At around this time, fertility rates fell dramatically around the world, driven by increased labour force participation rates among women and the introduction of ‘the pill’. In other words, the empirical association between the two series in Figure 1 may not reflect a causal relationship, but simply an omitted factor. Third, the effective number of observations in Figure 1 is too small to draw a decisive conclusion on the link between demographics and financial markets. While such a link may well exist, it is impossible to identify on the basis of ‘one’ baby boom. Given these concerns, it may not be so surprising that the academic literature has failed to identify a strong link between demographics and financial markets, suggesting that Figure 1 needs to be interpreted with caution.
Against this background, this paper revisits the debate over whether there is a link between demographics and financial markets. It makes two important advances over the existing literature. First, it constructs a new dataset for developed economies that contains a long time series on stock and bond prices, as well as age distributions. The long time-series dimension of the data (most of the data start between 1900 and 1925) increases the number of effective observations, and helps to clarify the impacts of demographic changes, which typically occur only at low frequencies. Second, it employs a new empirical specification which links real asset prices, real returns and the equity premium to the entire age distribution, effectively deriving the sensitivity of financial markets with respect to all age groups. Compared to the existing literature, which predominantly uses ratios such as the relative importance of those aged 40–64, this approach has the advantage of avoiding an ad hoc partition of the age distribution into those more likely to save and those less likely to save.
This paper does not find a strong historical link between demographics and financial markets. While the existing literature has found that the relative importance of middle-aged cohorts tends to be associated with high real stock and bond prices, this paper shows that this association does not hold for countries with strong equity market participation among households, such as Australia, Canada, New Zealand, the UK and the US. In these countries, higher real financial asset prices tend to be associated with an increase in the proportion of the population in the old tail of the age distribution. This is consistent with survey evidence from the US that shows that households run up financial wealth well into old age and then do little to run it down in retirement. Taken at face value, this suggests that real financial asset prices in the US will actually rise as the population continues to age, though a number of considerations – including the changing nature of markets over time and general equilibrium effects – caution against drawing this conclusion. Nonetheless, this finding underscores that historical evidence provides little support for the hypothesis that financial market prices will fall abruptly when the baby boomers retire.
The remainder of this paper is structured as follows. Section 2 reviews the existing theoretical literature on the link between demographics and financial markets. Section 3 reviews existing empirical work. Section 4 describes the data used in this paper, while Section 5 describes the estimation approach. Section 6 discusses the results. Section 7 concludes.
2. Existing Theoretical Work on Demographics and Financial Markets
A number of papers have calibrated numerical intertemporal general equilibrium models to simulate the effects of demographic dynamics on asset prices and returns. Yoo (1994a) uses an overlapping generations (OLG) model in which agents live for 55 periods and work for 45. For a simulated baby boom that is calibrated to match the experience of the US over the last four decades, Yoo finds that the return to capital may fall by up to 40 basis points when the boomers shift into retirement, consistent with the claim that baby boomers may face lower financial market returns over their lifetime. Brooks (2002) also uses an OLG model to simulate the effects of demographic dynamics on stock and bond returns. Agents in Brooks' model live for four periods: childhood, young working age, old working age and retirement. In childhood, agents are not independent decision-makers and depend on their parents for consumption. In the two middle periods, agents supply labour inelastically and save for retirement, investing in either risky capital or safe bonds. In retirement, they run down their savings, there being no bequests. Brooks simulates a baby boom and bust that is calibrated to match the US experience and finds that demographic dynamics have a small effect on the return to capital, but a larger effect on the risk-free rate, as ageing boomers crowd into safe bonds as they approach retirement, in order to reduce consumption risk. This pushes down the risk-free rate relative to the return to capital, though the overall effect – in the order of 50 basis points – is still modest in size. Abel (2001, 2003) derives analytical results based on an OLG model. He shows that a stylised baby boom, in which the birth rate first rises and then falls, reduces the rate of return relative to what it would be in the absence of population changes. He concludes that baby boomers face less attractive capital market opportunities than smaller cohorts around them, a conclusion that is also derived analytically by Bohn (2001). Geanakoplos, Magill and Quinzii (2004) use an OLG model that is closely calibrated to match the US, including realistic age-income patterns. Their findings suggest that demographic shocks like those experienced in the post-WW II US could generate substantial swings in asset values, but that actual peak-to-trough movements in the stock market are two to three times greater than the demographic analysis can explain.
These papers are subject to several important caveats. First, they all assume that the life-cycle hypothesis of Modigliani and Brumberg (1954) holds, whereby agents smooth consumption over their life spans. This implies a profile of wealth that rises until retirement and subsequently falls, as agents run down their assets to fund consumption. However, household survey data from the US suggest that actual savings behaviour does not conform well to this pattern. In particular, there is little evidence that households dissave dramatically in retirement. As Figure 2 shows, net financial wealth according to the 2001 Survey of Consumer Finances peaks between the ages of 55–59, but declines very little thereafter. This lack of evidence to support the life-cycle hypothesis could reflect a number of factors. Precautionary saving may rise as households age, as the need to self-insure against medical emergencies rises. It is also possible that the cross-sectional nature of the Survey of Consumer Finances gives a distorted picture, as it lumps together households of different ages. For example, it is possible that people born during the Great Depression are more risk averse than young people of today. In a simple cross-section, this could give the distorted picture that wealth rises with age, when in fact this finding merely reflects different risk preferences. However, attempts to control for such cohort effects, by Poterba (2001) and others, yield little change in estimated age-wealth profiles, suggesting that such effects are small.
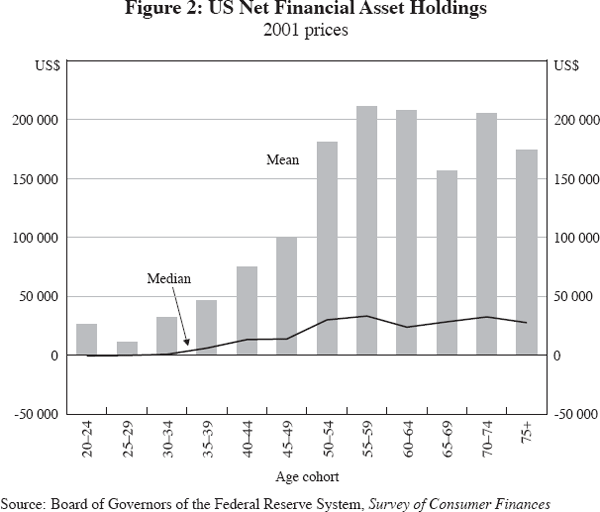
Second, existing efforts to model the impact of demographics on financial markets typically assume a representative agent within each cohort, when in fact holdings of financial assets are skewed towards the very rich. Figure 2 provides an indication of this. It shows that median net financial wealth is substantially lower across all age groups than mean net financial wealth. Indeed, with median net financial wealth so low in the US, Figure 2 suggests that a substantial number of households do not have significant holdings of financial assets at all. With the exception of Storesletten, Telmer and Yaron (2004), the high degree of heterogeneity across households within age groups has largely been ignored.
Third, the existing literature tends to work within the confines of closed-economy models, which preclude agents from diversifying away demographic risk by investing in countries with different demographic profiles. Attanasio and Violante (2000), Börsch-Supan, Ludwig and Winter (2005), Brooks (2003) and others have used OLG models to simulate the effects of differential demographic trends around the world on saving-investment balances. Though these papers suggest that international capital flows will tend to attenuate any adverse effects of population ageing on financial markets, they fail to match the historical pattern of capital flows (the global imbalances conundrum), raising the question as to the relevance of such approaches.
In summary, the existing theoretical literature suggests that the baby boomers will earn returns on their retirement savings that will be below the historical norm, but that any adverse effects will be small and may be swamped by other sources of volatility. In particular, important shortcomings of these models suggest that any simulated effects should be treated as upper bounds, given that they are generated in models that assume dissaving in retirement, a representative investor in each age group, and a closed economy.
3. Existing Empirical Work on Demographics and Financial Markets
Several papers have studied the empirical link between demographic change and asset prices. Yoo (1994b) regresses real returns on stocks, bonds and Treasury bills in the US on various measures of the age distribution that aim to proxy for demand for financial assets (similar to that used in Figure 1). For Treasury bills he finds a significant relationship, whereby a higher fraction of the population in their prime saving years is associated with a lower real return, while large standard errors make it hard to draw any firm inferences about the link between demographics and stock and bond returns. Bergantino (1998) uses cross-sectional data from the Survey of Consumer Finances to estimate age-specific demands for corporate stock and owner-occupied real estate, and combines these estimates with data on the changing age composition of the population to create measures of aggregate demand for both equities and housing. He finds a positive association between his measure of asset demand and the level of stock prices and concludes that demographic changes can explain a substantial share of the post-war fluctuations in equity prices. Brooks (1998) exploits cross-country variation by relating the level of real equity prices to the relative importance of the population aged 40–64. For 11 of the 14 countries in his sample, there is a positive relationship between this demographic variable and the real stock price. Poterba (2001) builds on these studies and re-examines the relationship between several measures of demographic structure and real returns on Treasury bills, government bonds and equities. As in Yoo (1994b), there is weak evidence linking the population age structure to real returns on Treasury bills, but little other evidence. Poterba notes, however, that there is some evidence of a link between price-dividend ratios and demographic variables, suggesting that perhaps the volatility of returns data tends to obscure a possible link to a low frequency source of variation such as demographics. Davis and Li (2003) focus on a smaller sample of seven countries with substantial equity markets. They find a statistically significant effect of the share of the population aged of 40–64 on the level of real stock and bond prices. Their finding is robust to the inclusion of variables that control for non-demographic factors that may affect asset prices, such as the rate of economic growth and inflation. Geanakoplos et al (2004) present empirical evidence consistent with their own simulation analysis (described earlier). Their results suggest that the real level of share prices, measured by the S&P 500 index, is related to the ratio of middle-aged to young individuals in the population. This ‘MY ratio’ is defined as the number of 40–49 year olds divided by the number of 20–29-year olds. The results suggest a statistically significant link between the MY ratio and real stock returns, with a change like that projected for the 2000–2050 period resulting in roughly a 60 basis point decline in annual real returns. They also study France, Germany, Japan and the UK, and find mixed results. For France and Japan there appears to be a link between the MY ratio and the real price of corporate equities, but the relationship does not emerge in the other economies.
The empirical literature thus finds some evidence of a link between demographics and financial markets, though the estimated effects are small, consistent with the theoretical literature. A particular curse that bedevils the empirical literature is that the effective number of observations is small. As Poterba (2004a, p 13) puts it: ‘Since there is only one Baby Boom in the United States, it may be misleading to suggest that there are many years of data on demographics and asset market returns. It may be more accurate to view the existing data as the result of one realization of time-varying birth rates’. This paper attempts to address this problem by extending data back to the early 1900s, while much of the existing literature has focused on the post-war period.
4. Data Description
This paper constructs a new dataset that contains a long time-series on stock and bond prices, as well as age distributions, across advanced countries. The long time-series dimension of the data (most of the data start between 1900 and 1925) aims to increase the effective number of observations in light of the slow-moving nature of demographic change.
Table 1 summarises the composition of the data across countries and over time. For each country there is a stock price index, a total return index for the stock market (which differs from the stock price index because it assumes that dividends are reinvested), a total return bond index, a total return Treasury bill index, a consumer price index and age distribution data, which describe the number of people in 5-year age groups (0–4, 5–9, …, 75+). All data are available at an annual frequency. Data for the US are available from 1900 onwards, while the majority of countries join the sample between 1910 and 1925. In the case of Germany and Italy, the lack of demographic data for the pre-war period means that data are only available from 1950.
| Start date | End date | |
|---|---|---|
| Australia | 1921 | 2005 |
| Belgium | 1920 | 2005 |
| Canada | 1921 | 2005 |
| Denmark | 1915 | 2005 |
| Finland | 1922 | 2005 |
| France | 1921 | 2005 |
| Germany | 1950 | 2005 |
| Italy | 1950 | 2005 |
| Japan | 1920 | 2005 |
| Netherlands | 1901 | 2005 |
| NZ | 1926 | 2005 |
| Norway | 1918 | 2005 |
| Sweden | 1921 | 2005 |
| Switzerland | 1921 | 2005 |
| UK | 1911 | 2005 |
| US | 1900 | 2005 |
| Notes: Financial data are from <www.globalfinancialdata.com>. Population data are from the statistical agency of each country and from UN Population Division (2005), which includes population projections out to 2050. Projections are based on the medium variant. | ||
Table 2 summarises projected ageing trends in the sample countries, showing the old-age dependency ratio, which is calculated as the number of people aged 65 and older relative to the number of people aged between 20–64. As is well known, population ageing is projected to be most severe in Japan, where the old-age dependency ratio is forecast to rise by 50 percentage points to 78 per cent by 2050. Population ageing is also projected to be severe in Italy, where the orders of magnitude are similar. In contrast, population ageing in the US is projected to be relatively benign, with the old-age dependency ratio forecast to rise from 21 per cent in 2000 to 37 per cent by 2050. Ageing trends are similarly restrained in the UK, although its population is already older than the US population.
| 2000 | 2010 | 2020 | 2030 | 2040 | 2050 | |
|---|---|---|---|---|---|---|
| Australia | 20.4 | 22.3 | 29.0 | 36.5 | 41.0 | 43.5 |
| Belgium | 28.3 | 29.7 | 35.9 | 45.6 | 51.6 | 52.1 |
| Canada | 20.5 | 22.5 | 30.2 | 41.5 | 45.9 | 48.2 |
| Denmark | 24.1 | 27.7 | 33.7 | 39.2 | 44.2 | 41.7 |
| Finland | 24.7 | 28.4 | 40.0 | 48.1 | 49.2 | 50.4 |
| France | 27.9 | 28.5 | 37.1 | 44.9 | 50.5 | 52.4 |
| Germany | 26.3 | 33.5 | 36.7 | 48.4 | 55.9 | 55.0 |
| Italy | 29.3 | 35.0 | 42.1 | 53.3 | 71.2 | 75.9 |
| Japan | 27.6 | 38.0 | 51.6 | 56.8 | 69.5 | 77.8 |
| Netherlands | 21.9 | 24.6 | 32.8 | 42.4 | 49.9 | 47.6 |
| NZ | 20.4 | 22.1 | 28.6 | 37.8 | 42.4 | 43.2 |
| Norway | 26.1 | 26.5 | 32.9 | 39.8 | 46.4 | 45.3 |
| Sweden | 29.5 | 31.7 | 37.9 | 42.6 | 46.5 | 46.0 |
| Switzerland | 24.3 | 29.2 | 36.3 | 48.8 | 55.6 | 53.8 |
| UK | 26.9 | 27.4 | 31.8 | 38.4 | 42.7 | 42.3 |
| US | 20.9 | 21.3 | 27.1 | 34.2 | 35.9 | 36.8 |
|
Source: UN Population Division (2005) |
||||||
Although the data have a significant cross-country dimension, there are important caveats. First, especially with respect to the demographic data, it is important to recognise that fertility and longevity trends in advanced countries have to a large extent been driven by common shocks, such as World War II and the post-war recovery. As such, the cross-country data are not independent observations, though there is of course country-specific variation in the data. Second, it may be misleading to link asset prices to domestic age distribution data in small open economies such as Belgium, Denmark and the Netherlands. This is because such countries now have a substantial share of foreign investors in their equity markets, so that it is unclear whether domestic demographic variables should have much impact on asset returns and asset values. Though this is certainly a consideration, one advantage of the long time-series data assembled here is that international capital flows were negligible for much of the sample period under study.
5. Empirical Specification
This section outlines an empirical specification that uses the cross-section dimension of the data to control for a global, long-run business cycle, reflecting the possible impact of events such as the Great Depression, World War II and the oil shocks in the 1970s and 1980s on financial markets and demographic developments. As the introduction argued, omitting such a cycle could result in spurious regression results, due to omitted variable bias. An alternative approach would be to follow Davis and Li (2003) who explicitly control for non-demographic fundamentals. In addition, the specification allows the entire age distribution to enter, unlike the existing literature which relies on standard demographic ratios such as the relative importance of the population aged 40–64. As noted above, such ratios have the disadvantage that they arbitrarily partition the age distribution into net savers and net dissavers, while the approach employed here takes a more agnostic approach and lets the data speak for themselves. The regression model can be written as:
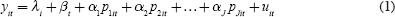
where i = 1, …, N and t = 1, …, T index the cross-section and time-series dimensions of the data. yit is the dependent variable, which could be real stock prices, real stock returns or the equity premium. λi is a country dummy; while βt is a time dummy, which controls for the global cycle discussed above; and p1it, p2it, …, pJit represent shares of the population in the J age groups as a fraction of the total population. Constraining the coefficients on the age shares to lie along a third-order polynomial (for example) means that they are constructed as:

The αj must be restricted to sum to zero because the population shares sum to unity, and are thus collinear with the country and time dummies. Imposing the restrictions, Equation (1) can be rewritten as:
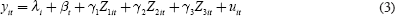
where

Constraining the αjs in this way means that there are only three independent population coefficients to estimate (γ1, γ2 and γ3). Although these coefficients have no direct structural interpretation, the implicit age distribution coefficients can easily be recovered and will capture the sensitivity of asset prices, returns and the equity premium to the age distribution.
Equation (3) is estimated by OLS. Likelihood ratio tests are performed to test for the appropriate polynomial order for the population shares. Estimation is on an unbalanced panel, to take advantage of the maximum amount of data across countries. To enable an easier comparison with the existing literature, estimations are also performed using conventional demographic variables. These are defined as shares of the total population (in per cent) accounted for by: people aged 0–14 (RAT0); people aged 15–39 (RAT15); people aged 40–64 (RAT40); and people aged 65+ (RAT65). Also included are the share of the adult (aged 20+) population aged 40–64 (RAT4020); the share of the adult population aged 65+ (RAT6520); and the average age of the adult population (AA20).
The first two of these variables capture the younger tail of the age distribution and are intended to explore the effects of changes in youth dependency on financial markets. Variations of the second two variables have been widely used in the existing literature, including in Brooks (1998), Poterba (2001, 2004a, 2004b) and Davis and Li (2003), to describe the importance of middle-aged and old cohorts in the population. The next two measures were used in Poterba (2004a, 2004b) to capture the relative importance of middle-aged and old cohorts in the adult population, while the last measure was proposed by Bakshi and Chen (1994) to describe the ageing of the adult population.
6. Results
Theoretical models, including those discussed above, show that when a large middle-aged cohort begins to purchase assets for retirement, it bids up asset prices. This implies both a positive return when this occurs, and a positive association between the level of asset prices and the relative importance of middle-aged cohorts in the age distribution. As a result, the existing empirical literature has focused on both asset prices and returns in its investigation of the financial market effects of demographic change. The advantage of looking at asset prices, rather than returns, is that they do not exhibit the same amount of volatility, which may obscure the ability to observe a link to slow-moving demographic change. The disadvantage is that both asset prices and demographics exhibit a high degree of persistence, raising the possibility that unit roots in both explanatory and dependent variables may bedevil the results. This paper uses both returns and asset prices to investigate a possible link between demographics and financial markets, with the understanding that regressions based on asset prices are likely to overstate the link, while data on returns are prone to understate it.
6.1 Asset prices and demographics
This section explores the link between demographics and real stock prices, real total return stock indices, real total return bond indices and real total return Treasury bill indices. The reason for looking at both stock prices and a total return stock index is that the former focuses on supply-demand mismatches that may result from demographic change, causing stock prices to rise or fall, while the latter focuses on the total return on equity, which better corresponds to the return to capital that is the focus of much of the theoretical literature.
This section begins by estimating a pooled version of Equation (3), where γ1, γ2 and γ3 are constrained to be the same across the 16 countries in the sample. The implicit assumption is that the link between financial markets and demographics is the same across the 16 countries in the sample. Figure 3 shows the age coefficients (α's) for a third-order polynomial for real stock prices, real total return stock indices, real total return bond indices and real total return Treasury bill indices (all of which are normalised to 100 in 2005); error bands of two standard deviations on either side are also shown.[3] Regressions are performed separately for each financial asset price series. Across all series, a clear pattern stands out: having a large proportion of the population in the younger parts of the age distribution (between 10–14 and 30–34) tends to be associated with significantly lower real stock, bond and Treasury bill prices, while large proportions of the total population in middle-aged cohorts (between 40–44 and 60–64) tend to be associated with significantly higher real financial asset prices. Finally, a large share of very old age groups tend to be associated with sharply lower real stock, bond and Treasury bill prices, consistent with the notion that older households run down their financial asset holdings in retirement, while very young age groups are associated with high real financial asset prices, possibly because parents are saving for housing or education. This finding has intuitive appeal as it suggests that middle-aged households accumulate financial wealth, only to decumulate it in retirement.
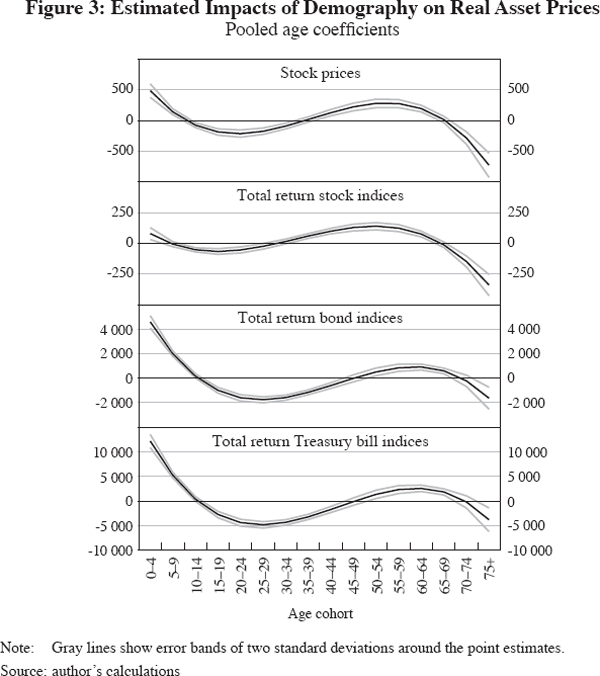
But what about relative stock and bond prices? Is there evidence that households shift their portfolio of financial assets from risky equity to less risky assets (such as Treasury bills) as they age? Figure 4 investigates this possibility, and finds that the relative price of stocks relative to Treasury bills falls as the importance of very old cohorts in the population grows. This pattern is also evident for the total returns for stocks relative to Treasury bills and for the relative price of bonds to Treasury bills.
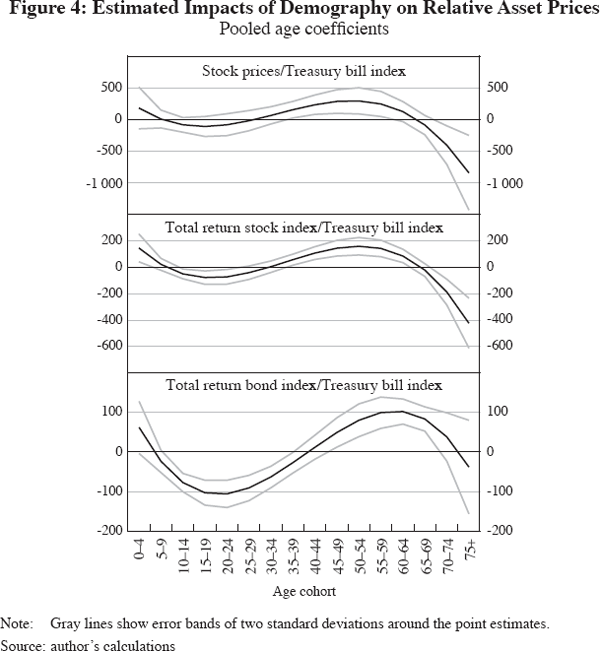
These results are in line with regressions that use conventional demographic variables. Table A1 in the Appendix reports on regressions based on Equation (3) where the polynomial specification in the age distribution is replaced with the conventional set of demographic variables outlined above. It shows that the RAT40 variable is significantly and positively related to real stock prices and real total return stock indices, while the RAT65 variable is negatively and significantly related to real equity prices. In contrast, real bond and Treasury bill prices are negatively and significantly related to the RAT40 variable, while real Treasury bill prices are positively related to the RAT65 variable. These findings indicate that older investors may shift their financial asset holdings towards Treasury bills in retirement to reduce consumption risk. It is worth noting that the positive relationship between real financial asset prices and the relative importance of middle-aged cohorts does not emerge as clearly using these measures of the demographic structure, which are coarser and divide up the age distribution more arbitrarily. Table A1 also shows that the results for stock prices relative to Treasury bill prices are similar to Figure 4, as are those for the relative price of bonds versus Treasury bills.
As noted above, both the dependent and the explanatory variables in Equation (3) are slow moving, raising the possibility of spurious correlations. To address this concern, Table 3 reports a series of panel unit root tests for the regressions underlying Figures 3 and 4, where these tests are performed on the residuals of the regressions.[4] Across the board, these tests strongly reject the null hypothesis of a unit root in the residuals, providing evidence against the possibility that unit roots are driving the results.
| Null: unit root (assumes common unit root process) |
Null: unit root (assumes individual unit root process) |
|||||
|---|---|---|---|---|---|---|
| Levin, Lin & Chu t-statistic | Breitung t-statistic |
ADF-Fischer Chi-square | PP-Fischer Chi-square | |||
| Real stock price | Statistic | −10.1 | −6.5 | 163.2 | 133.7 | |
| Probability | 0.0 | 0.0 | 0.0 | 0.0 | ||
| Real total return stock index | Statistic | −10.7 | −3.1 | 203.8 | 174.2 | |
| Probability | 0.0 | 0.0 | 0.0 | 0.0 | ||
| Real total return bond index | Statistic | −9.1 | −5.8 | 153.1 | 100.9 | |
| Probability | 0.0 | 0.0 | 0.0 | 0.0 | ||
| Real total return Treasury bill index | Statistic | −15.6 | −9.2 | 632.3 | 106.8 | |
| Probability | 0.0 | 0.0 | 0.0 | 0.0 | ||
| Stock price index relative to Treasury bill index | Statistic | −9.0 | −7.2 | 142.7 | 163.2 | |
| Probability | 0.0 | 0.0 | 0.0 | 0.0 | ||
| Total return stock index relative to Treasury bill index | Statistic | −10.2 | −6.6 | 169.6 | 178.0 | |
| Probability | 0.0 | 0.0 | 0.0 | 0.0 | ||
| Real total return bond index relative to Treasury bill index | Statistic | −5.9 | −2.3 | 97.9 | 106.2 | |
| Probability | 0.0 | 0.0 | 0.0 | 0.0 | ||
|
Source: author's calculations |
||||||
This section now explores the robustness of these results across countries. It does this by allowing γ1, γ2 and γ3 to be country-specific in Equation (3), by interacting the 16 country dummies with each of the demographic variables (Z1, Z2 and Z3). This specification thus estimates 48 demographic coefficients (3 coefficients for each of the 16 countries) and allows the restriction that γ1, γ2 and γ3 are the same across countries to be tested explicitly using likelihood ratio tests. If there is substantial heterogeneity across countries in the link between financial markets and demographics, the country-specific γ1, γ2 and γ3 parameters will add significantly to the explanatory power of the model and the likelihood ratio test will reject the null hypothesis that these coefficients are the same across countries. It is important to note that this more general specification is not the same as country-by-country regressions, as the time dummies in Equation (3) control for a common factor.
Table 4 reports the likelihood ratio tests across the estimations underlying Figures 3 and 4. The likelihood ratio test is calculated as LR = −2×(ln Lc − ln Lu), where LR is the likelihood ratio test statistic, Lc is the likelihood for the model that constrains γ1, γ2 and γ3 to be the same across countries, while Lu is the likelihood of the unconstrained model. This test statistic follows the chi-squared distribution with degrees of freedom equal to the difference in the number of parameters across the two specifications (45). Across specifications, the restriction that γ1, γ2 and γ3 are equal across countries is soundly rejected, as the test statistics are substantially above critical values at standard levels of significance. There is thus evidence of substantial heterogeneity across countries in the link between financial market outcomes and demographics.
| Constrained log-likelihood |
Unconstrained log-likelihood |
t-statistic | |
|---|---|---|---|
| Real stock price | −6,068 | −5,610 | 916 |
| Real total return stock index | −4,954 | −4,604 | 701 |
| Real total return bond index | −8,085 | −7,700 | 769 |
| Real total return Treasury bill index | −9,422 | −8,923 | 997 |
| Stock price index relative to Treasury bill index | −7,537 | −6,788 | 1,499 |
| Total return stock index relative to Treasury bill index | −6,011 | −5,314 | 1,395 |
| Real total return bond index relative to Treasury bill index | −5,384 | −4,287 | 2,193 |
|
Source: author's calculations |
|||
Figure 5 shows the country-specific age coefficients (α's) based on a third-order polynomial and real stock prices. The results for real total return stock indices, real total return bond indices and real total return Treasury bill indices are qualitatively similar and are thus omitted for brevity. As above, error bands of two standard deviations are plotted on either side of the α coefficients. Table 5 shows the corresponding panel unit root tests, which again strongly reject the null of a unit root in the residuals. The striking result in Figure 5 is that equity-based, English-speaking economies, such as Australia, Canada, New Zealand, the UK and the US appear to have age coefficients that do not conform well to the life-cycle hypothesis. In each of these cases, the α's describe a U-shape, suggesting that lower real stock prices are associated with having a large proportion of the population in middle age, while higher real stock prices are associated with larger shares of those in later stages of middle age and in retirement. While this age profile may be counter-intuitive, it conforms well to survey-based evidence on wealth accumulation, which implies that financial asset holdings peak late in life with little evidence of decumulation in retirement (see Figure 2, for example). In contrast, the age coefficients for countries such as Italy, Finland, Sweden, Norway and Japan exhibit the more familiar pattern from the pooled regression, which suggests that a higher share of older cohorts are associated with lower real stock prices. However, as many of these countries have bank-based financial systems where equity market participation among households is relatively limited, this result casts some doubt over whether the age profile is capturing some omitted factors (rather than demographic effects).
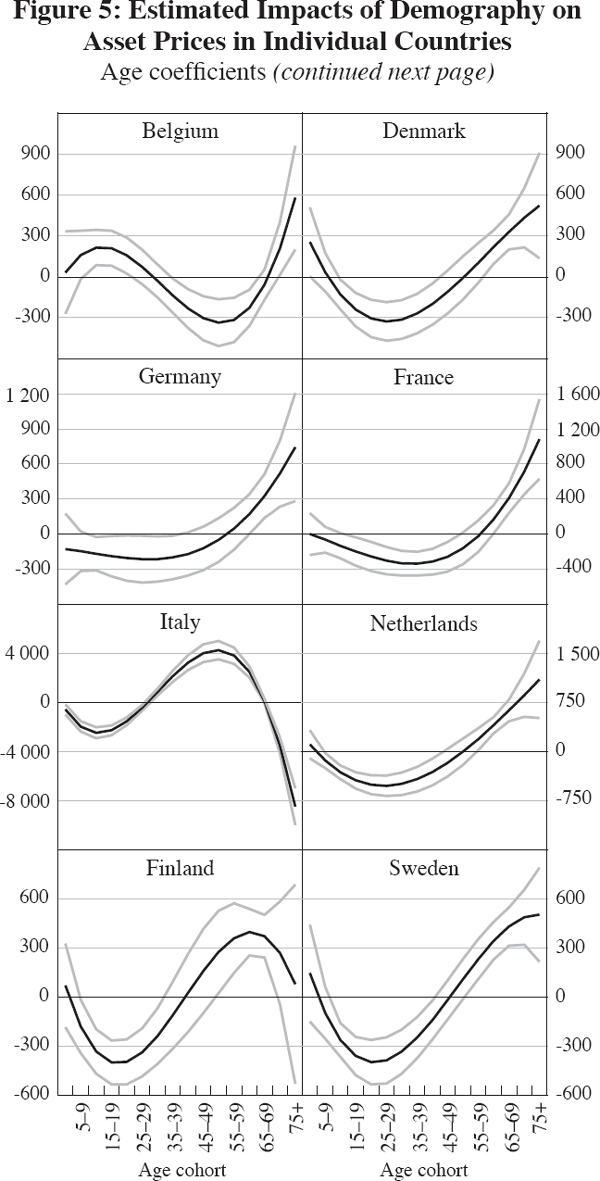
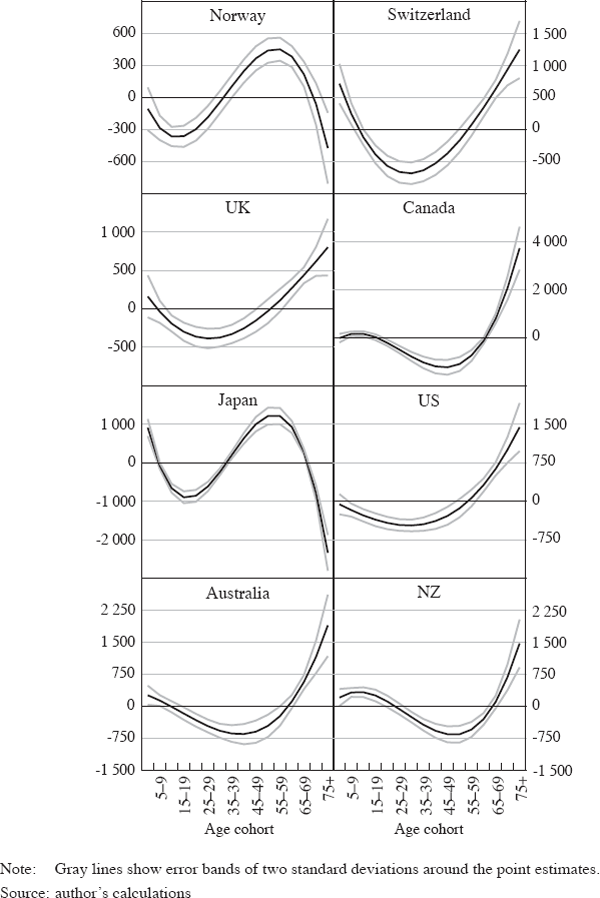
| Null: unit root (assumes common unit root process) |
Null: unit root (assumes individual unit root process) |
|||||
|---|---|---|---|---|---|---|
| Levin, Lin & Chu t-statistic | Breitung t-statistic |
ADF-Fischer Chi-square | PP-Fischer Chi-square | |||
| Real stock price | Statistic | −14.8 | −11.3 | 271.1 | 235.2 | |
| Probability | 0.0 | 0.0 | 0.0 | 0.0 | ||
| Real total return stock index | Statistic | −15.4 | −7.6 | 320.4 | 254.9 | |
| Probability | 0.0 | 0.0 | 0.0 | 0.0 | ||
| Real total return bond index | Statistic | −8.7 | −6.6 | 139.5 | 125.2 | |
| Probability | 0.0 | 0.0 | 0.0 | 0.0 | ||
| Real total return Treasury bill index | Statistic | −11.2 | −8.5 | 217.9 | 116.2 | |
| Probability | 0.0 | 0.0 | 0.0 | 0.0 | ||
| Stock price index relative to Treasury bill index | Statistic | −15.1 | −12.8 | 270.6 | 309.4 | |
| Probability | 0.0 | 0.0 | 0.0 | 0.0 | ||
| Total return stock index relative to Treasury bill index | Statistic | −14.7 | −10.5 | 269.4 | 284.7 | |
| Probability | 0.0 | 0.0 | 0.0 | 0.0 | ||
| Real total return bond index relative to Treasury bill index | Statistic | −12.0 | −10.2 | 208.0 | 234.3 | |
| Probability | 0.0 | 0.0 | 0.0 | 0.0 | ||
|
Source: author's calculations |
||||||
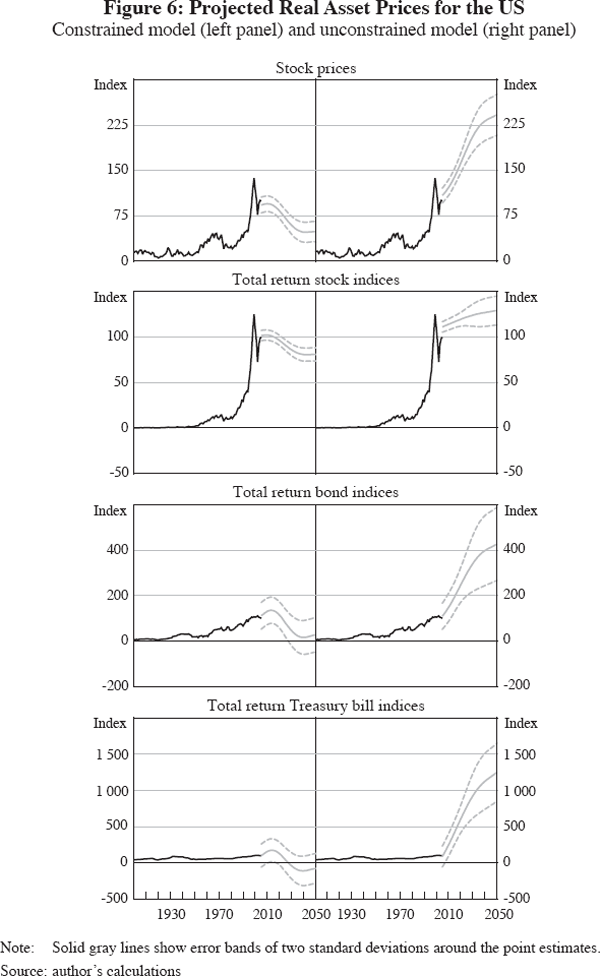
Figure 6 contrasts the constrained and the unconstrained models in terms of the implications of projected demographic change for real stock prices, the real total return stock index, the real total return bond index and the real total return Treasury bill index in the US. Population projections are based on the medium-variant United Nations projections, which provide annual data out to 2050. The figure is based on extrapolating Equation (3), with error bands of two standard deviations around the point estimates. Unlike the constrained model, which is not supported by the data, the unconstrained model predicts that real financial asset prices will rise as the population ages, due to the U-shaped pattern of the US age coefficients. While this is evidence against the asset-price meltdown hypothesis, and is consistent with survey evidence for the US that points to a build-up in financial wealth well into old age, it needs to be interpreted with caution for several reasons. First, survey evidence may be contaminated by cohort effects, which may distort the age profile. Second, these projections assume that the coefficients, which are based on data back to the early 1900s, are stable going into the future, which is highly unlikely. Third, these projections ignore the general equilibrium interactions that will occur as the population ages. Nonetheless, these projections underscore that, based on the historical association between real financial asset prices and demographics, it is hard to make a case for the asset-price meltdown scenario.
6.2 Asset returns and demographics
Having dealt with asset prices, this section now turns to the question of asset returns. Figure 7 shows the age coefficients (α's) for a third-order polynomial for real stock returns, real total returns on stocks, real total returns on bonds and real total returns on Treasury bills, along with error bands of two standard deviations on either side. Real returns are computed as nominal returns minus CPI inflation. Regressions are based on Equation (3) and, as above, are performed separately for each series of financial asset returns. Across financial assets, there is little evidence of a link between demographics and financial markets.
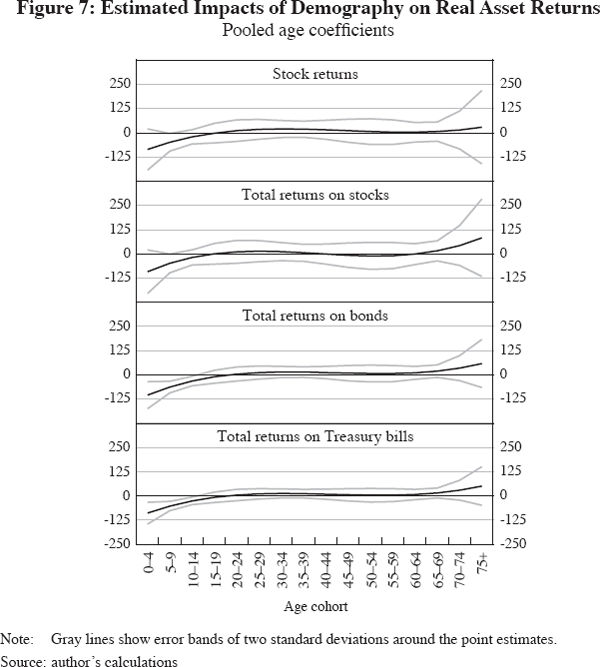
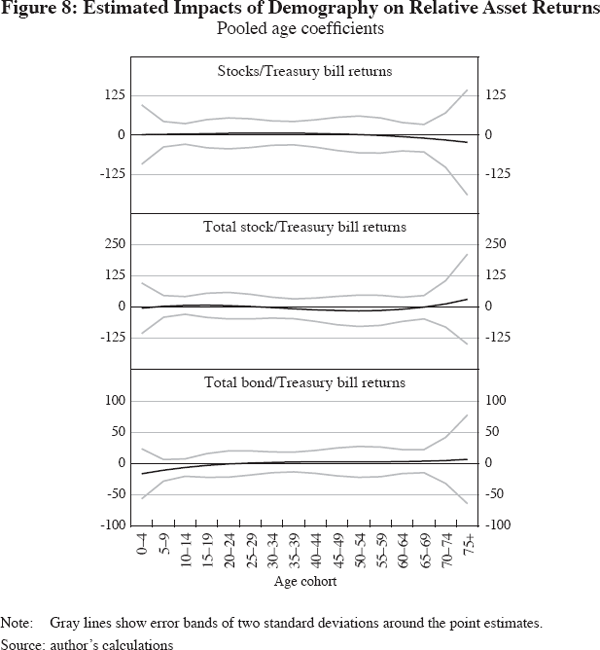
Consistent with earlier findings, including Poterba (2001), evidence of a link between demographics and returns is strongest for bonds and Treasury bills, where volatility is lower than for equity returns. However, it appears that only a high share of very young cohorts (aged between 0–4 and 10–14) are associated with significantly lower returns, while the association between returns and the rest of the age distribution is largely insignificant. In addition, there is little evidence that the equity premium and the premium on bonds over Treasury bills is significantly correlated with demographics, as can be seen from Figure 8, consistent with the generally weak evidence in favour of such a link in Ang and Maddaloni (2005).
These results contrast with Davis and Li (2003) who find that the relative importance of age groups 40–64 is positively and significantly correlated with changes in real stock prices, while it is negatively correlated with real bond yields. This finding could be due to the use of conventional demographic variables such as RAT40, which would suggest that the identified relationship is specific to that variable and not strong evidence in favour of a link between demographics and financial market returns.
The results in Table A2 show that real stock returns are indeed positively and significantly associated with RAT40, consistent with the result in Davis and Li (2003). However, this link weakens when total real returns on stocks are considered, with the RAT40 coefficient no longer significant at conventional levels. Meanwhile, total returns on bonds and Treasury bills have a positive significant association with the RAT40 variable. Across stocks, bonds and Treasury bills, the most robust result that stands out is that RAT0 is significantly and negatively correlated with real returns, a possible indication that higher youth dependency is correlated with financial market declines. This result is worth noting because it also emerges from the more general specification for which results are reported above, where young cohorts are associated with significantly lower returns. Table A2 also shows that there is little indication that the equity premium or the bond premium exhibit a significant empirical relationship with conventional demographic variables.
Because the real return series are close to white noise, problems associated with unit roots are likely to be less important than for asset prices. As a result, panel unit root tests are omitted for brevity, as are regression results by country.
7. Conclusions
Empirical evidence does not point to a strong historical link between demographics and financial markets. While the existing literature has found that the relative importance of middle-aged cohorts tends to be associated with relatively high real stock and bond prices, this paper shows that this relationship does not hold for countries with strong equity market participation among households, such as Australia, Canada, New Zealand, the UK and the US. In these countries, higher real financial asset prices tend to be associated with a large share of the population in the old tail of the age distribution, consistent with survey evidence from the US that shows that households build up financial wealth well into old age and then do little to run it down in retirement. Taken at face value, this suggests that real financial asset prices in these countries will actually rise as the population continues to age, though a number of considerations – including the changing nature of markets over time and general equilibrium considerations – caution against drawing this conclusion. Nonetheless, this finding underscores that historical evidence provides little support for the hypothesis that asset prices and returns will fall abruptly when the baby boomers retire.
Appendix A
| RAT0 | RAT15 | RAT40 | RAT65 | RAT4020 | RAT6520 | AA20 | |
|---|---|---|---|---|---|---|---|
| Real stock prices | |||||||
| Coefficient | 0.95 | −2.12 | 0.92 | −1.93 | 1.91 | −0.90 | 1.91 |
| t-statistic | 2.92 | −4.99 | 2.44 | −2.74 | 4.99 | −1.55 | 2.13 |
| R2 | 0.55 | 0.56 | 0.55 | 0.55 | 0.56 | 0.55 | 0.55 |
| Real total return stock indices | |||||||
| Coefficient | −0.50 | −0.38 | 1.25 | −1.00 | 1.38 | −0.90 | 0.92 |
| t-statistic | −3.53 | −2.05 | 7.79 | −3.26 | 8.41 | −3.57 | 2.34 |
| R2 | 0.83 | 0.83 | 0.84 | 0.83 | 0.84 | 0.83 | 0.83 |
| Real total return bond indices | |||||||
| Coefficient | 24.70 | −22.96 | −15.24 | −0.35 | −3.80 | 10.47 | 9.43 |
| t-statistic | 16.39 | −10.99 | −8.11 | −0.10 | −1.92 | 3.56 | 2.05 |
| R2 | 0.45 | 0.39 | 0.36 | 0.33 | 0.33 | 0.33 | 0.33 |
| Real total return Treasury bill indices | |||||||
| Coefficient | 64.89 | −63.08 | −39.72 | 5.52 | −9.37 | 33.33 | 32.44 |
| t-statistic | 15.81 | −11.18 | −7.80 | 0.56 | −1.75 | 4.20 | 2.61 |
| R2 | 0.45 | 0.40 | 0.37 | 0.34 | 0.34 | 0.35 | 0.35 |
| Relative stock prices/Treasury bill indices | |||||||
| Coefficient | −0.66 | −0.48 | 2.32 | −3.72 | 2.75 | −2.04 | 1.67 |
| t-statistic | −0.70 | −0.39 | 2.12 | −1.82 | 2.45 | −1.22 | 0.64 |
| R2 | 0.56 | 0.56 | 0.56 | 0.56 | 0.56 | 0.56 | 0.56 |
| Relative total return stock/Treasury bill indices | |||||||
| Coefficient | −0.11 | −0.70 | 1.13 | −1.52 | 1.50 | −0.80 | 1.30 |
| t-statistic | −0.37 | −1.76 | 3.22 | −2.30 | 4.17 | −1.49 | 1.55 |
| R2 | 0.65 | 0.65 | 0.65 | 0.65 | 0.65 | 0.65 | 0.65 |
| Relative total return bond/Treasury bill indices | |||||||
| Coefficient | −0.51 | −1.32 | 1.22 | 1.73 | 1.29 | 1.32 | 3.45 |
| t-statistic | −2.66 | −5.29 | 5.54 | 4.17 | 5.72 | 3.88 | 6.61 |
| R2 | 0.71 | 0.72 | 0.72 | 0.71 | 0.72 | 0.71 | 0.72 |
|
Source: author's calculations |
|||||||
| RATO | RAT15 | RAT40 | RAT65 | RAT4020 | RAT6520 | AA20 | |
|---|---|---|---|---|---|---|---|
| Real stock returns | |||||||
| Coefficient | −0.67 | 0.21 | 0.62 | 0.41 | 0.43 | 0.07 | 0.66 |
| t-statistic | −2.21 | 0.52 | 1.76 | 0.63 | 1.20 | 0.13 | 0.79 |
| R2 | 0.37 | 0.37 | 0.37 | 0.37 | 0.37 | 0.37 | 0.37 |
| Real total stock returns | |||||||
| Coefficient | −0.64 | 0.23 | 0.50 | 0.64 | 0.27 | 0.24 | 0.72 |
| t-statistic | −2.00 | 0.54 | 1.34 | 0.92 | 0.72 | 0.42 | 0.81 |
| R2 | 0.36 | 0.36 | 0.36 | 0.36 | 0.36 | 0.36 | 0.36 |
| Real total bond returns | |||||||
| Coefficient | −0.85 | 0.32 | 0.64 | 0.92 | 0.16 | 0.39 | 0.82 |
| t-statistic | −4.28 | 1.20 | 2.74 | 2.11 | 0.65 | 1.09 | 1.49 |
| R2 | 0.36 | 0.35 | 0.35 | 0.35 | 0.35 | 0.35 | 0.35 |
| Real total Treasury bill returns | |||||||
| Coefficient | −0.72 | 0.29 | 0.52 | 0.76 | 0.10 | 0.32 | 0.57 |
| t-statistic | −4.51 | 1.37 | 2.81 | 2.18 | 0.50 | 1.13 | 1.29 |
| R2 | 0.29 | 0.28 | 0.29 | 0.28 | 0.28 | 0.28 | 0.28 |
| Stock returns – Treasury bill returns | |||||||
| Coefficient | 0.05 | −0.08 | 0.10 | −0.35 | 0.34 | −0.25 | 0.09 |
| t-statistic | 0.19 | −0.24 | 0.31 | −0.60 | 1.05 | −0.53 | 0.12 |
| R2 | 0.41 | 0.41 | 0.41 | 0.41 | 0.41 | 0.41 | 0.41 |
| Total stock returns – Treasury bill returns | |||||||
| Coefficient | 0.08 | −0.06 | −0.03 | −0.12 | 0.18 | −0.08 | 0.15 |
| t-statistic | 0.28 | −0.17 | −0.08 | −0.19 | 0.52 | −0.17 | 0.18 |
| R2 | 0.39 | 0.39 | 0.39 | 0.39 | 0.39 | 0.39 | 0.39 |
| Total bond – Treasury bill returns | |||||||
| Coefficient | −0.13 | 0.03 | 0.11 | 0.15 | 0.06 | 0.07 | 0.25 |
| t-statistic | −1.15 | 0.17 | 0.85 | 0.63 | 0.43 | 0.32 | 0.80 |
| R2 | 0.41 | 0.41 | 0.41 | 0.41 | 0.41 | 0.41 | 0.41 |
|
Source: author's calculations |
|||||||
Footnotes
Asia and Pacific Department, International Monetary Fund, 70019th Street, N.W., Washington, D.C. 20431, USA. Tel: +1 (202) 623 6236. Fax: +1 (202) 589 6236. Email: rbrooks2@imf.org. I am grateful to Roberto Cardarelli, Hali Edison, James Gordon, Sam Ouliaris and Kenichi Ueda for many helpful discussions and comments. [1]
Recent articles on this subject have appeared in the Wall Street Journal (May 5, 2005), The Economist (May 19, 2006), Business Week (June 5, 2006), Fortune (June 26, 2006) and The Associated Press (July 5, 2006). [2]
Standard errors are White heteroskedasticity consistent. Likelihood ratio tests show that a third-order polynomial for the age coefficients best fits the data. Alternative specifications that were explored included second- and fourth-order polynomials. [3]
The tests are similar in spirit to the augmented Dickey-Fuller test, which is derived from a regression of the differenced residual on the residual without a constant and several lags of the dependent variable. For a survey of panel unit root tests, see Baltagi (2005). [4]
References
Abel AB (2001), ‘Will Bequests Attenuate the Predicted Meltdown in Stock Prices When Baby Boomers Retire?’, Review of Economics and Statistics, 83(4), pp 589–595.
Abel AB (2003), ‘The Effects of a Baby Boom on Stock Prices and Capital Accumulation in the Presence of Social Security’, Econometrica, 71, pp 551–578.
Ang A and A Maddaloni (2005), ‘Do Demographic Changes Affect Risk Premiums? Evidence from International Data’, Journal of Business, 78(1), pp 341–380.
Attanasio OP and GL Violante (2000), ‘The Demographic Transition in Closed and Open Economies: A Tale of Two Regions’, Inter-American Development Bank Research Department Working Paper No 412.
Bakshi GS and Z Chen (1994), ‘Baby Boom, Population Aging, and Capital Markets’, Journal of Business, 67(2), pp 165–202.
Baltagi BH (2005), Econometric Analysis of Panel Data, 3rd edn, John Wiley & Sons, NewYork.
Bergantino S (1998), ‘Lifecycle Investment Behavior, Demographics, and Asset Prices’, Doctoral dissertation, MIT Department of Economics.
Bohn H (2001), ‘Social Security and Demographic Uncertainty: The Risk-Sharing Properties of Alternative Policies’, in JY Campbell and M Feldstein (eds), Risk Aspects of Investment-Based Social Security Reform, Chicago University Press, Chicago, pp 203–241.
Börsch-Supan A, A Ludwig and J Winter (2005), ‘Aging, Pension Reform, and Capital Flows: A Multi-Country Simulation Model’, NBER Working Paper No 11850.
Brooks R (1998), ‘Asset Markets and Savings Effects of Demographic Transitions’, Doctoral Dissertation, Yale University Department of Economics.
Brooks R (2002), ‘Asset-Market Effects of the Baby Boom and Social-Security Reform’, American Economic Review, Papers and Proceedings, 92(2), pp 402–406.
Brooks R (2003), ‘Population Aging and Global Capital Flows in a Parallel Universe’, IMF Staff Papers, 50(2), pp 200–221.
Davis EP and C Li (2003), ‘Demographics and Financial Asset Prices in the Major Industrial Economies’, Brunel University Public Discussion Paper No 03-07.
Geanakoplos J, M Magill and M Quinzii (2004), ‘Demography and the Long-Run Predictability of the Stock Market’, Brookings Papers on Economic Activity, 1, pp 241–325.
Modigliani F and R Brumberg (1954), ‘Utility Analysis and the Consumption Function: An Interpretation of Cross-Section Data’, in KK Kurihara (ed), Post-Keynesian Economics, Rutgers University Press, New Brunswick, pp 388–436.
Poterba JM (2001), ‘Demographic Structure and Asset Returns’, Review of Economics and Statistics, 83(4), pp 565–584.
Poterba JM (2004a), ‘The Impact of Population Aging on Financial Markets’, NBER Working Paper No 10851.
Poterba JM (2004b), ‘Impact of Population Aging on Financial Markets in Developed Countries’, Federal Reserve Bank of Kansas City Economic Review, 89(4), pp 43–53.
Storesletten K, CI Telmer and A Yaron (2004), ‘Consumption and Risk Sharing over the Life Cycle’, Journal of Monetary Economics, 51(3), pp 609–633.
UN Population Division (2005), World Population Prospects: The 2004 Revision, United Nations, New York. Available at <http://esa.un.org/unpp/>.
Yoo PS (1994a), ‘Age Dependent Portfolio Selection’, Federal Reserve Bank of St. Louis Working Paper No 94-003A.
Yoo PS (1994b), ‘Age Distributions and Returns of Financial Assets’, Federal Reserve Bank of St. Louis Working Paper No 94-002B.