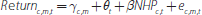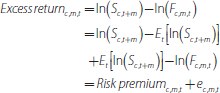Bulletin – March 2016 Global Economy The Term Structure of Commodity Risk Premiums and the Role of Hedging
- Download the article 369KB
Abstract
A standard theory used to explain commodity futures prices decomposes the futures price into the expected spot price at maturity of the futures contract and a risk premium. This article investigates the term structure of commodity risk premiums. We find that risk premiums vary across futures contract maturities, and that the term structure of commodity risk premiums differs between commodities. Furthermore, the risk premiums on crude oil and heating oil have fallen since the mid 2000s, consistent with increased financial investment in these futures markets. This article also outlines evidence to suggest that the existence of a commodity risk premium is related to the hedging activities of market participants.
Introduction
A common theory used to explain commodity futures prices states that the futures price equals the sum of the expected spot price at maturity of the futures contract and a risk premium.[1] Explanations for the existence of a risk premium typically view futures markets as a risk-transfer mechanism between market participants and therefore focus on the role of hedging. For example, commodity producers may want to enter into a short position, which is an agreement to sell a commodity at a specific date in the future at a price agreed when entering the contract. This provides a form of insurance against a decline in the spot price. Commodity consumers may want to enter into a long position to insure against increases in the spot price, and thereby agree to purchase a commodity at a future date. If the hedging activity of producers for a particular commodity is greater than that of consumers, there will be an excess of commercial market participants looking to enter a short position (a ‘net short hedging position’). In this case, the net hedging pressure theory implies that the futures price will be set below the expected future spot price to induce speculators – who do not have a commercial exposure they need to hedge – to balance the market by taking the opposing long position (Cootner 1960). In contrast, if the hedging activity of consumers for a particular commodity outweighs that of producers, there would be a net long hedging position. In this instance, the futures price would be set above the expected future spot price, so speculators would be compensated (through a positive expected return) for taking a short position in the commodity.
Therefore, ‘commodity risk premiums’ can be defined as returns that speculators expect to receive as compensation for taking another party's natural exposure to fluctuations in commodity prices through buying or selling a commodity futures contract. For example, suppose the spot price of oil is $50 per barrel today, and the market expects the spot price to be $60 in one year's time. If the futures price is equal to $57, then the risk premium speculators expect to receive for balancing the market and assuming the future spot price risk is $3. The rise of commodity index investing (where investors seek exposure to commodity prices via instruments linked to broad-based commodity indices) since the mid 2000s reflects investors' attempts to earn these risk premiums, as well as speculate on price movements and diversify across various asset classes.
Previous research on the effects of increased commodity futures trading by financial investors has typically focused on the impact on commodity price levels and volatility (see, for example, Dwyer, Gardner and Williams (2011)). Fewer papers have researched how financial investment may affect commodity risk premiums. If, for example, increased financial investment in commodities has ‘competed away’ the risk premium, then the futures price would, on average, more accurately reflect the expected future spot price. However, even if this were the case, this does not necessarily imply that increased financial investment in commodities has had a distortionary effect on commodity spot prices. Instead, it would suggest there has been a change in the relationship between commodity futures prices and the expected future spot price.
Moreover, studies investigating both the existence and determinants of commodity risk premiums have typically focused on risk premiums accruing to positions in relatively short-term commodity futures contracts. Few papers have examined risk premiums accruing to positions in longer-term futures contracts, and/or compared risk premiums for futures contracts on the same commodity but with different maturities (the term structure of commodity risk premiums). It is unlikely that risk premiums would be constant along a futures curve. For example, if speculators require a term premium to compensate for price uncertainty over a longer time period, the commodity risk premium may be larger (in absolute terms) for longer-maturity futures contracts. Moreover, the additional information afforded by examining risk premiums on longer-maturity futures contracts may lead to more accurate inferences regarding the determinants of commodity risk premiums.
In considering these issues, this article examines the term structure of commodity risk premiums for a broad sample of commodities, and considers how the term structure has changed over time alongside increased financial investment in commodities since the mid 2000s. It also discusses the net hedging pressure theory as a possible determinant of commodity risk premiums, before moving on to an econometric examination of the relationship between a measure of net hedging pressure and commodity risk premiums for three commodity subsectors: energy, agriculture, and metals. In particular, this article examines whether considering the term structure of commodity risk premiums can provide additional information about the role of net hedging pressure as a determinant of commodity risk premiums.
Commodity Risk Premiums for Individual Commodities
As discussed above, commodity risk premiums can be defined as the difference between the expected spot price at some specific future date and the futures price of a contract maturing at that same date. Ideally, commodity risk premiums would be measured ex ante using information on market participants' expectations for the spot price of a particular commodity at a specific future date. However, a time series of price expectations across a series of forecast horizons and for a broad range of commodities is not readily available. A commonly used alternative is to measure risk premiums ex post by calculating the average annualised futures' excess return, where the excess return is the return from buying a futures contract and settling that contract at expiration. This ex post calculation should equal the average ex ante commodity risk premium over a long sample under the assumption of unbiased expectations (see Appendix A for more details).
The empirical identification of non-zero commodity risk premiums for individual commodities has been somewhat inconclusive. This is potentially due to relatively high commodity price volatility relative to average returns, which leads to statistical problems with identifying risk premiums. A lack of reliable long-run data is another potential issue (Rouwenhorst and Tang 2012). However, a number of studies have found evidence of a positive risk premium when analysing returns of commodity indices, as the volatility of individual commodity returns is diversified away when included in an index. For example, Gorton and Rouwenhorst (2006) find evidence of a commodity futures risk premium that is similar in size to the historical risk premium of equities.[2] Notably, empirical identification of commodity risk premiums on individual commodities and commodity indices has typically focused on premiums accruing to positions in relatively short-term futures contracts.
To investigate commodity risk premiums for individual commodities we analyse a sample of 26 commodities over a range of futures contract maturities from 1986 to 2014 (where available).[3] Consistent with most previous studies, we also find that non-zero individual commodity risk premiums on short-dated contracts (e.g. one- to three-month maturities) are hard to identify statistically (Table 1).
| 1-month | 3-month | 6-month | 9-month | 12-month | |
|---|---|---|---|---|---|
| Agriculture | |||||
| Coffee | 13.4 | −4.3 | −6.6 | −5.7 | −7.2* |
| Corn | −5.4 | −4.2 | −5.8 | −4.5 | −3.5 |
| Cotton | −6.4 | −2.4 | −3.9 | −1.6 | −1.1 |
| Lean hogs | 3.8 | −0.5 | 3.4 | 3.6 | 3.7 |
| Live cattle | 13.0*** | 7.2*** | 5.5*** | 4.6*** | 3.7*** |
| Lumber | −11.0 | −7.5 | −7.2* | −4.7 | 1.4 |
| Milk | 4.0 | 4.3 | 2.3 | 2.8 | 3.7 |
| Orange juice | 9.6 | 1.5 | −2.0 | −2.9 | −3.7 |
| Soybeans | 11.0* | 6.2 | 4.2 | 4.8* | 4.0* |
| Soybean meal | 13.1** | 11.2*** | 9.4*** | 8.7*** | 7.7*** |
| Wheat (CBOT) | 6.5 | −2.6 | −3.9 | −2.7 | −2.5 |
| Wheat (MGEX) | 8.8 | 6.0 | 2.5 | 2.3 | 2.5 |
| Energy | |||||
| Crude oil | 5.7 | 6.7 | 7.4 | 8.0* | 8.4** |
| Heating oil | 9.0 | 6.8 | 7.0 | 7.5* | 7.5* |
| Natural gas | −16.3 | −14.6 | −9.3 | −6.8 | −3.9 |
| Metals | |||||
| Copper | 6.7 | 5.9 | 5.3 | 6.2 | 6.9* |
| Palladium | 2.8 | 6.5 | 9.2* | 9.3** | 5.0 |
| Platinum | 15.5 | 6.5 | 5.1 | 2.7 | −0.3 |
|
(a) *, **, and *** indicate returns are significantly different from zero at the 10, 5 and 1 per cent level, respectively; sample period 1986–2014; standard errors are robust to serial correlation and heteroscedasticity; CBOT denotes the Chicago Board of Trade; MGEX denotes the Minneapolis Grain Exchange Sources: Authors' calculations; Pinnacle Data |
|||||
However, in a number of cases we can identify both economically and statistically significant risk premiums on longer-dated futures contracts (e.g. nine- to twelve-month maturities). Further, Graph 1 shows that for a given commodity, the risk premium is typically not constant across futures contracts with different maturities, and the shape of the ‘risk premium curve’ differs substantially across commodities.
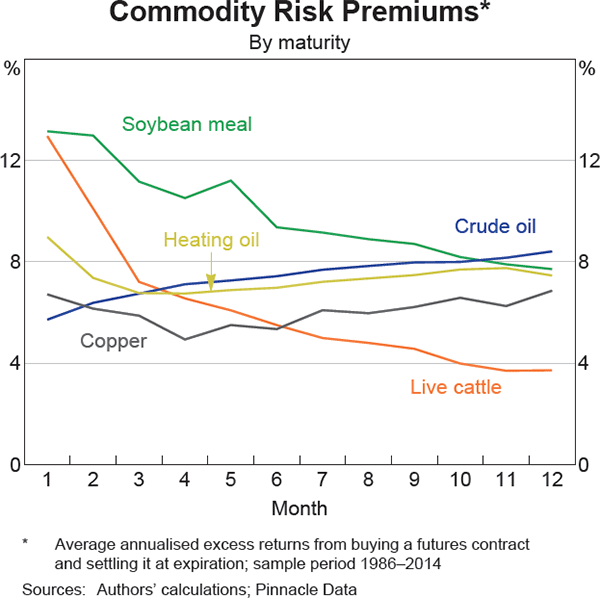
A positive commodity risk premium can be interpreted as the average return that a speculator would receive by entering a long position in a particular commodity futures contract and holding the contract to expiration. For instance, a strategy that consists of buying a crude oil futures contract with 12 months until expiration and then settling that contract at expiration would, on average over our sample, have received an 8.4 per cent annual return. Alternatively, under the net hedging pressure theory (discussed in more detail below), it can be viewed as the amount by which the futures price is discounted to the expected future spot price, which producers pay as a form of insurance to induce speculators to balance the market. Conversely a negative commodity risk premium occurs when consumers have to offer an incentive to induce speculators to enter a short position, and the absolute value of the risk premium represents the return the (short) speculator would receive. Therefore a larger absolute risk premium could reflect the fact there is greater net hedging demand for a particular commodity or at a particular maturity, and the slope of the ‘commodity risk premium curve’ could provide information about how net hedging demand differs at various maturities.
We also observe that the shape of ‘commodity risk premium curves’ have varied over time for some commodities. Consequently, we investigate below whether the change in market structure associated with the rise in financial investment in commodity futures has affected risk premiums.
The effect of financial investment on commodity risk premiums
The rise of commodity index investment since the mid 2000s, a key component in the financialisation of commodity markets, may have resulted in smaller absolute risk premiums as investors ‘compete away’ risk premiums.[4] A key aspect underlying the net hedging pressure theory is that some degree of commodity futures market segmentation from other financial markets acts to limit the number of investors in commodities markets, and prevents the risk premium from being competed away (Cheng and Xiong 2014). If this segmentation was reduced, more investors may enter the market to earn the risk premiums, which should cause the premiums to move towards zero. To the extent that the financialisation of commodities markets represents a decrease in market segmentation, this suggests that financialisation may be associated with smaller absolute risk premiums. Moreover, because much of the increased turnover in futures markets associated with index-fund investing has been through long positions in short-dated futures contracts, it might also be expected that risk premiums on short-maturity futures contracts have declined by more than longer-maturity contracts over time.
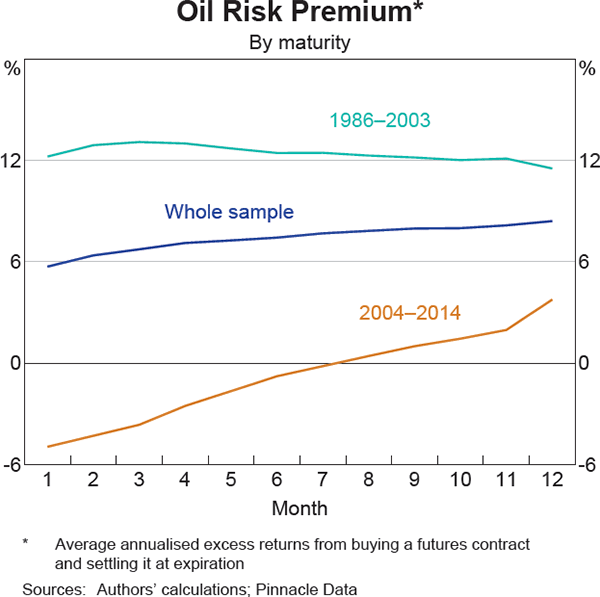
To investigate how financialisation may have affected the term structure of commodity risk premiums, our sample is split into two time periods – 1986–2003 and 2004–14 – to define ‘pre-financialisation’ and ‘financialisation’ periods.[5] Using 2004 as a break point is common in the literature and coincides with the beginning of a large increase in the volume of commodity futures trading. Also, to reflect how the degree of financialisation has differed between commodities, we further split our sample into ‘on-index’ commodities, which are included in both the Bloomberg Commodity Index (BCOM) and S&P GSCI, and ‘off-index’ commodities for those that are not included in either of these indices.[6]
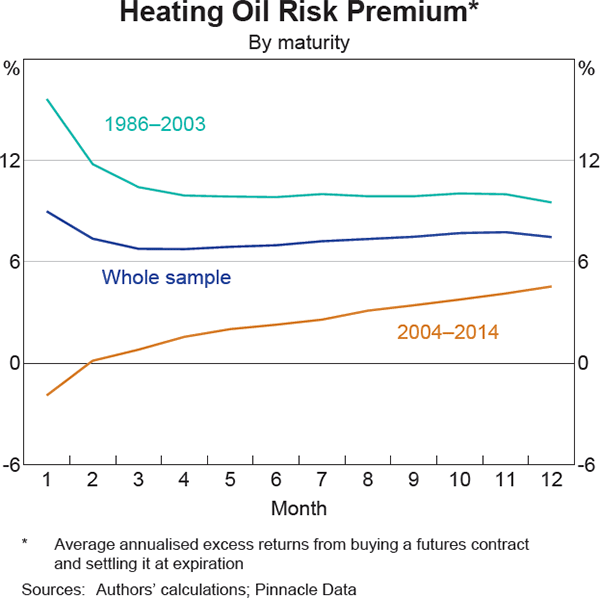
As expected, we find that for ‘off-index’ commodities splitting our sample into two time periods does not meaningfully change our results for identifying statistically significant non-zero commodity risk premiums across maturities from one to twelve months. However, for ‘on-index’ commodities, we identify two cases – crude oil and heating oil – where we find statistically significant positive risk premiums across most maturities over the ‘pre-financialisation’ period, but we cannot reject the possibility of a zero risk premium over the ‘financialisation’ time period. Moreover, we also find that the risk premium has declined by a greater magnitude on short-dated contracts (Graph 2 and Graph 3). Crude oil and heating oil are both highly financialised commodities. The results for these commodities are consistent with the rise of commodity index investment partially bidding down risk premiums, and also that this effect has generally been more pronounced at the short end of the futures curve.[7]
The Role of Net Hedging Pressure
The net hedging pressure theory suggests that the net of producers' and consumers' hedging activity – the ‘net hedging pressure’ (NHP) – will determine whether an inducement needs to be paid to entice speculators to balance the market by taking offsetting long or short positions in futures contracts (Cootner 1960). If the volume of producer hedging outweighs the volume of consumer hedging, there will be a net short hedging position and so speculators will need to be enticed to go long to balance the market. To achieve this, the price of the futures contract will be set below the expected future spot price, so that there is a positive expected return to taking a long position in the contract – a positive commodity risk premium. Conversely, if the volume of consumer hedging outweighs that of producers (a net long hedging position), this will yield a negative commodity risk premium. Thus the NHP theory predicts a negative relationship between NHP and commodity risk premiums.
A number of factors could influence producers' and consumers' demand for hedging at any given time, and therefore the extent of NHP and size of commodity risk premiums, for example:
- Inventories: the level of current and expected inventories would be expected to have a positive relationship with risk premiums. Holding all else constant, expectations of high inventory levels in the future (which provides more certainty around commodity access) should reduce the incentive for consumers to hedge, while producers may have a greater incentive to sell forward.
- Price volatility: higher current and/or expected price volatility may lead to greater demand from hedgers, and to speculators demanding greater compensation for bearing the risk associated with increased uncertainty about future spot prices. Thus, higher levels of current and expected price volatility may lead to greater absolute risk premiums.
Empirical support of a relationship between a measure of NHP and commodity risk premiums has been mixed, which could reflect a number of factors. One explanation is that the theory is oversimplified and that other factors, such as the risk-bearing capacity of broker-dealers (who act as intermediaries for hedgers in commodities markets) influences the relationship between NHP and commodity risk premiums (Etula 2010). Another potential explanation is that there may be issues with the data used to construct NHP variables (discussed further below). In particular, the Commodity Futures Trading Commission's (CFTC) commercial position data, which are used frequently in the literature, include the positions of swap dealers, who act as intermediaries in commodities markets. While swap dealers often act as intermediaries for producers and consumers, meaning that their positions reflect hedgers' positions, they can also act as intermediaries for speculators. Therefore, the NHP variable derived from the CFTC commercial positioning data may, to some extent, also reflect speculators' positioning.
A third explanation, which has not been explored in the literature to date, is that the relationship between NHP and commodity risk premiums could be more robust when examining premiums for longer-maturity contracts, if producers and/or consumers prefer to hedge over longer horizons.[8] For example, if producers of a given commodity have a strong preference for hedging their expected exposure to prices in 12 months' time, due to the nature of their production schedule, a larger short NHP may be associated with a larger positive risk premium on futures contracts with a 12-month maturity, but not necessarily for a futures contract with a one-month maturity. This also suggests that, for a given commodity, risk premiums could differ quite substantially for futures contracts of different maturities depending on producer and consumer hedging preferences.
Panel regression analysis
Some of the observations outlined above highlight the potential for hedging activity to explain variation in the term structure of commodity risk premiums. In light of this, the following analysis aims to investigate two questions which, to our knowledge, have not previously been investigated:
- Is there evidence of a statistically significant negative relationship between NHP and commodity risk premiums if premiums on longer-dated contracts are incorporated into the analysis?
- Is there stronger statistical evidence of a negative relationship between NHP and commodity risk premiums on longer-dated futures contracts than shorter-dated futures contracts?
We use panel regressions to examine the relationship between a measure of NHP and commodity risk premiums for commodity futures contracts with different maturities. The cross-section is made up of around 500 different contracts, with each representing a commodity contract with a particular maturity (e.g. oil with a one-month maturity, oil with a two-month maturity). Specifically, we estimate:
where Returncmt is the annualised excess return on commodity c, with contract maturity m, entered into at time t. The γcm are contract fixed effects that will account for omitted time-invariant factors, such as whether the commodity is storable. The θt are time fixed effects, which should help to capture omitted factors such as the global growth cycle.[9]
The main coefficient of interest is β, the coefficient on the independent variable NHPc,t. This variable is constructed using CFTC data on commercial positions in futures contracts. Specifically, it is measured as net commercial positions, scaled by gross commercial positions, or:
The NHP variable is commodity specific, but not contract specific. That is, while the NHP variable at time t differs between oil and copper, it does not differ between an oil futures contract with a one-month maturity and an oil futures contract with a two-month maturity. This is not ideal, as the NHP for a particular maturity is purported to be the actual determinant of the risk premium on that commodity futures contract. Using aggregated NHP data could mask differences in the NHP at different maturities as for some, if not all, commodities it is unlikely that the NHP is roughly equal across all maturities. For example, if producers and consumers have specific hedging preferences at different maturities or if there is seasonality in the positions data, this could make it harder to identify a statistically significant relationship between NHP and risk premiums. However, unfortunately data on commercial positions by maturity are not available.
Table 2 shows the results from the model.[10] If only risk premiums on the nearest-to-maturity contracts are included in the model, as is done in most of the literature, there is little evidence of a statistically significant relationship between NHP and risk premiums.[11] However, if returns on longer-dated futures contracts are included, we find strong evidence of a negative relationship, consistent with the NHP theory.
The results are similar if the β coefficient is allowed to differ for different commodity subsectors. If only the nearest-to-maturity futures contract is included, there is no evidence of a statistically significant relationship. However, when longer-dated futures contracts are included, there is evidence of a statistically significant negative relationship between NHP and risk premiums for the energy and agriculture subsectors, though not for the metals subsector.
The results show that including longer-dated futures contracts allows us to identify NHP as a determinant of commodity risk premiums. To some extent, this may reflect the increased number of observations, which should lead to more precisely estimated coefficients, rather than actually indicating a stronger relationship between NHP and risk premiums for longer-dated contracts. It should also not be surprising that we find a relationship between NHP and commodity risk premiums using all contracts rather than just short-term contracts given that the NHP variable is an aggregate of hedging positions across all maturities.
| Nearest-to-maturity contract | All contracts | |
|---|---|---|
| All sectors | −0.13 | −0.12*** |
| (0.08) | (0.04) | |
| By subsector | ||
| Energy | −0.58 | −0.60** |
| (0.47) | (0.30) | |
| Agriculture | −0.11 | −0.12** |
| (0.09) | (0.05) | |
| Metals | −0.12 | 0.03 |
| (0.18) | (0.12) | |
|
(a) *, ** and *** indicate significance at the 10, 5 and 1 per cent level, respectively; standard errors are shown in parentheses Sources: Authors' calculations; Pinnacle Data |
||
To estimate precisely whether there is a stronger relationship between NHP and commodity risk premiums at specific maturities, we would need the NHP variable to vary by maturity. As already noted, however, NHP data are not available by maturity. Instead we can try and infer something about the relationship across the curve by allowing β to differ across maturities. Overall, the results suggest that the relationship between NHP and risk premiums is negative (as theory suggests) and of a similar magnitude across different maturity buckets for commodities in the energy and agricultural subsectors, although the coefficients are only statistically significant on longer-dated futures contracts (Table 3).[12] In contrast, the relationship for the metals subsector between NHP and risk premiums is negative (and statistically significant) only at the short end of the futures curve.
| 1-month | 2-month | 3-month | 4–6 month | 7–12 month | 13–18 month | 19–24 month | |
|---|---|---|---|---|---|---|---|
| All sectors | −0.21** | −0.15 | −0.11 | −0.12** | −0.11*** | −0.14** | −0.02 |
| (0.11) | (0.10) | (0.08) | (0.06) | (0.04) | (0.05) | (0.09) | |
| By subsector | |||||||
| Energy | −0.72 | −0.45 | −0.50 | −0.62 | −0.60 | −0.68*** | −0.46*** |
| (0.46) | (0.44) | (0.44) | (0.43) | (0.36) | (0.23) | (0.10) | |
| Agriculture | −0.16 | −0.14 | −0.11 | −0.11* | −0.12** | −0.12** | 0.04 |
| (0.13) | (0.09) | (0.08) | (0.06) | (0.05) | (0.05) | (0.11) | |
| Metals | −0.26** | −0.09 | 0.00 | 0.03 | 0.12 | 0.02 | 0.06 |
| (0.11) | (0.08) | (0.09) | (0.12) | (0.14) | (0.12) | (0.14) | |
|
(a) *, ** and *** indicate significance at the 10, 5 and 1 per cent level, respectively; standard errors are shown in parentheses Sources: Authors' calculations; Pinnacle Data |
|||||||
Conclusion
This article has found evidence that suggests commodity risk premiums are not constant across futures contract maturities, and that the shape of the ‘commodity risk premium curve’ differs across commodities and over time. The data suggests that the risk premiums on crude oil and heating oil, especially on short-dated contracts, have declined over time consistent with increased financial investment in commodities putting downward pressure on risk premiums. One explanation for the existence of commodity risk premiums is the process of transferring price risk amongst market participants via hedging. Consistent with this, there is quite strong evidence of a relationship between a measure of net hedging pressure and commodity risk premiums, as suggested by the net hedging pressure theory, when we include returns on longer-dated futures contracts. Furthermore, the results suggest that there is evidence of a relationship between net hedging pressure and risk premiums for commodities in the energy and agriculture subsectors, but not in the metals subsector.
Appendix A
In this article commodity risk premiums were calculated by using the average annualised excess returns over a time period. The realised (continuously compounded) excess return for any contract will be the risk premium plus any unexpected deviation of the observed spot price at expiry from the expected future spot price (as at the date when the contract was entered):
where Fc,m,t is the futures price for commodity c, at time t, for maturity horizon m; Sc,t+m is the spot price for commodity c at the maturity date t + m; and Et indicates expectations at time t.
Assuming investors' expectations are unbiased, the average unexpected deviation
of the spot price – 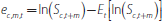 – over the sample should be zero. Therefore, on average, the excess return
should be equal to the risk premium. This method is consistent with the
methodology used in Gorton and Rouwenhorst (2006), which they note is consistent
with the definition of risk aversion in the finance literature.
– over the sample should be zero. Therefore, on average, the excess return
should be equal to the risk premium. This method is consistent with the
methodology used in Gorton and Rouwenhorst (2006), which they note is consistent
with the definition of risk aversion in the finance literature.
To calculate the excess returns, a database of futures contracts was constructed for 26 commodities.[13] These contracts were then used to construct a times series of the commodity futures curves. Specifically, a futures curve was constructed for each commodity, each month, with the date based on the expiry date of the futures contracts. The price of expiring contracts were considered to be the spot price, while the price of the contract maturing in one month's time was considered to be the one-month maturity price, and so on. These futures curves could then be used to look at the return of holding a futures contract (with a particular maturity) to maturity, the excess return, and therefore the ex post risk premium (the average of these returns).
It is important to note that futures curves with futures prices at each maturity were not available for most commodities, as most commodities do not have contracts expiring in each calendar month. For example, consider Table A1 below, which shows a commodity that has futures contracts expiring every second month. At time t, we would calculate returns for maturities 2, 4, 6, 8 etc. but then at time t + 1 we would have returns for maturities 1, 3, 5, 7 etc. As we move through time, we calculate returns for every month where an observation is available. We then take the arithmetic average of the returns across maturities. Further, the availability (and/or liquidity) of futures contracts over our sample and out to 24 months varied across commodities, and therefore futures curves could not be constructed for the same maturity profile across all commodities.
| Month | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Spot | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| t | Y | Y | Y | Y | Y | ||||
| t + 1 | Y | Y | Y | Y | |||||
| t + 2 | Y | Y | Y | Y | Y | ||||
| t + 3 | Y | Y | Y | Y | |||||
|
(a) Y denotes an observation; whole numbers denote months Source: RBA |
|||||||||
Footnotes
The authors are from International Department. [*]
An alternative notion, the theory of storage, argues the difference between the current spot and futures price can be explained by the cost that is incurred to store the commodity, the cost of capital which reflects the opportunity or financing cost associated with buying and holding the physical commodity and an implied convenience yield (Dwyer, Holloway and Wright 2012). [1]
Bhardwaj, Gorton and Rouwenhorst (2015) confirm that this finding holds using more recent data. [2]
For more details see Appendix A. [3]
For an overview of the literature of commodity financialisation, see Cheng and Xiong (2014). [4]
Some care must be taken in interpreting the results from sub-samples, as the assumption of unbiased expectations (see Appendix A) may be less valid over shorter periods, especially if the period does not contain a full commodity price cycle. [5]
The BCOM (formerly the Dow Jones-UBS Commodity Index) and S&P GSCI are commodity indices commonly used by commodity index traders. These indices are constructed by rolling over primarily short-dated futures contracts for a number of commodities and are used as a benchmark for a range of investment products (for example, exchange-traded funds and notes). [6]
Hamilton and Wu (2014) also find that the risk premium on short-term oil futures has decreased relative to longer-term futures since 2005, and attribute this to a sharp rise in oil futures trading volumes associated with the rise of commodity index investment. [7]
Another reason that the relationship may be more robust when longer-maturity futures contracts are considered is that these markets may have larger barriers to entry which limit the number of speculators in the market and therefore prevent the risk premiums from being competed away. [8]
The contract and time fixed effects should also help to capture any portion of the risk premium that is related to ‘systematic’ risk, which reflects correlation between commodity prices and other asset prices, rather than ‘idiosyncratic’ risk. Capital asset pricing models of commodity risk premiums, such as Hirshleifer (1988), suggest that systematic risk should also contribute to the risk premium. [9]
We estimate the model using cluster-robust standard errors as outlined in Thompson (2011). These errors are robust to serial correlation among errors for a single cross-sectional contract, cross-sectional correlation between contracts at time t and common serially correlated disturbances. A number of other less general error specifications were considered. However, given the nature of the data, and in particular the fact that the returns are estimated using overlapping horizons, we favoured a more general approach. [10]
We use the nearest-to-maturity contract, rather than the one-month-to-maturity contract, to be more consistent with the literature. [11]
Maturity buckets were used, rather than individual maturities, for two reasons. First, it significantly reduced the number of coefficients to be estimated. Second, for a sizeable proportion of the commodities there were relatively few observations for longer maturities, which could make it difficult to estimate separate coefficients for each maturity. Pooling the maturities is likely to ameliorate this issue somewhat. [12]
Please contact authors for further details on the commodities used. [13]
References
Bhardwaj G, G Gorton and G Rouwenhorst (2015), ‘Facts and Fantasies About Commodity Futures Ten Years Later’, Yale International Center for Finance 15–18.
Cheng I-H and W Xiong (2014), ‘Financialization of Commodity Markets’, Annual Review of Financial Economics, 6, pp 419–441.
Cootner PH (1960), ‘Returns to Speculators: Telser versus Keynes’, The Journal of Political Economy, 68(4), pp 396–404.
Dwyer A, G Gardner and T Williams (2011), ‘Global Commodity Markets – Price Volatility and Financialisation’, RBA Bulletin, June, pp 49–57.
Dwyer A, J Holloway and M Wright (2012), ‘Commodity Market Financialisation: A Closer Look at the Evidence’, RBA Bulletin, March, pp 65–77.
Etula E (2010), ‘Broker-Dealer Risk Appetite and Commodity Returns’ Federal Reserve Bank of New York Staff Report No 406.
Gorton G and KG Rouwenhorst (2006), ‘Facts and Fantasies about Commodity Futures’, Financial Analysts Journal, 62(2), pp 47–68.
Hamilton JD and JC Wu (2014), ‘Risk Premia in Crude Oil Futures Prices’, Journal of International Money and Finance, 42, pp 9–37.
Hirshleifer D (1988), ‘Residual Risk, Trading Costs, and Commodity Futures Risk Premia’, Review of Financial Studies, 1(2), pp 173–193.
Rouwenhorst KG and K Tang (2012), ‘Commodity Investing’, Annual Review of Financial Economics, 4, pp 447– 467.
Thompson SB (2011), ‘Simple Formulas for Standard Errors that Cluster by Both Firm and Time’, Journal of Financial Economics, 99(1), pp 1–10.