Bulletin – March 2012 Commodity Market Financialisation: A Closer Look at the Evidence
- Download the article 496KB
Abstract
There is some debate about whether financial investors have caused excessive increases in the level and volatility of commodity prices. These investors are viewed by some as being less concerned with fundamentals than traditional market participants and hence impeding the price discovery process – that is, they are destabilising speculators or ‘noise traders’. This article discusses the relationship between the futures markets for commodities (where financial investors are most active), and the spot markets. It then argues that the evidence does not support the hypothesis that financialisation has been the main driver of commodity price developments in the 2000s.
Introduction
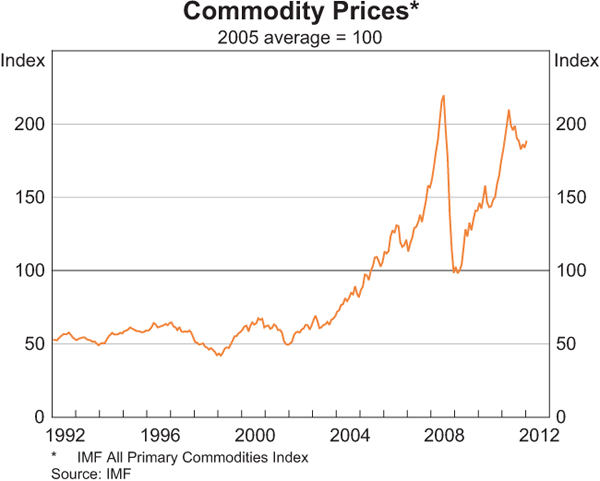
The past decade has seen a sharp increase in the level and volatility of commodity prices (Graph 1). This has occurred alongside a sharp increase in commodity demand from emerging market economies, but also in parallel with a rapid increase in both commodity derivatives trading and financial investor activity in commodity markets (Domanski and Heath 2007; Dwyer, Gardner and Williams 2011). That is, commodity markets have also become somewhat more like financial markets. This has given rise to considerable interest in the factors driving commodity prices – in particular the extent to which they have reflected ‘fundamental’ determinants of demand and supply versus the growing financialisation of commodity markets.[1]
If the decisions of financial speculators reflect informed views about fundamentals, financialisation can play a beneficial price discovery role. However, if financial speculators base their decisions on expectations of future price changes in the absence of ‘fundamental’ reasons to do so – such as ‘noise’ or ‘momentum’ trading behaviour – speculation could be destabilising (see, for example, Frankel and Rose (2009)).
Financial investors are generally most active in futures markets, rather than spot markets, as they do not want to take delivery of the physical commodity, which is expensive to store and to finance. Instead, the role of financial investors is to act on informed views on the prospects for supply and demand as well as to be paid to take on the commodity price risk that producers, and to a lesser degree consumers, wish to hedge. There are two broad channels through which commodity futures markets can affect the production and consumption decisions of participants in spot markets: (i) they allow firms to hedge their exposures to movements in spot prices, thereby smoothing their consumption expenditure and/or production cash flows over time and lowering the cost of capital; and (ii) they provide a potential source of influence over spot prices. If the sole function of futures markets was to provide hedging services to producers and consumers, the welfare implications would be unambiguously positive. But if speculation in futures markets causes futures prices to diverge from physical supply and demand fundamentals, this could have a distortionary effect on spot prices.
In considering this issue, we start by discussing the relationship between spot and futures prices from a theoretical perspective, before considering some of the empirical evidence. Overall, we conclude that there is no clear evidence that the financialisation of commodity markets has had a pervasive effect on commodity prices; instead, the evidence is consistent with fundamental supply and demand factors remaining the key determinants of commodity prices.
The Relationship between Futures and Spot Prices in Theory
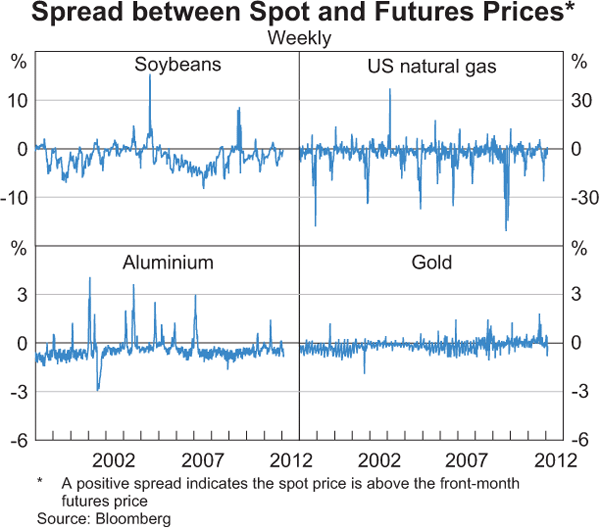
The ‘spot price’ is the cash price paid for the immediate delivery of a physical commodity, whereas the ‘futures price’ is the price of a standardised exchange-traded contract to purchase/sell a specific quantity of a commodity for delivery at a specified future date. In contrast to spot markets, investors in futures markets generally do not actually participate in the physical delivery of the commodity; instead they ‘roll over’ their contracts to the next futures contract if they wish to maintain their exposure. This is because physical delivery of the commodity gives rise to storage and financing costs, with little offsetting benefit to a financial investor from actually having a physical holding of, for example, soybeans or natural gas. Graph 2 shows the relationship between spot and (front-month) futures contract prices over time for soybeans, US natural gas, aluminium and gold, each of which have reasonably large and active futures markets.[2]
The theoretical relationship between futures prices and spot prices is based on a no-arbitrage condition.[3] This says that consumers and producers should remain indifferent between buying and selling the physical commodity at today's spot price, and entering into a futures contract that would allow them to buy and sell the commodity at a specified later date at today's futures price. In practice, financing constraints could limit this process to some extent. Assuming that the commodity is storable and that (well-informed) participants are able to freely access both the spot and futures markets (i.e. there are no financing or institutional constraints), then an unexpected increase in the futures price would, all else equal, allow agents to profit from buying the commodity today at the (relatively low) spot price, and selling it in the future at the (relatively high) futures price. This would then place upward pressure on the spot price and/or downward pressure on the futures price until the no-arbitrage condition was restored.
Importantly, however, the no-arbitrage condition does not imply that the futures price should equal the spot price, or that a given change in the futures price will be accommodated by a proportionate change in the spot price. This is because the arbitrage relationship also takes into account some underlying differences between physical commodities and futures contracts, which may themselves vary over time.
- First, there is an opportunity cost associated with buying and holding the physical commodity, as opposed to entering into a contract to purchase the commodity at a future date and earning interest on the funds set aside for this future purchase in the meantime. This opportunity cost, which is captured by the foregone interest rate, acts to reduce (increase) the return from buying (selling) the physical commodity at the spot price relative to entering into a futures contract.
- Second, holdings of physical commodities incur storage costs whereas futures contracts do not. Storage costs act to reduce (increase) the return from buying (selling) the physical commodity at the spot price relative to entering into a futures contract.
- Third, there is a ‘convenience yield’ from holding the physical commodity, which is the benefit of having assured access to the commodity in the event of a supply disruption. This acts to increase (reduce) the return from buying (selling) the physical commodity at the spot price relative to entering into a futures contract.
The no-arbitrage condition describing the relationship between futures and spot prices can be represented by the following equation:[4]
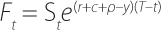
Where: Ftand Stare the futures and spot prices at time t; r is the risk-free annual interest rate; c is the cost of storing the physical commodity; y is the convenience yield earned from holding the physical commodity; and T is the maturity date for the futures contract.[5] This basic model captures the cost of freely available finance, but can be extended to account for financing constraints and/or risk aversion by incorporating a risk premium.[6] It can be seen from this equation that the futures price will only be close to the spot price if the net impact of the interest rate, storage costs and convenience yield (r+c−y) is very small, or the futures contract relates to a very near delivery date (so that (T−t) is very small).
Similarly, changes in futures and spot prices need not be proportionate, depending on how these other variables change. For example, if an increase in the futures price encourages a build-up of inventories, storage costs may also rise (as warehouse space becomes scarce) and the convenience yield may fall (as the benefits of physically holding a more abundant commodity diminish). The observed increase in the spot price in response to the higher futures price would then be smaller than otherwise.
The no-arbitrage condition also does not specify whether the spot or futures price adjusts in response to an unanticipated change in one of the variables in the equation. If, for example, there is an unexpected increase in the futures price, the no-arbitrage condition could be restored by: the futures price subsequently falling again; the spot price rising; or some combination of the two. In practice, this will depend on the extent to which the unexpected change in the futures price is perceived to reflect a genuine change in fundamentals, as well as the time horizons of participants in the spot and futures markets.
If an increase in the futures price is viewed as revealing genuinely new information about fundamentals, firms that supply the physical commodity to the spot market will have an incentive to build inventories, while firms that demand the physical commodity will have an incentive to stockpile purchases for future use. This should create excess demand for the commodity in the spot market at the current price, thereby pushing the spot price up until the no-arbitrage condition is restored. In this scenario, futures prices would only distort spot prices if there are information failures – that is, if participants in the spot market mistake speculative price developments for genuine price discovery .
However, if an increase in the futures price is not considered to reveal any genuinely new information about fundamentals, the response of firms in the spot market (and well-informed investors in the futures market) will depend on their views about how long the apparent ‘bubble-like’ conditions will be sustained, and how long they are willing to hold their positions.[7] Such a situation could arise, for example, due to the influence of so-called ‘noise’ or ‘momentum’ traders, who are either less well-informed than other market participants, or who actively choose to ignore fundamentals (Shleifer and Summers 1990; Reichsfeld and Roache 2011). If the deviation from fundamentals is considered temporary, firms that supply the physical commodity to the spot market will have an incentive to increase their short positions in the futures market (i.e. enter into agreements to sell the commodity at a future date at the relatively high futures price, rather than at the (lower) expected spot price). At the same time, firms that demand the commodity in the futures market will have an incentive to reduce their long positions in the futures market. This should place downward pressure on the futures price, to the point where the no-arbitrage condition is restored.
Alternatively, participants in the spot market may suspect that a rise in the futures price which is not justified by fundamentals could be sustained – for example, due to herding behaviour among ‘noise traders’. In this case, producing firms may be tempted to withhold supply to the spot market (in expectation that the higher futures prices will translate into higher spot prices) and reduce their short futures positions (which provide insurance against falls in the spot price). At the same time, consuming firms will have an incentive to stockpile the spot commodity for future use and increase their long futures positions (which provide insurance against increases in the spot price). Other, better-informed, financial speculators may also be encouraged to bet on future price increases in order to book short-term profits. This process could simultaneously drive spot and futures prices higher, and even further from the price implied by fundamentals. While it may be reasonable to expect fundamentals to eventually reassert themselves, so-called ‘rational bubbles’ could nevertheless act to distort spot and futures prices for some time.
The Relationship between Futures and Spot Prices in Practice
With that background in mind, it is useful to examine how these relationships play out in practice. To this end, we perform Granger causality tests to examine the empirical relationship between daily changes in spot and (front-month) futures prices – that is, whether changes in one price systematically precede changes in the other – for a range of individual commodities.[8] In the context of asking how financial speculators could influence prices, there are four possible outcomes of these tests, each with different implications:
- If changes in futures prices are found to Granger-cause changes in spot prices, this suggests that price discovery is occurring in the futures market. This could indicate that the futures market tends to absorb news about changes to fundamentals more quickly than the spot market. A less benign interpretation could be that speculative developments in futures prices are distorting spot prices (at least temporarily).
- If changes in spot prices are found to Granger-cause changes in futures prices, this suggests that price discovery is occurring in the spot market. In this case, any speculation-driven changes in futures prices are unlikely to distort spot prices.
- If we find evidence of bi-directional Granger causality (i.e. changes in futures prices Granger-cause changes in spot prices and changes in spot prices Granger-cause changes in futures prices) this indicates that spot and futures prices are jointly determined. This could indicate either that there are a large number of participants with access to both markets (such that perceived news is simultaneously reflected in both the futures and spot markets) or that there are institutional factors which enforce a close mechanical relationship between the two markets.
- Lastly, if no Granger-causal relationships are detected, this may suggest that spot and futures markets are sufficiently segmented to prevent arbitrage from occurring, and therefore that developments in one market are unlikely to affect the other. Alternatively, arbitrage may still hold, with the Granger-causal relationships existing only on an intraday basis or adjustment occurring primarily through changes in other variables (e.g. through storage costs or the convenience yield).
Granger causality tests are estimated for 10 commodities, covering four commodity classes – base metals, agriculture, energy, and precious metals – over a sample period from 1997 to 2011. Details of the price measures used are shown in Appendix A. We also perform the tests over two sub-periods – 1997 to 2002 and 2003 to 2011 – to determine if the relationships between spot and futures prices have changed as commodity futures markets have become much larger. The tests are conducted using a standard GARCH (1,1) model for lag lengths ranging from 1 to 10 days.[9] Table 1 presents the results of the Granger causality tests for lag lengths of 1, 5 and 10 days (which are generally representative of the results obtained using other lag lengths).
The results for base metals (aluminium, copper, nickel and zinc) are mixed, but there is little evidence of a consistent one-way Granger-causal relationship from futures prices to spot prices (i.e. that changes in futures prices systematically precede changes in spot prices). Instead, we find evidence of a bi-directional Granger-causal relationship for copper and nickel, but almost no evidence of a Granger-causal relationship in either direction for zinc or aluminium. The bi-directional Granger-causal relationships between futures and spot prices for copper and nickel suggest that these prices are typically jointly determined and are therefore likely to be anchored to a common set of fundamentals. On the other hand, while the absence of any Granger-causal relationship between changes in spot and futures prices for aluminium and zinc could suggest that there are barriers to arbitrage between the two markets, it is arguably more likely that futures and spot price adjustments are occurring on an intraday basis, which is not captured by the daily frequency of our data. It is also possible that some adjustment occurs through other factors, such as storage and/or financing costs.
| 1997–2011(b) | |||
|---|---|---|---|
| 1 day | 5 days | 10 days | |
| Aluminium | None | None | None |
| Copper | Both | Both | Both |
| Nickel | Both | Both | None |
| Zinc | None | None | None |
| Corn | Futures → Spot | Futures → Spot | Futures → Spot |
| Soybeans | Futures → Spot | Futures → Spot | Futures → Spot |
| Wheat | Futures → Spot | Futures → Spot | Futures → Spot |
| US natural gas | Futures → Spot | Futures → Spot | Futures → Spot |
| Gold | Spot → Futures | Spot → Futures | Spot → Futures |
| Silver | Both | Both | Spot → Futures(c) |
| 2003–2011 | |||
| 1 day | 5 days | 10 days | |
| Aluminium | None | None | None |
| Copper | Both | Both | Both |
| Nickel | Both | Both | Futures → Spot(d) |
| Zinc | None | None | None |
| Corn | Both | Futures → Spot(c) | None |
| Soybeans | Futures → Spot | Futures → Spot | Futures → Spot |
| Wheat | Futures → Spot | Futures → Spot | None |
| US natural gas | Futures → Spot | Futures → Spot | Futures → Spot |
| Gold | Spot → Futures | Spot → Futures | Both |
| Silver | Spot → Futures | Spot → Futures | Spot → Futures |
|
(a)Results are statistically significant at the 5 per cent level, except
where otherwise indicated; London Metal Exchange (LME) prices are used
for base metals, Chicago Board of Trade (CBOT) prices are used for agricultural
commodities Sources: Bloomberg; authors' calculations |
|||
The results for the agricultural commodities (corn, soybeans and wheat) are much more uniform, with strong evidence that daily changes in futures prices Granger-cause daily changes in spot prices. This is not surprising, as spot markets for agricultural commodities tend to be relatively fragmented (i.e. they consist of a relatively large number of producers with specialist local knowledge). These results also hold in the 2003–2011 sub-sample, except at longer lag lengths for corn and wheat where there no longer appears to be a Granger-causal relationship in either direction. These findings indicate that, for these agricultural commodities, developments in futures prices have a bearing on spot prices.
For US natural gas, we also find strong evidence that daily changes in futures prices Granger-cause daily changes in spot prices. Oil prices are deliberately excluded from the Granger causality analysis as there are certain institutional features of the oil market which complicate the relationship between spot and futures prices. In particular, there is arguably no independent benchmark spot market for oil (see Fattouh (2011) for a more detailed discussion of the features of the oil market). So, for example, for West Texas Intermediate (WTI) oil, the benchmark (Cushing crude oil) spot price trades at parity to the front-month futures price for all but a 3-day delivery scheduling period that commences when the current front-month futures contract expires.
For precious metals (gold and silver) we find some evidence that spot prices Granger-cause futures prices, particularly over the most recent period. Gold spot prices Granger-cause gold futures prices (although with some evidence of bi-directionality at longer lag lengths in the more recent period). For silver, there is a largely bi-directional Granger-causal relationship over the full sample period, but over the 2003–2011 period, spot prices are found to Granger-cause futures prices. There does, however, appear to be some weak evidence of a return to bi-directional Granger-causality during the rapid run-up in silver prices between mid 2010 and end 2011, suggesting that developments in silver futures prices did have an effect on spot prices during this so-called ‘bubble’ episode. More generally, the apparent influence of precious metals spot prices on futures prices is likely to be related to the relatively large and liquid nature of spot markets for these commodities, which in turn reflects their unique status as financial assets with relatively low storage costs. Related to this, the growth in physically backed commodity exchange-traded products for precious metals may also be a factor, as these products require investment in the underlying physical commodity at the spot price (Kosev and Williams 2011).
Pulling all this together then, it seems the relationship between spot and futures prices is a complex one, varying across commodities, sometimes within commodity classes, and also over time. There is evidence for agricultural commodities and US natural gas that changes in futures prices lead those in spot markets. If futures prices for these commodities reflect fundamentals, these markets can be viewed as being welfare enhancing, with the participation of financial speculators adding to the liquidity of these markets and improving price discovery. However, if there is evidence of speculation in these futures markets by ‘noise’ or ‘momentum’ traders, this has the potential to distort the corresponding spot prices, with adverse consequences for the real economy. Consequently, to distinguish between these competing views on the role of financial speculators, it is important to evaluate the evidence on the relationship between futures prices and macroeconomic fundamentals.
Are Futures Price Developments Consistent with Fundamentals?
Previous Reserve Bank work has found that, in general, the large increase in the number of financial investors in commodity markets over the past decade has not significantly altered price dynamics (see Dwyer et al (2011)). The main pieces of evidence in support of this view are that:
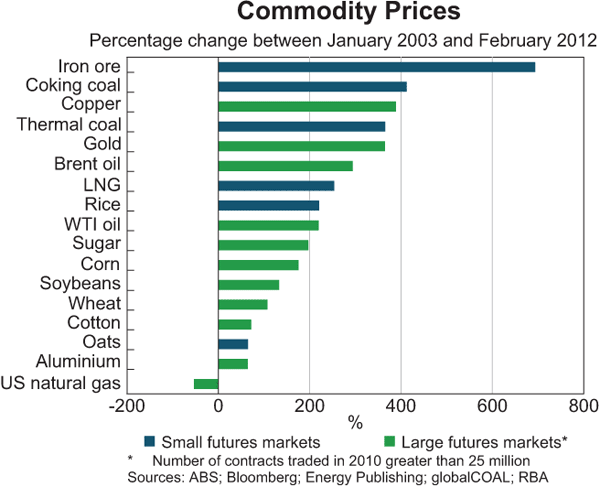
- price increases have been just as large (if not larger) for some key commodities that do not have well-developed financial markets as for those that do (Graph 3);
- there has been substantial variation in the price behaviour of individual commodities, even among those that have large, active derivatives markets (such as natural gas and oil);
- the recent increase in the correlation between commodity prices and other financial prices, such as equities – which is commonly cited as evidence that financial speculators are affecting prices – is in fact not that unusual by longer-run historical standards, with previous episodes of increased correlation occurring prior to the recent influx of financial investors into commodity markets (Graph 4); and
- there does not appear to have been the large increase in commodity inventories that we would expect to accompany speculation-driven price rises (as discussed in the earlier section on the theoretical relationship between futures and spot prices).
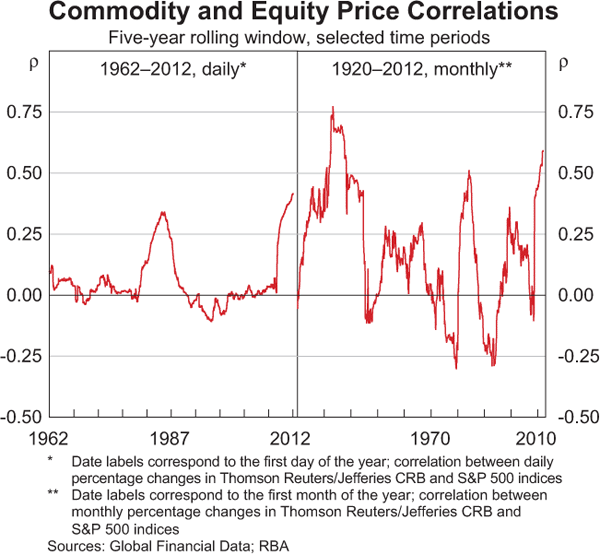
In this article, we present two further pieces of analysis which suggest that, in general, developments in futures prices have been consistent with fundamentals. First, we show that the relationship between commodity prices and the global output gap over the past decade is broadly in line with that seen over a longer time horizon (although the omission of supply-side factors makes it difficult to draw any firm conclusions about the relationship between commodity prices and fundamentals based on the output gap alone). Second, we use principal component analysis to show that since 2003, individual commodity prices have been driven primarily by a single common factor, which appears to be related to macroeconomic fundamentals.
Commodity prices and the global output gap
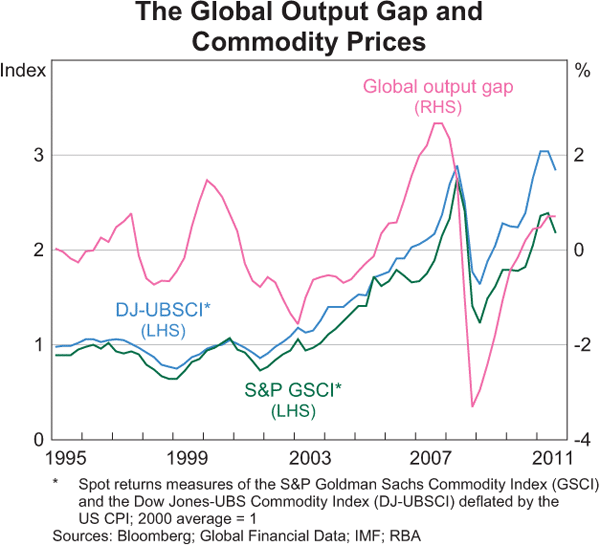
It has been argued that the global output gap is an important determinant of the cyclical behaviour of commodity prices, since commodities are used as an input to production (and typically it takes some time for commodity supply to respond to changes in demand). As shown in Inamura et al (2011), there appears to be some evidence of this, with a broad co-movement over time between the global output gap (measured as the difference between actual and potential global GDP)[10] and various commodity price indices (reproduced in Graph 5).[11]
Proponents of this view suggest that increased financial investment in commodity markets over the past decade has resulted in an upward shift in the relationship between commodity prices and the global output gap. Abstracting from supply factors, the intuition here is that financialisation constitutes a source of increased demand for commodities which is unrelated to macroeconomic ‘fundamentals’ (as captured by the output gap). Graph 6 plots the relationship between real commodity prices and the global output gap from 1971. There does indeed appear to have been an upward shift in the relationship between real commodity prices and the global output gap between 1995–2002 and 2003–2011, consistent with the financialisation hypothesis. However, taking a longer-run historical perspective, it is evident that the relationship observed over the 2003–2011 period is around average, whereas it is the relationship from 1995–2002 (and also 1987–1994) that looks unusual. That is, it is the period of low and falling real commodity prices during the latter part of the 1980s and the 1990s that looks more unusual, rather than the most recent period.
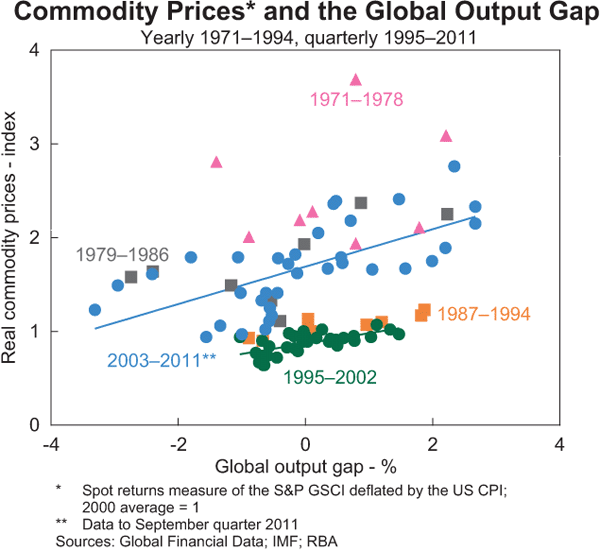
As noted above, however, this analysis omits supply-side factors, which are also important determinants of commodity prices. In particular, supply conditions were tight in the 1970s – associated with the oil price shocks – but eased in the 1980s in response to the earlier increase in prices.
So, from a longer-run perspective, the relationship between commodity prices and the global output gap in recent years does not look unusual. In any event, the omission of supply-side factors means that any change in this relationship cannot, of itself, be attributed to the financialisation of commodity markets in recent years.
Principal component analysis
An alternative way to examine the extent to which developments in commodity futures prices have been consistent with macroeconomic fundamentals is through principal component analysis. This statistical technique identifies whether there are common factors driving movements in an underlying set of observed variables, and how important they are, without having to specify what those factors might be. Drawing on this analysis, together with broader evidence on the drivers of commodity prices (see, for example, Connolly and Orsmond (2011); Dwyer et al (2011)), we can infer the extent to which these common factors are related to macroeconomic fundamentals.
This analysis was conducted on quarterly price changes for a broader set of 20 commodities over two sample periods: the September quarter 1990 to the December quarter 2002 and the March quarter 2003 to the December quarter 2011.[12] By comparing the results from these two periods, we can gain some insights into the effect of financial investment in commodity markets.
The results suggest that, since 2003, one common factor (i.e. the first principal component) has explained 40 per cent of the total variation in our set of 20 commodity prices in change terms (Table 2), with the next most important factor accounting for only 12 per cent.[13] In levels terms, the first principal component explains almost 70 per cent of the variation since 2003. A number of statistical tests indicate that there is only one significant common factor.[14] The results show that the first principal component has become more important over the past decade compared with the 1990s, when it only explained 23 per cent of the variation in commodity prices in change terms (and just under 40 per cent in levels terms). Moreover, across the various commodities, the first factor loadings (i.e. the correlations between changes in the commodity's price and the first principal component) are reasonably uniform within the recent sub-period (Table 3). US natural gas prices are one notable exception, consistent with the large (idiosyncratic) increase in supply associated with the shale gas ‘revolution’ together with the fact that US natural gas is restricted to the domestic market due to a lack of international transportation infrastructure. Agricultural prices also tend to have somewhat lower loadings on the common factor. This seems likely to reflect the importance of idiosyncratic – particularly weather-related – supply factors in driving futures prices for agricultural commodities.
| Share of variation explained (per cent) | ||
|---|---|---|
| Principal component | 2003:Q1–2011:Q4 | 1990:Q3–2002:Q4 |
| 1 | 40 | 23 |
| 2 | 12 | 14 |
| 3 | 9 | 11 |
| 4 | 7 | 8 |
| 5 | 6 | 7 |
| 6 | 5 | 7 |
| 7 | 4 | 6 |
| 8 | 3 | 5 |
| 9 | 3 | 4 |
| 10 | 3 | 3 |
| … | ||
| 20 | 0 | 0 |
|
Source: authors' calculations |
||
The dominance of the first principal component shows that there has been one major common driver of developments in commodity prices, particularly in the post-2003 period. This appears likely to be related to known macroeconomic developments over this period – in particular, the combination of an unexpectedly large increase in demand for commodities and sluggish supply growth. For example, the pair-wise correlation between the first principal component and quarterly growth in global industrial production is 0.7 over the recent period. While this does not control for other relevant variables, such as supply factors, it is nevertheless broadly consistent with the results obtained from a more fully specified model in Arbatli and Vasishtha (2012). The alternative hypothesis, which is that financialisation has been by far the most important influence on commodity prices, is a much less plausible explanation, in large part because there is no reason to suspect that this has an element to it that is common across a rather disparate set of commodities, a number of which are not even included in the major commodity indices used by financial investors.
| Correlation between price change and first principal component | ||
|---|---|---|
| 2003:Q1–2011:Q4 | 1990:Q3–2002:Q4 | |
| Aluminium | 0.82 | 0.61 |
| Copper | 0.79 | 0.56 |
| Oats | 0.77 | −0.48 |
| Silver | 0.76 | −0.12 |
| Brent oil | 0.75 | 0.89 |
| WTI oil | 0.72 | 0.87 |
| Heating oil | 0.71 | 0.82 |
| Corn | 0.66 | −0.48 |
| Cotton | 0.64 | 0.11 |
| Zinc | 0.63 | 0.31 |
| Soybeans | 0.62 | −0.21 |
| Lead | 0.61 | 0.24 |
| Coffee | 0.55 | 0.12 |
| Nickel | 0.54 | 0.48 |
| Cocoa | 0.51 | −0.23 |
| Gold | 0.51 | 0.15 |
| Wheat | 0.50 | −0.43 |
| Rice | 0.46 | −0.32 |
| Sugar | 0.39 | 0.09 |
| US natural gas | 0.38 | 0.33 |
|
Source: authors' calculations |
||
Conclusion
Overall, while financial speculation at times may have exerted some influence on some commodity prices beyond fundamentals, the available evidence does not support the hypothesis that financialisation has been the main driver of commodity price developments in the 2000s. More generally, the theoretical relationship between commodity futures and spot prices does not imply that changes in futures prices need necessarily lead to changes in spot prices. In practice, this is supported by the results of Granger causality tests, which point to substantial variation across individual commodities.
Appendix A
| Commodity | Spot price | Futures price |
|---|---|---|
| Agricultural | ||
| Cocoa(a) | na | Intercontinental Exchange US |
| Coffee(a) | na | Intercontinental Exchange US |
| Corn | United States Department of Agriculture Grain Export Chicago Yellow Number 2 | Chicago Board of Trade |
| Cotton(a) | na | Intercontinental Exchange US |
| Oats(a) | na | Chicago Board of Trade |
| Rice(a) | na | Chicago Board of Trade |
| Soybeans | United States Department of Agriculture Yellow Number 1 | Chicago Board of Trade |
| Sugar(a) | na | Intercontinental Exchange US |
| Wheat | United States Department of Agriculture Soft Red Winter Number 2 | Chicago Board of Trade |
| Base metals | ||
| Aluminium | London Metal Exchange – Primary Aluminium – Cash |
London Metal Exchange – Primary Aluminium |
| Copper | London Metal Exchange – Cash | London Metal Exchange |
| Lead(a) | na | London Metal Exchange |
| Nickel | London Metal Exchange – Cash | London Metal Exchange |
| Zinc | London Metal Exchange – Cash | London Metal Exchange |
| Energy | ||
| Brent oil(a) | na | Intercontinental Exchange Europe |
| Heating oil(a) | na | New York Mercantile Exchange |
| US natural gas | Henry Hub | New York Mercantile Exchange |
| WTI oil(a) | na | New York Mercantile Exchange |
| Precious metals | ||
| Gold | Bloomberg gold spot price | COMEX |
| Silver | Bloomberg silver spot price | COMEX |
|
(a)No spot prices are reported as these commodities were not used in the Granger causality tests Source: Bloomberg |
||
Footnotes
The authors are from International Department. [*]
For a summary, see G20 Study Group on Commodities (2011, pp 32–33). [1]
The ‘front-month’ contract for a given commodity refers to the futures contract with the nearest expiry date; it is generally the most liquid futures contract and has the smallest spread to the spot price. [2]
Also, institutional factors may create a close relationship between futures and spot prices in some markets, independently of any direct arbitrage relationship. For example, spot or contract prices may be set mechanically with respect to futures prices. [3]
This equation is a variant of Hotelling's rule, which states that in a competitive market, the price of an non-renewable resource (net of marginal costs) will increase in line with the interest rate. [4]
In Equation (1), c and y are expressed as proportions of the spot price for illustrative purposes. [5]
A risk premium would be expected to drive a wedge between futures and spot prices,
particularly if investors are highly risk averse. Intuitively, this risk
premium can be thought of as the compensation required by financial speculators
to participate in the futures market, since their participation is not derived
from a need to hedge an exposure in the physical market. Adding this risk
premium term (which can be positive or negative depending on whether the
desired net position of commodity producers and consumers in the futures
market is short or long) would alter the form of Equation (1) to: 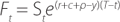 , where ρ is the risk premium.
[6]
, where ρ is the risk premium.
[6]
Speculative price movements could also occur in spot markets. However, such instances are likely to be relatively isolated, as uninformed financial investors (who have no underlying physical demand for commodities) are, in general, less likely to participate in spot markets (where they will incur storage and financing costs without an offsetting convenience yield). While market manipulation by informed participants in spot markets may also be possible, this is unrelated to the financialisation of commodity markets. [7]
More formally, the percentage change in the spot price is regressed on lagged changes in both the spot price and the futures price. If the estimated coefficients on the lagged changes in the futures price are found to be jointly statistically significant (using a Wald test) then changes in the futures price will be said to Granger-cause changes in the spot price. A similar regression is then run for the percentage change in the futures price. Bi-directional Granger causality occurs when both variables are found to Granger-cause each other (i.e. they are jointly determined). If a variable does not help predict the other, no Granger causality is said to exist. [8]
A GARCH model is used because high-frequency financial time series typically exhibit ‘volatility clustering’, whereby large changes in a variable tend to be followed by other large changes and small changes tend to be followed by other small changes. GARCH models explicitly estimate this relationship and in so doing are able to estimate more accurate standard errors than an ordinary least squares approach. The (1,1) specification for the model was selected based on the evidence in Hansen and Lunde (2005) and the Akaike and Schwarz Bayesian Information Criteria. [9]
While industrial production may be a more relevant measure of global activity for this purpose, we use GDP in order to assess the claims made in previous research. Global GDP is measured using purchasing power parity exchange rates and potential output is calculated using the Hodrick Prescott filter (λ = 1,600). [10]
For information on the differences between selected commodity futures price indices, refer to RBA (2011). [11]
The analysis for the latter period was also performed over a slightly longer time period (March quarter 2000 to the December quarter 2011) to test the sensitivity of the results to the use of a relatively short time period. The results from this exercise were very similar to those obtained over the shorter period. [12]
The principal component analysis is performed using percentage changes in quarterly (daily average) front-month futures prices. The exception to this is the use of LME spot prices for base metals from the start of the sample period to July 1997 due to the unavailability of LME futures prices up until this time. The results of the principal component analysis also hold for a (smaller) sample of spot, rather than futures, prices. [13]
The standard Scree test and the criterion developed by Otter, Jacobs and den Reijer (2011) show that there is one significant common factor, while the Bai-Ng Panel Information Criteria suggest one or two common factors, depending on which statistic is used (Bai and Ng 2002). [14]
References
Arbatli E and G Vasishtha (2012), ‘Growth in Emerging Market Economies and the Commodity Boom of 2003–2008: Evidence from Growth Forecast Revisions’, Bank of Canada Working Paper No 2012-8.
Bai J and S Ng (2002), ‘Determining the Number of Factors in Approximate Factor Models’, Econometrica, 70(1), pp 191–221.
Connolly E and D Orsmond (2011), ‘The Mining Industry: From Bust to Boom’, RBA Research Discussion Paper No 2011-08.
Domanski D and A Heath (2007), ‘Financial Investors and Commodity Markets’, BIS Quarterly Review, March, pp 53–67.
Dwyer A, G Gardner and T Williams (2011), ‘Global Commodity Markets – Price Volatility and Financialisation’, RBA Bulletin, June, pp 49–57.
Fattouh B (2011), ‘An Anatomy of the Crude Oil Pricing System’, The Oxford Institute for Energy Studies No 40.
Frankel JA and AK Rose (2009), ‘Determinants of Agricultural and Mineral Commodity Prices’, in R Fry, C Jones and C Kent (eds), Inflation in an Era of Relative Price Shocks, Proceedings of a Conference, Reserve Bank of Australia, Sydney, pp 9–43.
G20 Study Group on Commodities (2011), ‘Report of the G20 Study Group on Commodities under the Chairmanship of Mr Hiroshi Nakaso’, November. Available at <http://www.banque-france.fr/fileadmin/user_upload/banque_de_france/Economie_et_Statistiques/ Tendances_Regionales__ne_pas_ecraser_/mois_impairs/Study_group_report_final.pdf>.
Hansen PR and A Lunde (2005), ‘A Forecast Comparison of Volatility Models: Does Anything Beat a GARCH(1,1)?’, Journal of Applied Econometrics, 20(7), pp 873–889.
Inamura Y, T Kimata, T Kimura and T Muto (2011), ‘Recent Surge in Global Commodity Prices – Impact of Financialization of Commodities and Globally Accommodative Monetary Conditions’, Bank of Japan Review, 2011-E-2.
Kosev M and T Williams (2011), ‘Exchange-traded Funds’, RBA Bulletin, March, pp 51–59.
Otter PW, JPAM Jacobs and AHJ den Reijer (2011), ‘A Criterion for the Number of Factors in a Data-rich Environment’, University of Groningen, unpublished manuscript, February. Available at <http://www.eco.rug.nl/medewerk/jacobs/jjdownload/CriterionForNumberOfFactors_Feb2011.pdf>.
RBA (Reserve Bank of Australia) (2011), ‘Box A: A Comparison of Commodity Indices’, Statement on Monetary Policy, November, pp 14–16.
Reichsfeld DA and SK Roache (2011), ‘Do Commodity Futures Help Forecast Spot Prices?’, IMF Working Paper WP/11/254.
Shleifer A and LH Summers (1990), ‘The Noise Trader Approach to Finance’, The Journal of Economic Perspectives, 4(2), pp 19–33.