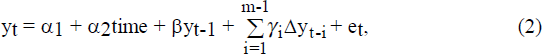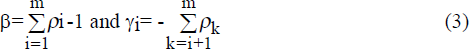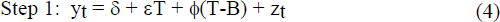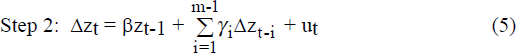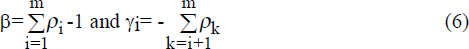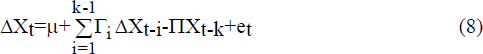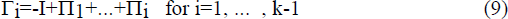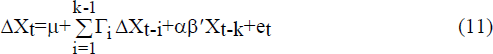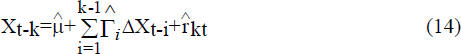RDP 9314: The Demand for Money in Australia: New Tests on an old Topic Appendix 2: Test Procedures

Standard Unit Root Tests

If the series, y, is drawn from the m-order autoregressive process,

then it is stationary and integrated of order zero if the absolute value of 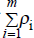is less than unity. If it is equal to unity, then the series possesses a unit root and is non-stationary and integrated of order one.

The augmented Dickey-Fuller (ADF) test is a standard test for the existence of a unit root and is estimated in the form,

where

The null hypothesis is that a unit root exits, β=0, and the alternative is that the series is stationary, β<0. The standard t-ratio tests do not apply, with critical values taken from Fuller (1976). The lagged dependent variables represent higher order auto-regressive processes of y, with the lag order selected in order to eliminate serial correlation (based on Lagrange multiplier tests). If lags of the dependent variable are not included, equation (2) reduces to the Dickey-Fuller (DF) test equation. A time trend is also included in equation (2) to test for the presence of a deterministic trend. The critical values for the constant and trend in the ADF equation are drawn from Tables I, II and III of Dickey and Fuller (1981).

Phillips' (1987) Z_t test procedure is a non-parametric adjustment of the t-statistic of the unit root variable in the DF test equation. It includes a weighted average of lagged covariances of the error term, the truncation for which can be based on the number of significant sample autocorrelations of the first-differenced variable, or arbitrarily set to 5 and 10 and testing for other lag truncations only if the outcomes vary (Leong and Ouliaris (1991)). The latter method is applied in this paper. The limiting distribution for Z_t is identical to that of the ADF statistic.

Unit Root Tests in the Presence of a Broken Trend

Following Perron (1989), a two-step procedure for testing for unit roots in the presence of a break in the slope of the trend is used:

where T indicates a time trend and B is the time value of the break with T−B=0 for T<B, and

where

The ‘m’ lags are selected on the basis of Lagrange Multiplier tests for serial correlation. The critical value for β is taken from Table V.B on page 1377 of Perron (1989) and varies with L, the time of the break relative to the sample size. For example, the 5-lag ADF statistic for the money base with break date at 1982:2 is −4.543. The critical value with an L of 0.6 (rounded-up from 0.58=50/87) is −3.95 at the 5 per cent level and −4.57 at the 1 per cent level, and so the money base is stationary around a broken trend at 1982:2 at the 5 per cent level.

Engle-Granger Test for Cointegration

Engle and Granger (1987) set out a well-known and simple residual-based test for cointegration, where the residuals of the estimated hypothesised long-run relationship are tested for a unit root using the ADF procedure. The critical values are drawn from Phillips and Ouliaris (1990).

Johansen Test for Cointegration

Johansen (1988) and Johansen and Juselius (1990) set out a maximum likelihood procedure for the estimation of the cointegrating vectors in the VAR system and which enables tests for the number of cointegrating vectors. Suppose the vector of p variables, X_t=(X_{1t, … ,}X_pt)′, is generated by the k-order vector autoregressive process,

where µ is a vector of constants, Π_i are pxp coefficient matrices and e_t is independently and identically normally distributed with a mean and variance, (0,Λ). This process may be rewritten without loss of generality as

where

and

The matrix Π contains the long-run information in the system and is analogous to the error-correction representation of Engle and Granger (1987). There are three scenarios of interest concerning the rank of Π:

Case 1 If rank(Π)=r where r=0, then Π is a null matrix and there is no long-run relationship between the I(1) variables under consideration. As such, there is no cointegrating relationship between the variables and the system is properly estimated as a VAR system in first differences;

Case 2 If rank(Π)=r where 0<r<p, then there are r cointegrating vectors. The linear combinations of the rows (or columns) of Π span r dimensions in p space; and

Case 3 If rank(Π)=r where r=p, then Π has full rank and there are p independent linear combinations between the variables under consideration and they span all dimensions in p space. This indicates that all the variables are individually I(0) and so the system is properly estimated as a VAR in levels.

If there is cointegration then the coefficient matrix Π can be decomposed as αβ′ where α and β are matrices of dimension pxr. Equation (8) may be rewritten as

where β contains the cointegrating vectors such that the rows of β′ create linear combinations of the elements in X_t-k which are stationary. The matrix α contains the loading vectors. The loading vectors may be interpreted analogously to the coefficient on the error-correction variable in the ECM of Engle and Granger (1987).

Johansen (1988) and Johansen and Juselius (1990) develop a maximum likelihood estimation procedure for µ, Γ_i, α, β and Λ and also provide tests for the number of cointegrating vectors. The lagged ΔX_t−i and µ in (11) are stacked in a vector Z_1t with the parameter coefficients arranged in the matrix Γ. The model may be rewritten as

Regressing ΔX_t and X_t−k on Z_1t using OLS yields matrices of the residuals 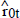and ,

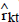These residuals represent the variables ΔX_t and X_t−k after the removal of short-run dynamics and constant terms. Using these residuals, the likelihood function can be concentrated and estimates of α, µ, Γ and Λ can be found as functions of β.

Three product moment matrices of these residuals, S_ij, are calculated as

for i,j=0,k and T being the number of observations.

Johansen shows that the likelihood-maximising solution for 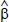is found by solving the eigenvalue problem

This results in the eigenvalues 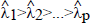. The estimate of β is obtained as the normalised eigenvector associated with the relevant eigenvalue. Estimation of the remaining parameters is done by substituting 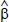for β in the functions obtained from the concentrated likelihood function.

There are two likelihood ratio tests which test the number of stationary combinations of the variables under consideration. The maximum eigenvalue test, or ‘lambdamax’ for short, tests the null hypothesis of r cointegrating vectors against the alternative of r+1 cointegrating vectors. It is given as

where the 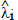are the eigenvalues obtained from estimating 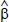. The second likelihood ratio test statistic is the trace test which tests the null that there are at most r cointegrating vectors against the alternative that all the series are stationary, namely that r=p. The trace test statistic is given as

Critical values are provided in Table D2, Osterwald-Lenum (1992). The maximum likelihood procedure developed by Johansen and Juselius also allows for linear restrictions on α and/or β to be tested.