Research Discussion Paper – RDP 2022-06 Do Australian Households Borrow to Keep up with the Joneses?
1. Introduction
There has been increasing academic and policy interest in the effect of inequality on both microeconomic and macroeconomic outcomes. One aspect that has received attention in the literature is the potential for local inequality to affect indebtedness and credit allocation. A number of papers have found that a high level of local inequality leads to increased levels of indebtedness, as households appear to try to ‘keep up’ with the income and consumption of their wealthier neighbours (e.g. Georgarakos, Haliassos and Pasini 2014; Berlemann and Salland 2016). This has potential important implications for both financial and macrofinancial stability if this ‘keeping up with the Joneses’ leads households to become overextended, and more sensitive to negative shocks. Other papers have argued that local inequality can limit the allocation of credit to lower income households in a region if banks assess them relative to their local peers and have geographic caps on lending (Coibion et al 2020; Loschiavo 2021). Such screening effects can lead to an inefficient allocation of credit and entrench inequality.
In this paper, I examine the effect of local income inequality on debt using Australia as a case study. Australia shares many similar economic and financial conditions with the United States and Europe, the focus of existing literature, but with much higher levels of household debt. Most analysis on income inequality in Australia has focused around the national level, which has remained broadly flat in the past decade (Productivity Commission 2019). The long streak of uninterrupted economic growth in Australia has brought significant improvement in income for the average Australian household in every income decile, in contrast with the United States where income inequality increases at a similar rate as Australia but the distribution is much more uneven (Productivity Commission 2019). However, aggregate inequality masks variation at the local level, which may serve as a key reference group for most individuals when making decisions. The significant spatial and temporal variation at the local level makes Australia an interesting case study.
I find evidence of ‘keeping up with the Joneses’-type dynamics in Australia. Specifically, there is a significant positive association between local income inequality and household investment debt. The accumulation of investment debt is mainly driven by middle-aged and middle-income mortgage holders without liquidity and borrowing constraints and who are willing to take financial risk. Car debt also increases moderately with a rise in local inequality, driven by middle-aged outright home owners who self-perceive as financially prosperous. The accumulation of car debt lends evidence to the traditional ‘conspicuous consumption’ channel, with households trying to close consumption gaps in a conspicuous manner. On the other hand, the accumulation of investment debt suggests an additional channel for the ‘keeping up with the Joneses’ hypothesis – households borrow to invest, in the hope of keeping up with a rising local income gap. Such a channel could be particularly concerning if the households that take on the additional risky investments were financially fragile. However, in Australia it appears that they are taken on by households that are financially comfortable, lessening such concerns.
The paper directly relates to the literature examining the relationship between household indebtedness and income inequality. One strand of this literature identifies positive peer effects on borrowing, suggesting a ‘demand’ channel. This relates to the well-known ‘keeping up with Joneses’ phenomenon often cited as an explanation for households' excess of labour supply and overspending in the United States (Stiglitz 2012). According to this hypothesis, which goes back to Veblenʼs theory of conspicuous consumption, an increase in income inequality prompts lower-income groups to spend or borrow more in trying to imitate the consumption patterns of higher-income groups. Georgarakos et al (2014) show that Dutch households who consider themselves poorer than their reference group borrow more. Similarly, Berlemann and Salland (2016) find positive effects of the local average income on debt market participation using German banking data. Another strand in the literature supports the ‘supply’ channel in which creditworthiness is private information and local income inequality serves as a ‘signal’ to screen borrowers. This leads to credit being more readily accessible to high-income households in more unequal areas, as found by Coibion et al (2020) using US credit data. Likewise, Loschiavo (2021) shows that the probability of being indebted is higher for high-income Italian households in high-inequality areas compared with equivalent households in lower-inequality areas, suggesting that as local inequality increases banks are more likely to use a household's position in the income distribution as a measure of creditworthiness.
This paper contributes to the literature in several ways. First, I explore the effects of changes in local income inequality on not only total household debt but also its composition, including mortgage debt and different types of non-mortgage debt. Second, I examine the heterogeneity of the effects across different cohorts based on demographics and financial capacity, which, to my best knowledge, has not been done in the literature before. The very rich micro data on Australian households from the Household, Income and Labour Dynamics in Australia (HILDA) Survey, which includes questions on the details of household balance sheets, allows for this granularity. By exploring the composition of debt, as well as the heterogeneous effects across household types, I shed substantial additional light on the mechanisms and macroeconomic implications of the relationship between local inequality and household borrowing.
2. Local Income Inequality in Australia
To illustrate local variation in income inequality, I map the Gini coefficient within each Statistical Area 3 (SA3) area for Australia, Greater Sydney and Greater Melbourne in 2018 (Figure 1).[1],[2] While the aggregate Gini coefficient is roughly 0.4, local Gini coefficients range from 0.35 to 0.7 with a standard deviation (SD) of 0.05. Income inequality appears relatively high in mining areas and major cities. This is unsurprising since the mining industry generally pays more than other regional industries, but at the same time employs fewer people in the region. On the other hand, there is a greater spread of occupations available in metropolitan areas, from lower-wage services industries, to high-wage professional services. The map of Greater Sydney, for instance, reveals that income inequality in the northern and eastern suburbs is much higher than in the west and south west of Sydney.
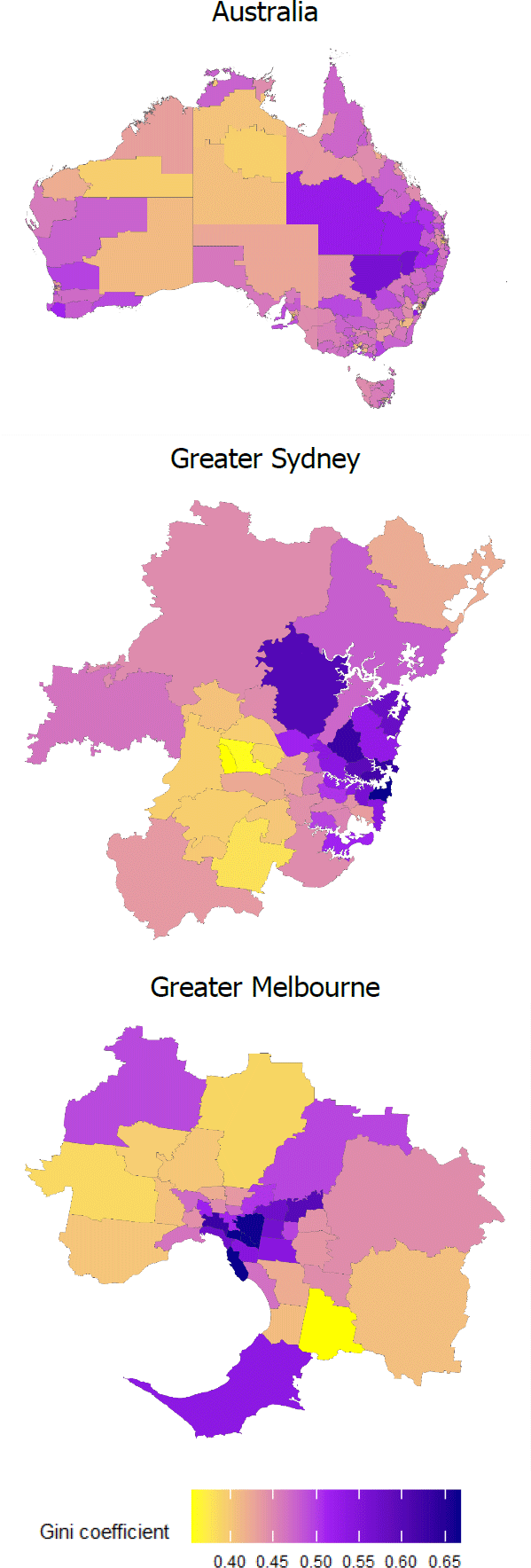
Note: Areas without SA3 codes in white and SA3 areas with missing values for Gini coefficient in grey.
Sources: ABS; Author's calculations
Next I look at how the distribution of income inequality across SA3 areas has changed over time. Figure 2 illustrates that for NSW from 2010 to 2018. What stands out is the effect of the mining boom in Bourke–Cobar–Coonamble and Upper Hunter, for instance, which resulted in a substantial increase in income inequality in those areas from 2010 to 2014 (a roughly 2 SD increase in the Gini coefficient). The end of the mining boom saw this inequality level drop significantly in 2018, to even lower than the 2010 level for some regions.
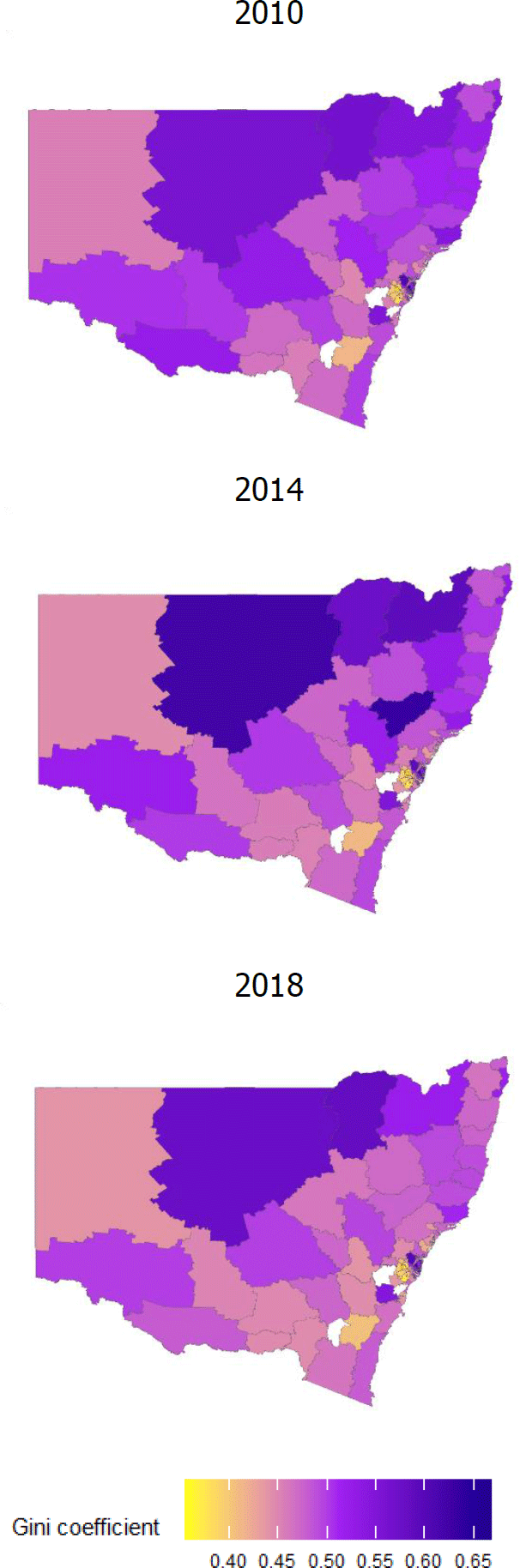
Note: Areas without SA3 codes in white and SA3 areas with missing values for Gini coefficient in grey.
Sources: ABS; Author's calculations
In contrast, the tourism industry experienced softer conditions in the years following the global financial crisis (GFC), reflecting the high exchange rate (Khandaker and Islam 2017). This appears to have led to a reduction in income inequality in areas that are tourism centric (for instance, Cottesloe and Uluru). However, from the mid-2010s to the onset of the COVID-19 pandemic, conditions facing the industry have become more favourable, supported by the depreciation of the Australian dollar (Dobson and Hooper 2015). This is reflected in a pick-up in income inequality in those regions. Thus, there is evidence for both the variation in inequality across small areas in Australia and also variation over time within areas.
But is there a link between the degree of inequality in the regional income distribution and household indebtedness? Figure 3 plots total household debt in real monetary terms against the Gini coefficient for each SA3 region. The positive correlation between the two measures is quite apparent, both before and after the GFC, suggesting that household debt is generally higher in regions with a higher degree of income inequality. While these correlations are interesting, they could be driven by numerous factors. For example, areas with greater inequality might also have higher average income, and it may be that the higher incomes account for the higher total debt. Similarly, as highlighted above, in areas with large, cyclical industries such as mining and tourism, the degree of inequality may be procyclical, as may be debt. Therefore, to assess the effect of local income inequality on the debt-taking behaviour of Australian households, I have to employ a regression approach at the household level.
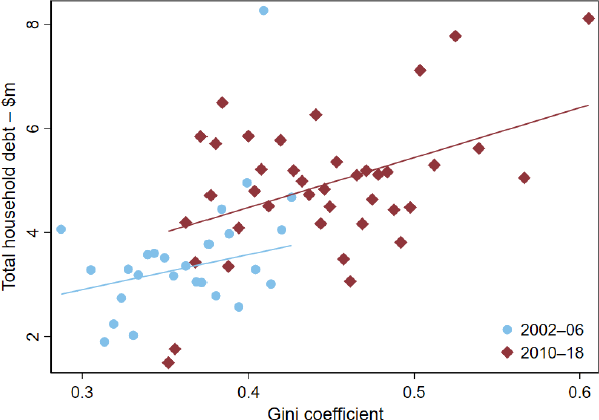
Notes: The figure is a binscatter, where an observation is an SA3–year. Each line represents the linear fit of the relationship between total household debt and Gini coefficient using OLS, for the respective sampling period.
Sources: ABS; Author's calculations; HILDA Survey Release 19.0
3. Data and Descriptive Statistics
The dataset employed in this study is the Household, Income and Labour Dynamics in Australia (HILDA) Survey Release 2019, an annual longitudinal survey of approximately 8,000 households that is designed to be representative of the Australian population. The survey has asked detailed questions relating to household finances, such as household net worth and debt portfolio, every four years since 2002. The unrestricted version of the survey also includes household location information at an SA3 level, which I use to match with SA3-level income inequality and other macroeconomic measures.
The very detailed wealth modules in the HILDA Survey allow me to construct household total debt and examine its composition. I categorise debt into: mortgage debt, consumer debt (non-mortgage, including credit card and personal debt, e.g. hire purchase loan, car loan and other personal loans) and investment debt (e.g. bonds, shares and currencies). While questions about total debt and home debt were asked in all five wealth modules, those concerning consumer debt and investment debt were only asked from 2006 onwards.
The measure of local income inequality comes from ABS estimates of personal income in small areas. The ABS data allow for estimation of the Gini coefficient and the top 10 per cent share of total personal income at the SA3 level. Using this measure of income inequality data, rather than constructing it using the microdata, helps limit direct feedback within the regression, which could be driven, for example, by outlier observations.
The choice of SA3 level stems from a number of considerations. First, SA3s closely align to Local Government Areas, whose average income and income inequality are most regularly reported by the media, and so they may be most likely to be the relevant metric when households compare themselves to others. Second, a number of relevant macroeconomic controls are available at the SA3 level. Third, SA3s appear to provide the right balance between having a large number of individual areas, with good local control variables, and not having issues around having too small samples of households for robust analysis.
I also restrict the sample to the post-GFC period (2010 to 2018) for several reasons: 1) to control for potential structural breaks in the distribution of income inequality and in the financial landscape due to the GFC; 2) the ABS estimates of personal income in small areas are not comparable before and after 2007 (ABS 2022); and 3) to use only one sample across different types of debt (consumer debt and investment debt are only available from 2006) for more direct comparison of the estimates.
Moreover, I keep only households that exist in at least two consecutive wealth modules and do not move out of their initial SA3 region. I focus on this subset as households may choose to move closer to their ‘reference group’, leading to some direct feedback between (changes in) local inequality and debt for these households (Guerrieri, Hartley and Hurst 2013; Coibion et al 2020). To follow as many households as possible over time, I follow Price, Beckers and La Cava's (2019) procedure to merge households and determine household heads.[3] This gives me an unbalanced panel of 5,483 unique households (12,605 observations) over three survey waves, from 2010 to 2018.
Table 1 presents household demographic and financial statistics of the sample over the three survey years. The household demographics remain stable over the waves with approximately 60 per cent of household heads being male and 60 per cent married. The mean age of household heads is roughly 52 years old and on average households have two children. Around 30 per cent of household heads have a university degree and 60 per cent are employed. Turning to household financial positions, while the mean gross income grew steadily at around 2 to 3 per cent per annum, growth in housing wealth and household debt fluctuated over time. Post-GFC self-reported home values declined before picking up significantly between 2014 and 2018, while mortgage debt kept increasing over the period. On the other hand, both consumer debt and investment debt have declined since 2010. Overall, the full, unrestricted sample appears similar (see Table A1).
| 2010 | 2014 | 2018 | |
|---|---|---|---|
| Household variables (from HILDA Survey Release 19.0) | |||
| Age (years) | 52.6 | 52.4 | 51.9 |
| Male (%) | 59.3 | 59.3 | 57.6 |
| Married (%) | 61.1 | 60.3 | 57.0 |
| Number of children (if having children) | 1.8 | 1.8 | 1.8 |
| University graduate (%) | 28.2 | 34.9 | 36.3 |
| Labour force (%) | 64.3 | 65.3 | 64.9 |
| Employed (%) | 62.2 | 63.3 | 62.6 |
| Home owner (%) | 76.4 | 71.1 | 67.2 |
| Gross income ($'000) | 87.4 | 90.1 | 88.9 |
| Net worth ($'000) | 877.9 | 847.1 | 942.6 |
| Financial wealth ($'000) | 315.9 | 349.8 | 378.2 |
| Total debt ($'000) | 164.2 | 169.7 | 169.5 |
| Mortgage debt ($'000) | 129.7 | 140.5 | 142.7 |
| Home debt ($'000) | 96.2 | 101.4 | 102.5 |
| Other property debt ($'000) | 33.5 | 39.1 | 40.2 |
| Non-mortgage debt ($'000) | 34.5 | 29.3 | 26.8 |
| Credit card debt ($'000) | 2.2 | 1.6 | 1.4 |
| Hire purchase debt ($'000) | 0.3 | 0.2 | 0.2 |
| Car debt ($'000) | 1.6 | 1.8 | 1.9 |
| Business debt ($'000) | 7.9 | 9.5 | 7.3 |
| Investment debt ($'000) | 7.8 | 4.5 | 3.8 |
| No of observations | 4,197 | 5,790 | 6,123 |
| SA3 macroeconomic variables (from ABS and Corelogic) | |||
| Gini coefficient (index point) | 0.466 | 0.458 | 0.456 |
| Median house price ($'000) | 397 | 435 | 533 |
| Unemployment rate (at SA4 level, %) | 4.8 | 6.6 | 5.0 |
|
Sources: ABS; Author's calculations; Corelogic; HILDA Survey Release 19.0 |
|||
4. Empirical Methodology
To examine the relationship between debt and local income inequality, I estimate the effects of a change in local income inequality on household debt accumulation using a simple reduced-form regression. The reduced-form approach is common in the literature (Coibion et al 2020; Loschiavo 2021) and introduces a number of potential threats to identification. First, the existing literature has shown that household indebtedness is a function of both the supply of and the demand for credit (Cox and Jappelli 1993; Duca and Rosenthal 1993; Browning, Gørtz and Leth-Petersen 2013). The former is driven by household characteristics that the financial institutions consider to determine credit worthiness, while the latter also depends on household preferences, which are generally unobserved. Omitting household characteristics that affect debt accumulation, both observed and unobserved, may bias the estimated effects of local inequality on debt. Second, the supply of and demand for credit is also a function of region-specific macroeconomic and credit conditions that potentially correlate with local income inequality, such as housing prices. As such, omitting these factors could lead to biased estimates. Third, there is a potential reverse causality between debt accumulation and income inequality. Finally, households' mobility choices create a potential selection bias. In this section I discuss in detail the empirical strategies to address these identification concerns.
I first estimate the following baseline regression:
where is the debt accumulated between t and t–4 by household i who resides in local area c, measured as a share of household income in t–4. is the change in local income inequality between t and t–4 in local area c, measured in Gini coefficients. is a vector of covariates included to control for time-varying household demographics (e.g. age, education, employment of household head), household structure (e.g. marital status, number of children, number of household members) and household finances (e.g. income, housing wealth, non-housing financial wealth, liquidity). Macro covariates control for time-varying regional measures of housing prices, unemployment rates, income and debt, while Iict represents regional time trends, where Iic indicates the SA3 area of household i. All time-varying controls are in lags (t–4) and first differences (between t and t–4). The coefficient of interest is , which traces the relationship between a 1 SD increase in Gini coefficient and debt accumulation as a share of income.
I run the regression in first differences to focus on the within-household variation and control for unobserved time-invariant household characteristics such as risk preferences, time preferences and financial literacy, which have been shown to govern household demand for credit and portfolio choices (Browning et al 2013). As such, the approach eliminates concerns regarding omitted time-invariant household-specific factors. It also enables easy interpretation of the heterogeneous effects of local income inequality across different demographic and financial groups.
The macro covariates account for temporal variation in debt accumulation due to changes in macroeconomic and credit conditions over time. I include several such covariates to account for factors that are known to affect debt accumulation, such as the economic cycle and housing prices. I also include a region-specific linear time trend Iict to help account for other temporal variation, such as changes in the financial regulations and lending standards, as well as borrowing patterns that are specific to the regions. The rich set of observable household characteristics included in control for much of the remaining within-household variation that governs the supply of credit. Taken together, these factors should help to account for other factors that could drive both income inequality and debt accumulation.
Importantly, there are still potential issues around reverse causality. That is, changes in household indebtedness could lead to changes in local income inequality. This would be more concerning if the focus was on wealth or consumption inequality, as both can be affected by household portfolio choices. However, it is less of a concern for income inequality. In particular, income inequality is not dependent on debt accumulation that is wealth generating (housing debt), or debt that services consumption (car debt and credit card debt). And while investment debt may generate dividend income and investment property debt may generate rental income, these sources of income constitute a negligible proportion (0.3 per cent) of personal income measure used by the ABS to construct inequality.[4]
Still, it is worth considering how such reverse causality could bias the results. If there is a systematic increase in investment debt from the lower end of the distribution, it may, in turn, lower income inequality. As such, there should be a negative feedback from investment debt to inequality. By contrast, if investment debt accumulation is driven by the top of the distribution, it could aggravate income inequality, resulting in a positive relationship between the two. Finally, if the recipients of extra investment income from investment debt are in the middle of the distribution, the change in Gini coefficient will be minimal (Gastwirth 2017). Heterogeneity analysis across the income distribution would shed light on the direction of the bias caused by reverse causality.
As noted before, another econometric issue may arise if households choose to move closer to their reference group, making local inequality endogenous to household debt for households that move out of their initial local region. To eliminate this source of endogeneity, I estimate Equation (1) on the sample of households that do not move out of their initial SA3 region throughout the entire observation period. However, the non-moving households may not be a random sample, which introduces selection bias. I address this concern using a Heckman selection model in the robustness section.
Even after accounting for all these potential biases, it is worth noting that the empirical model does not establish causality as there could still be some unobserved time-varying factors at the local level that I cannot fully control for. As such, the estimates are more suggestive of a relationship, rather than sharply identifying the causal effects of local income inequality on household debt. The non-causal evidence is, nevertheless, useful to understand the mechanisms that potentially drive this relationship.
To better understand the mechanisms and implications behind any relationship between local income inequality and household debt, I perform two extensions. First, I re-run the baseline model for different components of household debt. Second, to look at heterogeneous effect across households I modify the model specification to allow for the interaction between inequality and household characteristics:
where Groupic,t–4 indicates the demographic or financial group the household belonged to in previous period, which reduces concerns about feedback from household behaviour to their characteristics. I explore heterogeneous effects of local income inequality along several dimensions: income ranking and financial prosperity, life cycle and housing status, and financial constraints and attitude.
Importantly, the heterogeneity in debt accumulation across demographic and financial groups may be driven by the heterogeneous effects of other macro factors, which are loaded onto inequality if not controlled for. For instance, changes in local housing prices are more likely to relax credit constraints for lower income households, and so have a larger effect on their debt accumulation. To isolate the variation due to changes in local income inequality, I control for the interactions between the SA3-level macro covariates and household characteristics.[5]
5. Results and Discussion
5.1 Baseline results
In this section, I discuss the baseline results from estimating Equation (1). Table 2 presents the estimated effects of a 1 standard deviation increase in Gini coefficient on the accumulation of total debt and different types of debt.[6] Looking at debt as a share of income allows me to assess the economic significance of the estimates and enables easy and robust interpretation of the heterogeneous effects across sub-populations with different levels of income and debt in later sections.[7]
| Total | Mortgage | Non-mortgage | |||
|---|---|---|---|---|---|
| Total | Home | Other property | |||
| Gini coefficient | −0.46 (7.48) |
−8.61 (6.00) |
−4.13 (4.18) |
−4.47 (7.41) |
6.28*** (2.32) |
| No of observations | 7,631 | 7,631 | 7,631 | 7,631 | 7,631 |
| Non-mortgage | |||||
| Credit card | Hire purchase | Car | Business | Investment | |
| Gini coefficient | −0.22 (0.19) |
−0.01 (0.10) |
0.50* (0.27) |
1.42 (2.06) |
3.32*** (1.14) |
| No of observations | 7,631 | 7,631 | 7,631 | 7,631 | 7,631 |
| Household covariates | Y | Y | Y | Y | Y |
| SA3 covariates | Y | Y | Y | Y | Y |
| SA3 time trends | Y | Y | Y | Y | Y |
|
Notes: Clustered standard errors at SA3 level are in parentheses. ***, ** and * denote statistical significance at the 1, 5 and 10 per cent levels, respectively. Sources: ABS; Author's calculations; HILDA Survey Release 19.0 |
|||||
The estimated effect of local income inequality on total household debt is negligible. The effects on home debt and other property debt are not statistically significant and the magnitudes small relative to the standard size of a mortgage. While an 8 percentage point response seems relatively large, on average mortgage debt is equivalent to 100 per cent of income, and represents more than 300 per cent of income for the top 10 percentile of debt-to-income ratios.
The effect on non-mortgage debt appears to be mostly driven by investment debt, which is both statistically and economically significant. A 1 SD increase in the Gini coefficient is associated with a little more than a 3 percentage point increase in the ratio of investment debt to income. For context, this is equivalent to the mean ratio in the sample. Business debt also increases but the estimate is not statistically significant.
Among types of consumer debt, only car debt significantly increases as the local inequality rises, with the standardised increase being around 0.5 percentage points. This compares to a mean ratio of car debt to income of 2 per cent.
Overall, the statistically and economically significant positive effects of local income inequality on investment debt and car debt are suggestive of the credit demand channel.[8] While accumulation of car debt is consistent with traditional status signalling and trying to close consumption gaps, the accumulation of investment debt suggests an alternative interpretation of ‘keeping up with the Joneses’. That is, as income inequality rises in the local area, households may try to close the income gap with their neighbours by taking out more debt for the purpose of non-residential investment.
Nevertheless, to better understand the mechanisms and economic implications, it is important to understand which households drive the results. For instance, households at the upper end of the income distribution may not have much incentive to keep up. Therefore, if they drive the average debt accumulation, that could suggest the credit supply channel rather than the credit demand channel. Also, there may be financial or macroeconomic stability concerns if lower-income households or those with liquidity and credit constraints exhibit such debt-taking behaviour, in contrast with middle- and higher-income households who have a better ability to weather shocks. Finally, life cycle and housing status can inform us about the priorities in demand for debt, while willingness to take financial risk potentially motivates demand for investment debt.
In the next sections, I assess the mechanisms and the economic implications of local income inequality by estimating the heterogeneous accumulation of investment and car debt across key demographic and financial groups with Equation (2).
5.2 Income and financial prosperity
Table 3 (Panel A) presents the effects of a 1 standard deviation increase in Gini coefficient on investment and car debt accumulation by households in each local income quartile. Their weighted average constitutes the estimated effect in Table 2. I find that households in the middle-to-upper end of the local income distribution (the third quartile) increase their investment debt by 12 percentage points as a share of income, driving much of the overall effect on investment debt. By contrast, accumulation of investment debt by the bottom and top quartiles are neither statistically nor economically significant. These results reinforce the role of the demand channel, as investment debt accumulation is driven by households who have both the means and the desire to keep up with their richer neighbours and close the income gap. The heterogeneity in accumulation of car debt follows similar but more subdued patterns. Importantly, in both cases the results suggest limited concern for macrofinancial stability as these households are likely to be in a better position to weather shocks.
It is important to reiterate that I define income quartiles based on the local income distribution, rather than the national distribution. As such, households in the third quartile may still have low incomes by national standards. Nevertheless, if I categorise households by their positions in the national income distribution the results are similar (Table B9), with the third quartile driving the response (the third quartile has incomes ranging between $77,000 and $120,000).
Another potential limitation of using local income ranking is that households do not necessarily know where they stand exactly in the local income distribution. While inequality in the region could be reasonably common knowledge, households may perceive their relative position differently from a mechanically constructed income ranking. To the extent that this self-perceived position drives their demand for debt, particularly one that helps boost their future earnings, it is important that we assess the heterogeneity along this dimension. HILDA Survey data enable this assessment by asking households to self-evaluate their prosperity given current needs and financial responsibilities, with answers ranging from ‘very poor’ to ‘prosperous’.[9]
Table 3 (Panel B) shows that households who feel ‘reasonably comfortable’ have the largest increase in investment debt following an increase in local inequality, consistent with results observed for middle-income earners. Unsurprisingly, accumulation of car debt is notably stronger among households who identify as financially prosperous, perhaps indicating their desire to signal their social status via conspicuous consumption, despite being in the middle of the actual income distribution.
| Investment | Car | |
|---|---|---|
| Panel A: Local income ranking in t–4 | ||
| 1st quartile | 0.94 (0.92) |
0.64 (1.58) |
| 2nd quartile | 0.43 (1.05) |
0.01 (0.35) |
| 3rd quartile | 12.35** (4.93) |
1.13** (0.48) |
| 4th quartile | 1.05 (0.92) |
0.47 (0.36) |
| No of observations | 7,631 | 7,631 |
| Panel B: Self-perceived financial prosperity in t–4 | ||
| Very poor | 2.55 (1.57) |
4.27 (3.49) |
| Poor | 1.41*** (0.45) |
0.71 (0.69) |
| Just getting along | 1.38** (0.66) |
−1.87 (1.97) |
| Reasonably comfortable | 6.65** (2.90) |
1.29 (0.91) |
| Very comfortable | 2.04 (1.91) |
0.93*** (0.36) |
| Prosperous | −0.37 (3.37) |
2.61*** (0.55) |
| No of observations | 6,952 | 6,952 |
| Household covariates | Y | Y |
| SA3 covariates | Y | Y |
| Group × SA3 interactions | Y | Y |
| SA3 time trends | Y | Y |
|
Notes: Clustered standard errors at SA3 level are in parentheses. ***, ** and * denote statistical significance at the 1, 5 and 10 per cent levels, respectively. Sources: ABS; Author's calculations; HILDA Survey Release 19.0 |
||
5.3 Life cycle and housing status
Next I look at the heterogeneity over the life cycle of the household heads. Table 4 (Panel A) presents the estimates where households are distinguished by the age of the household head: 20–39 years of age, 40–64 years of age and 65 years of age and older. I find a significantly stronger effect of local income inequality on the accumulation of both investment debt and car debt for middle-aged (40–64) households. By contrast, younger and older households are less likely to adjust their debt holdings following a change in local inequality. These results broadly align with the earlier results, given middle-aged households are likely to have higher incomes, more established savings and balance sheets (relative to younger households). They are also consistent with life-cycle theories of investing, with older households generally expected to be less risk-taking in their investment strategies.
Consistent with these findings, households with a mortgage, who are mostly middle-aged, take out relatively more investment debt following a change in income inequality (Table 4, Panel B). Outright home owners have a reasonably small response in terms of investment debt, consistent with earlier findings for older households (who are more likely to be outright home owners). And renters, who are more likely to be younger, barely change their behaviour. The heterogeneous effects on car debt are less evident.
| Investment | Car | |
|---|---|---|
| Panel A: Life cycle in t–4 | ||
| 20 ≤ Agei,t–4 ≤ 39 | 0.97 (1.08) |
−0.95 (1.20) |
| 40 ≤ Agei,t–4 ≤ 64 | 5.65*** (1.81) |
1.41*** (0.54) |
| Agei,t–4 ≥ 65 | 0.17 (0.76) |
0.48 (0.48) |
| No of observations | 7,395 | 7,395 |
| Panel B: Housing tenure in t–4 | ||
| Renters | 0.38 (0.44) |
−0.57 (1.46) |
| Mortgagors | 8.79** (3.47) |
0.89 (0.89) |
| Outright home owners | 3.88 (3.16) |
1.06 (0.73) |
| No of observations | 5,958 | 5,958 |
| Household covariates | Y | Y |
| SA3 covariates | Y | Y |
| Group × SA3 interactions | Y | Y |
| SA3 time trends | Y | Y |
|
Notes: Clustered standard errors at SA3 level are in parentheses. ***, ** and * denote statistical significance at the 1, 5 and 10 per cent levels, respectively. Sources: ABS; Author's calculations; HILDA Survey Release 19.0 |
||
5.4 Financial constraints and attitude
Financial constraints and financial behaviour are often associated with household debt-taking behaviour (Johnson and Li 2010; Kreiner, Lassen and Leth-Petersen 2019). In this section, I examine whether accumulation of debt following changes in local income inequality differs based on measures of financial constraints. This is important to look at as there are concerns that constrained households could overextend themselves in trying to keep up with their neighbours. To measure constraints, first I follow Kaplan, Violante and Weidner (2014) to define the liquidity constrained (hand-to-mouth) as households that either carry no liquid wealth or have borrowed up to their credit limit at the end of the pay period. Hand-to-mouth households make up 15 per cent of the sample and are mostly younger to middle-aged, lower income and renters. This is in contrast with the United States where more than one-third of households are hand-to-mouth (Aguiar, Bils and Boar 2020). I also look at whether households would have difficulty raising money for an emergency, which captures credit and liquidity constraints.[10] In this section I also assess the role of financial attitudes by looking at household's willingness to take financial risk with their spare cash.[11] This is interesting, as it provides another lens to look at the role of credit demand versus credit supply in driving the results.
Table 5 (Panel A) shows that households that are not liquidity constrained (that is, who are not hand-to-mouth) take out larger loans for investment purposes than their liquidity-constrained counterparts. Similarly, rising local income inequality substantially changes debt-taking behaviours of households who are able to raise emergency funds easily (Table 5, Panel B). These findings suggest that constrained households are unable or unwilling to take on more debt for investment purposes, and are generally consistent with the earlier results based on incomes.
The differential accumulation of investment debt by financial attitude is even more striking, though not surprising. It highlights that only households willing to take financial risk borrow more for investment, following an increase in local inequality (Table 5, Panel C). As non-residential investment is a high risk–high return venture, this result lends further support to the theory that households try to close the increasing income gap. Again, these findings are generally consistent with the earlier results on prosperity.
Results for car debt paint a similar picture, with households that are not liquidity or credit constrained and are willing to take financial risk borrowing much more for car purchases. That said, the evidence is somewhat weaker compared to investment debt.
| Investment | Car | |
|---|---|---|
| Panel A: Hand-to-mouth in t–4 | ||
| Hand-to-mouth | 1.29* (0.77) |
−0.05 (0.61) |
| Not hand-to-mouth | 3.84*** (1.30) |
0.65* (0.37) |
| No of observations | 7,631 | 7,631 |
| Panel B: Ability to raise emergency fund in t–4 | ||
| Cannot raise easily | 2.08*** (0.76) |
0.27 (0.52) |
| Can raise easily | 4.46*** (1.22) |
0.49 (0.46) |
| No of observations | 6,883 | 6,883 |
| Panel C: Financial attitude in t–4 | ||
| Not taking financial risk | 0.87 (0.71) |
−0.18 (1.24) |
| Taking financial risk | 13.91*** (5.35) |
1.78 (1.40) |
| No of observations | 4,645 | 4,645 |
| Household covariates | Y | Y |
| SA3 covariates | Y | Y |
| Group × SA3 interactions | Y | Y |
| SA3 time trends | Y | Y |
|
Notes: Clustered standard errors at SA3 level are in parentheses. ***, ** and * denote statistical significance at the 1, 5 and 10 per cent levels, respectively. Sources: ABS; Author's calculations; HILDA Survey Release 19.0 |
||
6. Robustness Checks
In this section, I perform several robustness checks. First, the sample of non-moving households are not necessarily random. For example, people might move to a low inequality neighbourhood with the aim to reduce their debts. I follow Atalay et al (2020) in controlling for this selection through a Heckman selection model. The selection equation takes the form:
I model the household decision not to move as a function of the lagged indicators of their intention to move, their satisfaction with their neighbourhood, and their satisfaction with their local community, while controlling for a range of factors similarly specified in Equation (1). The satisfaction measures are arguably exogenous. Estimates using the Heckman selection model are similar to those using the baseline model (Table B2) with the association between investment debt and local income inequality standing out as particularly significant, both statistically and economically.
Second, I employ the top 10 per cent share of total income as an alternative measure of local income inequality. This measure is more sensitive to changes that affect the upper tail of the distribution than the Gini coefficient, and to the extent that households compare themselves against their most affluent neighbours, could be more suitable for my analysis. Table B4 shows that the choice of inequality indicator does not influence the qualitative results. A 1 percentage point increase in the top 10 per cent share of local income is associated with more than a 2 percentage point increase in investment debt and 0.3 percentage point increase in car debt, both as a proportion of income.
Next, I check the results across a number of other sub-samples for robustness. First I remove the self-employed. These households may be more responsive to macro shocks, and also tend to have more investment debt, and as such it is possible that they are driving some of the results. However, by restricting the sample to not self-employed households I find that investment debt accumulation following an increase in inequality remains the same (Table B6).
I also consider a sub-sample of households with no change in household structure to abstract from shocks that result in a change in household structure, which in turn affects debt-taking behaviour. Restricting the sample to households not going through structural changes between the wealth modules, roughly 80 per cent of the main sample, the results are, again, largely unchanged (Table B7).
Similarly, households could have changed occupations, as a result of local economic conditions that also affect local inequality, such as the industrial composition. This change could simultaneously affect their debt accumulation. However, restricting the sample to households whose heads did not change occupations between the wealth modules yields an even stronger link between local inequality and investment debt accumulation (Table B8).
Finally, I simplify the model specification by removing the interaction terms between SA3 macro shocks and local income inequality. Estimates are broadly unchanged, suggesting that the heterogeneous relationship between local income inequality and debt accumulation across household distributions is not confounded by other SA3 macro shocks (Table B10).
7. Conclusion
While the relationship between local income inequality and financial behaviour of households has received a lot of attention in recent years, empirical evidence at the household level is scarce and inconclusive. Exploiting the very rich longitudinal household data from the HILDA Surveys, combined with income inequality data at an SA3 level from the ABS, I estimate the effect of a change in local income inequality on Australian household debt accumulation across different types of debt and how the effect varies by household demographic and financial characteristics.
I find that households significantly increase their investment debt and, to a lesser degree, car debt, following an increase in local income inequality. Heterogeneity analyses reveal that the effect is strongest for middle-aged, middle-income mortgagors with financial capacity and a willingness to take financial risk. These results shed additional light on the mechanisms and macroeconomic implications of the relationship between local inequality and household borrowing. More specifically, the paper lends evidence to the ‘keeping up with the Joneses’ dynamics, both via closing the consumption gap (with car debt) and closing the income gap (with investment debt). However, since households who exhibit such behaviour are well resourced, there does not appear to be a macrofinancial stability concern associated with the effect of local inequality on household indebtedness in Australia.
The findings in this paper highlight a number of areas for future research. In particular, the finding that households appear to try to close the income gap by borrowing more for investment leads to a natural question: Do households also try to ‘keep up with the Joneses’ through other channels? For example, could there be a link between local income inequality and labour supply decisions, such as secondary earners increasing their labour force participation? Or could individuals look to close the income gap by investing in their human capital to raise their earning potential? These questions are left to future research.
Appendix A: Summary Statistics
| Household variable | 2010 | 2014 | 2018 |
|---|---|---|---|
| Age (years) | 48.8 | 49.9 | 50.5 |
| Male (%) | 59.1 | 58.6 | 57.5 |
| Married (%) | 60.2 | 59.9 | 59.0 |
| Number of children (if having children) | 1.8 | 1.8 | 1.8 |
| University graduate (%) | 32.9 | 37.9 | 40.1 |
| Labour force (%) | 69.8 | 68.8 | 67.2 |
| Employed (%) | 67.5 | 66.5 | 64.9 |
| Home owner (%) | 66.6 | 64.4 | 64.4 |
| Gross income ($'000) | 89.3 | 91.7 | 92.8 |
| Net worth ($'000) | 789.9 | 776.8 | 919.0 |
| Financial wealth ($'000) | 294.4 | 330.2 | 380.9 |
| Total debt ($'000) | 181.4 | 182.7 | 200.3 |
| Mortgage debt ($'000) | 145.4 | 150.8 | 172.9 |
| Home debt ($'000) | 104.6 | 107.0 | 122.2 |
| Other property debt ($'000) | 40.7 | 43.8 | 50.7 |
| Non-mortgage debt ($'000) | 36.0 | 31.9 | 27.4 |
| Credit card debt ($'000) | 2.3 | 1.7 | 1.5 |
| Hire purchase debt ($'000) | 0.3 | 0.2 | 0.2 |
| Car debt ($'000) | 1.8 | 2.1 | 2.1 |
| Business debt ($'000) | 10.6 | 8.6 | 7.3 |
| Investment debt ($'000) | 6.8 | 5.5 | 3.5 |
| No of observations | 7,235 | 9,365 | 9,446 |
|
Sources: Author's calculations; HILDA Survey Release 19.0 |
|||
| Household variables | Mean | Standard deviation | No of observations |
|---|---|---|---|
| Age (years) | 48 | 16 | 2,115 |
| Male (%) | 60 | 50 | 2,115 |
| Married (%) | 60 | 50 | 2,062 |
| Number of children | 1 | 1 | 2,063 |
| University graduate (%) | 40 | 50 | 2,115 |
| Labour force (%) | 70 | 50 | 2,063 |
| Employed (%) | 70 | 50 | 2,063 |
| Home owner (%) | 70 | 50 | 2,112 |
| Gross income ($'000) | 95 | 72 | 2,115 |
| Income ranking | 3 | 1 | 2,115 |
| Hand-to-mouth (%) | 20 | 40 | 2,115 |
| Investment debt ($'000) | 7 | 47 | 2,115 |
|
Sources: Author's calculations; HILDA Survey Release 19.0 |
|||
Appendix B: Robustness Checks
| Total | Mortgage | Non-mortgage | |||
|---|---|---|---|---|---|
| Total | Home | Other property | |||
| Gini coefficient | 0.00 (0.01) |
−0.00 (0.00) |
0.00 (0.00) |
−0.01** (0.00) |
0.00 (0.01) |
| No of observations | 7,646 | 7,646 | 7,646 | 7,646 | 7,646 |
| Non-mortgage | |||||
| Credit card | Hire purchase | Car | Business | Investment | |
| Gini coefficient | −0.01 (0.01) |
0.00 (0.00) |
0.01*** (0.00) |
0.00 (0.00) |
0.00 (0.00) |
| No of observations | 7,646 | 7,646 | 7,646 | 7,646 | 7,646 |
| Household covariates | Y | Y | Y | Y | Y |
| SA3 covariates | Y | Y | Y | Y | Y |
| SA3 time trends | Y | Y | Y | Y | Y |
|
Notes: Clustered standard errors at SA3 level are in parentheses. ***, ** and * denote statistical significance at the 1, 5 and 10 per cent levels, respectively. Sources: ABS; Author's calculations; HILDA Survey Release 19.0 |
|||||
| Total | Mortgage | Non-mortgage | |||
|---|---|---|---|---|---|
| Total | Home | Other property | |||
| Gini coefficient | −5.35 (15.21) |
−8.70 (6.19) |
−4.24 (5.82) |
−4.47 (3.88) |
3.35 (14.00) |
| No of observations | 18,010 | 18,010 | 18,010 | 18,010 | 18,010 |
| Non-mortgage | |||||
| Credit card | Hire purchase | Car | Business | Investment | |
| Gini coefficient | −2.03 (13.09) |
−0.01 (0.13) |
0.50 (1.32) |
1.15 (4.53) |
3.32*** (0.88) |
| No of observations | 18,010 | 18,010 | 18,010 | 18,010 | 18,010 |
| Household covariates | Y | Y | Y | Y | Y |
| SA3 covariates | Y | Y | Y | Y | Y |
| SA3 time trends | Y | Y | Y | Y | Y |
|
Notes: Clustered standard errors at SA3 level are in parentheses. ***, ** and * denote statistical significance at the 1, 5 and 10 per cent levels, respectively. Sources: ABS; Author's calculations; HILDA Survey Release 19.0 |
|||||
| Variables in t–4 | Coefficient | Standard errors |
|---|---|---|
| Intention to move | −0.62 | 0.03 |
| Satisfaction with neighbourhood | 0.01 | 0.03 |
| Satisfaction with community | 0.14 | 0.03 |
| Age | 0.00 | 0.00 |
| Age squared | 0.00 | 0.00 |
| Male | −0.03 | 0.02 |
| Married | −0.19 | 0.04 |
| Number of children | 0.04 | 0.02 |
| Number of adults | 0.20 | 0.02 |
| University degree | −0.21 | 0.03 |
| Employed | 0.21 | 0.10 |
| Not in the labour force | 0.01 | 0.10 |
| Self-employed | 0.02 | 0.05 |
| Gross income | 0.00 | 0.00 |
| Assets | 0.00 | 0.00 |
| Financial assets | 0.00 | 0.00 |
| Liquid net worth | 0.00 | 0.00 |
| No of observations | 18,010 | |
| Lambda | 53.01 | 73.01 |
| Rho | 0.06 | |
| Sigma | 874.82 | |
|
Sources: ABS; Author's calculations; HILDA Survey Release 19.0 |
||
| Total | Mortgage | Non-mortgage | |||
|---|---|---|---|---|---|
| Total | Home | Other property | |||
| Gini coefficient | 3.02 (2.03) |
−0.96 (1.52) |
−1.36 (2.00) |
0.38 (1.74) |
2.59*** (0.78) |
| No of observations | 7,631 | 7,631 | 7,631 | 7,631 | 7,631 |
| Non-mortgage | |||||
| Credit card | Hire purchase | Car | Business | Investment | |
| Gini coefficient | −0.11 (0.09) |
0.00 (0.05) |
0.33** (0.16) |
0.02 (0.43) |
2.22*** (0.31) |
| No of observations | 7,631 | 7,631 | 7,631 | 7,631 | 7,631 |
| Household covariates | Y | Y | Y | Y | Y |
| SA3 covariates | Y | Y | Y | Y | Y |
| SA3 time trends | Y | Y | Y | Y | Y |
|
Notes: Clustered standard errors at SA3 level are in parentheses. ***, ** and * denote statistical significance at the 1, 5 and 10 per cent levels, respectively. Sources: ABS; Author's calculations; HILDA Survey Release 19.0 |
|||||
| Total | Mortgage | Non-mortgage | |||
|---|---|---|---|---|---|
| Total | Home | Other property | |||
| Gini coefficient | −1.26 (3.78) |
−6.05* (3.49) |
−2.86 (1.99) |
−3.19 (3.81) |
4.79*** (1.78) |
| No of observations | 7,646 | 7,646 | 7,646 | 7,646 | 7,646 |
| Non-mortgage | |||||
| Credit card | Hire purchase | Car | Business | Investment | |
| Gini coefficient | −0.25*** (0.09) |
0.03 (0.13) |
0.44*** (0.14) |
0.30 (1.43) |
3.87*** (1.31) |
| No of observations | 7,646 | 7,646 | 7,646 | 7,646 | 7,646 |
| Household covariates | Y | Y | Y | Y | Y |
| SA3 covariates | Y | Y | Y | Y | Y |
| SA3 time trends | Y | Y | Y | Y | Y |
|
Notes: Clustered standard errors at SA3 level are in parentheses. ***, ** and * denote statistical significance at the 1, 5 and 10 per cent levels, respectively. Sources: ABS; Author's calculations; HILDA Survey Release 19.0 |
|||||
| Total | Mortgage | Non-mortgage | |||
|---|---|---|---|---|---|
| Total | Home | Other property | |||
| Gini coefficient | 7.13* (4.03) |
−0.60 (2.78) |
−1.19 (2.81) |
0.53 (2.28) |
5.75*** (2.13) |
| No of observations | 6,794 | 6,794 | 6,794 | 6,794 | 6,794 |
| Non-mortgage | |||||
| Credit card | Hire purchase | Car | Business | Investment | |
| Gini coefficient | −0.14* (0.08) |
0.05 (0.05) |
0.18 (0.31) |
−0.13 (0.51) |
3.93*** (1.33) |
| No of observations | 6,794 | 6,794 | 6,794 | 6,794 | 6,794 |
| Household covariates | Y | Y | Y | Y | Y |
| SA3 covariates | Y | Y | Y | Y | Y |
| SA3 time trends | Y | Y | Y | Y | Y |
|
Notes: Clustered standard errors at SA3 level are in parentheses. ***, ** and * denote statistical significance at the 1, 5 and 10 per cent levels, respectively. Sources: ABS; Author's calculations; HILDA Survey Release 19.0 |
|||||
| Total | Mortgage | Non-mortgage | |||
|---|---|---|---|---|---|
| Total | Home | Other property | |||
| Gini coefficient | 5.29 (5.10) |
−4.71 (4.18) |
−5.68 (4.22) |
0.97 (4.16) |
5.49*** (1.50) |
| No of observations | 6,764 | 6,764 | 6,764 | 6,764 | 6,764 |
| Non-mortgage | |||||
| Credit card | Hire purchase | Car | Business | Investment | |
| Gini coefficient | −0.22 (0.22) |
0.02 (0.10) |
0.50** (0.22) |
0.71 (1.15) |
3.84*** (1.12) |
| No of observations | 6,764 | 6,764 | 6,764 | 6,764 | 6,764 |
| Household covariates | Y | Y | Y | Y | Y |
| SA3 covariates | Y | Y | Y | Y | Y |
| SA3 time trends | Y | Y | Y | Y | Y |
|
Notes: Clustered standard errors at SA3 level are in parentheses. ***, ** and * denote statistical significance at the 1, 5 and 10 per cent levels, respectively. Sources: ABS; Author's calculations; HILDA Survey Release 19.0 |
|||||
| Total | Mortgage | Non-mortgage | |||
|---|---|---|---|---|---|
| Total | Home | Other property | |||
| Gini coefficient | 17.57*** (6.72) |
0.35 (5.12) |
−2.60 (5.87) |
2.95 (2.63) |
13.07** (5.44) |
| No of observations | 4,737 | 4,737 | 4,737 | 4,737 | 4,737 |
| Non-mortgage | |||||
| Credit card | Hire purchase | Car | Business | Investment | |
| Gini coefficient | −0.11 (0.11) |
−0.02 (0.07) |
0.28 (0.38) |
0.32 (3.13) |
6.06** (3.04) |
| No of observations | 4,737 | 4,737 | 4,737 | 4,737 | 4,737 |
| Household covariates | Y | Y | Y | Y | Y |
| SA3 covariates | Y | Y | Y | Y | Y |
| SA3 time trends | Y | Y | Y | Y | Y |
|
Notes: Clustered standard errors at SA3 level are in parentheses. ***, ** and * denote statistical significance at the 1, 5 and 10 per cent levels, respectively. Sources: ABS; Author's calculations; HILDA Survey Release 19.0 |
|||||
| Investment | Car | |
|---|---|---|
| 1st quartile | 0.40 (0.74) |
0.11 (1.91) |
| 2nd quartile | 1.74** (0.84) |
0.20 (0.44) |
| 3rd quartile | 8.79** (5.46) |
1.14*** (0.39) |
| 4th quartile | 3.38 (2.99) |
0.28 (0.21) |
| No of observations | 7,568 | 7,568 |
| Household covariates | Y | Y |
| SA3 covariates | Y | Y |
| Group × SA3 interactions | Y | Y |
| SA3 time trends | Y | Y |
|
Notes: Clustered standard errors at SA3 level are in parentheses. ***, ** and * denote statistical significance at the 1, 5 and 10 per cent levels, respectively. Sources: ABS; Author's calculations; HILDA Survey Release 19.0 |
||
| Investment | Car | Investment | Car | ||
|---|---|---|---|---|---|
| Local income ranking | Self-perceived prosperity | ||||
| 1st quartile | 0.84 (0.88) |
0.44 (1.77) |
Very poor | 1.33 (2.02) |
1.87 (2.05) |
| 2nd quartile | 1.43*** (0.50) |
−0.12 (0.23) |
Poor | 1.75*** (0.58) |
0.07 (0.74) |
| 3rd quartile | 11.00** (4.89) |
0.96*** (0.36) |
Just getting along | 1.80*** (0.65) |
−1.29 (1.37) |
| 4th quartile | −0.24 (1.46) |
0.76** (0.33) |
Reasonably comfortable | 6.49** (2.84) |
1.06 (0.74) |
| Very comfortable | 1.77 (1.50) |
1.01*** (0.37) |
|||
| Prosperous | −0.05 (3.48) |
2.87*** (0.58) |
|||
| No of observations | 7,568 | 7,568 | No of observations | 6,952 | 6,952 |
| Life cycle | Housing tenure | ||||
| 20 ≤ Agei,t–4 ≤ 39 | 2.32*** (0.66) |
−0.69 (0.82) |
Renters | 0.86 (0.65) |
−0.30 (1.01) |
| 40 ≤ Agei,t–4 ≤ 64 | 4.79** (2.09) |
1.25*** (0.43) |
Mortgagors | 9.01*** (3.16) |
0.75 (0.76) |
| Agei,t–4 ≥ 65 | 0.75 (0.93) |
0.29 (0.31) |
Outright home owners | 1.84 (2.74) |
1.23* (0.72) |
| No of observations | 7,395 | 7,395 | No of observations | 5,958 | 5,958 |
| Hand-to-mouth | Ability to raise emergency fund | ||||
| Hand-to-mouth | 1.41* (0.77) |
−0.50 (0.35) |
Cannot raise easily | 1.77* (0.97) |
−0.11 (0.26) |
| Not hand-to-mouth | 3.79*** (1.33) |
0.75** (0.33) |
Can raise easily | 4.54*** (1.21) |
0.62 (0.39) |
| No of observations | 7,631 | 7,631 | No of observations | 6,883 | 6,883 |
| Financial attitude | |||||
| Not taking financial risk | 1.41 (0.88) |
0.21 (0.83) |
|||
| Taking financial risk | 12.81** (5.47) |
1.56 (1.23) |
|||
| No of observations | 4,645 | 4,645 | |||
| Household covariates | Y | Y | Household covariates | Y | Y |
| SA3 covariates and time trends | Y | Y | SA3 covariates and time trends | Y | Y |
| Group × SA3 interactions | N | N | Group × SA3 interactions | N | N |
|
Notes: Clustered standard errors at SA3 level are in parentheses. ***, ** and * denote statistical significance at the 1, 5 and 10 per cent levels, respectively. Sources: ABS; Author's calculations; HILDA Survey Release 19.0 |
|||||
| Home | Other property | Home | Other property | ||
|---|---|---|---|---|---|
| Local income ranking | Self-perceived prosperity | ||||
| 1st quartile | 4.31 (17.73) |
−29.15 (24.19) |
Very poor | −36.06 (24.63) |
71.70* (39.67) |
| 2nd quartile | −6.46 (6.33) |
2.68 (4.40) |
Poor | −6.65 (13.69) |
0.81 (5.29) |
| 3rd quartile | −6.05 (6.30) |
4.92 (7.12) |
Just getting along | 6.13 (7.30) |
4.09 (5.20) |
| 4th quartile | −7.34 (5.55) |
−0.06 (5.46) |
Reasonably comfortable | −1.74 (8.36) |
−6.45 (15.22) |
| Very comfortable | −8.09* (4.54) |
−6.23 (4.98) |
|||
| Prosperous | −19.74 (17.67) |
15.94 (18.38) |
|||
| No of observations | 7,568 | 7,568 | No of observations | 6,952 | 6,952 |
| Life cycle | Housing tenure | ||||
| 20 ≤ Agei,t–4 ≤ 39 | 3.09 (4.43) |
−1.61 (8.80) |
Renters | −0.61 (2.77) |
−53.03 (54.60) |
| 40 ≤ Agei,t–4 ≤ 64 | −1.28 (5.48) |
−17.34 (30.12) |
Mortgagors | 0.51 (8.54) |
4.57 (9.09) |
| Agei,t–4 ≥ 65 | −9.12 (10.59) |
12.31 (25.93) |
Outright home owners | −1.47 (4.77) |
2.94 (12.41) |
| No of observations | 7,395 | 3,158 | No of observations | 5,958 | 2,972 |
| Hand-to-mouth | Ability to raise emergency fund | ||||
| Hand-to-mouth | −0.98 (6.15) |
41.17* (23.74) |
Cannot raise easily | 1.07 (4.68) |
−2.75 (14.11) |
| Not hand-to-mouth | −4.98 (4.79) |
−7.02 (19.13) |
Can raise easily | −3.01 (5.07) |
−6.06 (23.12) |
| No of observations | 7,631 | 3,209 | No of observations | 6,883 | 2,955 |
| Financial attitude | |||||
| Not taking financial risk | −0.44 (6.51) |
0.99 (11.77) |
|||
| Taking financial risk | −1.59 (11.57) |
−24.19 (88.29) |
|||
| No of observations | 4,645 | 1,883 | |||
| Household covariates | Y | Y | Household covariates | Y | Y |
| SA3 covariates and time trends | Y | Y | SA3 covariates and time trends | Y | Y |
| Group × SA3 interactions | N | N | Group × SA3 interactions | N | N |
|
Notes: Clustered standard errors at SA3 level are in parentheses. ***, ** and * denote statistical significance at the 1, 5 and 10 per cent levels, respectively. Sources: ABS; Author's calculations; HILDA Survey Release 19.0 |
|||||
References
ABS (Australian Bureau of Statistics) (2022), ‘Survey of Income and Housing, User Guide, Australia’, 2019-20 financial year, accessed May 2022. Available at <https://www.abs.gov.au/statistics/detailed-methodology-information/concepts-sources-methods/survey-income-and-housing-user-guide-australia/2019-20>.
Aguiar MA, M Bils and C Boar (2020), ‘Who Are the Hand-to-Mouth?’, NBER Working Paper 26643.
Atalay K, GF Barrett, R Edwards and C Yu, (2020), ‘House Price Shocks, Credit Constraints and Household Indebtedness’, Oxford Economic Papers, 72(3), pp 780–203.
Berlemann M and J Salland (2016), ‘The Joneses' Income and Debt Market Participation: Empirical Evidence from Bank Account Data’, Economics Letters, 142, pp 6–9.
Browning M, M Gørtz and S Leth-Petersen (2013), ‘Housing Wealth and Consumption: A Micro Panel Study’, The Economic Journal, 123(568), pp 401–428.
Coibion O, Y Gorodnichenko, M Kudlyak and J Mondragon (2020), ‘Greater Inequality and Household Borrowing: New Evidence from Household Data’, Journal of the European Economic Association, 18(6), pp 2922–2971.
Cox D and T Jappelli (1993), ‘The Effect of Borrowing Constraints on Consumer Liabilities’, Journal of Money, Credit and Banking, 25(2), pp 197–213.
Dobson C and K Hooper (2015), ‘Insights from the Australian Tourism Industry’, RBA Bulletin, March, pp 21–31.
Duca JV and SS Rosenthal (1993), ‘Borrowing Constraints, Household Debt, and Racial Discrimination in Loan Markets’, Journal of Financial Intermediation, 3(1), pp 77–103.
Gastwirth JL (2017), ‘Is the Gini Index of Inequality Overly Sensitive to Changes in the Middle of the Income Distribution?’, Statistics and Public Policy, 4(1), pp 1–11.
Georgarakos D, M Haliassos and G Pasini (2014), ‘Household Debt and Social Interactions’, The Review of Financial Studies, 27(5), pp 1404–1433.
Guerrieri V, D Hartley and E Hurst (2013), ‘Endogenous Gentrification and Housing Price Dynamics’, Journal of Public Economics, 100, pp 45–60.
Johnson KW and G Li (2010), ‘The Debt-Payment-to-Income Ratio as an Indicator of Borrowing Constraints: Evidence from Two Household Surveys’, Journal of Money, Credit and Banking, 42(7), pp 1373–1390.
Kaplan G, GL Violante and J Weidner (2014), ‘The Wealthy Hand-to-Mouth’, Brookings Papers on Economic Activity, Spring, pp 77–138.
Khandaker S and SZ Islam (2017), ‘International Tourism Demand and Macroeconomic Factors’, International Journal of Economics and Financial Issues, 7(5), pp 389–393.
Kreiner CT, DD Lassen, and S Leth-Petersen (2019), ‘Liquidity Constraint Tightness and Consumer Responses to Fiscal Stimulus Policy’, American Economic Journal: Economic Policy, 11(1), pp 351–379.
Loschiavo D (2021), ‘Household Debt and Income Inequality: Evidence from Italian Survey Data’, The Review of Income and Wealth, 67(1), pp 61–103.
Price F, B Beckers and G La Cava (2019), ‘The Effect of Mortgage Debt on Consumer Spending: Evidence from Household-Level Data’, RBA Research Discussion Paper No 2019-06.
Productivity Commission (2019), ‘Is Australia Becoming More Unequal?’, PC News, 65, pp 6–13.
Stiglitz JE (2012), ‘Macroeconomic Fluctuations, Inequality, and Human Development’, Journal of Human Development and Capabilities, 13(1), pp 31–58.
Copyright and Disclaimer Notices
HILDA Survey Disclaimer Notice
This paper uses unit record data from the Household, Income and Labour Dynamics in Australia (HILDA) Survey. The unit record data from the HILDA Survey was obtained from the Australian Data Archive, which is hosted by The Australian National University. The HILDA Survey was initiated and is funded by the Australian Government Department of Social Services (DSS) and is managed by the Melbourne Institute of Applied Economic and Social Research (Melbourne Institute). The findings and views based on the data, however, are those of the authors and should not be attributed to the Australian Government, DSS, the Melbourne Institute, the Australian Data Archive or The Australian National University and none of those entities bear any responsibility for the analysis or interpretation of the unit record data from the HILDA Survey provided by the authors.
RP Data Pty Ltd Trading as CoreLogic Asia Pacific Disclaimer Notice
This publication contains data, analytics, statistics, results and other information licensed to the Reserve Bank of Australia by RP Data Pty Ltd trading as CoreLogic Asia Pacific (CoreLogic Data).
© Copyright 2022. RP Data Pty Ltd trading as CoreLogic Asia Pacific (CoreLogic) and its licensors are the sole and exclusive owners of all rights, title and interest (including intellectual property rights) subsisting in the CoreLogic Data reproduced in this publication. All rights reserved.
The CoreLogic Data provided in this publication is of a general nature and should not be construed as specific advice or relied upon in lieu of appropriate professional advice.
While CoreLogic uses commercially reasonable efforts to ensure the CoreLogic Data is current, CoreLogic does not warrant the accuracy, currency or completeness of the CoreLogic Data and to the full extent permitted by law excludes all loss or damage howsoever arising (including through negligence) in connection with the CoreLogic Data.
Acknowledgements
I would like to thank Nalini Agarwal, Kadir Atalay, Benjamin Beckers, James Bishop, Anthony Brassil, Deborah Cobb-Clark, Thomas Cusbert, Jonathan Hambur, Patrick Hendy, Gianni La Cava, Gulnara Nolan, Gabrielle Penrose, Matthew Read, John Simon, Brian Tran, Michelle Wright and Anirudh Yadav for their feedback. The views expressed in this paper are those of the author and do not necessarily reflect the views of the Reserve Bank of Australia. The author is solely responsible for any errors.
Footnotes
The Gini coefficient is defined as the ratio of the area between the actual Lorenz curve and the diagonal (or line of equality) and the total area under the diagonal. The Gini coefficient ranges between zero when all incomes are equal and one when one unit receives all the income, that is, the smaller the Gini coefficient the more even the distribution of income (ABS 2022). [1]
SA3s are designed to provide a regional breakdown of Australia and often closely align to Local Government Areas. There are 358 SA3 areas in Australia, with a population of between 30,000 and 130,000 people (ABS 2022). [2]
First, I determine household heads in the first year, and assign the household head ID and a unique household ID to all members of the household. The household head is identified following the standard tiebreaking procedure. For each following year, I identify household splits and mergers, and the source of change. I then move household IDs forward for as many households as possible, dependent on the identified change above. For more details on the procedures, see Price et al (2019). [3]
See the ABS release ‘Household Income and Wealth, Australia’ for the 2017-18 financial year. [4]
The heterogeneous interactions between individual household-level characteristics are unlikely to confound the heterogeneous effects of SA3-level inequality. [5]
SD of changes within SA3s over time, equivalent to around 0.02 index points. [6]
Results for debt accumulation in monetary terms are robust and can be found in Table B5. [7]
I examine the extensive margin by estimating the probability of holding debt across different types of debt. Results in Table B1 suggest that the extensive margin does not matter and debt accumulation is driven by the intensive margin. [8]
Question asked in the HILDA Survey: ‘Given your current needs and financial responsibilities, would you say that you and your family are …’ with six possible answers, including ‘prosperous’, ‘very comfortable’, ‘reasonably comfortable’, ‘just getting along’, ‘poor’, and ‘very poor’. [9]
Question in the HILDA Survey: ‘Suppose you had only one week to raise $2000 for an emergency. Which of the following best describes how hard it would be for you to get that money?’ Answers are grouped into ‘can raise easily’ if respondents answered ‘Could easily raise emergency funds’ and ‘cannot raise easily’ for the rest. [10]
Question in the HILDA Survey: ‘Which of the following statements comes closest to describing the amount of financial risk that you are willing to take with your spare cash? That is, cash used for savings or investment.’ Answers are grouped into ‘willing to take risk’ if respondents answered ‘average’ and above and ‘not willing to take risk’ for the rest. [11]