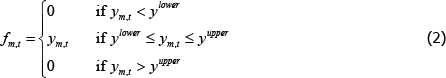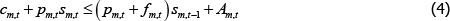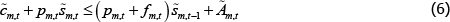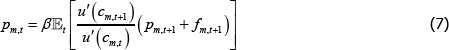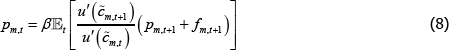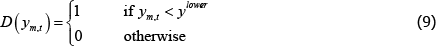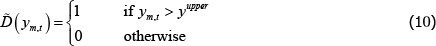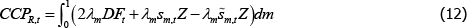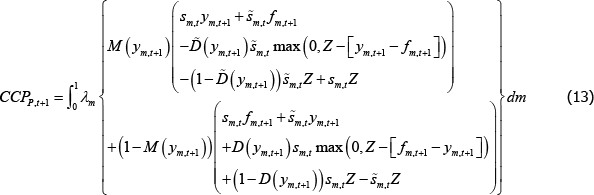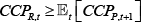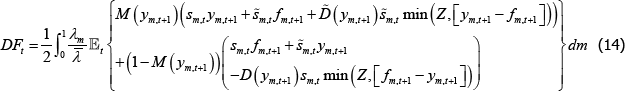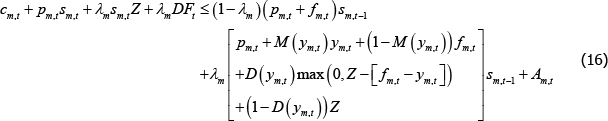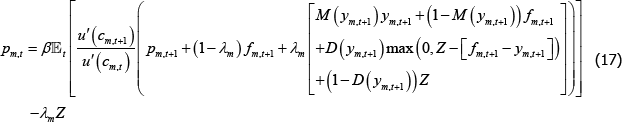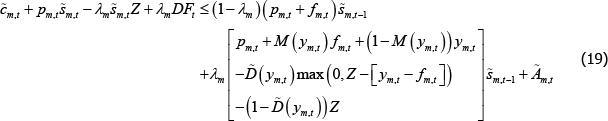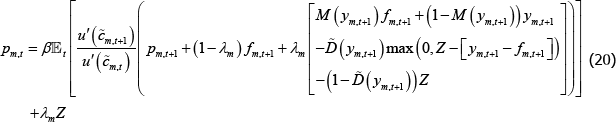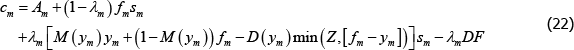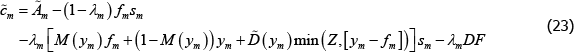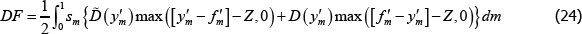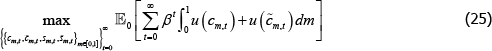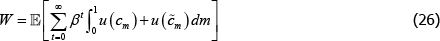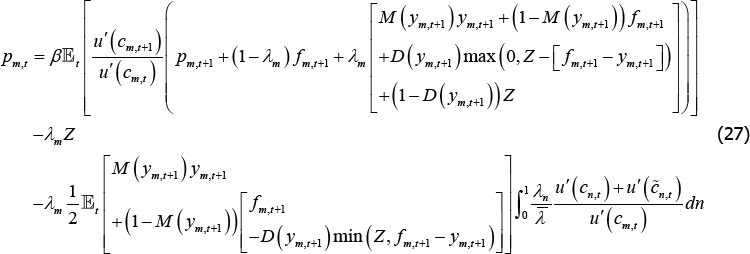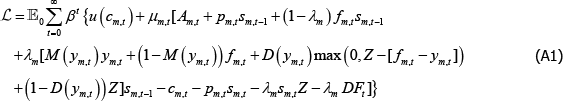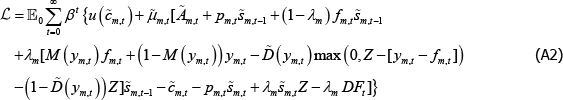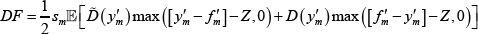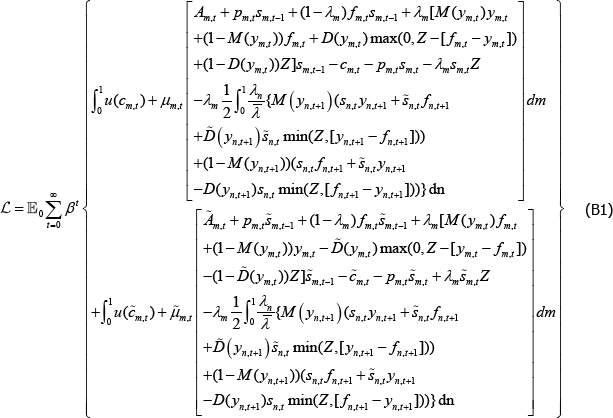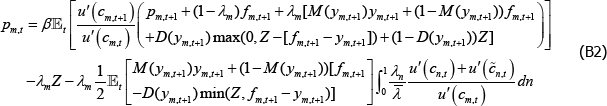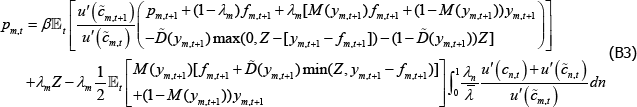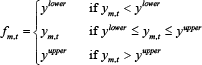Research Discussion Paper – RDP 2016-07 The Efficiency of Central Clearing: A Segmented Markets Approach
1. Introduction
Following the global financial crisis, the G20 agreed on a number of reforms to financial markets. Member nations agreed to improve market transparency, reduce interconnectedness between market participants, and improve the management and collateralisation of bilateral credit risk. To this end, a key area of the reform agenda has been to mandate the use of central counterparties (CCPs) for certain over-the-counter (OTC) derivatives.
In line with these agreed reforms, Australian financial regulators have implemented mandatory central clearing requirements for certain interest rate derivatives (APRA, ASIC and RBA 2015; ASIC 2015; Australian Treasury 2015). A number of other jurisdictions – including the European Union, Japan and the United States – have implemented similar requirements.[1]
This paper studies how mandatory central clearing affects market participants' incentives in OTC derivatives markets. The questions that we address are: How does a regulatory requirement for central clearing affect trade in derivatives? Under what conditions does a CCP improve welfare when managing counterparty credit risk? What does the optimal structure for mandatory central clearing look like?
To address these questions we use a micro-founded general equilibrium model with segmented and incomplete markets. The main advantage of this approach is that traders, allocations and prices endogenously respond to different central clearing arrangements; these responses can be material for the efficiency of any reform proposed. It also facilitates quantitative statements about the welfare implications of alternative market reforms. The existing literature has typically not considered endogenous allocations and prices or permitted quantitative welfare analysis. The disadvantage of our approach is that we cannot consider all market frictions relevant to the question of optimal central clearing, such as the role of size and networks in contractual relationships (Allen and Gale 2000; Jackson and Manning 2007; Duffie and Zhu 2011; Heath, Kelly and Manning 2013), or market opacity (Acharya and Bisin 2014).
The model is motivated by the market segmentation model of Edmond and Weill (2012). Traders face idiosyncratic risks that they can hedge by buying or selling OTC derivatives from other traders in their market. These contracts reference an underlying financial price and are zero sum.
There are two key market frictions. The first is that traders can only exchange contracts in the market in which they trade. Second, traders are exposed to the risk of counterparty default, which cannot be privately insured against. This environment creates a role for CCPs to provide default insurance. The CCP in our model does so by guaranteeing payment on all contracts that it clears. It covers its obligations by collecting two types of resources: per-contract initial margin requirements – resources that the CCP collects from traders in advance and uses if the trader defaults; and a default fund contribution that can be used to cover any losses remaining once defaulting traders' initial margin has been exhausted. We do not consider variation margin – cash exchanged daily in response to mark-to-market changes in participants' OTC derivatives portfolios – as the model is calibrated to match quarterly data (the coupon frequency of the majority of OTC derivatives).
Using this framework, we find that mandatory central clearing:
- can be welfare improving because it mutualises counterparty credit risk
- increases welfare if initial margin requirements are set optimally, but can be inefficient otherwise
- is more beneficial the higher the probability of default and the more effective are OTC derivative contracts as a hedge against idiosyncratic risk.
Our findings capture the trade-off between the default insurance that a CCP provides and the incentive for market participants to trade ‘too much’ when default losses are mutualised through the CCP's default fund. This is akin to a moral hazard problem in insurance where an agent undertakes too much of a risky activity when insurance is provided.
Default insurance is beneficial in our model because it reduces traders' consumption variance. Since, in the model, traders do not have access to private insurance against the risk of counterparty default, the core benefit of a CCP is that it provides insurance that would not otherwise exist.[2] This default insurance function is a material benefit of central clearing that, to date, the literature has not explored in a general equilibrium framework.
The main cost of central clearing that we consider is that it alters market participants' incentives. With default insurance, traders have the incentive to write more financial contracts than they otherwise would. Because the cost of insurance provided by the CCP is mutualised among all CCP participants, it is not internalised at the individual level. This generates a ‘mutualisation externality’, which means that privately optimal trade does not coincide with socially optimal trade.
In terms of related literature, the role of CCPs as insurance providers and how CCPs affect trader decision-making have not been widely studied. However, our paper connects to an emerging research field on optimal CCP design including: Acharya and Bisin (2014) who study an externality in financial trade due to opacity in counterparty positions; Duffie and Zhu (2011) who study the role of a network and contract netting; Heath, Kelly and Manning (2015) who study the transmission of financial stress through a network; Heath et al (forthcoming) who use portfolio-level data from 41 large OTC derivatives market participants to inform analysis of the stability of the financial network and how losses might be transmitted in times of stress; and Koeppl, Monnet and Temzelides (2012) who study cross-subsidisation between centralised and non-centralised markets. Our paper is also related to Pirrong (2009), who discusses the importance of the moral hazard problems that central clearing can engender, and Haene and Sturm (2009) who use a stylised model to analyse the extent to which CCPs should rely on initial margin versus their default fund. The modelling approach we use draws from Edmond and Weill (2012).
The paper is structured as follows: Section 2 provides background on OTC derivatives markets and CCPs, and a brief overview of the existing literature. Section 3 outlines our model. Section 4 presents our results, including: the welfare benefits of OTC derivatives; the effect of central clearing on trade and welfare, and how appropriately set margin requirements are important in ensuring the welfare benefits of central clearing are realised. We then turn to the question of the optimal level of mandatory clearing and discuss some policy implications of our results. Section 5 concludes.
2. Background
2.1 OTC Derivatives
OTC derivatives are a type of financial contract that are traded bilaterally, rather than on a central exchange.[3] They are contracts that specify a payment (or stream of payments) based on the value of an underlying reference price at a specified date (or dates). Examples of the prices against which OTC derivatives contracts are written include interest rates, credit spreads, commodity prices, equity prices and exchange rates. These contracts are typically used to hedge risks. For instance: resource companies might use them to manage price risks associated with the commodities they produce; non-financial corporations might hedge the interest rate risk on a bond issue; investment funds might hedge the foreign exchange risk of overseas investments; and banks might hedge the credit of a large syndicated loan. The OTC derivatives market is large and is dominated by contracts that reference interest rates (Figure 1). Much of the volume in the market is trades between banks and other large financial firms that are managing risks arising from other transactions. These risks might arise, for instance, from client-facing OTC derivatives transactions, such as with a non-financial corporation.
Because OTC derivatives are traded bilaterally, market participants face ‘counterparty credit risk’ – the risk that their counterparty will fail to honour some or all of its obligations. Although not limited to OTC derivatives, this risk is particularly hard to diversify in these markets because participants tend to have few counterparty relationships across which they can diversify their counterparty risk, relative to the size of their OTC derivatives positions. There are two reasons for this. First, the market is quite concentrated, and for certain product areas there may be only a limited number of available counterparties. Second, before participants can enter into OTC derivatives contracts, they must negotiate extensive documentation. Establishing and negotiating these trading relationships is expensive and time-consuming, particularly for smaller market participants. Once negotiated, these ‘Master Agreements’ cover all trades subsequently struck between counterparties. This means trading relationships for OTC derivatives are characterised by high fixed costs, but low marginal costs. Further, although private insurance against counterparty credit risk exists in the real world through CDS, these are available only for fairly large institutions. Moreover, the protection buyer is still exposed to the credit risk of the counterparty on the CDS.[4]
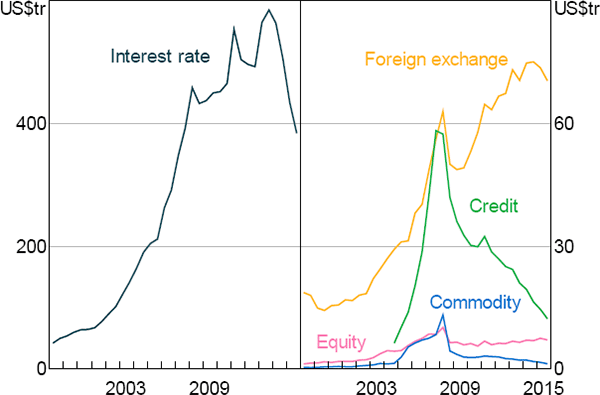
Source: BIS
2.2 Central Counterparties
A CCP is an entity that stands between counterparties to help alleviate counterparty credit risk. It does so through novation, where the CCP steps in after a contract is struck bilaterally and becomes the buyer to every seller and the seller to every buyer. In doing so, the original bilateral contract is torn up and the CCP assumes the counterparty credit risk. Although the counterparties are still exposed to the credit risk of the CCP, a CCP is designed to be a stronger credit than a bilateral counterparty.
CCPs ensure their high creditworthiness by using three types of financial resources to protect themselves from the default of their participants: initial margin, which is the collateral initially collected by a CCP and retained in the event of default (and so can be used to meet counterparty payments on the defaulting contract); variation margin, where cash is exchanged to reflect changes in the mark-to-market value of a participant's OTC derivatives portfolio; and a mutualised default fund, funded by all of the CCP's participants.[5]
Initial margin is the collateral that a CCP collects from participants to protect itself from a participant default. Under international standards, ‘initial margin should meet an established single-tailed confidence level of at least 99 percent with respect to the estimated distribution of future exposure’ (CPSS-IOSCO 2012, p 50).[6]
Variation margin is a payment that reflects mark-to-market changes in the value of participants' OTC derivatives. It is settled in cash, typically daily – although some CCPs settle intradaily. Because the CCP stands between participants (and does not enter transactions for its own account) the transaction is zero-sum for the CCP: variation margin received from participants with mark-to-market losses is passed to participants with mark-to-market gains.
CCPs also collect financial resources from all of their participants through a default fund. The default fund is used by the CCP if a defaulting participant's initial margin is not sufficient to meet the default losses. CCPs generally contribute some of their own capital to this pool, but the majority comes from participants. Under international standards, this pool must be sufficient to cover the simultaneous default of the CCP's two largest participants in extreme but plausible scenarios.[7] Participants must contribute to the default fund when they join a CCP. Thereafter, the default fund is resized (and contributions called for) relatively infrequently.
If the default fund is insufficient, the CCP can become insolvent. However, CCPs have additional procedures to prevent insolvency in this case, such as calling for additional resources from surviving participants. These steps are known as ‘recovery’ (for further detail, see Gibson (2013), CPMI-IOSCO (2014) and Heath et al (2015)).[8]
2.3 Literature
Questions surrounding CCPs and OTC derivatives markets have become an active area of research in recent years. Following work by Allen and Gale (2000) on networks and financial contagion, Jackson and Manning (2007) and Duffie and Zhu (2011) use network models to study how CCPs affect the distribution of risk in OTC derivative markets. A number of papers use a similar methodology, including Heller and Vause (2012), Anderson, Dion and Perez-Saiz (2013), and Heath et al (2013, 2015).
These papers focus on the network of links between participants in OTC derivatives markets and how central clearing can affect system-wide exposures and, indirectly, the collateral required by the system. This literature has taken the initial structure of the network as exogenous, and does not allow for optimising behaviour on the part of traders, or for market prices to be determined endogenously.
An alternative strand of literature has allowed for optimising behaviour on the part of traders with the use of general equilibrium finance models, which typically have a few periods. In these models, one core market failure is incomplete information. Acharya and Bisin (2014) show that opacity in OTC derivative markets can lead to a ‘counterparty risk externality’, overleveraging and socially inefficient default. A centralised clearing mechanism – such as a CCP – that is able to provide information on all participants' positions could resolve this market failure. Similar papers in this vein include Koeppl and Monnet (2008, 2010), who study limited commitment, and Biais, Heider and Hoerova (2012) who study costly monitoring.
Haene and Sturm (2009) is also related. They use a model of CCP risk management to analyse the trade-off between initial margin and the default fund. However, their model is static, and does not allow for: optimising behaviour on the part of traders; welfare analysis; or consideration of the optimal level of central clearing. These are the main contributions of our paper. Carter, Hancock and Manning (2015) also examine what factors influence CCPs' choice risk controls and the role that regulation plays. For a broader survey of the issues surrounding central clearing, including the importance of moral hazard (the focus of our paper), see Pirrong (2009).
3. The Model
We use a consumption-based asset pricing model with market segmentation, in the spirit of Edmond and Weill (2012), to study central clearing and OTC derivatives. Our core modifications are to: introduce default to provide a motive for counterparty insurance; model bilateral zero-sum financial trade explicitly; and include a modelling device for central clearing through a CCP.
In brief, our model has a continuum of markets for OTC derivatives, each of which contains two types of traders who can trade only in that market. Traders enter into OTC derivatives contracts to offset an idiosyncratic risk they face – that is, to hedge – but they can only do so imperfectly because markets are incomplete and the contract that traders have access to is not perfectly negatively correlated with their endowment risk. The pay-offs on a contract are symmetric around zero – traders are equally likely to owe money on a contract as they are to receive it. The OTC derivatives contract is the only way traders can manage endowment risk. This assumption is designed to capture the specific nature of financial risks that we have in mind when financial market participants engage in OTC market trade. It is different from other incomplete markets models, such as Bewley models, where traders can self-insure (for example, through savings) against endowment risk. The structure of our model is designed to be akin to the trades between banks and other large financial firms, but abstracts from the actual source of the risk – that is, we do not model the dealer-client structure explicitly.
Traders also face counterparty credit risk. That is, when extreme price movements occur one of the parties to the trade is assumed to default and no contract payment is made. In such a state, the marginal utility of the holder of the hedge (who is expecting, but not receiving, payment) is likely to be high, because of the low payout on the underlying asset they are trying to hedge. This makes default costly. The only way traders can mitigate counterparty credit risk in our model is to novate contracts with the CCP. We do not consider other ways of managing bilateral counterparty credit risk, such as bilateral margin or CDS. To the extent that these alternative mechanisms are used, they might reduce the value of insurance provided through a CCP. However, both bilateral margin and CDS provide only partial insurance and, thus, even in these cases it is likely that the insurance benefits from central clearing will exist.[9]
The advantages of using a consumption-based asset pricing model are threefold. First, it allows for optimising behaviour on the part of traders, so that traders can endogenously respond to changes in the regulation of OTC derivatives markets. This is an important benefit relative to much of the existing literature on OTC derivatives markets because market participants' behaviour is unlikely to remain constant in the face of such policy changes. Second, our approach allows quantitative statements to be made about the relative efficiency of alternative policies. In the existing literature, it is often the case that one policy can be ranked qualitatively relative to other policies, but quantitative statements such as the optimal level of margin or the optimal level of mandatory clearing are much more difficult to infer. Third, our model has an appealing theoretical interpretation in terms of sharing counterparty risks, which are a fundamental reason CCPs exist.
Of course, our approach has limitations as well. In particular, we must abstract from many of the important features of OTC derivatives that the existing literature has studied. For instance: we do not consider how networks affect the structure of risk and the efficiency of netting arrangements (e.g. Duffie and Zhu 2011; Heath et al 2015); the relationship between clients and dealers (Neklyudov and Sambalaibat 2015); or the role of market information and opacity (Acharya and Bisin 2014). These are important considerations for policymakers, but are beyond the scope of our paper.
The rest of this section sets out the model formally. We first introduce our traders and the model structure without the CCP to illustrate the underlying decision problem (Sections 3.1 to 3.4). We then introduce the CCP and show how that affects traders' maximisation problems (Section 3.5). Next, we characterise the equilibrium of our model, along with an alternative ‘constrained-efficient’ benchmark (Section 3.6). Section 3.7 details how we calibrate the model.
3.1 The Markets and Contracts
There is a continuum of markets on the unit interval, indexed by m. Each market could represent a particular product: one market might represent 10-year Australian dollar-denominated fixed-for-floating interest rate swaps; another, 1-year Japanese yen-denominated overnight index swaps; and another, 3-month Australian dollar-US dollar forwards.
There are two types of traders within each market – a ‘long trader’ and a ‘short trader’. We assume a unit mass of identical long traders and, separately, short traders within each market. This implies that each trader takes the price of the contract as given. Because all long traders within a market are identical and are price takers, we use a representative long trader (and likewise for short traders).
All long traders in market m receive a market-specific endowment Am,t. All short traders in the same market m receive Ãm,t. Endowments between the two types offset exactly, such that there is no aggregate risk in a market:
where εm,t is independently and identically distributed 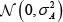 across markets.[10]
across markets.[10]
The OTC derivatives contract is an agreement to pay an amount determined by a market-specific
random variable ym,t, which is distributed 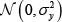 and
is negatively correlated with the stochastic component of the endowment payment,
corr(εm,t, ym,t) < 0.[11]
OTC derivatives contracts are infinitely lived, and pay out in period t + 1 based on
the volume held from period t.
and
is negatively correlated with the stochastic component of the endowment payment,
corr(εm,t, ym,t) < 0.[11]
OTC derivatives contracts are infinitely lived, and pay out in period t + 1 based on
the volume held from period t.
3.2 Default
We model counterparty credit risk by assuming that obligations on the contract are capped – that is, default is exogenous, not strategic, and depends only on the realised value of ym,t.[12] Specifically: if ym,t is negative and below a given threshold (requiring a large payment from the long trader to the short trader in market m), long traders will default and not pay what they owe to short traders. Similarly, if ym,t is sufficiently positive (i.e. above a given symmetric threshold), short traders will default on their obligations to long traders. The default thresholds are exogenous and, in the event of default, no payment is made.[13] Exogenous default is common in the literature on CCPs, although Acharya and Bisin (2014) is a notable exception.
Formally, the payments traders actually make to or receive from their counterparty are given by:[14]
This pay-off structure creates a pay-off distribution that would otherwise be normal, but where traders receive zero for any draw outside the default bounds. Figure 2 shows the density of ym,t and shades the regions where default events occur.
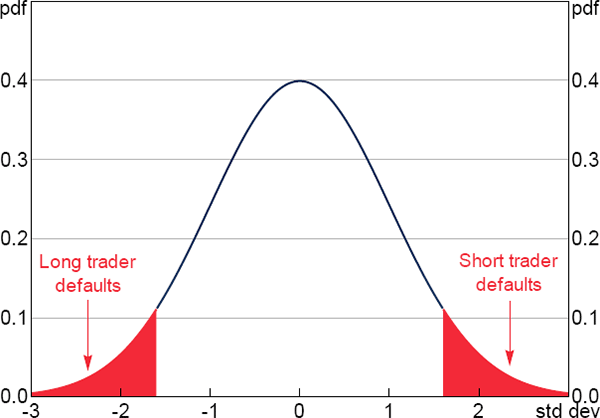
Although our representation of default is stylised, it has the advantage of being simple and highly tractable. These are important in a general equilibrium environment. We do not view our assumptions as entirely devoid of empirical content given that: traders are more likely to default when they have large obligations; the pay-off function is likely to be discontinuous; and the liability of the defaulting trader is typically limited (and the CCP's or counterparty's recovery is likely to be costly and include partial recovery at best). Notwithstanding, endogenous default would be a worthwhile extension to the extent that micro-foundations about the strategic incentive to default would more fully capture the link between wealth, price movements and the likelihood of default.
3.3 Traders' Maximisation Problems without a CCP
In the absence of a CCP, the long trader in market m maximises its lifetime utility by
choosing consumption, cm,t, and how many OTC derivatives to trade,
sm,t, in each period. We impose the usual restrictions on the utility
function: 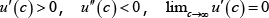 and
and 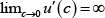 .
.
Formally, the long trader solves:
subject to the flow budget constraint:
The flow budget constraint implies that expenditure on consumption, cm,t, and purchases of OTC derivatives, pm,t sm,t, must be less than or equal to the net value of previous OTC derivatives held, pm,tsm,t − 1, the payment flow received from those OTC derivatives, fm,t sm,t, and the long trader's endowment draw for the period, Am,t.
The short trader in market m solves:
subject to the budget constraint:
3.4 First-order Conditions without a CCP
Solving the two maximisation problems presented in Section 3.3 yields two pricing equations: one for long traders and one for short traders in market m:
and:
These are similar to standard consumption-based asset pricing equations. The price in period
t – for both traders – is equal to the expected discounted value of the OTC
derivative in period t + 1 – namely, pm,t + 1 +
fm,t + 1. This pay-off is discounted by the discount rate
(β) and the stochastic discount factor 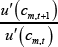 . The
stochastic discount factor measures the relative value of a unit of consumption in the next
period (for a given state) versus a unit of current consumption.
. The
stochastic discount factor measures the relative value of a unit of consumption in the next
period (for a given state) versus a unit of current consumption.
3.5 The CCP
There is one CCP that, unlike traders, has access to all markets. The CCP guarantees full payment of all obligations on OTC derivatives contracts that it clears – in effect, it provides default insurance in the event that a counterparty defaults. Because we assume a continuum of markets and that contract payouts are independent (and statistically independent of λm), a law of large numbers can be applied so that the CCP can correctly forecast its total required payout and is able to collect sufficient resources from participants to cover this payout.[15]
3.5.1 Novation
Traders in market m must centrally clear a market-specific exogenous proportion of their contracts – denoted by λm ∈[0,1]. We model central clearing by having both types of traders sell a proportion λm of their contracts to the CCP in exchange for an exactly offsetting contract with the CCP. That is, the CCP becomes the buyer to every seller and the seller to every buyer (novation). Figure 3 shows the post-novation contractual relationships between long traders, short traders and the CCP.
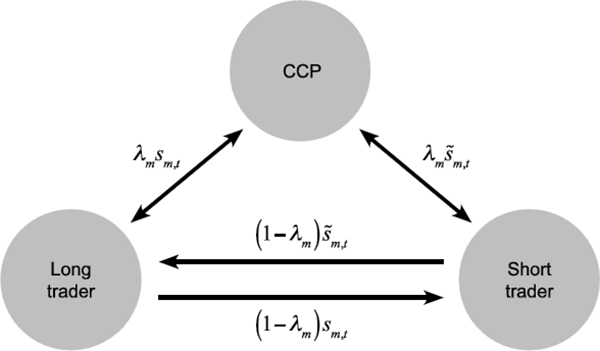
The assumption of a fixed proportion of trades with central clearing partly reflects the G20 commitment to centrally clear all standardised OTC derivatives. At face value, this implies λm = 1. However, in practice, not all derivatives are standardised enough to be centrally cleared, and not all participants are covered by mandates.[16] Nonetheless, the proportion of OTC derivatives covered by existing mandates is substantial in some markets – up to 80 per cent of new trades in the United States (CFTC 2016). In other markets, regulatory mandates are still being developed and so the proportion of trades that are centrally cleared is much lower. The modelling device of a fixed proportion of centrally cleared trades allows us to consider the full spectrum of what might eventually be able to be centrally cleared, including both boundary cases – that is, no central clearing (λm = 0), as was largely the case before the global financial crisis, and full central clearing (λm = 1).[17] Although we consider the full range of λm, we acknowledge that reality is likely to be much closer to 1 than to 0.
3.5.2 The CCP's resources
The CCP must be able to meet its obligations on OTC derivatives it clears. To do so, the CCP charges per-contract initial margin requirements (hereafter margin requirements) and collects default fund contributions from all traders.[18]
The important distinction is that margin posted, λmsm,tZ, is proportional to the number of contracts novated through the CCP, and is returned to a trader if they do not default. In the event of default, only the margin in excess of that required by the CCP to cover the loss is returned to the trader.[19] In contrast, the default fund contribution, λmDFt, does not depend on the number of contracts novated, and can be used to meet losses in cases where the margin posted is insufficient.[20]
In our model, traders do not earn a return on the margin they post. This makes margin costly. This is a realistic feature because CCPs only take high-quality assets to meet margin requirements, typically cash and government bonds. These assets have low yields, and thus posting margin carries an opportunity cost. Having collateral earn no return in our model captures this cost. In Australia, cash and government bonds comprise the majority of margin posted at ASX Clear (Futures) – a domestic derivatives CCP (Cheung, Manning and Moore 2014). These assets have comparatively low yields.
It is useful to define two indicator functions – D and 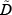 – that indicate whether the long or short trader
defaults:
– that indicate whether the long or short trader
defaults:
It is also helpful to keep track of the direction of payment flows. To this end, we define an indicator function M that denotes whether the long trader is in or out of the money:
The resources that the CCP receives in period t are given by:
There is a negative sign on the 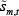 because the CCP collects
margin on both long and short positions.[21]
The gross payments the CCP makes in period t + 1 are given by:
because the CCP collects
margin on both long and short positions.[21]
The gross payments the CCP makes in period t + 1 are given by:
Although a long expression, Equation (13) is intuitive. On contracts in the money for the long trader, the CCP pays out on all contracts that the long trader has novated and collects payments from short traders, except those short traders that default. This captures the first three lines of Equation (13). The next three lines capture the measure of contracts for which the opposite happens – that is, short traders are in the money.
The CCP's budget constraint implies that the resources collected across all markets in period t must be sufficient to meet the CCP's obligations across all markets in t + 1:[22]
Using the CCP budget constraint, an appropriate law of large numbers, and Equations (12) and
(13), we can solve for the period t default fund contribution for any set of
allocations sm,t and 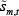 :
:
where 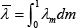 – that is, the average proportion of central
clearing across all markets.
– that is, the average proportion of central
clearing across all markets.
3.6 First-order Conditions and Equilibrium Conditions
We study two solutions to our model. The first is a decentralised solution in which traders choose their own allocations to maximise their utility taking OTC derivative prices, the proportion of OTC derivatives that must be centrally cleared, margin requirements and default fund contributions as given. The second is what we call a ‘constrained-efficient’ solution in which a planner chooses allocations on behalf of all traders in order to maximise social welfare (taking the proportion of trade that must be centrally cleared and margin requirements as given).
As we will show below, the constrained-efficient solution and the decentralised solution are not necessarily the same.[23] The constrained-efficient solution gives us a relevant benchmark for understanding how close different market structures come to the constrained optimum of the economy. Intuitively, one can think of a planner who is choosing the socially optimal level of trade and consumption, subject to the constraints that prices are market determined (markets must clear), that the planner cannot invent new contracts that better hedge risk, and cannot enforce payment in the event of default.
3.6.1 Decentralised equilibrium
The traders' problems are similar to the versions presented in Section 3.3, except that traders must now centrally clear an exogenous fraction of their OTC derivatives contracts. A long trader in market m maximises expected discounted utility by choosing consumption, cm,t, and how many OTC derivatives to trade, sm,t:
subject to the flow budget constraint:
That is, expenditure on consumption, purchases of OTC derivatives, margin requirements and the CCP default fund contribution must be less than or equal to the (net) resources received from OTC derivatives held from the previous period (including the return of margin) and the endowment.
The first-order condition is now:
Although more cluttered than the asset pricing equation without a CCP (Equation (7)), the intuition underlying the long trader's pricing equation is similar: the period t price is the expected discounted value of the contract in period t + 1. This future value comprises:
- the value of the OTC derivative in the next period: pm,t + 1
- payments from the proportion of OTC derivatives that are not centrally cleared: (1 −λm)fm,t + 1
- the net payments to or from the CCP, which depends on whether the long trader is in or out of the money: λm[M(ym,t+1)ym,t+1+(1−M(ym,t+1))fm,t+1]
- the return of margin posted, which is contingent on whether the long trader defaults or not: D(ym,t+1)max(0,Z−[fm,t+1 − ym,t+1])+(1−D(ym,t+1))Z.
Finally, margin requirements reduce the value of the contract today, because every extra contract entered into requires long traders to give up λmZ units of consumption, per contract purchased.
Similarly, the short trader in market m solves:
subject to the flow budget constraint:
where the short trader's budget constraint is slightly different: the signs on margin
requirements are reversed, because the short trader will have 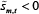 in
equilibrium and the CCP collects margin on the absolute number of contracts sold.[24]
The short trader's pricing equation is thus:
in
equilibrium and the CCP collects margin on the absolute number of contracts sold.[24]
The short trader's pricing equation is thus:
These asset pricing equations nest the non-CCP versions presented in Section 3.4 as a special case; if λm = 0, these conditions collapse to Equations (7) and (8) for the long and short trader respectively.
We now define the conditions that characterise the decentralised equilibrium. Formally, a
decentralised equilibrium is a vector of prices pm,t for each market
m and each time t, a vector of allocations 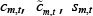 ,
and
,
and 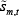 for each market m and each time t,
and a default fund contribution DFt such that:[25]
for each market m and each time t,
and a default fund contribution DFt such that:[25]
- Long and short traders' first-order conditions are met (Equations (17) and (20) respectively).
- The net supply of contracts traded in each market is zero:
- Traders' budget constraints (Equations (16) and (19)) are satisfied.
- The default fund contribution DFt satisfies the CCP's budget constraint (Equation (14)).
We further restrict our attention to time-invariant stationary equilibria, such that sm,t = sm and pm,t = pm∀t. Because the problem is recursive, the stationary equilibrium is the natural one to focus on. Moreover, doing so is consistent with the approach used for other incomplete market models, such as Bewley models.
Dropping the t subscript and denoting variables for the period ahead by primes, we solve for consumption for long traders in market m using the budget constraint (Equation (16)):
For short traders in market m:
For tractability, we assume that all markets have the same λm. This means all markets have the same solution sm. The default contribution charged by the CCP reduces to:
By combining these equations with stationary-equilibrium versions of the pricing equations, we are left with two equations (the two pricing equations) in two unknowns – sm and pm.[26] To solve the system we pick a scalar value of sm and solve for the two state-dependent price vectors pm implied by the two pricing equations (Equations (17) and (20)). This approximation implies that the quantity of contracts traded in each market is not state contingent.[27] Following Edmond and Weill (2012), we use Gauss-Hermite quadrature to approximate the pricing equations. We repeat this process for different values of sm until we find an sm such that the two pricing equations solve for the same price vector. Appendix A.2 contains further details. Because we employ a discrete approximation, many of our results have a step-like shape. We believe this is the result of the approximation, not an underlying feature of the solution. Increasing the granularity of the approximation can mitigate this problem somewhat; however, our baseline calibration with 1,225 states is already computationally expensive.
3.6.2 Constrained-efficient equilibrium
For the constrained-efficient equilibrium, a planner maximises all traders' utility
across all markets by choosing allocations 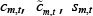 and
and 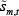 .
The maximisation problem is:
.
The maximisation problem is:
subject to the traders' budget constraints (Equations (16) and (19)), the expression for the default fund contribution (Equation (14)), and the constraint set that all markets must clear. Although the pricing equations for long and short traders are now different to the decentralised case, the approach used to numerically solve for the equilibrium is otherwise identical. Appendix B contains the Lagrangian, pricing equations and solution method for this problem. It should be noted that this benchmark is constrained-efficient in the sense that it is optimal subject to constraints of imperfect contracting (reflected in the non-unitary negative correlation between contract payouts and endowment risk), and that payment in the event of default cannot be enforced.
3.7 Calibration and Welfare
The model is calibrated to quarterly data because the majority of interest rate OTC derivatives – by far the largest and most important product in the Australian OTC derivatives market – have quarterly coupon payments. Table 1 outlines the baseline calibration.
We choose β= 0.9975 to match a 1 per cent annual rate of time preference, as in Edmond and Weill (2012); we use a constant relative risk aversion utility function, with a coefficient of risk aversion γ= 4, as is common in asset pricing literature. We choose σA to match the standard deviation of Australian aggregate household final consumption expenditure growth (0.8 per cent) to the standard deviation of trader consumption in the no-clearing version of the model. We set σy = σA without loss of generality. Traders would simply scale up or down their purchases of contracts if we changed the variance of the payout of OTC derivatives.
| Parameter | Value | Description |
|---|---|---|
| γ | 4.0 | Risk aversion |
| β | 0.9975 | Discount rate |
| σA | 0.0106 | Standard deviation in endowment payments |
| σy | 0.0106 | Standard deviation in OTC derivatives contract payments |
| corr(ym,t,Am,t) | −0.7 | Correlation between endowment and financial contract payments |
| Ā | 1.0 | Mean endowment payment |
| yupper | 2.57σy | Upper threshold, above which long traders default |
| ylower | −2.57σy | Lower threshold, below which short traders default |
| λm | 0.5 | Mandatory fraction of contracts novated through CCP |
| Z | 2.33σy | Margin required per contract |
We choose the correlation between ym,t and Am,t as −0.7 for the baseline. This implies that the OTC derivative payout will move in the same direction as the endowment payout about 25 per cent of the time, in which case the hedge will be ineffective. In the absence of detailed proprietary data it is very difficult to ascertain the average level of basis risk traders face when hedging with OTC derivatives. Accordingly, we explore a range of basis risk scenarios with correlations ranging from -1 (no basis risk/a perfect hedge) to zero (the hedge is completely ineffective).
For the mean endowment payment, Ā, we normalise this value to 1. Since default is only linked to price movements relative to the default thresholds (and is unrelated to Ā), the mean endowment payment has no effect on prices or trade allocations once we condition on the variance of consumption growth through σA, and given the assumption of constant relative risk aversion.
We set baseline margin, Z, at 2.33 standard deviations of Am,t. This level of margin coverage is consistent with the Principles for Financial Market Infrastructures (PFMI) requirement that CCPs collect margin sufficient to cover a single-tailed confidence level of at least 99 per cent of estimated future price movements (CPSS-IOSCO 2012).
For the default thresholds, we choose upper and lower bounds at ±2.57 standard deviations of Am,t, implying a quarterly rate of default of about 1 per cent (half comprising long trader defaults, half short trader defaults). Again, actual default rates are very difficult to calculate without good data. In the analysis that follows, we explore a range of default rates.
In our baseline we set λm = 0.5, implying that half of all OTC derivatives must be centrally cleared. This choice is guided by the fact that roughly half of all OTC interest rate derivatives are currently centrally cleared globally. The proportion is a bit lower in Australia – around a quarter of outstanding interest rate derivatives denominated in Australian dollars were centrally cleared as of August 2015, but more than half of outstanding interest rate derivatives denominated in G4 currencies were. A much higher proportion of new trades is centrally cleared (APRA et al 2015). In the United States – which has mandatory central clearing requirements in effect – around 80 per cent of all new interest rate derivatives are centrally cleared (CFTC 2016). We also experiment with different values for mandatory clearing in the analysis that follows.
We measure social welfare by the unconditional mean of aggregate welfare, and equally weight the utility of all traders:
In the results that follow, it is measured as the percentage lump-sum consumption transfer each period that makes traders indifferent between welfare in the relevant equilibrium we are studying (i.e. W) and a constant mean consumption stream (i.e. absent any risk).
4. Results
4.1 The Value of OTC Derivatives
OTC derivatives are valuable because they enable traders to hedge their idiosyncratic endowment risk and reduce the variance of their consumption. Because traders are risk averse, these hedges are valuable and provide a motivation for trade. The left-hand panel of Figure 4 highlights the result that the benefits of OTC derivatives are highest when they provide a more effective hedge – that is, when the correlation between the contract payment (ym,t) and the idiosyncratic endowment stream (Am,t) is more negative (approaches minus one). As the correlation between Am,t and ym,t becomes weaker (less negative), traders' hedges are less effective at reducing their consumption variance. In the extreme, with zero correlation, OTC derivatives have no social welfare value because traders cannot use them to reduce the variance of their consumption.
The right-hand panel of Figure 4 highlights the result that, as the probability of default rises (and so counterparty credit risk increases), the benefit of OTC derivatives falls. Default has two effects. First, default means that traders do not get paid when the ym,t movement is most favourable, because their counterparty defaults. On the other hand, because default is symmetric, traders do not have to pay when they receive a very adverse ym,t. The former effect outweighs the latter because the contract pay-off is negatively correlated with the endowment and utility is concave. This means that short traders default when long traders' endowment draws are low (on average), and the marginal utility of long traders' consumption is high. In contrast, the marginal utility of consumption of the short trader defaulting is low since they received a favourable endowment draw (on average), but do not have to pay if there is a large adverse price movement. This asymmetry means that higher default probabilities reduce the value of OTC derivatives.
When traders cannot default and the correlation between the contract pay-off ym,t and the endowment Am,t is equal to −1, traders can offset all endowment risk. This is equivalent to the complete markets solution to our model and is the first-best optimum.
Notes: For both panels – the welfare gains are calculated assuming no central clearing, in which case the constrained-efficient and decentralised solutions are identical; for the left-hand panel – two-sided default probability is 1 per cent; for the right-hand panel – corr(ym,t, Am,t) = −0.7
4.2 Effects of a CCP on Trade and Welfare
4.2.1 Default fund: insurance against default
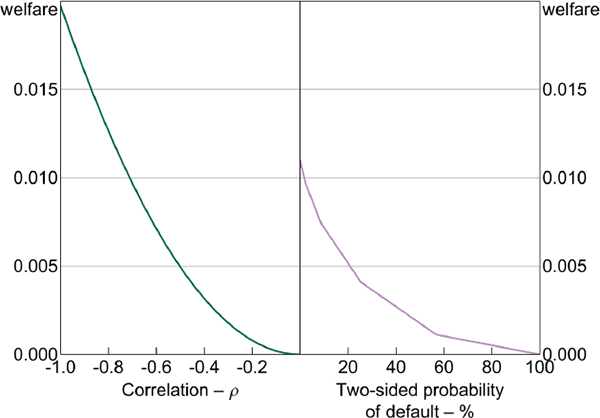
We now introduce central clearing and examine how the key parameters of our model affect welfare and allocations. Figure 5 shows the effect of increasing the fraction of trades centrally cleared, under both the decentralised and constrained-efficient equilibria – that is, increasing λm. For this comparison, the CCP only uses the lump-sum default fund contribution; we discuss the role of margin in further detail below.
The results highlight that the effect of central clearing depends on whether a decentralised or constrained-efficient solution is used. In the constrained-efficient solution, increasing central clearing monotonically increases welfare – full clearing is optimal. The effect on OTC derivative trade is relatively small.[28] This is because additional central clearing increases the fraction of contracts that are insured, and so are a better hedge. In the constrained-efficient solution prices adjust to incorporate the additional marginal cost of this insurance incurred by the CCP, and so there is no trade distortion. Central clearing is beneficial because it efficiently mutualises credit risk in the constrained-efficient equilibrium.
Notes: The CCP collects no margin; the two-sided default probability is 1 per cent; welfare is relative to no clearing
The results for the decentralised equilibrium are quite different. Increasing λm leads to a fall in social welfare and a large increase in the number of contracts traded. The reason is that, although traders privately value additional novated contracts that are free of counterparty credit risk, the value to society of these contracts is negative in the absence of any mechanism to price the additional insurance the CCP provides. When only the default fund is used to fund payouts, the marginal decision of any trader to trade more OTC derivatives fails to internalise the cost of the trader's own default on the CCP's cost of providing insurance. We refer to this as a ‘mutualisation externality’. It is similar to a moral hazard problem, where insuring an agent against risky activity can lead to the agent undertaking more of that activity.
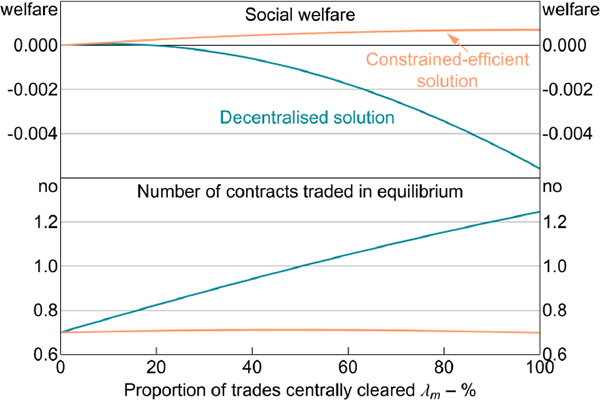
Figure 6 highlights the relationship between the effectiveness of the hedge and the social value of central clearing in the constrained-efficient equilibrium (top-left panel). A CCP is more valuable to traders when the contract is a more effective hedge – that is, when the correlation between endowment payouts and OTC derivative payouts is more negative. When the correlation is very negative, counterparty default occurs at the same time traders receive adverse endowment draws, on average. This is when the payments on the contract are most valuable and, therefore, when the CCP's insurance is most valuable.
Notes: The CCP collects no margin; for left-hand panels – two-sided default probability is 1 per cent, welfare gains are relative to the welfare of the no clearing equilibrium, given the relevant correlation; right-hand panels show welfare difference between full clearing (λm = 1) and no clearing (λm = 0)
A similar intuition underlies the probability of default (Figure 6, top-right panel). Default reduces hedge effectiveness and therefore welfare; the higher the probability of default, the greater the welfare loss. Since the CCP never defaults, it therefore reduces these welfare costs. Examining the interaction between default and the correlation in contract payouts, we see that central clearing is most valuable when the probability of default is high and OTC derivatives would otherwise provide an effective hedge against idiosyncratic risk. In this case, traders place a high value on the insurance against counterparty default provided by the CCP. In contrast, when either the probability of default is low, or OTC derivatives are only an ineffective hedge, the welfare gains from central clearing are small.
The bottom panels of Figure 6 tell the same story as Figure 5. Although the same benefits from central clearing are present in the decentralised equilibrium as in the constrained-efficient equilibrium, the cost of the mutualisation externality is much larger than these benefits. As a result, in the decentralised equilibrium, central clearing can reduce welfare, particularly when default is likely (Figure 6, bottom-right panel).
4.2.2 The mutualisation of default losses
Figure 5 showed that traders choose to trade an inefficiently large number of contracts in the decentralised equilibrium as the fraction of trades required to be centrally cleared increases. This inefficiency arises because traders do not consider the costs that their own default imposes on the CCP. These costs raise the required default fund contribution for all traders. In effect, traders are taking advantage of the asymmetry in the pay-off structure for centrally cleared contracts – traders can default, but the cost of ensuring that the CCP never defaults is mutualised.
In contrast, the constrained-efficient solution internalises the costs of traders' defaults on the CCP. The terms on the last line of Equation (27) show the difference between the pricing equation derived from the decentralised version of the model and the constrained-efficient version for the long trader in market m.[29]
This wedge, which we call the ‘mutualisation externality’, comprises:
-
The expected difference between what the CCP will have to pay the long trader when the long
trader is in the money (ym,t) and the payment the
CCP expects to receive from the long trader when the long trader is out of the
money(fm,t):
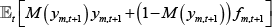 .
.
-
Any offsetting margin:
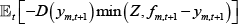 . This term reduces the loss the
CCP suffers by either: the full amount fm,t + 1 − ym,t
+1 if the loss is less than the posted margin; or Z if the margin is not
sufficient to cover the loss.
. This term reduces the loss the
CCP suffers by either: the full amount fm,t + 1 − ym,t
+1 if the loss is less than the posted margin; or Z if the margin is not
sufficient to cover the loss.
-
The marginal social value of any increase in the expected difference between payouts and
collections:
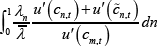 .
.
Internalising the mutualisation externality reduces the value of OTC derivatives to a trader and therefore leads to fewer contracts traded in equilibrium.
The mutualisation externality is increasing in the probability of default (Figure 7, right-hand panels). This result is intuitive – a higher probability of default increases the expected difference between M(ym,t)ym,t and (1 − M(ym,t))fm,t, and therefore increases the size of the externality. In contrast, correlation has little effect on the size of the mutualisation externality (Figure 7, left-hand panels). Although a weaker (less negative) correlation implies a slightly larger externality, the effect is negligible.
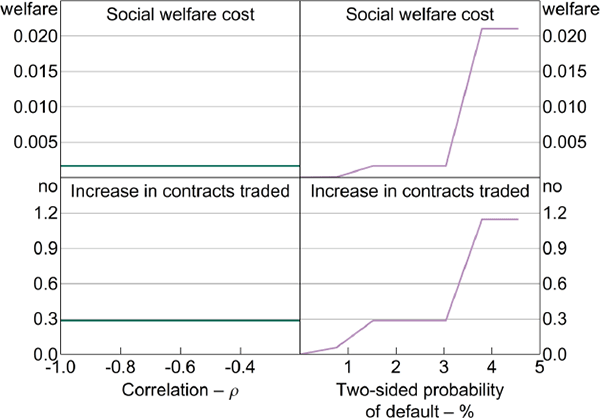
Notes: Welfare cost and the increase in contracts traded measured relative to the constrained-efficient equilibrium for the relevant parameters; for all panels – the CCP collects no margin, λm = 0.5; for the left-hand panels – two-sided default probability is 1 per cent; for the right-hand panels – corr(ym,t, Am,t) = −0.7
4.2.3 The role of margin
It is straightforward to show that the mutualisation externality could be exactly corrected by levying market-by-market state-contingent taxes on contracts. The efficient state-contingent tax would need to be set equal to the terms on the last line of Equation (27). In practice, these taxes do not exist. But CCPs do collect margin.
Margin requirements act like an implicit tax because the collateral posted to meet the requirements does not earn a return in our model. This makes margin costly because current consumption is more valuable than future consumption. Margin is also costly in reality, because the low yields on collateral-eligible assets imply an opportunity cost. However, margin requirements and taxes are not identical. With margin, traders give up resources today, but have their resources returned if they do not default, and so margin requirements affect both the cost and the pay-off structure of OTC derivatives. In contrast, a tax is never returned – it affects only the cost of trade today.
Figure 8 highlights that higher margin requirements (measured relative to the standard deviation of ym,t) induce traders to trade fewer contracts in both the decentralised equilibrium and constrained-efficient equilibrium by increasing the cost of trade. The effect is strongest in the decentralised equilibrium, which has a lot more trade absent any margin requirements. Importantly, higher margin requirements reduce the welfare gap between the constrained-efficient equilibrium and decentralised equilibrium. This is because the implied increase in the cost of trade, although not identical to an optimal state-contingent tax, does a good job of replicating its effects.
Accordingly, the overall level of trade converges from an inefficiently high private level without margin, towards the social optimal level as margin requirements are raised.[30]
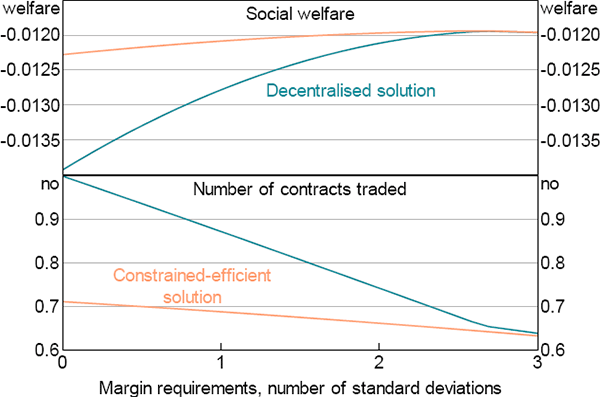
Notes: λm = 0.5, two-sided default probability is 1 per cent; decentralised welfare measure is adjusted for the initial endowment of margin; welfare is measured relative to the welfare from a constant stream of consumption equal to Ā
Figure 9 shows the margin requirements that maximise social welfare in the decentralised solution as a function of the probability of default. It implies that CCPs should set higher margin requirements as the probability of default increases, which is intuitive given that the size of the mutualisation externality increases as the probability of default increases (Figure 7).
Figure 10 highlights that, with appropriately set margin requirements, welfare in equilibria with full clearing is higher than that with no clearing for all possible correlations and default rates considered. Moreover, the welfare gain between the two equilibria is higher the more negative the correlation between the contract and endowment payouts (i.e. the more effective the hedge for a given rate of default) and the higher the probability of default (for a given contract correlation). Nonetheless, this figure does not answer the question of whether full clearing is always socially optimal, as an interior λm could potentially yield higher welfare. This is the question we now address.
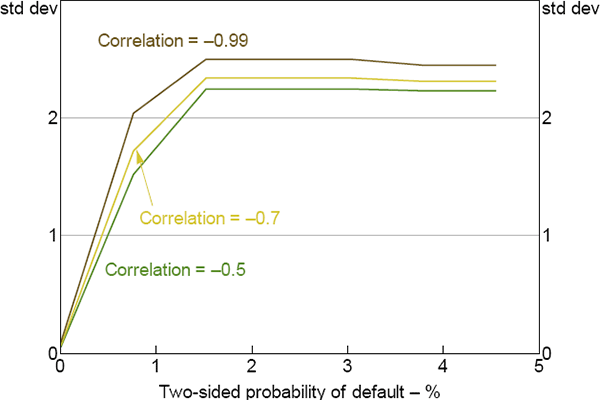
Note: λm = 0.5
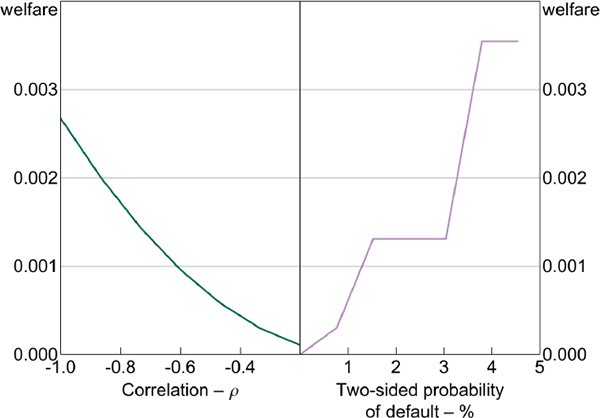
Notes: For the left hand panel – two-sided default probability is 1 per cent; for the right hand panel – corr(ym,t, Am,t) = −0.7
4.3 Optimal Central Clearing
For the optimal level of central clearing, we numerically maximise social welfare over two parameters jointly: the proportion of contracts that must be centrally cleared and required margin, which we now refer to as optimal margin. We also consider cases where margin requirements are held fixed at either zero margin, low margin (covering 90 per cent of the one-tailed moves in ym,t), PFMI margin (99 per cent of one-tailed coverage) or high margin (99.9 per cent one-tailed coverage).
Figure 11 shows the fraction of central clearing (λm) that maximises social welfare in a decentralised equilibrium.[31] Consistent with the constrained-efficient results in Figure 5, if margin requirements are set optimally, full clearing is always welfare maximising (the top panel of Figure 11). This reflects the result that optimal margin in a decentralised equilibrium can provide a good approximation of the constrained-efficient equilibrium.
On the other hand, if margin requirements are not set optimally, full clearing may be less than optimal:
- If margin requirements are set too high, full clearing will lead to too little hedging. The ‘high margin’ line in Figure 11 shows this effect: when the probability of default is low, high margin is needlessly expensive, which makes central clearing too costly relative to its insurance benefits.
- If margin requirements are set too low, the severity of the mutualisation externality will overwhelm the benefits of central clearing. This effect can be seen in the ‘ zero margin’ and ‘ low margin’ lines in Figure 11. At low default probabilities, low margin requirements are near optimal and so the welfare-maximising level of mandatory central clearing is high. But, as the probability of default rises, the mutualisation externality becomes too acute. In these cases, mandatory central clearing obligations will have the opposite of the intended effect: participants will take on too much risk by trading an inefficiently large number of contracts.
Figure 12 shows how the social welfare-maximising proportion of central clearing depends on the correlation between the endowment (Am,t) and the OTC derivatives contract (ym,t). With the exception of optimal margin, the welfare-maximising fraction of mandatory central clearing decreases as the OTC derivative becomes a less effective hedge.
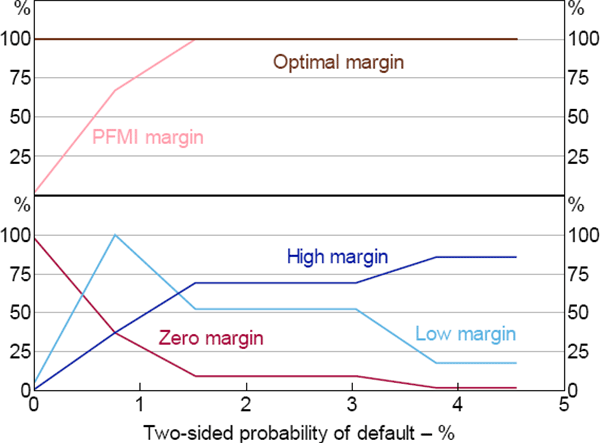
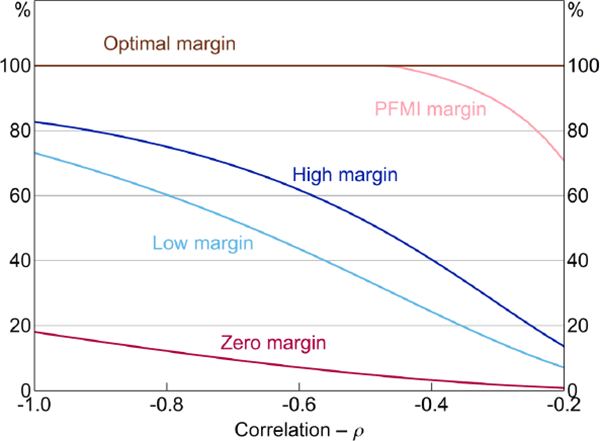
4.4 Implications and Caveats
A key implication of our findings is that the efficiency of central clearing depends on how close margin is to its optimal level. If margin requirements are set too low, the moral hazard problem embedded in central clearing can be substantial and mandatory central clearing can be very inefficient. Similarly, if set too high, margin makes trading too expensive and, thus, mandatory central clearing inefficiently reduces risk sharing in this case.
A second implication of our findings is that the case for mandatory central clearing is strongest for asset classes that are closely correlated with banks' underlying risk – for any initial margin requirements (Figure 12). To the extent that banks are the focus of OTC derivatives reforms, this observation suggests that the case for mandatory clearing requirements for interest rate, foreign exchange and credit derivatives is stronger than other asset classes. To date, policymakers have indeed focused on interest rate and credit derivatives.
Third, quantitatively our model suggests that current international standards that require CCPs to set margin to cover at least 99 per cent of one-tailed movements, or 2.33 standard deviations in our model, are very close to the optimum margin requirement in the decentralised equilibrium when the probability of default is 2 per cent or more (Figure 9). At lower rates of default, less than full clearing becomes optimal when PFMI margin requirements are applied (Figure 11).
Of course, a good deal of caution is required in drawing inference from these results to real-world policy. Our model is highly stylised and abstracts from many crucial features that policymakers must additionally consider. For example, the only costs of central clearing in the model are the mutualisation externality and the opportunity cost of the collateral posted as margin. In practice, there are many other policy-relevant costs associated with central clearing. Setting up and maintaining a relationship with a CCP is time-consuming and expensive, and requires a high degree of operational sophistication – far more so than establishing a bilateral trading relationship. For many market participants, these costs make central clearing prohibitively expensive. These costs also depend on the type and size of the market participant; our model abstracts from this type of heterogeneity. Central clearing is also liquidity intensive; not all market participants are well-suited to manage the associated costs and risks. All these factors suggest that not all participants are like those in our model.
Similarly, there may be additional reasons why not all products are suitable for clearing, which our model cannot see. For instance, although our model suggests there may be gains from mandatory clearing of foreign exchange OTC derivatives – because this asset class is likely to be correlated with banks' assets and liabilities – central clearing of foreign exchange derivatives faces technology and infrastructure hurdles that have not yet been solved. These hurdles are policy relevant, but not considered here.
Finally, our model does not consider some of the benefits of central clearing. For instance, our model says nothing about the netting or financial-stress benefits that central clearing brings about by simplifying the financial network, nor does our model say anything about the benefits from having coordinated default management. These benefits have been extensively covered in the literature, so we have not addressed them here.
5. Conclusion and Discussion
This paper provides a tractable framework for assessing the efficiency of mandatory clearing and optimal margin requirements using a consumption-based asset pricing model with market segmentation. We view it as a useful first step in understanding how trader behaviour might respond to different market structures and for evaluating different public policy interventions designed to improve welfare and stability in OTC derivative markets.
Our analysis suggests that:
- Central clearing can improve welfare by mitigating counterparty credit risk in OTC derivatives markets.
- The benefits of central clearing are higher the higher the probability of default and the stronger the correlation between the OTC derivatives contract and the underlying risk – that is, when OTC derivatives are an effective hedge.
- In the absence of initial margin, the moral hazard problem that arises from mutualising default losses through a CCP's default fund is large. This inefficiency can outweigh the benefits from central clearing and worsens as the probability of default rises.
- Initial margin requirements are an effective tool to mitigate this externality and are a good substitute for state-contingent taxes. If margin requirements are set optimally, central clearing is always welfare improving. Optimal margin requirements are higher when default is more likely.
- The optimal level of central clearing is sensitive to how margin requirements are calibrated.
Appendix A: Trader Behaviour and Solution Method
A.1 Lagrangians
The Lagrangian for the long trader is:
where μm,t is the Lagrange multiplier on the period t budget constraint for a long trader in market m. This equation is maximised by choice of cm,t and sm,t.
The short trader is similar:
The first-order conditions from these problems yield Equations (17) and (20) in the main text.
A.2 Numerical Methods
We solve the system by first picking a scalar sm and then solving each pricing equation for a stationary price vector. Restricting attention to equilibria where the quantity of trade is not state contingent considerably simplifies the computational burden of the problem. We approximate the expectation on the right-hand side of the pricing equation using Gauss-Hermite numerical integration. The price vector is the discretised numerical approximation of the state-dependent price function. We use 35 quadrature nodes for both Am,t and ym,t, which means we have a total of 1,225 states. We use such large numbers because most of the action in our model occurs in the tails. This means that we need a large state space to ensure smooth coverage of the tails, particularly when we vary parameters like margin requirements: smaller state spaces mean that there are large discrete jumps as margin requirements or default bounds move past one of the tail quadrature nodes.
Solving the system then amounts to finding a scalar value of sm such that price vector solutions to the two pricing equations are approximately the same. We find this value of sm using a numerical nonlinear solver. In all cases we assume λm = λ for all m. This greatly simplifies the solution method, because all markets are identical. We need to solve for only one sm, because this will be a solution for all the markets.
The equilibrium solution to our model (without collateral) is always an sm
such that the price for both agents is zero. This is consistent with real-world practice: most
OTC derivatives have zero net present value when agreed on.[32] This is an intuitive
result, traders are trading the contract so that their consumption (which depends on
sm) is uncorrelated with the payoff of the contract. Because of the symmetry
in long and short traders' optimisation programs, the sm that ensures
this is the case for both traders is the same (noting that 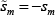 ).
).
In some cases we need to evaluate integrals across all markets, for example, for the stationary equilibrium CCP default fund fee (Equation (24)). We do so by relying on the fact that draws of ym and Am are independent of sm and that both ym and Am are independent and identically distributed and uncorrelated with other markets (i.e. corr(Am, An) = 0). These assumptions allow us to use a law of large numbers such that:
which we evaluate by a Gauss-Hermite quadrature rule in the same way as outlined above.
In principle, we can also solve for a state-contingent vector for sm, and focus on the first moment of this distribution. Numerically, this is a much more computationally demanding problem because we quickly run into the curse of dimensionality when jointly maximising welfare over λm and Z. Nevertheless, to see if our results are sensitive to our simpler solution method we compared the first moment of the solution with a given distribution for sm with the non-state-contingent solution. The results are similar in this case.
Appendix B: Solving the Constrained-efficient Problem
As described in Section 3.6.2, the planner maximises all traders' utility, taking into account all traders' budget constraints, and the CCP's budget constraint. The Lagrangian for the problem is:
This equation is maximised by choice of 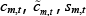 and
and 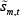 for all m ϵ [0,1].
for all m ϵ [0,1].
The first-order conditions for market m give two pricing equations, one for the long trader and one for the short trader:
The solution method for finding the stationary equilibrium is identical to that used for the decentralised equilibrium.
References
Acharya V and A Bisin (2014), ‘Counterparty Risk Externality: Centralized Versus Over-The-Counter Markets’, Journal of Economic Theory, 149, pp 153–182.
Allen F and D Gale (2000), ‘Financial Contagion’, Journal of Political Economy, 108(1), pp 1–33.
Anderson S, JP Dion and H Perez-Saiz (2013), ‘To Link or Not to Link? Netting and Exposures between Central Counterparties’, Journal of Financial Market Infrastructures, 1(4), pp 3–29.
APRA, ASIC and RBA (Australian Prudential Regulation Authority, Australian Securities and Investments Commission and Reserve Bank of Australia) (2015), Report on the Australian OTC Derivatives Market, Council of Financial Regulators, Sydney.
ASIC (2015), ASIC Derivative Transaction Rules (Clearing) 2015, December.
Australian Treasury (2015), Corporations (Derivatives) Amendment Determination 2015 (No. 1), August.
Biais B, F Heider and M Hoerova (2012), ‘Clearing, Counterparty Risk, and Aggregate Risk’, IMF Economic Review, 60(2), pp 193–222.
Carter L, J Hancock and M Manning (2015), ‘Ownership, Incentives and Regulation of CCP Risks’, in M Diehl, B Alexandrova-Kabadjova, R Heuver and S Martínez-Jaramillo (eds), Analyzing the Economics of Financial Market Infrastructures, Advances in Finance, Accounting, and Economic (AFAE), IGI Global, Hershey, pp 272–303.
CFTC (Commodity Futures Trading Commission) (2016), ‘Weekly Swaps Report’, Release date: 23 March, viewed 30 March 2016.
Cheung B, M Manning and A Moore (2014), ‘The Effective Supply of Collateral in Australia’, RBA Bulletin, September, pp 53–66.
CPMI-IOSCO (Committee on Payments and Market Infrastructures and Board of the International Organization of Securities Commissions) (2014), Recovery of Financial Market Infrastructures, Bank for International Settlements, Basel.
CPSS-IOSCO (Committee on Payment and Settlement Systems and Technical Committee of the International Organization of Securities Commissions) (2012), Principles for Financial Market Infrastructures, Bank for International Settlements, Basel.
Duffie D and H Zhu (2011), ‘Does a Central Clearing Counterparty Reduce Counterparty Risk?’, The Review of Asset Pricing Studies, 1(1), pp 74–95.
Edmond C and P-O Weill (2012), ‘Aggregate Implications of Micro Asset Market Segmentation’, Journal of Monetary Economics, 59(4), pp 319–335.
FSB (Financial Stability Board) (2015), ‘OTC Derivatives Market Reforms: Tenth Progress Report on Implementation’, November.
Gibson M (2013), ‘Recovery and Resolution of Central Counterparties’, RBA Bulletin, December, pp 39–48.
Haene P and A Sturm (2009), ‘Optimal Central Counterparty Risk Management’, Swiss National Bank Working Paper No 2009-7.
Heath A, G Kelly and M Manning (2013), ‘OTC Derivatives Reform: Netting and Networks’, in A Heath, M Lilley and M Manning (eds), Liquidity and Funding Markets, Proceedings of a Conference, Reserve Bank of Australia, Sydney, pp 33–73.
Heath A, G Kelly and M Manning (2015), ‘Central Counterparty Loss Allocation and Transmission of Financial Stress’, RBA Research Discussion Paper No 2015–02.
Heath A, G Kelly, M Manning, S Markose and A Rais Shaghaghi (forthcoming), ‘CCPs and Network Stability in OTC Derivatives Markets’, Journal of Financial Stability.
Heller D and N Vause (2012), ‘Collateral Requirements for Mandatory Clearing of Over-The-Counter Derivatives’, BIS Working Paper No 373.
Jackson JP and M Manning (2007), ‘Comparing the Pre-Settlement Risk Implications of Alternative Clearing Arrangements’, Bank of England Working Paper No 321.
Koeppl TV and C Monnet (2008), ‘Central Counterparties’, Center for Financial Studies CFS Working Paper No 2008/42.
Koeppl TV and C Monnet (2010), ‘The Emergence and Future of Central Counterparties’, Queen's Economics Department Working Paper No 1241.
Koeppl TV, C Monnet and T Temzelides (2012), ‘Optimal Clearing Arrangements for Financial Trades’, Journal of Financial Economics, 103(1), pp 189–203.
Neklyudov A and B Sambalaibat (2015), ‘Search, Clientele, and Dealer Networks’, Paper presented at Federal Reserve Bank of St. Louis 2015 Summer Workshop on Money, Banking, Payments, and Finance, St Louis, 10–14 August.
Pirrong C (2009), ‘The Economics of Clearing in Derivatives Markets: Netting, Asymmetric Information, and the Sharing of Default Risks Through a Central Counterparty’, Unpublished manuscript, University of Houston, January.
Acknowledgements
We would like to thank Anthony Brassil, Pedro Gomis-Porqueras, Chris Edmond, Shuyun May Li, Mark Manning, Bruce Preston, John Simon and seminar participants at Monash University and the University of Melbourne for comments and helpful suggestions. The views expressed in this working paper are those of the authors and do not necessarily reflect the views of the Reserve Bank of Australia or the University of Melbourne. The authors are solely responsible for any errors.
Footnotes
Reserve Bank of Australia and University of Melbourne [*]
Economic Research Department, Reserve Bank of Australia [**]
As of November 2015, 12 of 24 Financial Stability Board member jurisdictions have a legislative framework in force for mandatory central clearing requirements (FSB 2015). [1]
Although private market default insurance exists in the real world – in the form of credit default swaps (CDS) – single-name CDS exist only for fairly large institutions. Moreover, the protection buyer is still exposed to the credit risk of the counterparty on the CDS. Bilateral initial margin can also provide a form of default insurance, though it is only partial. We do not consider bilateral margining in this paper. [2]
However, electronic platforms are becoming increasingly common for some of the very commonly traded OTC derivatives, like US dollar interest rate swaps. [3]
Bilateral margin can also provide partial protection; however, we do not consider it in this paper in order to keep the model simple, and to focus on our key research question. [4]
CCPs also contribute their own equity to the default fund, although this is typically small relative to participant contributions. [5]
The distribution underlying this exposure is modelled by the CCP and is typically based on historical price data. [6]
This requirement only applies to systemically important CCPs; non-systemically important CCPs need to cover the largest single participant. The three OTC derivatives CCPs licensed in Australia all meet the ‘cover two’ standard. [7]
For the rest of this paper, we abstract from concerns about CCP default because it does not change the underlying insights of the model. [8]
Bilateral margin may not cover the full extent of the loss; CDS have counterparty credit risk associated with respect to the protection seller. [9]
We use a normal distribution, rather than a log-normal distribution (as is common in asset pricing literature), because long and short traders are on opposite sides of the distribution, and so we need a symmetric distribution. However, it does imply a very low probability of negative consumption. In practice, our calibration is such that this would be in the order of a 100 standard deviation event. Our numerical approximation ignores such unlikely events. [10]
Without loss of generality, we restrict attention to corr(εm,t, ym,t) < 0. The negative correlation implies that long traders will want to buy OTC derivatives to offset their Am,t risk; short traders will want to sell (i.e. have negative holdings) to offset their Ãm,t risk, hence our ‘long’ and ‘short’ terminology. [11]
Consistent with our incomplete markets set-up, we do not permit traders to agree on contracts that would otherwise circumvent our default mechanism. [12]
In addition, we do not assume explicit bankruptcy costs; nonetheless, as we will show, default is still welfare reducing because it reduces the effectiveness of the OTC derivatives hedge. [13]
This did not substantially change the qualitative results, although it naturally affected the quantitative results.
[14]Alternatively, if one implicitly assumes that a CCP has a small residual of its own equity, this will be sufficient to cover any deviation between the expected payout and the actual payout without affecting the CCP's viability. [15]
For instance, in Australia only internationally active dealers are covered by the current mandate. [16]
In effect, we assume that the regulatory mandate binds, and that traders would choose to clear fewer contracts in the absence of the mandate. There may be other equilibria where traders optimally choose to clear more than the regulatory mandate, but we do not focus on these because any proposed change in regulation would not affect allocations or welfare. A richer model, in which traders could choose whether to clear a contract not covered by regulatory mandates, could shed further light on whether the regulatory constraint is likely to bind in the first place. [17]
Because we calibrate our model to quarterly data, we abstract from high frequency changes in variation margin. [18]
In our model, the possibility of having more margin than loss only occurs when the margin requirement is set higher than the default threshold. We consider parameter values where this is and is not the case in our analysis. Both have occurred in recent practice: SwapClear was able to close out the Lehman Brothers portfolio in 2008 without exceeding margin; KRX had to use some of its default fund in handling the default of HanMag Securities in 2014 (although this was a futures default, not an OTC derivatives default). [19]
In reality, CCPs scale default fund requirements based on traders' activity through the CCP. However, re-sizing occurs much less frequently than initial margin is called for, and so has less immediate incentive effects. [20]
And, in equilibrium, it will be the case that 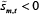 .
[21]
.
[21]
We will assume that this constraint binds in equilibrium. In effect this will imply that the CCP cannot earn positive economic profits in equilibrium (i.e. cannot extract a monopoly rent through its default contribution charge). As we note below, the CCP can exactly forecast required payouts because there is a continuum of markets. [22]
However, the constrained-efficient solution can be implemented in a decentralised equilibrium by taxing contracts on a market-by-market basis. This can be seen formally in Section 4.2.2, Equation (27). [23]
The market clearing constraint together with constant relative risk aversion utility and
the sign normalisation corr(εm,t,ym,t)<0
ensure that 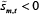 in equilibrium.
[24]
in equilibrium.
[24]
This is an abuse of notation, but reflects that we discretise the problem to solve it
numerically. More formally, prices and allocations at time t and market
m are time invariant functions: 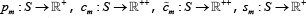 and
and 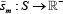 , where the state space
, where the state space 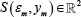 is defined for each market m ∈[0,1].
[25]
is defined for each market m ∈[0,1].
[25]
Strictly, we have infinitely many equations, because we have two equations for each market. However, all markets are identical; solving one market solves all of them. [26]
Numerically, the errors from using a non-state-contingent solution are small; see Appendix A. [27]
The number of contracts increases very slightly – about 1 per cent between no clearing and full clearing. [28]
See also Appendix B. [29]
Note that the small increase in social welfare in the constrained-efficient solution reflects the effect of margin on the steady state of the economy, and not a correction in the pricing of OTC derivative contracts. [30]
We focus only on the decentralised equilibrium because traders' responses are important for the optimality of any real-world market structure reform. [31]
There are a few exceptions, such as market-agreed coupon interest rate swaps and standardised credit index derivatives. [32]