RBA Annual Conference – 2007 Discussion
Chris Carroll
Nothing beats the permanent income hypothesis (PIH) as a starting point for discussing a paper on consumption and debt choices.[1] If total wealth O is the sum of market wealth b and human wealth h, the perfect foresight incarnation of the PIH says that spending is proportional to O:[2]

where, if income is expected to grow at rate g, the human wealth component is

Even in this rudimentary form, the model already has an interesting implication; a change in households' beliefs about the future income growth rate could have a powerful effect on spending (the ‘human wealth effect’ of growth). While there is some ambiguity about the appropriate measure of interest rates, it is clear that the quantity r − g will be substantially altered by even modest changes in beliefs about growth.
This provides a first example of the authors' wide-ranging empirical methodology. Rather than indulging in vague speculations about whether perceptions of growth might have changed, or (even worse) estimating a structural macroeconometric model that forces expectations to match some currently popular theory, the authors resort to a simple alternative; they report households' actual measured expectations. (It turns out that the University of Michigan's monthly survey of consumers has asked households a direct question on this subject since the 1950s.) The results provide no support for the proposition that soaring optimism explains the decline in the saving rate in the United States depicted in their first figure; in fact, in the reported figures, the median household seems to have become marginally less optimistic over the relevant period.[3]
Another possibility implied by the equations above is that, holding growth expectations constant, a decline in real interest rates r will increase the present discounted value of future labour income, thereby encouraging more consumption today (the human wealth effect of interest rates). This possibility is given additional plausibility by a real-world fact that is not captured in the model; loan repayment rates are generally determined using nominal, not real, rates, so a decline in inflation could reduce household debt service burdens (and encourage higher debt levels) even if real rates were unaffected (Debelle 2004).
Interest rates are the one factor emphasised in every model but on which the authors offer no new evidence. They diffidently mention that according ‘to some of the empirical models of aggregate consumption used at the Federal Reserve Board, the net decline in real interest rates during the past half-dozen years can explain about 2 percentage points of the decline in the aggregate saving rate over that period’, but a footnote then undermines even this modest claim. I am sympathetic to their reluctance to say more, which I suspect reflects a justified view that the existing literature on interest rate effects is thoroughly unpersuasive. However, it would have been interesting to see some alternative evidence about interest rate expectations from the consumer sentiment surveys or the Survey of Consumer Finances (SCF) data. At the very least they could report that an examination of those sources produced nothing useful, which would itself be a useful fact.
We have not yet exhausted the implications of the PIH framework. With perfect foresight and a utility function with relative risk aversion ρ, the marginal propensity to consume out of transitory income is[4]

I am satisfied that sensible calibrations of this model involve a relative risk aversion parameter that is greater than or equal to 2, in which case this equation indicates that the income effect is outweighed by the substitution effect so that a decline in interest rates should produce a net decline in spending. This goes in the opposite direction from the human wealth effect, so in principle the model's implications about the effect of interest rates on consumption are ambiguous. In practice, however, as Summers (1981) showed, for essentially all plausible calibrations the perfect foresight model suggests that the human wealth effect should be much larger than the income and substitution effects for most households over most of their lifetimes.
Of course, arbitrary changes in the degree of impatience could explain any pattern of changes in saving rates, and many possible reconfigurations of debt. In order to rule out this possibility, the authors present what I view as among the best measures of this difficult-to-measure quantity: the answers to a survey question from the SCF in which households are asked about their ‘planning horizon’. Lusardi (2003) has recently emphasised the explanatory power of these questions for a wide variety of cross-sectional choices and behaviours. In this particular context, however, the answers to the question do not help much; despite large differences across households in planning horizons, the SCF data suggest that on average households have become, if anything, more rather than less patient (there is a modest increase in the number of households with long planning horizons). Similarly, the proportion of households who admit to planning for retirement has gone up. Thus, it is difficult to make the case that an increase in impatience is responsible for the decline in saving.
The perfect foresight PIH framework has defects as well as virtues for thinking about these questions. Perhaps the most serious limitation is that the model does not predict the existence of any ‘target’ level of net worth. Patient consumers will accumulate unbounded amounts of wealth, while impatient ones will run up their debt to the point where all income is devoted to debt-servicing, and both of these behavioural patterns will take a very long time to work out, far longer than the time frame that is useful for high-frequency macroeconomic analysis.
Fortunately, these problems can be addressed using a modest but powerful extension to the model. All that is necessary is to make the model slightly more realistic in a crucial respect: relax the assumption of perfect certainty. The most transparent way to do this (following Tochè 2005) is to make an extreme assumption; in every period, every employed consumer faces a risk of becoming unemployed, and in the unemployed state income falls to some fraction of its value for an employed consumer (zero, if there is no unemployment insurance; more realistic assumptions can be made at the cost of less tractability). Furthermore, unemployment is an absorbing state: nobody ever emerges from unemployment (and so perhaps retirement is a better interpretation).[5]
This simple modification has profound consequences. Details and derivations are beyond the scope of this discussion; Tochè (2005) treats the problem in continuous time and Carroll (2007) provides a discrete-time version with ample intuition and several examples. The key point, however, is straightforward. The model assumes that consumers are sufficiently impatient that their wealth-to-income ratio would not approach infinity even in a perfect foresight world. The theory then implies the existence of a target level of wealth, because with constant relative risk aversion (CRRA) utility (and imperfectly insurable unemployment risk), the intensity of the precautionary saving motive increases as wealth falls. The target level of net worth will be the point where the degree of prudence exactly matches the degree of impatience.
Rather than working through the model in detail, I will present here only the highlights. The most important of these is the formula for the target level of net worth. Two special cases of the model capture most of the key points. The first is the case where utility is logarithmic (equivalent to ρ = 1). In this case, there will be a target level of net worth of[6]
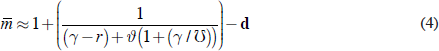
where d is the borrowing limit and γ is the uncertainty-adjusted income growth rate.[7] The effect of the impatience assumptions is to guarantee that the denominator of the fraction is a positive finite number.
This equation neatly collects most of the qualitative, and even some of the quantitative,
predictions of optimisation under uncertainty. For example, an increase in
the time preference rate ϑ will increase the second term in the denominator and so
reduce target net worth 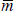 . In contrast with the perfect foresight framework,
however, the model says that the growth rate of consumption is not altered
forever; eventually net worth will approach its new (lower) target level, after
which the growth rate of consumption will again (as before) be equal to the
growth rate of income, and the saving rate will stabilise at a new, lower,
rate.
. In contrast with the perfect foresight framework,
however, the model says that the growth rate of consumption is not altered
forever; eventually net worth will approach its new (lower) target level, after
which the growth rate of consumption will again (as before) be equal to the
growth rate of income, and the saving rate will stabilise at a new, lower,
rate.
The human wealth effects of growth and interest rates are directly captured by the first parenthetical term in the denominator; raise γ or lower r and you will increase the denominator and therefore reduce target wealth.
Again, however, these are effects on the target or steady-state level of m, which is the ratio of net worth to labour income. A change in income growth will have an effect on the target, but in steady state the existence of a target ratio implies that the growth rate of net worth must eventually settle down to the growth rate of income. This is a stark contrast to the implications of the perfect foresight framework in which (in partial equilibrium) wealth levels perpetually rise or fall. (In the perfect foresight model, the growth rate of consumption is unaffected by the growth rate of income; any change in parameters results in a one-time shock to the level of consumption, making it move to the new level from which the new growth rate can be sustained perpetually.) Thus, human wealth effects are (plausibly) more limited in the perfect foresight framework.
In addition to rationalising the role of human wealth and impatience effects, the model captures the effect of uncertainty on target wealth via the γ/Ʊ term. This is most easily understood by considering the consequences of unemployment risk approaching zero; assuming ϑ and γ are both positive, this implies that the denominator will approach infinity, so that the target buffer stock approaches zero. This reflects the fact that so long as there is any positive unemployment risk, the CRRA utility function has the effect of creating a self-imposed borrowing constraint.[8] However, as the risk disappears almost entirely the amount by which target wealth exceeds its minimum possible value becomes arbitrarily small. Conversely, an increase in unemployment risk reduces ϑγ/Ʊ and therefore increases target wealth.
However, the point that deserves perhaps the greatest emphasis, is that the target level of net worth moves one-for-one with movements in the borrowing d. That is, if the borrowing limit increases by $1, then the eventual new equilibrium will be at a point where the extra borrowing capacity has been fully exploited and the consumer's net worth is lower by $1. This suggests that any consumption-smoothing benefits of a relaxation of borrowing constraints will be temporary, lasting only until households have managed to use the new borrowing capacity to adjust their buffer stocks downward.[9]
While there is some debate on the subject, the consensus among labour economists seems to be that there has been a substantial increase in labour income uncertainty in the US over the time frame we are considering. Ceteris paribus, one would have expected an increase in precautionary saving (and an increased reluctance to borrow) as a result. On the other hand, unemployment rates have declined gradually but substantially over the period in question, and the right measure of risk is presumably at the household level rather than the individual level, so it is not entirely clear that the relevant risk levels have increased.
The authors present some interesting evidence on this question based on results from survey questions from the SCF about motivations for saving. Although this question on the survey is somewhat open-ended, the answers tend to be grouped into broad categories, of which the most frequently cited reason is not retirement but liquidity, which a broad-minded person might interpret as reflecting precautionary motives. Interestingly, in accord with their other evidence of a modest increase in credit availability, the need to save for ‘liquidity’ purposes seems to have declined a bit over time. Whether this is a transitory phenomenon on the road to a new equilibrium remains to be seen.
Finally, the paper presents some evidence on whether the degree of risk aversion has changed over time. Because Equation (4) was derived under the assumption of ρ fixed at 1, the role of risk aversion was not apparent. An alternative special case of the model is useful to highlight this effect; assuming r = ϑ and introducing a term η that is increasing in risk aversion, the formula for target wealth is modified to
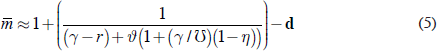
(the difference with Equation (4) is the multiplication of the (γ/Ʊ) term by (1 – η)). Thus, an increase in the intensity of prudence causes a reduction in the denominator and therefore an increase in target wealth.
The data that the authors report do contain some hints that the intensity of precautionary motives may have declined. For example, there is a reduced proportion of households citing liquidity motives for saving, as well as a modest increase in the proportion who say they are willing to take above-average risks to earn above-average returns. Nothing, however, suggests a sea change in risk attitudes of the kind that was entertainingly invoked at the height of the late 1990s share market bubble to argue that shares were (even then!) profoundly undervalued.
Given their systematic dismantling of most alternative explanations for the rise in debt, one senses that the authors suspect that the main explanation for the rise in debt and the fall in saving is the obvious one; financial market innovation made it easier to borrow in the US, and in a world of impatient consumers that means that people have borrowed more.
To explore the implications of that argument, Figures 1–4 depict the dynamics of c, m and c'(m) in response to a one-off increase in the level of the borrowing limit.
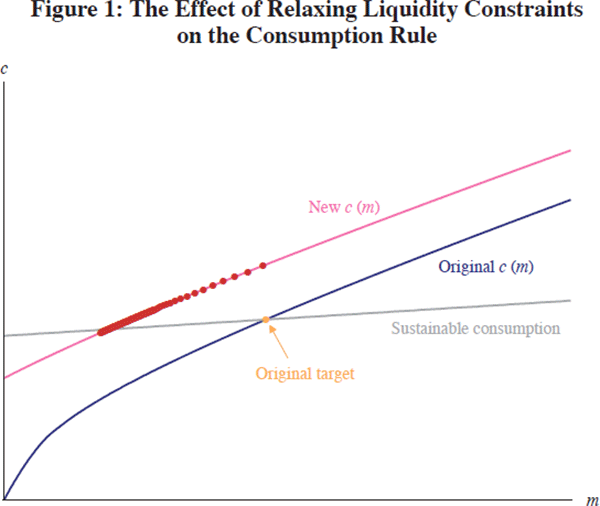
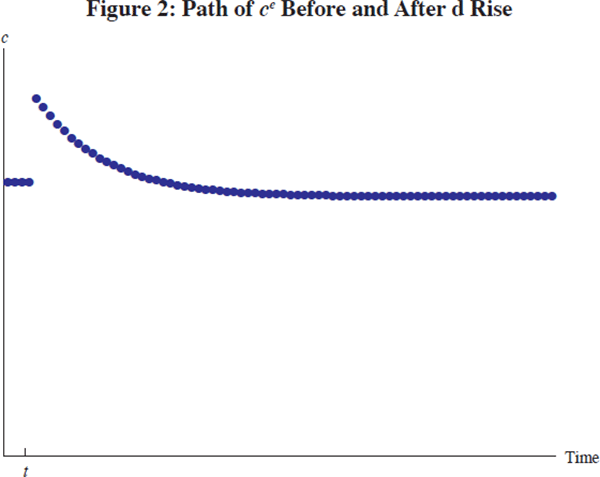
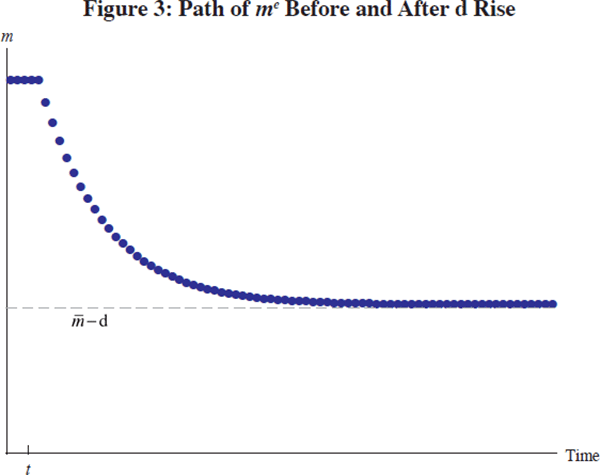
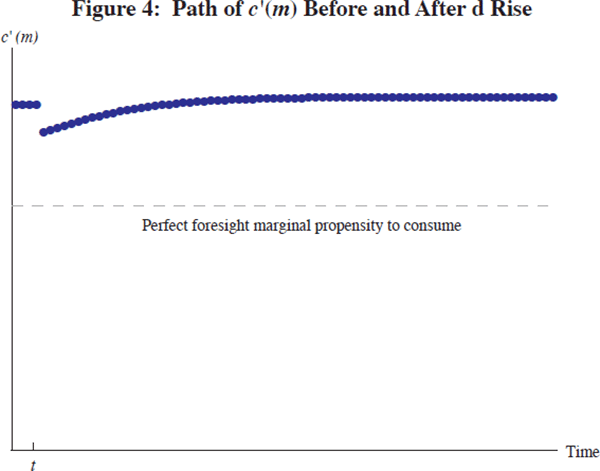
Several features of the results are worth emphasising.
First, the relaxation of the constraint provokes an immediate and large consumption boom as previously constrained consumers go on a spending spree.
Second, however, the ultimate asymptotic destination for the level of consumption is very close to its pre-liberalisation level (the only reason the two are different is that the lower target level of net worth generates a lower equilibrium level of asset income).
Finally, after the initial great leap upward in spending, the transition toward the new equilibrium is quite gradual.[10] From the standpoint of monetary policy and financial stability, it seems safe to conclude that predictable transitional dynamics can reasonably be neglected.
These model results can be turned into a practical interpretation of US macroeconomic history by thinking about the gradual process of financial liberalisation as being like a series of small relaxations in borrowing constraints, each of which individually would have played out in a manner like that indicated in the figures. Under this interpretation, the decline in the saving rate and the increase in debt reflect a large but gradual cumulative relaxation of constraints; gradual enough that there is no single point in time at which an upward spike in consumption like the one depicted in Figure 2 would be evident, but fast enough that the period of adjustment is still ongoing.
A final point about the model is that it implies a high degree of sensitivity of current consumption decisions to households' perceptions of their economic environment. Fortunately for macroeconomic stability, actual spending decisions do not seem to dance on a string to the extent that one might anticipate from the model. The macroeconomic literature presents varying interpretations of the excess smoothness of consumption choices (with habit formation currently occupying a favoured spot), but it seems likely that the key insights of the model would not be undermined by a sensible model that was more realistic in attempting to match the quantitative details of consumption dynamics.
Footnotes
As a finishing point, one might want something closer to the life-cycle model; fortunately, the paper by Kent, Ossolinski and Willard (this volume) provides the complementary set of insights available in that framework. [1]
Lower-case variables reflect the level of the variable normalised by the level of permanent labour income; for example c = C/P. [2]
This is not necessarily inconsistent with aggregate developments, since much of the substantial per-capita income growth over the past 25 years, and especially much of the improvement in growth prospects, has been concentrated at the upper end of the income distribution rather than the median that the authors examine. [3]
In my comments I alternate between the discrete-time and continuous-time solutions to the PIH model, depending on the situation; one of the virtues of the benchmark PIH model is that nothing important depends on the time frame over which the problem is examined. [4]
To permit the examination of human-wealth-preserving spreads in unemployment risk, we need to modify the growth rate of income to be equal to or greater than g so that a change in ‘unemployment risk’ does not change the discounted value of h. [5]
See Carroll (2007) for derivations; the role of debt is an addition for the purposes of this discussion. Labour productivity is assumed to grow by a factor 1 (1−Ʊ). [6]
This will be the ‘natural’ borrowing limit determined by the amount that the consumer could repay in the worst state of the world, namely unemployment starting next period. It will be a function of the unemployment insurance replacement rate, the interest rate and the growth rate. [7]
A consumer who borrowed more than d might be forced to consume zero and would therefore experience negative infinite utility. [8]
This broad point comes through clearly in the much more realistically calibrated simulations in Carroll (2001). [9]
Each dot in the figures represents a year, and the baseline parameterisation was chosen for its ability to generate illustrative figures rather than its realism – a more realistic parameterisation would exhibit even slower transitions. [10]
References
Carroll CD (2001), ‘A Theory of the Consumption Function, With and Without Liquidity Constraints’, Journal of Economic Perspectives, 15(3), pp 23–45. Available at <http://econ.jhu.edu/people/ccarroll/ATheoryv3JEP.pdf>. Expanded version available at <http://econ.jhu.edu/people/ccarroll/ATheoryv3NBER.pdf>. Programs to generate all theoretical results available at <http://econ.jhu.edu/people/ccarroll/ATheoryMath.zip>.
Carroll CD (2007), ‘A Tractable Model of Buffer Stock Saving’, lecture notes/discussion paper, Johns Hopkins University.
Debelle G (2004), ‘Macroeconomic Implications of Rising Household Debt’, BIS Working Papers No 153.
Lusardi A (2003), ‘Planning and Savings for Retirement’, Dartmouth College Working Paper.
Summers LH (1981), ‘Capital Taxation and Accumulation in a Life Cycle Growth Model’, American Economic Review, 71(4), pp 533–544.
Tochè P (2005), ‘A Tractable Model of Precautionary Saving in Continuous Time’, Economics Letters, 87(2), pp 267–272. Available at <http://ideas.repec.org/a/eee/ecolet/v87y2005i2p267-272.html>.