RBA Annual Conference – 1995 Final Discussion

1. Adrian Pagan

Lately, I've been watching television, and one of the people I see on it a lot is Tina Turner. Now Tina may seem to be an odd person to introduce into a central bank conference, but her songs have titles that fit pretty well with some of the issues raised by this Conference. First up, there is the line that she belts out on television in support of the local football code, while standing on what appears to be the Sydney Harbour Bridge: ‘better than all the rest’.

Better Than all the Rest

Ian Castles provided an excellent paper on the difficulties of making inter-country comparisons of living standards, illustrating that a recognition of these difficulties extends back to at least the first decade of this century. He convincingly argued that the ICP results displayed an anti-Australian bias and that multiple-country comparisons should be eschewed in favour of bilateral comparisons, where more reliable assessments could be made. As well as specific issues concerning the valuation of money income, the paper stimulated my thoughts over a few secondary points. In particular, whom should we compare ourselves to and what should be the basis of the comparison? Many times we saw that comparison set as being the OECD average, but I couldn't shake the impression that this was like comparing the Pagan Pastoral Company to BHP. My own preference would be to see comparisons with Canada or Sweden and, in the future, perhaps South Africa, as these represent countries that are of similar population size and/or resource endowments. Related to this aspect is the question of what we want to compare? Much of the Conference was taken up with inter-country comparisons of productivity in sectors such as construction, manufacturing, etc., whereas I felt it might be more useful to look at a traded/non-traded sector division.

Returning to Tina Turner's musical lexicon, outside of the set of rugby league enthusiasts she is probably better known for her chart-toppers, leading me to my second and third themes, which are represented by amended versions of the title of one of her recent hits: ‘what's love got to do with it?’.

What's Supply Got to Do With It?

The Conference was remarkable for the number of ways in which we re-arranged or added to a basic equation. Defining Y, K and L as levels of output, capital and labour respectively, where Y = AK^α L^β is generated by a Cobb-Douglas production function, we can express the growth rates of output, y, capital, k, labour, l, and total-factor productivity, a, as:

from which the growth rate in labour productivity is:

provided constant returns to scale (α + β = 1) are imposed.

Phil Lowe computed the LHS of equation (3) for a variety of industries, making some conjectures about why it was small or negative, particularly in the retailing industry. He then plotted Y/L against the real wage, finding a nice upward-sloping relation. To justify such a connection, we would need to replace (k − l) by the change in the real wage. In periods when the capital stock is fixed, that would be a standard optimality condition, but when k is not fixed, we would expect K/L to depend on the ratio of the wage rate to the rental price of capital, and this may not be proportional to the price level in periods like the late 1980s when real interest rates rose sharply.

Instead of writing the equation as one explaining labour productivity, we could have used it to describe capital-productivity movements:

A comparison of equations (3) and (4) shows that both capital and labour productivity cannot increase without there being an increase in TFP, so that the claims in the Conference of rises in both in recent years is tantamount to a statement about TFP increases.

Table 1 gives estimates of (y – k) for various periods in this country. What is especially noticeable from this table is the weak post-World War II performance in capital productivity, which resulted in a substantial rise in the capital/output ratio. The implication of this is best seen by writing (1) as:

Table 1: Capital Productivity Growth Rates

(Per cent per annum)

1900–10	1.45
1910–29	−1.21
1930–38	2.14
1946–60	−0.75
1961–70	−0.80
1970–79	−0.72
1970–89	0.18
1989–94	0.48
Sources: From 1900–79, the results are from Kaspura and Weldon (1980). For 1970–89 and 1989–94, they are computed, assuming α = 0.3, from OECD Working Paper Nos 145 and 152, respectively.

where I is net investment, an equation Steve Dowrick used in his paper for explaining country variations in growth rates of output. In the post-World War II period Australia attained historically very high investment ratios with gross non-dwelling public investment hovering around 8–10 per cent of GDP, while private investment was in the 10–14 per cent range. But these high shares did not produce particularly high growth rates in output, as the rate of return to capital, 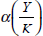, was low. Such a phenomenon was remarked on by Nevile (1967), who concluded that the capital/output ratio in Australia was high by international standards. One might suggest many reasons for this outcome, related to tariff protection, etc, and it is therefore encouraging to see the improvement in capital productivity in the 1990s. Indeed, it is possible that capital productivity has increased at a faster rate than shown in the table. Bob Gordon pointed to the problems of measuring real quantities with deflators that have a fixed base year, and for which there have been sharp changes in quality. Computers are the most obvious offender on this score, and given their importance in Australian equipment investment, Aspden argued that this might be expected to have led to an overstatement of import and investment demand, that is: k.

A different way to use the equation is to define TFP growth:

Michael Sarel performed such an inversion in order to estimate a in Asian economies, concluding that the estimates were sensitive to the size of α (as well as the time period chosen to measure y, l etc). Moreover, some recent revisionist views of the ‘Asian miracle’ could be attributed to their ascribing a large value to α. Writing the equation as above shows that the sensitivity arises only if the capital/output ratio is growing very strongly, and accounts for why growth-accounting exercises performed on industrial economies had not encountered such a problem. Sensitivity of solutions to parameters has also been an issue with computable general equilibrium (CGE) models, and it might be useful to provide sensitivity elasticities 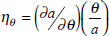of a to a parameter θ, as was done in the CGE context by Pagan and Shannon (1985). Using the numbers in Table 1 of Sarel's paper, η_α = −0.8.

Finally, one might argue that β + α >1, either because of increasing returns in production or because TFP depends on K and L. Starting with a production relation Y = A^* K^γ L^δ and A^* = AK^c L^d, we would have Y = AK^αL^β where α = γ + c, β = δ + d could now easily sum to more than unity. Steve Dowrick dealt with the literature on this way of producing endogenous growth, but very little discussion at the Conference entertained such a possibility. I must admit to being sceptical of the value of this literature, and this perception might have been shared by others.

The idea of focussing upon the supply-side constraint is another useful framework when analysing the possible magnitude of future growth. Capital stock and labour-force growth raise policy issues relating to the savings rate, as well as re-training of the labour force to enhance skills and immigration, and these are best handled by Vince FitzGerald. This leaves the potential growth of TFP to be identified. The National Australia Bank Survey, reported in Oster's paper, has around 2 per cent per annum anticipated productivity growth across most industries for the next three years. The question asked in the survey seems ambiguous. If it was interpreted as labour productivity it would imply a very low rate of TFP growth, so it seems more likely that it is an estimate of a. Hence, one would have to be optimistic about TFP growth.

Growth regression studies provide a decomposition of a into an exogenous component and a ‘catch-up’ term. Steve Dowrick argued that some of the ‘Asian miracle’ could be attributed to the latter, and there was argument at the Conference over how important that explanation was. Results in Sarel's paper tend to suggest that the growth rates of some Asian economies are well explained by growth regressions – see his Table 5 – but the residuals presented in Figure 2 of Helliwell (1991), as well as comments by Ross Garnaut and Wong Fot Chyi, would tend to view such a conclusion as a manifestation of selection bias, with economies such as Hong Kong and Singapore having large positive residuals from growth regressions.

Normally, the expectation would be that an advanced country like Australia would not find much of a contribution from ‘catch-up’ to a. But this stance was belied by the very interesting micro studies that were presented. It seemed as if Australia was well away from best practice in steel production, electricity generation and (possibly) banking, although the gap has been narrowed in the 1990s. These studies suggested that there could be a substantial catch-up contribution to a in the next decade. It would be interesting to see a wider range of studies addressing this possibility.

What's Demand Got to Do With It?

A final issue which surfaced sporadically was the role of demand management in ensuring that y and y^* remained close to one another. It is intriguing to see how demand management has been relegated to a back-seat in discussions of growth. Historically, economists treated demand in its various guises, e.g. trade, as a most important factor in generating growth, as evidenced by the staple theory of growth; Noel Butlin's view that Australian growth was heavily influenced by public investment; and Snooks' (1994) demonstration of fast growth rates in England during 1490 to 1600 (sandwiched between centuries of stagnation).

Andersen and Gruen turned the Conference's attention to demand factors, albeit more on the volatility of the latter rather than its level. I am in general agreement with their main conclusions on the matter of the importance of good demand management, but would quibble with some of the detail. Given my long-standing interest in inflation in Australia, it should be no surprise that the main reservation I had with their paper arose from the work concerning the correlation of inflation and growth. Designating the coefficient of inflation in growth regressions as β, they engage in some ‘meta-analysis’ of past studies regarding the size of β. If we took n independent studies with corresponding estimates of β, 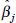(j = 1,...,n), a finding that β is always negative would be extremely strong evidence that the true value of β is negative, since realisations of the random variable 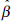show too many from the left-hand tail of its density if β ≥ 0. 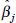But the sampled in Andersen and Gruen's paper are not independent, either due to the ‘extreme-bounds’ technique employed or the use of overlapping time and country observations, and so it is hard to know how significant the finding of a common negative sign is. Although I believe that very large inflation rates are likely to be deleterious for growth, I am not persuaded that the same is true for the range of inflation rates that Andersen and Gruen consider, particularly given the censoring of Iceland and Turkey on the grounds that these moderate growth and high inflation countries weaken the correlation.

References

Helliwell, J. (1991), ‘Conference Summary and Wrap-Up’, in T.J. Courchene and D.D. Purvis (eds), Productivity, Growth and Canada's International Competitiveness, Bell Canada Papers on Economic and Public Policy No. 1, John Deutsch Institute Queen's University, pp. 427–445.

Kaspura, A. and S. Weldon (1980), ‘Productivity Trends in the Australian Economy 1900–01 to 1978–79’, Working Paper No. 9, Department of Productivity Research Branch.

Nevile, J.W. (1967), ‘How Productive is Australian Capital?’, Economic Record, 43(103), pp. 405–411.

Pagan, A.R. and J.H. Shannon (1985), ‘Sensitivity Analysis for Linearized Computable General Equilibrium Models’, in J.R. Piggott and J. Whalley (eds), New Developments in Applied General Equilibrium, Cambridge University Press, Cambridge, pp. 104–118.

Snooks, G.D. (1994), ‘Great Waves of Economic Change: The Industrial Revolution in Historical Perspective 1000 to 2000’, in G.D. Snooks (ed.), Was the Industrial Revolution Necessary?, Routledge, London, pp. 43–78.

2. Vince FitzGerald

Papers at this Conference have ranged from a ‘big picture’ conspectus of growth theories by Steve Dowrick, to several papers canvassing measurement problems – beginning with Ian Castles' – to a series of micro-oriented examinations of productivity performances and their apparent drivers; then back to country and inter-country level growth studies for East and North Asia; and finally to Andersen and Gruen on macroeconomic policies and growth.

I don't intend to try to review all of those contributions. In particular, while I was impressed with what we heard about the sheer fuzziness of our measures of output, and hence price and hence productivity (particularly so in the service sector), I have little further to add on that Conference theme to the discussions we have already had. Equally, it was very valuable to hear from Philip Lowe, Robert Gordon and all of those presenting case studies of comparative productivity levels and productivity growth, but again I don't want to pick up further specific points from those papers, but will reflect on issues discussed in those sessions only at a general level.

I want to focus primarily at the economy-wide and public-policy level, and so mainly on Steve Dowrick's paper and the papers presented by Michael Sarel, Kengo Inoue and Palle Andersen and David Gruen. I myself am very interested in experiences of growth across countries and over time, but my main interest is in policies relevant to Australia here and now, in the 1990s, and over the medium and longer term.

Steve Dowrick's opening paper tabled a summary of the possible explanatory factors for countries' growth experiences (emerging out of his survey of the field), and discussed the policy implications – but this area of policy implications was not, I think, picked up adequately in the subsequent discussion session. His explanatory factors were:

• population growth;
• labour supply;
• physical capital accumulation (equipment and infrastructure particularly);
• human capital;
• knowledge accumulation (as distinct from human capital) – i.e. R&D and the creation of intellectual property;
• government consumption;
• trade and specialisation; and
• macroeconomic settings.

Given time constraints, I have to specialise, so will talk about only this subset of those topics:

• physical capital accumulation;
• government consumption; and
• macroeconomic settings.

That list does not include saving explicitly, but it is closely linked especially to the first item – and also to the other items – on that short list in a number of the papers, and I want to concentrate on it here. (I note that I have written extensively elsewhere on the human capital dimension, specifically on training reform.)^[1]

I have argued elsewhere^[2] that national saving in Australia has recently been sub-optimally low, and seemingly increasingly so from about the mid 1970s onwards. As in a number of other OECD countries, the decline in Australia's saving can largely be attributed to the public sector, and largely at the Federal government level. This attribution is not just a matter of comparisons with the past, but a matter of the fact of persistent public dissaving – i.e. excessive incurrence, on average over the cycle, of debt liabilities to finance recurrent public expenditures. This is something which is not sustainable – either on good public finance principles or in terms of intergenerational equity – and which cannot plausibly be explained away (as some commentators have sought to do) by regarding certain government current spending as capital in nature, at least in part (e.g. education expenditure).^[3] What the decline in national saving has to do with physical (and for that matter, human) capital accumulation and growth I will return to in a moment.

As Andersen and Gruen pointed out at this Conference, Australia has, by comparison with other OECD countries, also seen an unusually large decline in private saving, and clearly so in household saving – noting that saving in enterprises has returned to fairly high levels during the recent (1991–95) recovery. The picture of decline in saving is thus consistent across public and private sectors and in any case does not change radically if alternative measures of saving, counting some human capital related spending as saving, are adopted; moreover, it is not purely cyclical on any measure. I would not argue, even if it could be demonstrated conclusively that policy could raise saving and that this would accelerate growth, that we should necessarily, on that ground alone, do so, if this meant overriding private choices about consumption and saving.

The fundamental public policy reasons for correcting public dissaving I have alluded to already, and there are equivalent arguments for correcting distortions to private saving decisions.^[4] There is also a strong argument – one, I note, which is apparently accepted even by that great New Zealand interventionist Roger Douglas – for requiring minimum self-provision for retirement through private saving earmarked for that purpose, in order to prevent the otherwise very little restricted ability of many present households to impose uncompensated burdens on future taxpaying households. This essentially ‘moral hazard’ argument is especially strong if the proportion of aged in the population is rising rapidly. Note, however, that for a policy for minimum retirement saving to work in intergenerational equity terms, it must succeed in raising the capital intensity of the economy, i.e. capital per worker (and possibly overseas assets per worker) in order to raise the future ratio of non-wage to wage income.

Let me now return to what all these points about saving have to do with growth. Michael Sarel's paper gave an excellent discussion of alternative explanations of the East-Asian growth experience. Especially for Singapore, it would be easy to conclude that his demonstration that Alwyn Young's well-known results are very sensitive to the choice of key parameters throws out the story that Singapore's growth is explained entirely by high rates of provision of factors (and not by total-factor productivity growth). But to conclude this would surely be to ‘throw out the baby with the bath water’. Sarel's figures suggest that even with alternative parameters to those adopted by Young, Singapore's growth is still 60 per cent attributable to causes other than TFP growth, including importantly the high rate of accumulation of capital, financed by high saving rates. In other words, this effect of saving on investment and thence growth may not be the whole story, but it remains standing as a major part of the East-Asian growth story.

While at least some of the East-Asian economies clearly combined this with other important ingredients in growth – including, along the way, relatively high levels and possibly above average rates of accumulation of human capital – there is nevertheless an apparently clear demonstration here that it is possible to raise output per worker by raising capital per worker, whatever rate of TFP growth is being achieved, and to keep doing this over time-scales stretching into decades before this potential source of growth in GDP per capita runs into diminishing returns – as Kengo Inoue's paper indicates may have begun to occur in Japan, although only after many years into the high-growth process.

Of course, saving by definition has a cost in foregone present consumption, and in most macroeconomic models almost any measures to increase it will have the (Keynesian) effect of initially depressing growth below the path it would otherwise take, for perhaps as long as a number of years, before positive effects on investment and productive capacity are reflected in higher GDP growth. Thus we should look at the inter-relationship between saving and growth in an appropriately long time frame.

Andersen and Gruen suggest that, at least to some extent, the well-documented positive association of saving and growth over periods longer than a few years may involve growth stimulating saving rather than the reverse. Sarel also quotes a paper by Carroll and Weil suggesting that it is increased growth which increases saving. It is almost certainly so that higher growth stimulates higher saving, at least as a matter of inertia in spending patterns until there is adjustment to higher levels and growth of incomes, but I do not think that this has been demonstrated to be the main direction of causation. Rather it is likely to be a feedback, and probably a temporary one. Why should households, once they have come to believe that a higher growth rate will be long-lasting – i.e. that they can count on having higher incomes and faster growth in their incomes in the future – react by reducing the proportion of their present low incomes which they consume?

A number of other studies which have examined the causality issue for different countries and over time (e.g. Nelson (1993) and Hutchison (1992)) have shown that the main causality is from saving to investment. Because the effect on investment is less than one for one, the external deficit is also reduced, to a partial extent.

This, indeed, is surely one of the best-established broad empirical facts in economics, thanks to the extensive stream of work started 15 years or so ago by Feldstein and Horioka (1980). Why, particularly when the short-run effect may be to reduce growth, should the main causality be that way, from saving to growth? While the usual attribution of cause is to immobility of capital, I think it is better to think of it as a process whereby increased savings are naturally and rationally more likely to be invested at home than abroad. Here are some plausible reasons for this:

• Given that the main source of decline in OECD saving rates is declining public saving, we can observe that governments in budgetary trouble almost everywhere cut capital expenditure first. In Australia, the consequence of 20 years of this is a clear backlog in many types of infrastructure investment – reflected in the fact that a range of possible ‘catch-up’ infrastructure projects presently show high expected returns. (I have written elsewhere on this.^[5]) By contrast, governments with fundamentally strong budgets can readily borrow on favourable terms to finance good infrastructure, or for that matter, good human capital enhancing expenditures. That is, increased public saving is clearly likely to lead to increased public investment – and, especially if it is achieved via reduced recurrent spending rather than via taxes affecting private incentives to save and invest, to increased national saving and investment, and to a lower underlying external deficit.
• In terms of private saving, one reason for the primary causality being from saving to growth may be as follows. Many of the potential business sector investments, especially in small and middle-sized enterprises (SMEs), can only offer attractive risk/return combinations to well-informed (and necessarily, therefore, mainly local) investors who are or can become familiar with the firms' prospects. Of course, this applies to no investor group more than to the proprietors of such firms (and I believe this is part of the story in some East-Asian countries) which experienced high rates of saving in the form of profits retained in SMEs in the early stages of growth.^[6]

In short, I think that in countries where there is evidence that saving has been sub-optimally low – which seems strongly indicated for Australia, at least – the literature supports the view that policy should and can bring about increased public, and possibly private, saving; and that this will lead to increased capital accumulation and a higher rate of growth over an extended period.

Importantly, there are not many other areas in which we can point to as clear a possibility for government policy to affect growth, but nevertheless this Conference leads me to largely the same kind of conclusions on this score as were reached by both Sarel and Andersen and Gruen – that is, we will at least improve the chances of achieving good growth by maintaining ‘good policies’, including:

• good public finances, namely sustainable (surplus) recurrent budgets;
• good public investments, undertaken (or not) on economic benefit/cost rather than budgetary criteria;
• strong government support for human capital formation, through education and training;
• undistorted incentives for private saving, subject only (on ‘moral hazard’ grounds) to a requirement for minimum self-provision for retirement; and
• generally, stable macro and micro policies conducive to saving and domestic capital accumulation and to productivity growth.

Footnotes

See The Allen Consulting Group (1994a, 1994b). [1]

Principally in FitzGerald (1993). [2]

See FitzGerald (1993, Appendix A). [3]

For an excellent exposition of principles here see Friedman (1990). [4]

See The Allen Consulting Group (1993). [5]

See for example, in respect of Taiwan, Woo and Liu (1993). [6]

References

The Allen Consulting Group (1993), ‘Land Transport Infrastructure: Maximising the Contribution to Economic Growth’, Report to the Australian Automobile Association, November.

The Allen Consulting Group (1994a), ‘Successful Reform: Competitive Skills for Australians and Australian Enterprises’, Report to the Australian National Training Authority, June.

The Allen Consulting Group (1994b), ‘Establishing an Effective Australian Training Market’, Report to the Office of Training and Further Education, Victoria, December.

Feldstein, M. and C. Horioka (1980), ‘Domestic Saving and International Capital Flows’, Economic Journal, 90(June), pp. 314–329.

FitzGerald, V.W. (1993), National Saving: A Report to the Treasurer, Canberra, June.

Friedman, M. (1990), ‘What is the “Right” Amount of Saving’, Policy, 6(3), pp. 52–54.

Hutchison, M.M. (1992), ‘Budget Policy and the Decline of National Saving Revisited’, BIS Economic Papers No. 33, Bank for International Settlements, Basle.

Nelson, E. (1993), ‘Saving, Investment and Government Saving: Asian Evidence’, paper presented to the Conference of Economists, Murdoch University, Western Australia, September.

Woo, W.T. and L.Y. Liu (1993), ‘Investment-Motivated Saving and Current Account Malaise’, paper presented to the Asia Pacific Economic Modelling Conference, Cairns, August.