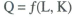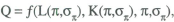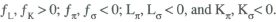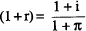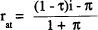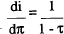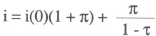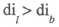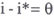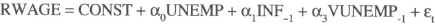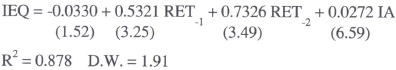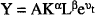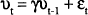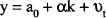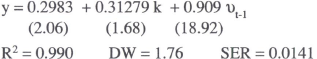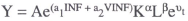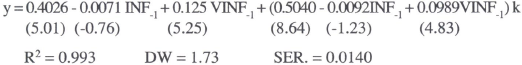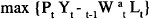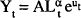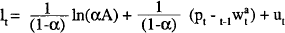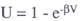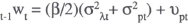RBA Annual Conference – 1992 The Cost of Inflation in Australia Doug McTaggart
‘That inflation is a bad thing and should be eradicated is about as close to a consensus as you are likely to get on any economic or political issue.’ B.W. Fraser, Governor of the Reserve Bank of Australia, 19 April 1990.
1. Introduction
The view of the Governor of the Reserve Bank describes well the common perception of the public's view of inflation. For example, it is not uncommon to hear comments such as (Peter Jonson (1990)):
‘Inflation is theft and an economy built on inflation is one built on deception’
reinforcing the view that the general public ascribes significant costs to inflation. This perception, regarding people's attitude towards inflation, apparently prevails across countries, institutions and cultures. Moreover, as public opinion surveys tend to show, except in times of peak unemployment, the costs of inflation are perceived to be high relative to the costs of unemployment. But, as Fischer and Huizinga (1982) discovered using data provided from American opinion polls, while the polls show that inflation is generally thought to pose a more serious problem than unemployment, the public generally prefers policy directed at reducing unemployment rather than reducing inflation.
The view that inflation creates costs but they are not so large as to outweigh the costs of unemployment created by trying to reduce inflation seems to be predominant among economists, both within and outside the government. Carmichael (1990) goes so far as to suggest that over the 1980s the costs of inflation in Australia were lowered through various reforms and the costs of disinflation remained high so that,
‘…Australia's performance on inflation deteriorated relative to the world trend … [apparently] reflecting a conscious choice within the overall macroeconomic policy strategy of the Government.’
Thus, in some respects, inflation is rather like Mark Twain's description of the weather: something everybody talks about but nobody does anything about. However, unlike the weather over which policy makers have very little control, the average rate of inflation is ultimately a choice variable. So the puzzle is to explain why perceptions of inflation are so negative and yet, at the same time, there is very little imperative to actually tackle the problem head on.
One resolution of the puzzle might follow because, in contrast to unemployment where its costs are concentrated on a relatively small, identifiable, segment of the population and are clearly visible, the costs of inflation are more nebulous and are dispersed over the entire population. A clear constituency for reducing unemployment develops, but not so in the case of inflation. In contrast, in countries such as Germany, where a broad-based collective memory of the effects of hyperinflation is still relatively strong, policy leans towards being anti-inflationary. In countries such as Canada, where in recent years a strong case has been made that inflation imposes significant and measurable social costs, a ‘zero inflation target’ has gained strong support within the ranks of Canada's monetary authorities.[1]
Nevertheless it would appear that pro-deflationary stances are the exception rather than the rule. One reason for this is the apparent difficulty economists have had in quantifying the costs of inflation within a broadly accepted framework. While there has been no shortage of survey articles cataloguing a bewildering array of costs attributable to inflation, the common conclusion is that the actual size of these costs is impossible to quantify. Where empirical studies have been attempted, the results are often subject to more than the usual degree of reinterpretation associated with empirical work.
It is against this background that this paper attempts to analyse the costs of inflation as they pertain to Australia. Section 2 surveys the literature and catalogues the array of costs generally thought to be associated with inflation and its variability. These various components of the costs of inflation are then set in a simple but general framework wherein any real costs associated with inflation must, one way or another, derive from behaviour where one or more of the fundamental inputs into the aggregate supply equation, or production function, has been adversely effected. That is, to have an adverse effect on real output, inflation must reduce either the capital stock or the labour force. Or inflation must induce a reallocation of resources such that, for given quantities of capital and labour, production techniques are modified so that the stocks of inputs are used less effectively.
Section 3 considers the relationship between the level of inflation and some measure of its variability. Since uncertainty about the inflation rate is generally raised as an important determinant for some economic decisions, we discuss the connection that both the level and variability of inflation have with uncertainty.
In Section 4 we consider the effects of inflation on interest rates and exchange rates. The objective here is to ascertain the extent to which inflation distorts price signals received by savers and investors, on the one hand, and the traded and non-traded sectors, on the other hand. If inflation, or uncertainty about inflation, alters these relative prices, then resources will be put to uses in an inflationary world that they would not be put to if inflation was zero.
A very large literature has accumulated wherein economists have looked at the effects of inflation on key prices. Less interest appears to have been devoted to ascertaining the effects of inflation on actual quantities of labour, capital and output. If inflation has any costs then it will have an impact on aggregate output only if it in some way affects the inputs into the production process. Section 5 reviews the effects of inflation on the capital stock and the level of employment. Following from this discussion, Section 6 reviews the aggregate effects of inflation on output. Conclusions follow in the last section.
2. An Overview
(a) Previous Surveys of the Costs of Inflation
The first significant contribution to the costs of inflation literature was Bailey (1956), wherein he measured the welfare losses associated with inflation as consumer surplus lost when anticipated inflation is reflected in nominal interest rates, and money holders substitute increased transactions for lower real money balances. In other words inflation induces ‘shoe leather’ costs.
Following this, Okun (1971, 1975) sketched a model of how inflation interferes with the normal operation of customer markets. These are markets in which information is costly, and decision rules reflect this. Consumers, job seekers and others economise on resources devoted to transacting in customer markets by using simple rules of thumb and forming habits. Because inflation adds noise to price signals, it distorts these simple rules and habits. For example, consumers are forced to search and shop more often. They are forced to compile more information and to try and predict the future – which Okun claims they are poorly qualified to do, and thus their level of anxiety rises.[2]
From these two approaches a substantial literature on the costs of inflation developed. Useful surveys of this literature can be found in Laidler and Parkin (1975), Fischer and Modigliani (1978), Fischer (1981a,1984), Driffill, Mizon and Ulph (1990), and Howitt (1990). Carmichael (1990) provides a brief survey in his discussion of inflation in Australia, and Jonson (1990) offers a non-technical survey. The most comprehensive and structural account of the effects of inflation in Australia can be found in a collection of conference papers edited by Pagan and Trivedi (1983).
Without exception, these surveys catalogue a wide variety of costs associated with inflation, but all conclude that while real costs almost certainly exist they are either too small to worry about, or they are too difficult to quantify.
A related literature, developed more or less independently of the costs of inflation literature, is concerned with the short- and long-run impacts of inflation on output. Two recent contributions are Andersen (1989) and Orphanides and Solow (1990).[3] Since these papers are generally interested in identifying short-run and long-run Phillips curves, they highlight a fundamental difficulty for studies of the costs of inflation, because they begin with the proposition that inflation and output may be positively correlated in the short-run, and possibly the long-run. They then go on to explain why and to identify the robustness of their initial proposition. In contradistinction, evaluating the costs of inflation in any meaningful sense requires one to begin with the proposition that inflation and output are negatively correlated, certainly in the long-run, and possibly even in the short-run. Thus, there would appear to be a significant clash of literatures.
(b) Simple Taxonomies
The natural starting point for considering the costs of inflation is to begin with a world in which inflation has no costs. Pagan and Trivedi (1983) put it in the following way:
‘Suppose all inflation is perfectly anticipated, that it is uniform, all agents have demand and supply functions not exhibiting money illusion, and that there is no uncertainty, distortionary taxes, or costs of price changes.’
Add in the assumption that there are no other nominal rigidities, then all relative prices remain constant and inflation has no real effects. In Howitt's jargon (Howitt (1990)), such a world exhibits ‘inflation neutrality’. Any deviation from the ideal world will result in inflation being non-neutral, or having real effects, which fall into one of three categories:
- direct effects on efficiency;
- direct equity or distributional effects; and
- indirect effects on efficiency resulting from directly unproductive activities, as people attempt to avoid the distributional effects of inflation.
(i) Efficiency Effects
Shoe-leather costs of inflation are usually raised as an important real effect. As Howitt notes, these costs include both the private costs of increased transactions (Bailey (1956) and Friedman(1969)) and the social costs of holding suboptimal amounts of the public good money (Laidler (1978)). However, by almost all accounts, this cost measured as the familiar Harberger triangle is small. Using plausible figures in a back-of-the-envelope calculation, Carmichael (1990) estimates that reducing inflation from 8 per cent to 7 per cent would induce a welfare gain in Australia of around $2 million in 1990 dollars, or about 0.0005 per cent of GDP.[4]
More pervasive than the shoe-leather costs are what Cozier and Selody (1992) call the menu costs of inflation. Their use of the terminology expands its definition, from the common use of referring to the resource costs of changing prices (Sheshinski and Weiss (1977), Parkin (1986)), to cover any direct effect inflation has on the functioning of the price system. Included are the deadweight losses from uncoordinated price adjustments (Leijonhufvud (1980)), the efficiency losses arising from resource misallocations as the distinction between relative and absolute prices becomes blurred (Lucas (1973)), the efficiency loss from increased product standardisation (Carlton (1982)), deadweight losses from increased relative price dispersion (Parks(1978)), and increased search costs (Paroush (1986)).
Inflation also interacts with the wage and tax system, pushing wage-earners into higher tax brackets (bracket creep) inducing labour/leisure substitutions, and it necessitates more frequent wage negotiations, increasing the probability of industrial unrest (Siebert and Addison (1981)).
With respect to capital, inflation has direct efficiency effects through its interaction with the tax system because of the way income is measured for taxation purposes (Vann and Dixon (1990)). Inflation increases the effective tax rate on profits because it reduces the real value of depreciation allowances when nominally fixed historical cost accounting methods are used, and because of the common use of first-in-first-out inventory accounting systems (stock valuation problems). It reduces the benefits of businesses carrying forward nominal losses. On the other hand, the deductibility of nominal tax payments for business borrowers increases the benefits of debt financing as opposed to equity financing. But the taxation of nominal interest income may effectively reduce the incentive to save, thus effecting the supply of loanable funds from which investment is financed. These issues have created an immense literature. Important contributions have been made by Feldstein (1976, 1982) and Feldstein and Slemrod (1978). Nowotny (1980) and Feldstein (1983) provide comprehensive surveys. Recent treatments of the Australian experience can be found in Pagan and Trivedi (1983), Ryan (1990) and Freebairn (1991).
Inflation might not only have effects on the aggregate capital stock, but it might affect the mix of the domestic capital stock in two ways. Because the above mentioned distortions vary across industries, the incentives to invest in and hold different types of physical capital will be affected (Freebairn (1991)). Kent and Scott (1991) discuss the cross-sectional variations in investment patterns over the latter half of the 1980s, some of which may be attributed to inflation. Distortions might also be introduced concerning the vintage of the capital stock. Since inflation erodes the real value of investment and depreciation allowances, the incentive created is to invest in shorter-lived capital and to eschew large scale, longer-term projects.
On top of these distributional effects relating to cross-sectoral investment patterns, the interaction between market structures and menu costs might significantly affect relative price structures across industries and thus the sectoral distribution of profits. Esposito and Esposito (1976) find that a firm's pricing policy varies according to the market structure in which it operates. Firms less able to ‘pass-on’ cost increases suffer from significantly larger profit decreases during inflationary periods. Since profitability directly affects the incentive to invest, disruptions to the distributions of profits which would not have occurred in the absence of inflation will further add to the distortion of cross-sectoral investment patterns.
So too will rigidities or other distortions which interrupt the processes restoring purchasing power parity conditions following an increase in the domestic price level. To the extent that the nominal exchange rate does not adjust to maintain constancy of the real exchange rate, domestic inflation ultimately reduces domestic competitiveness on world markets. This will be reflected in declining profitability in the traded goods sector, and a movement of resources out of the traded goods sector into the non-traded goods sector – a movement that would not have occurred in the absence of inflation.
(ii) Distributional Effects
Cassidy (1991) discusses the distributional implications of inflation, and their significance for Australia. He notes that inflation can have redistributive effects on income, outlays and wealth. With respect to income, it is often suggested that there will be a transfer from creditors to debtors as a result of inflation. But this can only occur if inflation is typically less than anticipated. Otherwise the transfers go in the other direction. And to the extent that inflation is, on average, correctly anticipated, then nominal interest rates may adjust to reflect this.[5]
Second, both anticipated and unanticipated inflation will transfer income away from people on fixed incomes of one type or another – for example, pensions and other superannuation payments.
With respect to outlays, a non-uniform inflation could differentially affect different income groups because of differing consumption patterns. If, for example, the average price of necessities rose faster than the aggregate price index, it would disadvantage those groups who consume a proportionately larger fraction of necessities in the consumption bundle. It is often asserted that lower income groups are in this position. Cassidy (1991), while reporting mixed results from the overseas literature, can find little effect in Australia.
The interaction between inflation and the nominally fixed personal income tax scales leads to a redistribution of income, and hence purchasing power, away from households towards the government as a result of ‘bracket creep’ or ‘fiscal drag’.[6] However, as Carmichael (1990) and Cassidy (1991) note, over the 1980s these effects have been largely offset by periodic adjustments to the tax scales.
Another redistributive effect follows from the non-indexation of payment schedules on loans, particularly housing loans. This leads to a ‘front-end loading’, on mortgages.[7] That is, the schedule of loan repayments is such that real loan repayments are higher in the first years of a loan and then gradually decline. In addition, because housing loan interest costs are not deductible, and because nominal housing loan rates might rise in excess of the rate inflation due to the tax-adjusted Fisher effect (see below), then the costs of housing loan service rises initially, potentially reducing the affordability of housing for lower income groups.
Not only does inflation redistribute income, it also redistributes wealth. To the extent that wealth holders do not or cannot fully insulate their portfolios of nominally denominated assets, inflation further shifts purchasing power through the ‘inflation tax’ as it erodes the real value of nominally denominated assets. For example, Cassidy (1991) notes that during 1989/90 roughly $12.2 billion in notes and coin were held by the public. With an average inflation rate of around 7 per cent, the inflation tax netted the government roughly $900 million. Over the 1980s inflation tax revenues from notes and coins amounted to around $6 billion. Further transfers occur between different sectors of the private economy whenever fixed-interest nominal debt instruments are traded. Cheque accounts and certain government securities fall into this category, as do equities.
(iii) Redistributions and Efficiency
That inflation, by itself, causes income and/or wealth redistributions does not imply that it inflicts costs on society, except in the case that such redistributions are contrary to the overall thrust of public policy, increasing the probability of other offsetting policy action which increases overall uncertainty about future policy. Rather, inflation-induced redistributions are costly because they induce changes in behaviour, as individuals reallocate resources so as to avoid the effects of inflation or to take advantage of such redistributions. That is, time and resources are diverted away from their initial use into directly unproductive activities in an attempt to change the distribution of income. While references to the ‘financially astute’ enriching themselves at the expense of others conjures up an image of ‘unfairness’, because they are more able to rearrange their affairs to benefit from inflation, or at least to minimise the costs on themselves (B .W. Fraser (1991)), this unequal distribution of opportunity cannot be considered a cost of inflation. Instead, it is because resources are being used in activities in which they would not otherwise be used, except for the existence of inflation, that efficiency losses are incurred. It is in this regard that ‘inflation is theft’ (Jonson (1991)) because, just as command over one's own resources is jeopardised in a world where property rights are not respected and individuals thus devote resources to fighting crime, so inflation jeopardises the real value of one's income and assets and, again, real resources are devoted to actions intended to protect them.
(c) Institutional Rigidities
As we have noted, it is generally accepted that inflation would not impose any costs if there were no institutional or other nominal rigidities. This is the organising principle adopted by Fischer and Modigliani (1978), and Fischer (1981a, 1984) in comprehensive surveys of the costs of inflation. However, even in a fully indexed economy costs of inflation would arise because interest is not paid on currency (nominal returns on currency are fixed at zero) and marked prices on goods would still need to be changed continuously, absorbing real resources (narrowly defined ‘menu costs’). So, contrary to popular assertion, the comprehensive use of indexing arrangements would not mitigate all the costs of inflation.[8] But apart from these shoe-leather and menu costs, all the remaining costs of inflation result from nominal rigidities of either public or private institutions.
Public institution rigidities refer mainly to the progressive taxation of nominal incomes, with non-indexed tax scales. In addition, the government uses nominally-based accounting methods. One implication of the latter is the overstatement of government deficits in inflationary periods (Makin (1990), for example) and this, by itself, may have implications for the conduct of future fiscal policy (see Eisner (1989)). For example, it can reasonably be claimed that the complete overhaul of the financial and monetary management systems in Australia since the mid-1970s was official action taken to counteract the financial markets' responses to inflation in a world with serious nominal rigidities – fixed nominal interest rates, to name just one. Inflation has thus had an immense impact on these public and private institutions and has brought about costly adaptations. This adaptive process continues, possibly indicating continuing costs of inflation.
Other rigid private institutions include the continued reliance on nominal contracts, mortgages in particular, and the use of nominal accounting methods in business.
However we taxonomise the costs of inflation, there seems little dispute that such costs exist, and that the variety is large. What is not clear, however, is the extent to which the costs are large enough to warrant remedy, other than to adapt rigid institutions further. This ambiguity arises in part because of the difficulties inherent in empirical work attempting to measure the costs. We now turn to this issue.
(d) Measuring the Costs of Inflation
It is not simply enough to assert that inflation has costs insofar as the allocation of resources is different in a world with inflation from what it would be in a world without inflation. For this proposition to be valid, it must also be true that there are no externalities in the economic system which are effectively internalised by some inflation. This, after all, was the reasoning underlying attempts to justify policy directed at exploiting inflation-unemployment tradeoffs, manifest in positively sloped and short- or long-run Phillips curves.
Figure 1 portrays the situation. The aggregate demand curve, denoted AD, is downward sloping for the usual reasons – primarily intertemporal and international substitution effects. The short-run aggregate supply curve, SAS, has a positive slope, compatible with a downward-sloping short-run Phillips curve. The positive slope of the SAS curve is the result either of nominal rigidities (fixed nominal wage contracts, Fischer (1977), for example) or the result of costly information and inflation variability ((Lucas (1973), for example). The long-run aggregate supply curve, LAS, is vertical, its position determined by the economy's stock of productive resources and technology. In the absence of macroeconomic externalities, Q0, the level of output determined by the LAS curve, represents output in an inflation neutral world.[9]
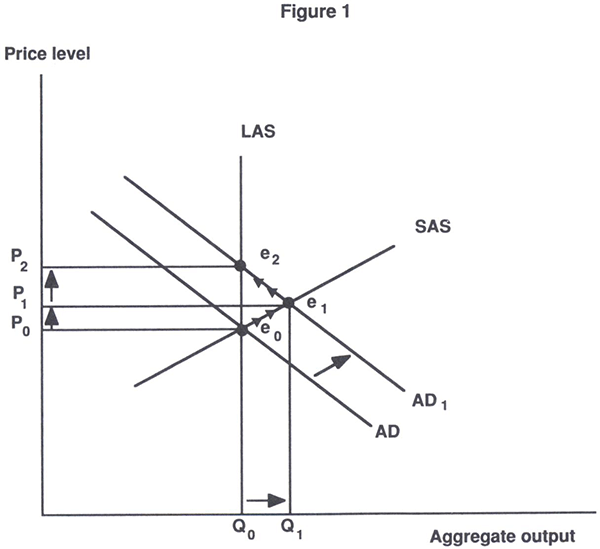
Supposing we believed that the long-run or inflation-neutral level of output, Q0, was suboptimal, then we might be induced to expand the money supply, or adopt some other policy, to shift the AD curve rightward. Short-run equilibrium moves from e0 to e1, with output and prices rising. As long as prices did not instantaneously adjust, we would observe a positive correlation between inflation and output. In this instance, inflation has conferred benefits on the economy, by exploiting institutional rigidities or costly information to internalise whatever externality was in existence.
If, for whatever reason, the movement to e1 was only temporary and the economy eventually adjusted shifting from e1 to e2 (as the SAS shifted upwards) then we would observe a period where output and inflation were negatively correlated. But we would not want to ascribe the reduction in output associated with this inflation as a ‘cost’. It is a cost that should be attributed to the existence of the externality which is causing the inflation-neutral level of output to be below the optimal level.[10]
However, if it was the case that Q0 was in fact optimal, moving from e0 to e1 would represent a cost. This cost arises because individuals are induced into actions they would not have undertaken in the absence of inflation. But in this case, the costs are related to increasing output (and prices), while the subsequent reduction in output as the economy re-establishes long-run equilibrium should be interpreted as a mitigation of those costs. In other words, in this case we would be looking costs associated with positive correlations between output and prices (inflation).
The important message from the above discussion is that any measure of the costs of inflation will critically depend on one's view of the appropriate functioning of the economy. In this regard, costs measures will be highly subjective. We might expect that economists with a Keynesian bias would find fewer costs attributable to inflation than would economists with a monetarist or neoclassical bias.
A second difficulty exists because inflation arises for reasons other than inappropriate policy. Presumably, we are concerned with inflation being costly so as to guide policy choices. That is, if inflation is costly and the result of particular demand management policies, then it might be desirable to remove the costs by amending policy. But if the AD curve shifts around because of other exogenous disturbances, then we might not want to be changing policy on account of exogenously induced inflation.
Third, inflation often results from significant supply-side disturbances. If following some real shock the SAS curve shifts upward, as shown in Figure 2, and the economy moves from e0 to e1, output falls while prices rise. Again, assuming that prices do not instantaneously adjust, we would observe a period where inflation and output were negatively correlated.
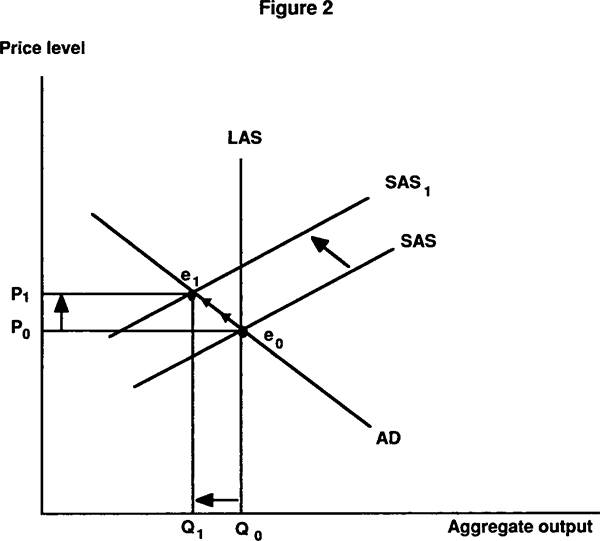
Once again the fall in output is the result of the institutional factors giving the SAS curve a positive slope. If these rigidities did not exist then prices would adjust immediately, with no change in output. Thus it would be incorrect to impute a cost to inflation, as is often done, on the grounds that output and inflation might, for some period of time, be negatively correlated. This confounding of cyclical supply side and exogenous (with respect to policy) demand side shocks makes the task of identifying in the data the costs of inflation very difficult.
The true costs we are trying to measure are shown in Figure 3, in which both the AD and SAS curves are shifting upward as a result of a policy-induced inflation. That the adjustment from e0 to e1 might lead to output variability is a complication that will for now be ignored. In an inflation-neutral world, the adjustment to the policy-induced inflation would be such that Q0 is unaffected. But if the array of institutional rigidities catalogued above exists, it seems likely that resources will be reallocated such that the maximum available output given these resources declines. That is, one of the following will occur:
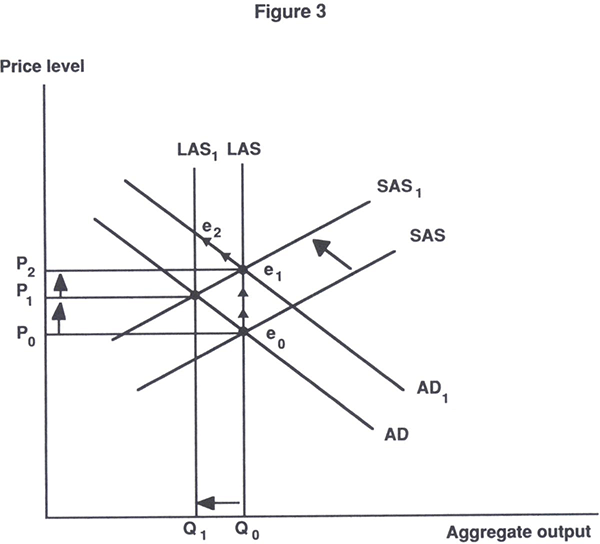
- the level of effective capital stock will be lower; and/or
- the effective labour force will be lower; and/or
- the way effective labour and capital is combined will change, so that Q0 falls to Q1 – the long-run supply curve shifts to the left.
Thus, the difficult task facing the econometrician is to identify changes in the long-run supply curve from all the other effects on measured output. This task has proved sufficiently difficult that the case that inflation imposes significant costs on the economy apparently has not been convincingly made.
Recent attempts to estimate the costs of inflation have begun with particular parameterisations of long-run output. In its most general specification, the level of output in an inflation-neutral world is:
where K is the effective capital stock, L the effective labour supply and technology is embedded in the function f. If inflation has costs, and these are reflected in resource allocations that would not exist in a world with no inflation, then long-run output can be expressed:
where
The various rigidities, structural non-adaptations and directly unproductive activities discussed above are all manifest in the negative first partial derivatives. Empirical work, if it is to be convincing, must begin with something like the above.
To summarise, the difficulty faced when investigating the costs of inflation is that we are looking for deviations of the level of output from a measure of potential output that would exist in an inflation-neutral world and which are the result of correctible policy choices. In principle, in the absence of other macroeconomic externalities, any deviations from the inflation-neutral level of output, positive or negative, which derive from policy decisions incur a cost that could potentially be eliminated by appropriate policy. But because inflation results from many factors other than policy choices, and because output is also endogenously determined by a host of other factors, a significant identification problem pervades empirical work on the costs of inflation.
3. Inflation: Levels, Variability and Uncertainty
(a) Inflation Levels
Apart from the effects on inflation of the recent recession, Australia's experience with inflation over the last two decades is well documented in Carmichael (1990). Further evidence is provided by Figures 4 and 5. Figure 4 shows the inflation rate, calculated as the percentage quarterly change in both the Consumer Price Index (CPI) and the GDP deflator. Although the public perception of inflation usually is concerned with changes in the CPI, both measures were constructed and used in subsequent empirical work to confront criticisms that various ‘fiddles’ in the official construction of the CPI have significant effects. A prominent example is the so-called Medibank fiddle in the first quarter of 1984, an adjustment made to account for changes in the national health care scheme.
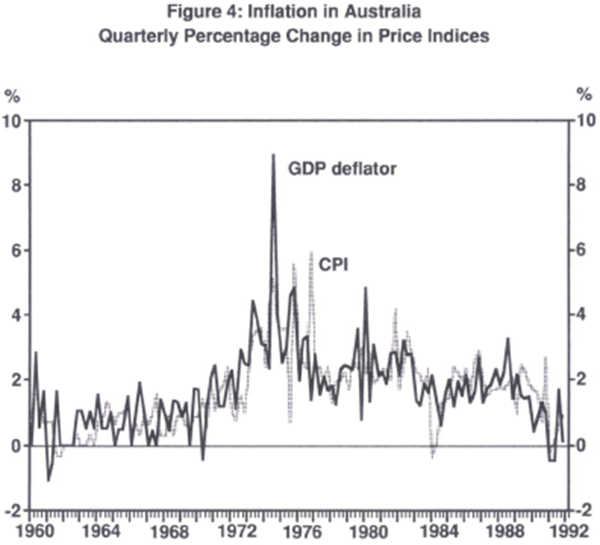
The behaviour of both series indicates that Australia lived with relatively low inflation during the 1960s. Inflation rose rapidly in the early 1970s, as did its apparent variability, although we will discuss that below. From 1975 on it appears that Australia struggled to bring the average level of inflation down. Most recently, inflation has fallen significantly under the influence of the 1990–91 recession. Whether or not these lower inflation rates are permanent remains to be seen.
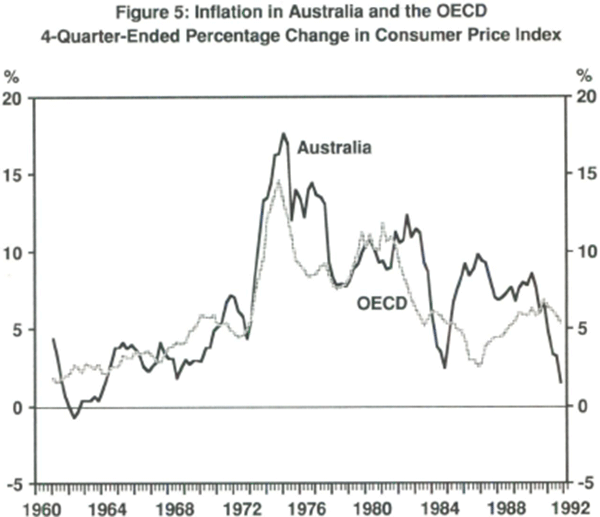
Figure 5 shows Australia's performance with inflation relative to its major trading partners. In this figure the inflation rate, both for Australia and the OECD, is calculated as the four quarter change in the respective CPIs. Overall, Australia performed about as well, or badly, as did the OECD on average with respect to inflation during the 1960s and 1970s. Over the 1980s, Australia's inflation rate was significantly higher, although currently Australia's inflation rate is significantly lower.
(b) Variability and Uncertainty
(i) Inflation and Variability
A considerable literature has accumulated concerning the relationship between the level of inflation and its variability. The hypothesis often advanced is that the higher the average rate of inflation, the greater is its variability. The implication of this hypothesis is that greater variability is associated with increased uncertainty, and uncertainty about inflation generates costs over and above what would emerge in a world with less uncertainty.
Okun (1971) first suggested that the level of inflation and its variability were positively related. Early attempts to test this hypothesis include Logue and Willet (1976), Foster (1978) and Cukierman and Wachtel (1981) and, generally speaking, the data confirmed the Okun hypothesis. Taylor (1981) confirms the results using both time series and international cross sectional data.
A related literature concerns the relationship between inflation and the variability of relative prices. Once again the hypothesis put forward is that the variability of relative prices is positively related to the average level of inflation. Vining and Eltertowski (1976), Parks (1978), Fischer (1981b), Domberger (1987), and Hartman (1991) have contributed to this literature.
A relationship between relative price variability and inflation seems easier to justify on theoretical grounds than does a relationship between inflation and its own variability. In the former case, as the average level of inflation rises and individuals are required to change individual prices more often, the existence of menu costs will mean that such decisions become increasingly uncoordinated and some measure of the dispersion of relative prices will increase. As relative price differentials increase, it may become harder for individuals to discern relative price changes from aggregate price level changes and the process compounds.
However, there does not seem to be any reason to assume a connection going back in the other direction. That is, there is not an obvious reason why the aggregate or average price level should increase simply because the variability of its component parts does. Thus explanations of the link between inflation and its variability usually take a different tack. One line of argument suggests that trend inflation is less stable when it is high. This may occur because high inflation is more likely to bring about a policy response which will reduce it. Thus high inflation causes uncertainty about disinflation (Ball (1990)), or whether or not trend inflation will fall. Other explanations rely on exogenous changes in trend inflation increasing the variability of inflation. Ball and Cecchetti (1990) briefly review these models.
Cukierman and Meltzer (1986) formulate a model wherein the output effects of monetary surprises induce the monetary authorities to create a positive trend inflation. This is the familiar outcome of game theoretic approaches to monetary policy. In Cukierman and Meltzer's model, an exogenous increase in monetary control errors increases uncertainty about inflation, which increases the effectiveness of monetary surprises. This induces the monetary authority to increase trend inflation, generating a positive correlation between the variability of inflation and its trend.
In our discussion of inflation and the labour market below, we sketch a model of wage contracting with risk averse workers wherein, with an accommodating monetary policy, an increase in the variability of inflation will induce an increase in the average level of inflation.
(ii) Output and Uncertainty
Accepting for now that increased variability is accompanied by increased uncertainty, a number of arguments have been put forward explaining why this might involve real costs. The most commonly attributed cost arises because producers operating in an inflationary environment receive distorted price signals concerning demand for their own product. This arises both because of increased relative price variability, and also because of increased aggregate/relative price confusion (see Cukierman (1984)). If such distortions are persistent, then resource allocations will be different in an inflationary economy as compared with a non-inflationary economy. In particular, investment patterns will be disrupted.
A related consequence of increased uncertainty is that different savers and investors in the bond market form different expectations of inflation and hence hold different perceptions of the ex ante real rate of interest. As a result, rates of return on investments are not equalised at the margin, causing a further misallocation of capital (Cukierman (1978)).
As a general principle, increased uncertainty about the value of future income and consumption streams will, for well understood reasons, induce substitutions into the less risky assets. That is, increased uncertainty about future prices will shorten the time horizons over which decisions are made. A practical implication of this behaviour would be a substitution out of consumption of future goods (reduced current saving) into increased current consumption. The pool of loanable funds dries up and the cost of investment rises. And investment patterns might be distorted away from projects with long lives to projects with much shorter horizons and pay-back periods.
Increased uncertainty will reduce the utility of long-term contracts, leading to shorter average contract lengths, and concomitant increased transactions and negotiations costs (Siebert and Addison (1981)). Moreover, it will lead to increased product standardisation and a reduced range of choice compared to what would have prevailed in a world with less uncertainty (Carlton (1982)).
The empirical literature tends to confirm the negative association between real output growth and the variability of inflation. This literature includes Blejer and Liederman (1980), Levi and Makin (1980), Mullineaux (1980), Logue and Sweeney (1981), and Makin (1983). However a persistent concern about these results is the distinction between variability and uncertainty, to which we now turn.
(iii) Inflation Variability and Uncertainty
A common approach in the early literature on the effects of uncertainty on output was to equate some measure of the variability of inflation with uncertainty regarding its behaviour. Okun (1971), for example, uses correlations between the mean rate of inflation and its standard deviation in a multi-country sample to demonstrate the positive relationship between the level of inflation and its variability. But it is now widely understood that variability and uncertainty are not the same thing. Inflation might be highly variable, but if the processes generating the variability are understood there might be little associated uncertainty. On the other hand, inflation might exhibit little variability but be associated with a large amount of uncertainty. This proposition is consistent with the proposition underlying the Ball (1990) model, where high average but stable rates of inflation increase uncertainty regarding future policy responses.
The distinction between variability and uncertainty thus hinges on the difference between the unconditional and the conditional variance of inflation. In this formulation, uncertainty increases only if the conditional variance of inflation rises (equivalently, the variance of unanticipated inflation), given some predefined conditioning set. Engle (1983) recognised this problem and, using his ARCH framework wherein the variance of inflation is allowed to be a known stationary stochastic process dependent on previous forecast errors, he showed that there was no relationship in the U.S. data between the variability of inflation and uncertainty. Subsequent extensions of the ARCH methodology have confirmed this finding.
A significant paper by Pagan, Hall and Trivedi (1983) provides a unifying theoretical framework for discussions of inflation variability and uncertainty. They go on to provide rigorous definitions of uncertainty, and elaborate on appropriate econometric methods for identifying uncertainty in the data. Their methods are related to Engle's ARCH methodology in that they use regression techniques to parameterise the anticipated and unanticipated components of inflation, and they identify uncertainty with heteroscedastic error processes.
ARCH and related models have been estimated on the basis that the structure of the inflation process has remained constant over the sample period. Based on this assumption, the time varying conditional variance is estimated using the entire sample. But it is unlikely that, over any period of reasonable length, the structure of the inflation process has not changed. Such changes may well result from announced, fully-anticipated and believed changes in monetary policy. To overcome this problem, Evans (1991) estimates a simple ARCH error process in a model with time varying parameters for the inflation process. With the aid of a Kalman Filter methodology, and using only historically available data, Evans recomputes a measure of the conditional variance. His results partly confirm Engle's, in that there appears to be little connection between the average level of inflation and uncertainty in the short-term but, in contrast, Evans finds there appears to be a strong positive relationship between uncertainty and average inflation in the long-run.
This distinction between short-run and long-run uncertainty had been investigated by Ball and Cecchetti (1990), in the context of an unobserved components model. They conclude, in line with Evans, that a rise in the level of inflation has little effect on the variance of deviations, but has a considerable effect on the trend. Their interpretation of this is that the level of inflation has little effect on short-term uncertainty, but has a big effect on long-term uncertainty.
Turning to Australian data, Parkinson (1991) replicates Ball and Cecchetti's methods and arrives at similar conclusions. Pagan, Hall and Trivedi (1983) also find a significant positive relationship between the level of inflation and uncertainty in the Australian data.
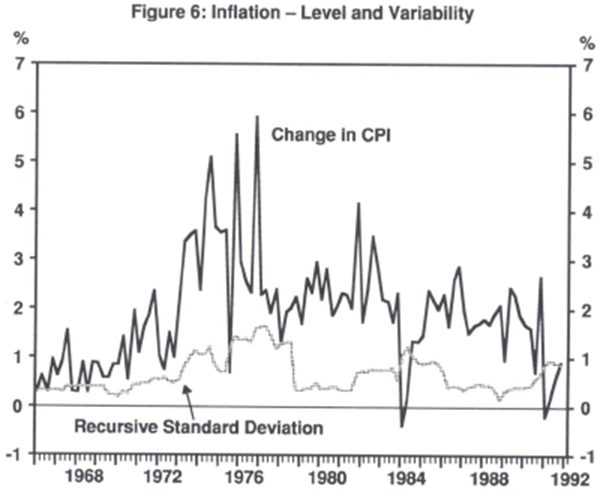
Figures 6 and 7 provide some crude graphical evidence of these relationships. Figure 6 shows the relationship between the level of inflation and its variability. Here variability is measured as an eighth order recursive standard deviation. Since the data are quarterly, it represents a rolling two-year standard deviation.
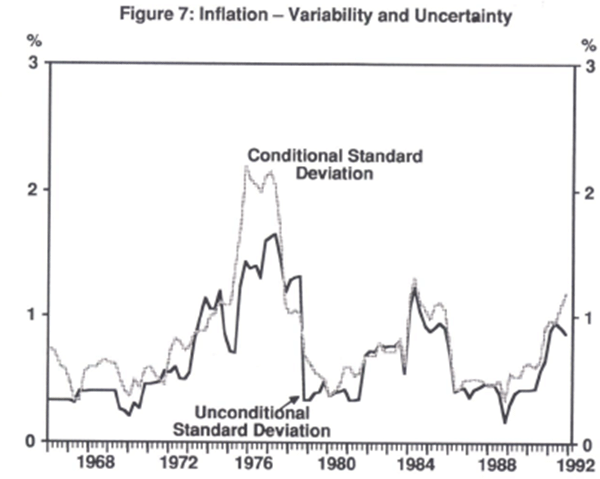
To get a measure of uncertainty, we estimated a recursive forecasting equation for inflation using only information available to agents at the time the forecast was made. The estimating equation contained four lags of inflation, real GDP growth and the growth rate of the M3 measure of the money supply. Additional variables such as interest rates and overseas prices did not add to the predictive power of the final equation. (Details are reported in Table B1 of Appendix B). Diagnostic tests on the estimated equation strongly reject the null hypothesis of homoscedastic errors. The forecast errors from the recursive prediction were then used to estimate an eighth order rolling (conditional) standard deviation. Figure 7 plots both the unconditional and the conditional standard deviations.[11] One interesting feature of this picture is that, contrary to a common assertion, inflation was generally less predictable and hence more uncertain during the 1980s than during the 1960s. However, both variability and uncertainty had fallen in the 1980s relative to the 1970s. As there is an apparent close relationship between the conditional and unconditional measures, there will be a corresponding relationship between the level of inflation and the conditional standard deviation. Thus it seems safe to conclude, in line with Pagan, Hall and Trivedi (1983) and Parkinson (1991), that the Australian data exhibits a positive relationship between the level of inflation and uncertainty.
4. Inflation, Interest Rates and Exchange Rates
A common approach to assessing the impacts of inflation, and thereby getting an indication of how costly inflation might be, has been to identify the effect of inflation on the prices determined in equilibrium in key markets. In particular, the impact of inflation on nominal and real interest rates is viewed as an indication of how much savings and investment decisions might be distorted. The impact of inflation on exchange rates is taken as an indication of how resources have been reallocated between the traded and non-traded goods sector as a result of inflation. We now consider some of these results.
(a) Interest Rates and the Fisher Effect
Whether or not savings and investment decisions are distorted by anticipated inflation depends on whether or not the real costs and returns to those activities are distorted. Thus, we are interested in the relationship between inflation and real interest rates.
In our benchmark inflation-neutral world, a fully-anticipated inflation is fully reflected in nominal interest rates. Following Fane (1990), consider a world where the personal and company tax systems are equivalent and fully integrated (company taxes are simply a withholding tax, or there is full dividend imputation), depreciation allowances are fully indexed, overseas and domestic income is treated equally for tax purposes, and only real interest receipts are taxable, while only real interest costs are deductible. In this world, only real income is taxed, and the simple Fisher effect would hold. That is:
where r is the anticipated real interest rate, i the nominal interest rate and π the anticipated rate of inflation[12]. Since there would be no change in real tax burdens as inflation changed, there would be no change in savings and investment decisions.
It is usually the case, however, that lenders are taxed on nominal receipts and borrowers are able to deduct nominal interest payments. If all other conditions remain the same then:
where rat is the after-tax real rate, and τ the marginal tax rate. In this world, the tax-adjusted Fisher effect holds. That is, the after-tax real rate is constant if, following a rise in inflation of one percentage point, the nominal interest rate rises by more to compensate for the increase in tax burdens as nominal incomes rise. In particular, for the tax-adjusted Fisher effect to hold:
Defining r(0) = (1 – τ)i(0) to be the real interest rate in a world with zero inflation, then the tax-adjusted Fisher effect equation can be rewritten:
That is, a permanent increase in inflation has two effects: first, i(0)π compensates the asset holder for the erosion of nominal income streams; and second, π/(1 – τ) compensates the asset holder for the capital depreciation incurred in the real value of the stock of assets. As Jump (1980) notes, the latter term is ‘marked up’ by a factor of 1/(1 − τ) because interest earnings are subject to tax, but capital depreciation is not.
In principle, there should be no change in borrowing or lending decisions if the tax-adjusted Fisher effect holds. But there are many possible ways in which the assumptions supporting the validity of the Fisher effect might not hold.
Suppose borrowers and lenders face different marginal tax rates. In particular, suppose that lenders face a higher marginal tax rate than do borrowers: τb < τl. Following an increase in anticipated inflation, in order to maintain real income it must be the case that:
The nominal interest rate lenders receive must rise by more than the nominal interest rate borrowers face. In general, the actual rise will be between that required for borrowers and lenders, so that the real return to saving declines but the real cost of lending increases. Since consumers tend to be net lenders and firms net borrowers, this particular tax distortion will lead to a reduction in both savings and investment.
Fane (1990) and Gruen (1990) consider the impact on the Fisher Effect of the international arbitrage conditions applying to an open economy. In a world where uncovered interest rate parity holds:
where θ is the expected rate of depreciation of the domestic currency. If ex ante purchasing power parity conditions also hold then, for a small country, increases in anticipated inflation must be fully reflected in the nominal interest rate, irrespective of the taxation system. Thus the simple Fisher effect is restored. But this means that the tax-adjusted Fisher effect cannot hold and the real after-tax return on saving falls, as does the real cost of borrowing. Ceteris paribus, savings falls and investment increases, funded by borrowing overseas.
Fane also considers the effects of differential tax treatment of domestic and foreign income. To maintain neutrality of inflation, that is for inflation to have no effect on real income streams, tax payments by Australians lenders on loans denominated in foreign currency should also be computed in real terms – foreign nominal interest earnings less inflation computed in terms of the foreign currency. But, in general, the tax payments are computed in nominal terms, and income variations resulting from changes in the exchange rate are included in the tax base. Thus, as inflation increases, and if the exchange rate depreciates, foreign incomes rise in terms of domestic currency and the tax burden rises. Conversely, for borrowers of overseas funds, an increase in inflation at home and consequent depreciation increases the interest costs of the overseas loan, reducing the domestic tax burden. Thus inflation may deter domestic investment abroad (and alter its composition, see Fane (1990)) and encourage overseas borrowing.
In general it would appear that existing nominal rigidities are sufficient so that it is unlikely that the tax-adjusted Fisher effect holds, and there might be significant effects on the allocation of real resources. The empirical evidence has been unable to settle the matter, although there seems to be a predominance of opinion against either the simple or the tax-adjusted Fisher effect holding.
In the United States, Summers (1983), using methods that attempt to insulate the results from the effects of short-run cyclical changes, concludes that nominal interest rates do not systematically incorporate an inflation premium into them.
Using Australian data Carmichael and Stebbing (1983) attempt to show that, in fact, nominal interest rates were roughly constant and real interest rates more or less adjusted one-for-one with inflation.[13] They dubbed this phenomenon the ‘inverted Fisher effect’. This result, that nominal interest rates did not adjust fully to reflect inflation, is hardly surprising over the sample used by Carmichael and Stebbing, as nominal interest rates in Australia before financial deregulation were largely controlled. Thus real after-tax interest rates could quickly become negative in periods of high inflation. Figure 8 shows this. But following financial deregulation in Australia, it would seem that there has been a return to something more like the existence of the Fisher effect – simple or tax-adjusted. Figure 9 indicates that since 1980 the nominal rate moves much more closely with inflation and the real rate after tax is positive and less variable (see Carmichael (1990)).
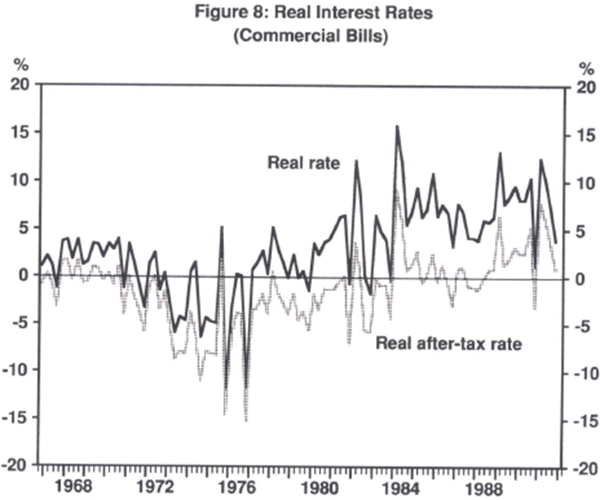
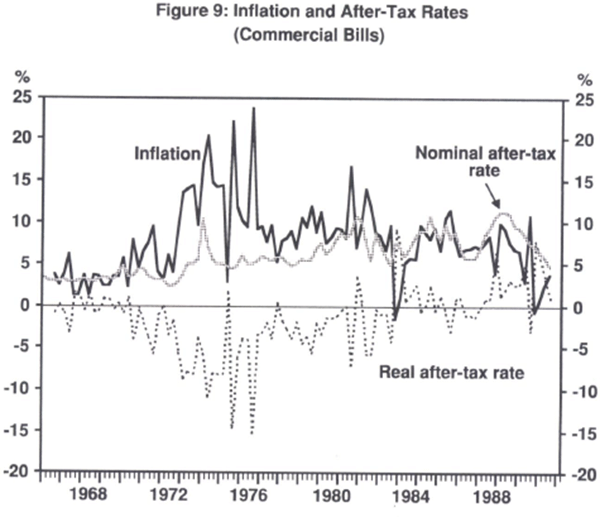
Bullock and Rider (1991) show that similar results hold across a number of OECD countries for roughly the same time periods. That is, they find it generally true that before the mid-1980s the nominal interest rate did not adjust to fully incorporate an inflation premium. However, they suggest that since 1985 there has been a positive relationship between inflation and real interest rates.
More recently, Silvapulle and Inder (1992), using methods for estimating cointegrating or long-run relationships in the data, have determined that neither the simple Fisher effect or the tax-adjusted Fisher effect hold for Australian data. Their conclusions suggest that Australian capital markets are closely integrated with world markets, such that the tax-adjusted Fisher effect cannot hold, and there must be some form of ‘price stickiness’ because the simple Fisher effect does not hold either. Lowe (1992) reaches a similar conclusion – that price stickiness interacts with inflation such that real interest rates are affected by monetary policy. If this is so, then it is unlikely that any version of the Fisher effect will hold. Lowe also shows that inflation affects the term structure of interest rates, as it appears to affect the slope of the yield curve.
In summary, it seems that there are enough significant nominal rigidities in the economy that it is unlikely that after-tax real interest rates are not influenced by inflation. At this stage it is not clear exactly how real rates are affected, but we can be certain that real resource allocations are different in a world with inflation than in a world without.
(b) Inflation and the Real Exchange Rate
Our interest in the Fisher effect stemmed from a desire for some metric by which to judge the effects of inflation on resources devoted to savings and investment. Similarly, we can interpret inflation-induced changes in the real exchange rate as a signal that resource allocations between the traded and non-traded goods sector have been distorted.
Our benchmark inflation-neutral world requires that domestic inflation have no real effects. In the context of an open economy, a rise in the domestic price level will have no effect if the relative price of domestic goods in terms of foreign goods is unchanged, the relative price of tradeable goods in terms of non-tradeable goods is unchanged, and the relative price of imported goods in terms of exported goods is unchanged. That is, inflation will be neutral if it leaves undistorted all of the various definitions of the real exchange rate. For this to be the case, the nominal exchange rate should adjust to reflect any changes in domestic prices that are purely the result of domestic inflation. This, of course, requires some version of purchasing power parity (PPP) to hold.
Following Dornbusch (1988), departures from PPP fall into one of two categories: those that arise in response to new and lasting changes in equilibrium relative prices – persistent real shocks – and those that occur as a result of disturbances to which the economy adjusts with differential speeds in goods and services markets. The latter deviations Dornbusch calls ‘transitory’ deviations.
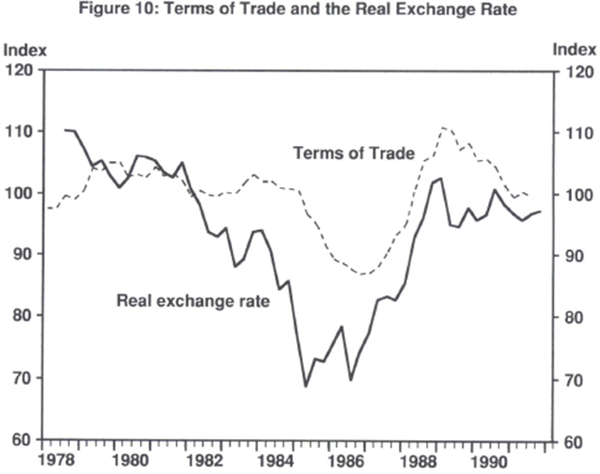
There is no controversy surrounding the assertion that real exchange rates will vary because either the terms of trade vary or because of differential rates of growth between countries. In particular, a fast growing country will have an appreciating real exchange rate. The argument is as follows: it is generally supposed that high growth countries have high average productivity growth which is uneven across sectors. In general the highest productivity growth rates are in the traded goods sectors, while the non-traded goods sector, mainly the services sector, exhibits lower productivity growth. But since wages within a country tend to be equalised across sectors, wages in the non-traded goods sector will be rising faster in the high growth country than in the low growth country. Thus the high growth country's prices of non-traded goods will be rising faster than in the low growth country. Further, as prices for traded goods will be equalised across countries, the average price level in the high growth country will be rising faster than in the low growth country. The real exchange rate will appreciate.
Fluctuations in the terms of trade will also induce systematic departures from PPP. For example, an exogenous increase in foreign demand for domestic goods will increase demand pressures in the domestic goods and services market, increasing prices. At the same time, there will be an increase in the supply of foreign exchange paying for the higher level of exports. The nominal exchange rate will appreciate. With domestic prices rising and the nominal exchange rate appreciating, the real exchange rate will appreciate.
In a small country like Australia, exporting a small bundle of commodities, we might expect the relationship between the terms of trade and the exchange rate to be very close. This can be seen in Figure 10.
Thus, there is no good reason to suppose that in the absence of inflation the real exchange rate will be constant. However, to the extent that there are nominal rigidities in the domestic economy, inflation will cause deviations in the real exchange over and above those which would otherwise have occurred. The existence of nominal wage contracts causing sluggish adjustments in wages is often advanced as an important reason for the existence of transitory deviations from PPP. One explanation depends on Okun's characterisation of markets as either auction or customer markets. In the former, prices are flexible and highly arbitraged. But in the latter, prices tend to be set on the basis of normal unit labour costs and tend to be ‘sticky’. When domestic inflation increases, prices in the traded goods sector adjust faster. The nominal exchange rate might adjust so as to maintain competitiveness in the traded goods sector with foreign goods. But with sluggish non-traded goods prices, the relative price of non-traded goods in terms of traded goods falls and domestic demand switches from traded goods to non-traded goods. The real exchange rate appreciates. Resources are diverted from the traded goods sector into the non-traded goods sector. This adjustment is facilitated as wage pressures build up in the non-traded goods sector and flow into the traded goods sector.
Alternatively, one could make the case that non-traded goods markets, typically being markets in services, are more sensitive to menu costs type arguments which increase the costs of changing prices in an inflationary period, again leading to sluggish price adjustment and real exchange rate appreciations.
Variations in the real exchange rate, to the extent that they persist, will induce a variety of resource misallocations. In the first instance, variations in the real exchange rate will induce variations in profitability, and so real resources will be reallocated between the traded goods and non-traded goods sector in ways that they would not have done in the absence of inflation. Alternatively, because inflation will induce variability into the real exchange rate that would not have existed with no inflation, it will be harder for individual agents to filter out of real exchange rate movements those emanating from, possibly long-run, real disturbances to which they should respond, and those which are purely the result of inflation's interaction with the economy's nominal rigidities.
Krugman (1989) offers an interesting model dubbed the ‘sunk cost model’ which attempts to explain why traded goods prices might be sticky in the face of large exchange rate movements. In short, Krugman postulates that foreign trade is ‘hard’, and that once a firm is successful, it will not easily give up foothold in a foreign market in the face of variations in real returns caused by exchange rate movements. Conversely, we can argue that if this is the case, large anticipated exchange rate movements will deter firms from even attempting to break into foreign markets, realising as they do the large fixed costs of so doing. In a report on Australia's export performance, Hughes (1989) noted that ‘exporters identify foreign exchange volatility and foreign exchange overvaluation as the principal determinant of their export difficulties’.
(c) Summary
It seems clear from the discussion in this section that there are many ways that inflation interacts with the various nominal rigidities in the economy to divert resources from uses they would have undertaken in the absence of inflation. However, there is a significant difficulty encountered when attempting to gauge the costs of inflation from its effects on relative prices. That is, relative prices could have changed as a result of inflation, but the equilibrium quantities determined in the market might remain unchanged. The extent of welfare loss due to inflation depends on just how resources are diverted form their original use. In other words, in equilibrium, we cannot gauge from the size of relative price changes the size of real resource misallocations. For this reason we now turn to an examination of inflation's effects on employment and investment.
5. Inflation and the Markets for Labour and Capital
(a) Inflation and Employment
Inflation can interact with the outcomes in labour markets in a number of ways. First, if wage adjustments are sluggish, say because of the existence of nominal wage contracts, then inflation will erode real wages and possibly increase employment. This is one of the foundations underpinning the existence of a positively-sloped short-run aggregate supply curve (negatively sloped short-run Phillips curve). As discussed in Section 2, in the absence of macroeconomic externalities, the increase in output should itself be regarded as cost. In an externality-free world, any deviation from the inflation-neutral level of output incurs costs as it represents an outcome that private agents would not have chosen in an inflation-free world.
Even if we do not measure the costs of inflation as positively related to the absolute value of the output gap, inflation in labour markets will have impacts on the types of contracts workers enter into. Because it is the existence of fixed nominal contracts that leads workers to supply more labour for lower real wages, an increase in the variability of inflation will lead to shorter average contract lengths. Carlton (1982) shows that in markets where agents can insure against future price changes, a rise in inflation, and presumably its variability, leads to an increased number of transactions in futures markets and liquid spot markets and a reduction in transactions in illiquid and customised markets. In the market for labour, which by its nature trades a very heterogenous good precluding the use of futures contracts, this will mean shorter contracts and less contract diversity.
Christofides and Wilton (1983) investigate endogenous contract length in a study involving nearly 2000 Canadian wage contracts. They find that contract length varies positively with the costs of contracting and negatively with uncertainty regarding inflation. They find that as uncertainty about inflation varies from its low point to its high point in the sample, average contract length falls by over 14 months. The problem of renegotiating contracts thus becomes more important, and more resources are devoted to this essentially unproductive activity.
The interaction between inflation and the rigid nominal personal income tax scales is often thought to be the greatest problem caused by inflation in the labour market. Statements to the effect that inflation pushes workers into higher tax brackets, increasing their real tax burden, or reducing their after-tax return to labour, thus destroying incentives to work – reducing the supply of labour – abound. But as Carmichael (1990) notes, the increase in the effective tax burden has both substitution and income effects. By reducing after-tax returns to labour, inflation and the tax system reduce the opportunity cost of leisure and so increase the demand for leisure, reducing the supply of labour. Other things constant, pre-and after-tax real wages must rise. This increase in real wages, in excess of what would have occurred in the absence of inflation, has a number of distorting effects. First, the relative price of labour intensive goods rises in terms of capital intensive goods. Second, the relative price of non-traded goods in terms of traded goods will rise if, as is commonly assumed, non-traded goods are typically labour-intensive services. And the relative price of domestic goods in terms of foreign goods will rise.
However, other things are not usually constant. In particular, worker after-tax take-home income falls, possibly inducing an income effect. But whether or not an aggregate income effect exists depends on what happens to the inflation generated revenue collected by the government as effective tax burdens increase. If the government spends the increased tax revenue in a way in which the workers might have spent it, had they been given the choice, then there is no aggregate income effect. That is, if workers, at the margin, value government spending (in this case the government cannot be ‘too big’), so that the ‘social wage’ is unchanged, then there is only a substitution effect and inflation will have distorting effects, reducing equilibrium employment.
On the other hand, if workers believe that the government is ‘too big’, so that government spending at the margin has little or no value to workers, then there is an aggregate (negative) income effect, real income is reduced and the supply of labour will increase. The net effect depends on the relative sizes of the substitution and income effects, about which little can be said.
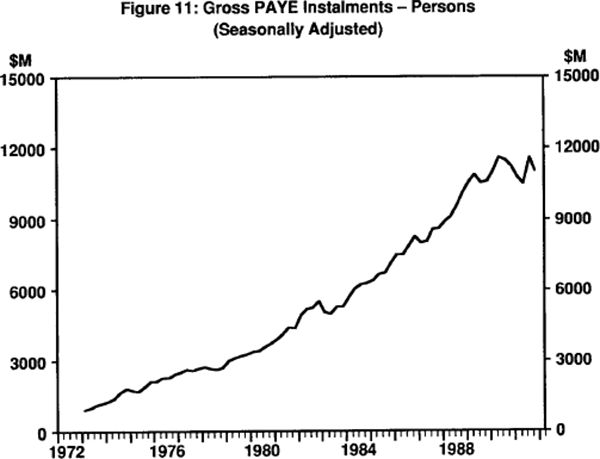
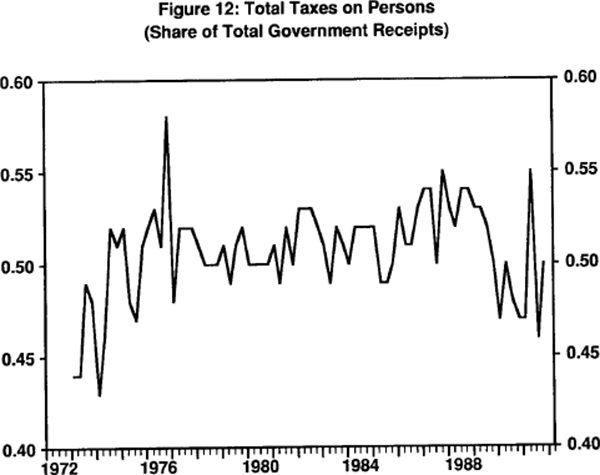
In any case, as has been pointed out, the periodic adjustments made to the tax scales over the 1980s have left the real tax burdens on workers largely unchanged.[14] Figures 11 and 12 indicate the extent of the changes. Figure 11 shows the total gross PAYE instalments by persons. The upward trend, under the influence of inflation is clear. However, Figure 12 shows the taxes on persons as a share of total taxes. There is no trend evident since the mid-1970s, and personal income taxes as a share of total taxes may even have fallen in the late 1980s. Of course, this is not to suggest that total tax burdens have not risen. Rather, it suggests that the work incentive effects of the interaction between inflation and nominal personal tax scales may have been overstated.
There are other possible avenues through which inflation can have adverse effects in the labour market. One possible source of concern for workers negotiating wage contracts is the variability of inflation. If workers could fully anticipate the extent to which inflation will erode the real wage over the life of a contract, then that information could be incorporated into the contract. However, variable inflation will induce risk averse workers to negotiate a nominal wage that incorporates a premium to cover the event that the realised price level is higher than the expected price level. In other words, contracts will be negotiated to guard against the possibility of an unexpectedly low real wage outcome. Thus, increasing uncertainty about inflation, which is closely related to increasing variability of inflation, will push up the average nominal wage rate and hence the real wage. If monetary policy is exercised to accommodate a wages policy, as Carmichael (1990) and others acknowledge[15], then increases in the average level of inflation may be caused by increases in the variability of inflation.
Appendix A briefly elaborates on a model displaying the above characteristics. It suggests that the nominal wage rate should be directly proportional to the average level of prices and positively related to the variability of both inflation and employment. In the absence of variability of inflation and unemployment, the nominal wage would be set so as to maintain the real wage. But, in the presence of uncertainty regarding both employment and inflation, the nominal wage will be set with an inflation/uncertainty premium. Thus, the real wage will increase with uncertainty, from which it follows that high and variable inflation may be the cause of a wage-price spiral, in contradistinction to the more common argument that increases in real wages are the triggering factor for inflation.[16] This is the conclusion reached in an atheoretical paper by Mehra (1991), in which on the basis of sophisticated causality tests he concludes that prices cause wages and not vice versa. Hirsch and Addison (1988) also provide evidence for this hypothesis.
The model outlined in Appendix A is a contracting model with the real wage depending on information available at the time the contacts were negotiated. In an attempt to gauge the size of these influences, a simple reduced-form real wage equation with the following specification was estimated:
The RWAGE was measured as average earnings deflated by the CPI, INF as the quarterly inflation rate of the CPI, VINF as a four year recursive standard deviation of INF, and VUNEMP as a four year recursive standard deviation of UNEMP. Results are reported in Table B2 of Appendix B. Since both RWAGE and UNEMP are integrated processes, the model was estimated both in levels and differences.[17] The data are described in detail in the Data Appendix. Because both the level of unemployment and the real wage are jointly determined in equilibrium, instrumental variables were used in the estimation.
Though not definitive, the results are encouraging. Leaving the variability variables out of the estimation places explanatory power back on inflation, so that real wages and inflation appear to be positively related. Thus, inflation in a real wage equation may simply be proxying for uncertainty. The variability of inflation is consistently positive and significant, whereas uncertainty about unemployment is not generally significant. It is certainly true that much of the explanatory power of the model in levels derives from common factors in the underlying processes for both the real wage and unemployment, as the explanatory power of the differenced model falls considerably. At the very least, these results suggest that estimated wage equations which do not account for uncertainty may be misspecified.
If the real wage varies positively with inflation, and/or inflation variability, then this would have implications for aggregate measures of income shares. In particular, with real wages rising during, and because of, high and variable inflation, the wages share should also increase. This appears to be the case. Figure 13 shows the gross income share (wages, salaries and supplements) and the rate of inflation.
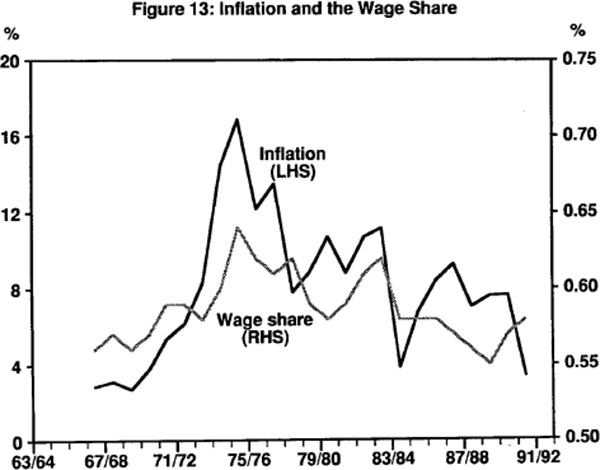
The wage share rose dramatically in 1973/74 following the rise in inflation. Again, in 1981/82, the rise in inflation preceded the wage explosion. However, the econometric evidence does not appear to support the conclusion that the wage share depends positively on the rate of inflation. Upon examination of the data, we could find little direct influence of inflation or inflation variability on the wage share. The level of industrial disputes does appear to have an effect, however, possibly indicating that inflation effects operate indirectly through the negotiation process. In order to bring about an increase in the real wage and wage share in a contracting framework, one might expect that negotiations are more frequent and perhaps, less amicable. This appears to be the case.
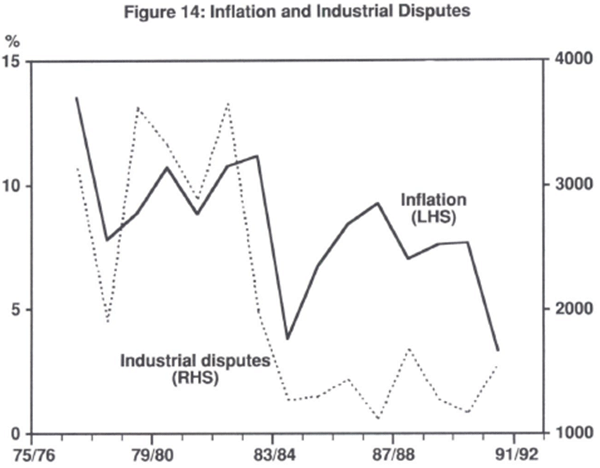
Figure 14 shows the graphical relationship between industrial disputes and inflation. It seems that the level of inflation itself has little effect on the level of industrial disputes in Australia. However, there is a significant positive correlation between uncertainty about inflation and industrial disputes. This result is also found in Siebert and Addison (1981) for U.K. data, where they suggest that uncertainty about inflation complicates the inferential task of negotiators and leads to more mistakes – strikes – occurring. Hirsch and Addison (1988) discuss several studies finding a positive correlation between inflation uncertainty and strike activity.
Given that there appears to be some interaction between inflation and the real wage, the wage share and the negotiation process, we might expect to see this manifest in the level of employment. To test this assertion an employment equation in the spirit of Russell and Tease (1990) was estimated. Using their specification and annual data, the results were very similar. However, we could not find any consistently significant effect of either inflation or the variability of inflation on the level of employment, or its growth.
(b) Inflation and the Capital Stock
Inflation interacts with incentives to invest in various well understood ways. Vann and Dixon (1990), Ryan (1990), Willmann (1990) and Freebairn (1991) provide useful discussions of the Australian case. Feldstein (1983) provides a comprehensive survey of the U.S. case.
As Vann and Dixon note, inflation creates problems with investment because it distorts measures of the tax base when assets last more than one period. Since we have already discussed the interaction between inflation and interest rates, we briefly discuss other interactions below.
(i) Inflation and Depreciation
If all equipment lasted only one period, then businesses would not need to account for the gradual run-down of equipment, and the need to cater for its replacement in the future. Inflation distorts this process when accounting systems operate on an historical cost basis, and not replacement cost. With inflation, most depreciation rules are such that the real value of depreciation allowances is eroded, and thus the true extent of depreciation is understated.
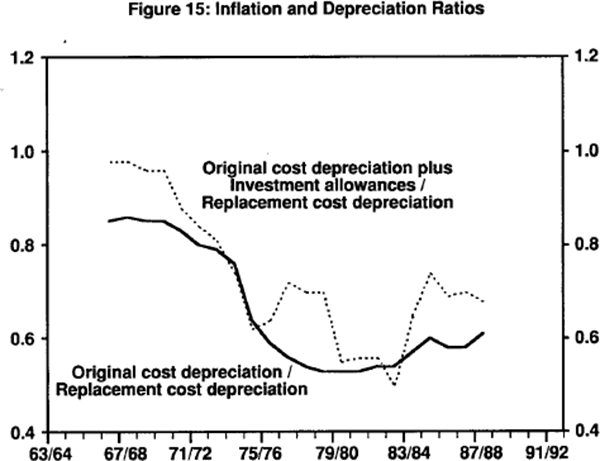
In Australia, various adjustments to depreciation formulas have been adopted – accelerated depreciation, the ‘5/3 system’ and various investment allowances – but these have rarely compensated for the effects of inflation. Figure 15 shows data taken from Willmann (1990) (Table 2). The Figure shows the ratio of original cost to replacement cost, indicating the impact of inflation on capital values. Total deductions, including allowances, are also shown. It is clear from the Figure that inflation significantly distorted the value of depreciation allowances and so significantly penalised investment in plant and equipment. While it is generally thought that this penalty increases with the length of the equipment's effective life, Ryan (1990) argues that this effect is probably overstated as depreciation becomes less economically significant the longer a project's life.
(ii) Inflation and Stocks
The first-in-first-out accounting method used by Australian companies measures the costs of inventory or stock at book value. If the price of the products are rising in inflationary periods, the sale price of the goods exceeds the book value or cost, and the firm is seen to be making profits. The tax obligation of the firm is overstated because it contains a capital gain on stocks, purely the result of inflation. This imposes a penalty on holdings of inventory, and actual inventory holdings will fall below levels that would have been optimal in an inflation-free world.
(iii) Inflation and Capital Gains
Up to 1985, when a capital gains tax was introduced in Australia, a bias was created for firms to undertake investments in projects which yielded returns in the form of capital gains, rather than income. While this distortion has since been removed, there still remains a significant distortion between investment in housing and other forms of investment as owner-occupied houses are not subject to a capital gains tax.
(iv) Inflation and Cash Flows
Most investment projects involve the deferral of cash flow. Projects usually account for losses early and gains later. As Ryan (1990) notes, the various interactions between inflation and the nominally rigid Australian accounting and tax systems tend to exacerbate the typical cash flow pattern. If capital markets were perfect, and in the absence of uncertainty, then this would not create a problem. But various liquidity constraints arise in capital markets. And, uncertainty tends to increase with inflation compounding the problem.
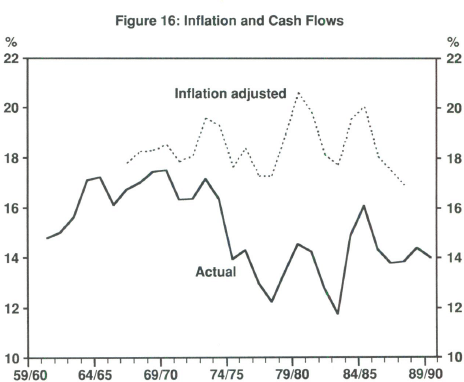
With data provided by Willmann (1990) we can get some idea of the extent of the distortions. Following Pagan and Gray (1983) we define the cash flow to be:
where CASH is cash flow, YC is income before the stock valuation adjustment, DEP is depreciation and deductions, and SVA is the stock value adjustment. All these data, for corporate trading enterprises, are in the National Income Forecasting Model (NIF-10) database. Willmann estimates, for corporate trading enterprises, the extent of depreciation allowance understatement, and other various distortions which tend to overstate company income, and thus lead to excessive tax obligations. Using her figures for the correct allowance for depreciation, and adjusting the tax obligations of corporate trading enterprises, we can derive an inflation-adjusted measure of what cash flow should have been in an inflation neutral world. Figure 16 shows the extent of the impact of inflation on cash flows. Its significance is apparent.
(v) Inflation and Investment
Given the extent of the distortions caused by the interaction of inflation and the various nominal rigidities under which companies work, it might be expected that inflation has a significant negative effect on the level of investment, and hence on the capital stock. This is indeed the case, although it is not a straightforward matter to demonstrate it.
Pagan and Gray (1983) (PG hereafter) estimate an investment equation for corporate trading enterprises (CTEs) based on the neoclassical model. Their result is:
where IEQ is the investment ratio (investment in plant and equipment as a fraction of the existing capital stock), RET is the gross after-tax rate of return on investment (gross operating surplus less tax payable as a fraction of the value of the capital stock), and IA is a dummy variable for investment allowances. The data are described in the Data Appendix.
From the above equation, one could then calculate the change in the capital stock, via distorted investment decisions, by utilising Willmann's data. The interaction of inflation and the tax and accounting systems increased the tax burden of CTEs, and depressed the gross rate of return on capital. However, apart from scaling differences, it proved very difficult to replicate PG's results using updated data. There are two reasons for this. First, PG construct some of their own data. Most of the data are now available in the NIF-10 database and, on inspection, there proved to be some differences. In particular, PG's measure of the value of the stock of plant, equipment and other structures is somewhat bigger than the official statistics.
However, the major reason why their results are now no longer obtainable is that there appears to have been some structural changes in investment behaviour since 1983. Re-estimating PG's investment equation over the period 1963 to 1983 yielded qualitatively similar results to theirs. However, when the sample was extended to 1991, the results broke down. Analysis of the structural stability of the coefficient of the rate of return variable showed a marked decline in its size.
Further analysis revealed that a cash flow variable, RCASH, defined:
filled the role of RET previously. Moreover, both inflation and the variability of inflation had significant effects on the rate of investment. A reasonable representation of the data is:
for the 1963 – 1983 sample period, and:
for the 1963 – 1991 sample period.
Various specifications were tried, with varying success. Similar results hold when the supply price of capital is used instead of the cash flow variable. The rate of return variable consistently performed poorly. However, uniformly, the effects of the level of inflation were significant and negative, with a stable parameter estimate. Similarly for the variability of inflation, although here the parameter estimate was consistently positive.
Thus inflation has three clear influences on investment. First, it defers immediate cash flows of firms, reducing the profitability of future investment. To the extent that cash flows continue to be deferred, to all intents and purposes inflation reduces cash flow. Second, inflation has a direct negative impact on the rate of investment, over and above those working through cash flows. And third, the variability of inflation has a direct effect, although its positive influence needs to be explained.
The cumulative effects of inflation on investment can be seen in Figure 17. The Figure shows the actual investment ratio (plant and equipment for CTEs) and what it would have been had firms' cash flows been insulated from the effects of inflation, and if inflation and its variability had been zero. The discouraging effects of inflation on the level of investment are clear.
These figures indicate that in the absence of inflation over the period 1966/67 to 1988/89 investment by CTEs in plant and equipment, as a fraction of the existing capital stock, would have been at a minimum 2 per cent higher in 1966/67, 4 per cent higher in 1985/86, and over 25 per cent higher in 1982/83 and 1983/84. On average, with inflation constant at zero, investment in plant and equipment would have been around 14 per cent higher. Of course, much of this reduction in investment in plant and equipment may have been offset by increases in other forms of investment, as we discuss next.
(vi) Inflation and the Investment Mix
Apparently investment behaviour in Australia changed around or after 1983. What it is not clear from the aggregate data is the changing mix of investment and the changing methods of financing. Kent and Scott (1991) show that, while aggregate investment was strong over the latter half of the 1980s, real estate operators and developers, various insurance and finance industries and other property industries accounted for almost fifty per cent of total real private non-rural investment between 1985/86 and 1988/89. Kent and Scott note that some of this investment might have simply replaced investment in building and structures that original users might previously have undertaken on their own behalf. Nonetheless, the figures tend to confirm a common perception that much of Australia's recent investment has been in ‘unproductive’ housing and property.
That investment in plant and equipment should fall, as is evident from Figure 17, is important in the context of recent work by De Long and Summers (1991). They show that investment in plant and equipment has a stronger association with economic growth than does any other category of investment, and they attribute causality from investment to growth, not growth to investment. In this light, if, as we have shown, inflation tends to reduce investment in plant and equipment, redirecting it into other forms of investment (primarily property based), then we can expect that economic growth will slow down.
Coupled with the redirection of investment, Macfarlane (1989, 1990), amongst many others, has discussed the changing relationship between debt and other forms of financing in Australia. A major theme of this work is that the interaction of inflation with the tax system induces firms and individuals to borrow and accumulate debt. That is, inflation has affected the demand side of the debt problem. While this is true, the discussion so far has largely ignored the effects of inflation on the cost of equity financing versus debt financing.
Given our discussion above, the value of firms will be directly and negatively effected by inflation as they are induced into actions they would not otherwise have chosen in an inflation-neutral world. This negative correlation between inflation and the value of firms, as measured by a stock market aggregate, is well documented in the United States (see Feldstein 1980, for example)[18]. A similar relationship appears to hold in Australia. Figure 18 shows the value of the All Ordinaries index, deflated by the GDP deflator, against the rate of inflation (measured by the CPI).
The negative correlation is apparent up to 1985. Since then the relationship may have changed. If the real value of firms falls with inflation, and lenders require a given real rate of return on equity, then equity financing will become more expensive. At the same time, tax benefits are conferred on debt financing with the full tax deductibility of nominal interest payments.
Thus, with inflation, the average costs of funds will probably rise, but the relative cost of debt financing in terms of equity financing will fall.
(vii) Dividend Imputation and Other Deregulations
It might be argued that many of the costs we have been elaborating on have been removed or, at the very least, minimised by the string of deregulatory changes that have occurred in Australian markets over the 1980s. Of particular importance here is the introduction of dividend imputation. One might argue that to the extent inflation overstates the nominal income, and hence tax obligations, of firms, it reduces the tax obligations of individual shareholders. In other words, the interaction between inflation and the various nominal rigidities simply diverts cash flow away from firms to individual shareholders. This distortion might have no impact on the aggregate level of investment if shareholders and firms have the same propensity to save and invest out of income – an unlikely proposition. And even if shareholders and firms did exhibit such a characteristic, it is unlikely that they would choose the same portfolio of real and financial assets to invest in. Shareholders do not have the same opportunity as firms for investing in real plant and equipment, except through purchases of equity. Thus if cash flow streams are diverted away from firms to shareholders, where those cash flows would have ended up as expenditure on plant and equipment, they would now be distributed as expenditure over a variety of real and financial assets, but not plant and equipment. We could therefore expect that even if the aggregate level of investment was unaffected, the mix would be significantly distorted away from investment in plant and equiment into other forms of investment.
The same reasoning applies to considerations of the effects of inflation via the Tobin effect. It is sometimes claimed that since inflation reduces the real return on cash, it induces increased expenditure on capital goods, hence increasing the country's capital stock. If this does indeed happen, whether or not it is welfare enhancing depends on a variety of considerations, including those canvassed earlier in this paper. That issue aside, however, a more important question is whether or not the Tobin outcome actually prevails. Once again, heterogeneous investment opportunities would seem to be significant. Shareholders are more likely to be holding cash for wealth purposes than are firms. As the real rate of return for cash falls, it is the portfolios of shareholders which will be adjusted, and those portfolios typically do not include opportunities for direct investment in plant and equipment. Investments may well be directed to real assets such as land and housing as an inflation hedge, but not to machinery and factories.
In short, one can point to a number of recent changes, and other considerations, which in a simple world might reduce the costs of inflation. However, when one further considers that the world is a very heterogeneous place, with different classes of savers and investors having differential access to alternative investment opportunities, it is by no means clear that the favourable outcomes have prevailed. My hunch is that significant distortions in the investment mix, shifting that mix away from plant and equipment towards housing and other sectors accessible to non-firm savers and shareholders, has occurred following some recent deregulations.
(c) Summary
Inflation has important and identifiable effects in the markets for factors of production. It interacts with the functioning of the labour market as workers react to expected and unexpected inflation when entering into nominal wage contracts. Inflation has clear distorting effects in the market for capital by its interaction with various nominal rigidities. Our back-of-the-envelope calculations suggest that inflation could significantly reduce the rate of investment in plant and equipment, and this would have a significant effect on marginal and average labour productivity. It follows then, that the effects of inflation should be identifiable in the aggregate output data. We now turn to this issue.
(d) Inflation and Output
In section 2 we discussed the difficulties faced with trying to identify the effects of inflation of output. To briefly summarise, the most significant difficulty is that inflation itself is endogenous and, at least in the short-run, determined by factors other than just monetary policy or other government policy. Thus isolating cyclical effects from inflation induced effects is important. To overcome this problem, many studies on the costs of inflation use cross-sectional data covering a range of countries. Alternatively, they use period averages to wash out the cyclical effects at the expense of considerable information loss.
An interesting cross-sectional study is provided in a recent paper by Cozier and Selody (1992). They base their work on a neoclassical growth model, which explicitly considers human capital. That is, their approach is similar to that taken in this paper in that underlying factors of production and the effects of inflation thereon are examined. Cozier and Selody base their empirical results on 25 years of data from 62 countries (using the Summers and Heston database, including Australia) and conclude that inflation has significant effects on total factor productivity. They claim that a one-percentage-point reduction in inflation raises the rate of growth of income by about 0.1 percentage points along the transition path to a new level of income that is about 3 per cent higher after 30 years.
Other cross-sectional studies reach much the same conclusion, with roughly the same orders of magnitude. Kormendi and Meguire (1985) find that a one-percentage-point reduction in inflation leads to a 0.5 percentage increase in the growth of output. Grier and Tullock (1989) find the increase in income growth to be 0.16 percentage points for each one percentage point reduction in inflation.
Some time-series studies have reached the same conclusion. Jarret and Selody (1982) estimate that a one percentage point reduction in inflation would increase the rate of growth of labour productivity by a 0.3 percentage point. Novin (1991) updates their study yielding a 0.2 percentage point increase in the growth of labour productivity. Clark (1982), Buck and Fitzroy (1988), Selody (1990), Alexander (1990) and Grimes (1991) reach similar conclusions.
Kryiakopoulos (1990) is one of the few recent works to find no evidence that inflation lowers long-run growth.
Generally speaking, all the above works find that inflation has negative impacts on labour productivity. This would follow from our discussion because inflation significantly reduces the rate of investment, as well as distorting the investment mix, leaving workers with less productive capital to work with. Hence productivity falls. Productivity would fall further if significant labour resources, previously productively used, are now applied to the negotiation and renegotiation process as a result of inflation.
Not with standing the difficulties that plague single-country times-series studies of the effects of inflation, some simple experiments were tried and the results reported below. First a simple production function was estimated. A typical approach (see for example Carmichael and Dews (1989)) is to estimate a Cobb-Douglas function of the form:
where α + β = 1, and νt is assumed to be a first order autoregressive error process:
where εt is white noise. In general, νt is assumed to pick up omitted elements of technological progress and other unspecified influences on aggregate output. In log-form, the equation estimated is:
where y is the log of output per hours worked, and k is the log of the capital to hours worked ratio. All the results reported below used the total stock of plant and equipment as the capital variable.
Using annual data for Australia, 1966/67 to 1990/91 yields:
While the results are standard, the significance of the autoregressive term really needs to be explained. One possibility is that it is picking up some of the systematic influence of inflation. To test this hypothesis, a more general form of the production function was posited:
This specification yielded the following:
The simple addition of inflation and its variability does not alter the picture much. But we have contemplated a more complex interactive effect for inflation, leading to the following specification where inflation directly effects the way labour and capital are used, as well as the way they are combined:
Restricting the sum of the expanded exponents to equal one yielded the following equation (in logs) to be estimated:
with the following results:
Of all the parameterisations, this non-linear specification is the best statistical description of the data. This parameterisation of inflation's effects picks up almost all of the information previously picked up in the autoregressive error structure. The results suggest that the level of inflation has a consistent negative effect but the variability of inflation has a positive effect (as it did with investment).
However, the difficulty with this specification is that imposing the condition that the expanded exponents sum to one renders the net effect of inflation dependent on the capital/labour ratio, which is unit-dependent. Given the above results, the effects of inflation wash out. This would change if a different measure of the capital/labour ratio was used. However, it is not reasonable to restrict the production function to display (inflation adjusted) constant returns to scale. After all, the point of the exercise is to determine whether, for given inputs, less output is yielded when inflation is high. Relaxing the homogeneity assumption requires estimating the production function in levels with no constraints placed on the exponents. Preliminary results suggest that the unrestricted model is a good description of the data. Of interest is the fact that the sum of the estimated inflation dependent coefficients on labour and capital is not significantly different from one when inflation is low, but falls considerably below one (to a minimum of around 0.6) when inflation is high. This suggests that, in fact, inflation has a strong negative influence on production. But at this stage the results suggest an implausibly large effect. Moreover, the implied variation in factors shares is very large. Nonetheless, an approach to estimating the production function which allows the parameters to be dependent on inflation and other influences may prove profitable.
A direct measure of the costs of inflation could have been derived by using the inflation-adjusted investment series to construct an inflation-adjusted capital stock series. This series could then have been input into the (simple) production function to get a measure of the reduced output due to the reduced capital stock. There are a number of minor problems to be overcome in doing this and, at this stage, back-of-the-envelope type calculations seem as good as any other.
Take the elasticity of output with respect to capital to be around 0.35 (α in the simple production function). If average inflation (of around 7 per cent) reduces the level of investment by about 15 per cent (compared to zero inflation), which after allowing for replacement investment would yield a reduction in the capital stock of about 5 per cent, then average inflation reduces output by about 1.75 per cent (0.35 times 5). This translates roughly into a one percentage point reduction in inflation increasing the level of output by about 0.25 percentage points in the long-run – a figure in line with that obtained in numerous other studies.
Based on these numbers we can calculate the amount of output foregone because of inflation. Taking 0.25 as the annual percentage real GDP loss due to a one percentage point increase in the inflation rate, and compounding that figure at the average rate of real GDP growth from 1970 to 1991 (3.26 per cent per annum), then the cumulative loss in real GDP caused by the permanent one per cent increase in inflation in 1970 amounts to nearly 14 billion 1984/85 dollars (about $660 million a year), or about 5 per cent of current real GDP.
The cost from having average inflation at 7 per cent per year and not zero since 1970 amounts to forgone cumulated real GDP of almost $100 billion (1984/85 dollars), or about 35 per cent of current real GDP (spread over 21 years). By any standards, these are large costs.
These costs are, of course, the long-run steady state costs of inflation. From a policy perspective, one must weigh these costs, or benefits from reducing inflation, against the costs that would be incurred if a strict anti-inflationary regime was pursued.
6. Conclusions
There is no doubt that inflation has effects on the real economy. In the labour market, inflation's biggest effect is probably on the negotiation process workers and firms enter into when settling on wage contracts. Inflation and variability of inflation will induce firms and workers to negotiate more often, while at the same time muddying information and increasing the probability that ‘mistakes’ occur, leading to confrontation and strikes. With respect to capital, inflation increases the real tax burden of firms, reducing real cash flows and increasing the cost of equity financing. The capital stock is lower with inflation, more heavily biased towards assets other than plant and equipment and financed increasingly with debt. These results are also obtained by Kydland and Prescott (1980), who note that:
‘More surprising, at least to us, is the large effect that changes in anticipated future inflation rates have upon the capital stock. A change in the average inflation rate from zero to 7 per cent more than offsets the effect of a 10 per cent investment tax credit…’
It would appear that inflation's effects on the capital stock are the most important source of the costs of inflation.[19] In addition, inflation also distorts the production process, so that the reduced levels of inputs are used in less efficient techniques of production.
Since both labour and capital, and the aggregate technology are all adversely affected, inflation significantly reduces the level of output. Our back-of-the-envelope calculations, which are in line with a large body of international evidence (mainly cross-sectional studies which avoid the pitfalls associated with single country time-series studies), suggest that by adopting and achieving a zero inflation outcome, real output would be about 1.75 percentage points higher each year – or nearly 5 billion 1984/85 dollars bigger in 1991.
Appendix A: A Simple Wage Contracting Model With Risk-Averse Workers
We sketch below a simple model wherein risk-averse workers enter into wage and employment contracts with a risk-neutral firm. The workers and the firm agree upon a nominal wage before the price of the firm's product is realised. The firm then determines how many workers to lay off, if any, and production follows. Thus, workers must account for uncertainty about the price level, which will affect their real wage, and also uncertainty about employment – they could be laid off with no wage.
The Firm: Consider a representative firm which has on hand a given workforce N loosely tied to the firm by past hiring practices. Following the realisation of the price level Pt, the firm actually employs Lt workers at an average wage which is contracted in the previous period, t−1Wat. Thus the firm solves:
choosing Lt and Yt, subject the technology
where eut is a random productivity shock. The optimal level of employment, in logs, for the firm is given by:
(where lower case denotes logs of upper case variables). Define Λt = Lt/N, or in logs λt = lt – ln(N), to be the proportion of the potential workforce hired by the firm. Workers view λt as a random variable.
Workers: Workers attached to a firm agree to a wage and probability of employment before seeing the price level Pt. Suppose that fluctuations around average values are small enough so that workers view both the price level and the level of employment as normally distributed random variables. That is, they hold beliefs:
and
where νpt and νλt. are conditional means and
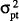 and
and
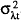 are conditional variances.
are conditional variances.
Suppose each worker takes the average wage as outside his own influence and maximises a utility function:
where:
ct is the random level consumption workers receive each period. If workers have opportunities outside the firm given by:
then the contracted wage will be set to satisfy:
The solution to this equation is:
That is, the contracted nominal wage is directly proportional to the expected average price level, and positively related to the variability of both prices and employment.
Appendix B: Regression Results
| Regressor | Lag | ||||
|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | |
| Constant | −0.5044 (−1.91) |
||||
| INF | 0.1410 | 0.2260 | 0.1874 | 0.2286 | |
| (1.54) | (2.46) | (2.04) | (2.52) | ||
| GDPG | −0.0100 | 0.0207 | 0.0211 | 0.0199 | |
| (−0.61) | (1.28) | (1.30) | (1.22) | ||
| M3G | 0.0762 | −0.0204 | −0.0607 | 0.0626 | |
| (1.81) | (−0.27) | (−0.83) | (1.4) | ||
| R2 0.58 | DW 1.89 | SER 0.81 | |||
| Regressor | Model | ||||
|---|---|---|---|---|---|
| Levels | Differences | ||||
| Constant | 0.0610 (24.9) |
0.602 (23.7) |
0.638 (12.0) |
0.014 (2.6) |
0.012 (1.6) |
| UNEMP | 0.036 (8.97) |
0.040 (7.6) |
0.036 (3.9) |
−0.002 (−0.2) |
0.002 (0.3) |
| UNEMP−1 | −0.039 (−1.2) |
−0.043 (−0.8) |
−0.002 (−0.2) |
−0.010 (−0.3) |
|
| INF−1 | 0.010 (3.58) |
0.006 (1.7) |
−0.001 (−0.2) |
0.002 (1.1) |
0.001 (0.6) |
| VINF−1 | 0.017 (1.4) |
0.042 (2.4) |
0.014 (2.4) |
0.014 (2.2) |
|
| AR(1) | 0.270 (0.64) |
0.408 (1.2) |
|||
| R2 | 0.87 | 0.88 | 0.89 | 0.27 | 0.41 |
| DW | 1.33 | 1.21 | 1.52 | 1.3 | 1.95 |
| SER | 0.045 | 0.045 | 0.040 | 0.023 | 0.022 |
Appendix C: Data Sources
Apart from the data used in Figures 15 and 16, which is found in Willmann (1990), all the remaining data were taken from various databases supplied by EconData' s dX Data Service. In most cases the data names accord with the official names used in dX. The following lists the relevant location within dX and any transformation applied to the data. All data were seasonally adjusted and yearly data were transformed from the quarterly time series using dX's procedures.
| Prices | |
| GDP deflator | ABS TSS – Table N1 |
|---|---|
| CPI | ABS TSS – Table R1 |
| CPI-OECD | RBA Bulletin Database – Table 11 |
| Interest Rates | |
| Commercial bill rate | NIF-1OS – Table R1 |
| PAYE tax rate payable | NIF-10 – Table R2 |
| The nominal and real pre- and after-tax rate were constructed according to the formula in the paper. | |
| Taxes | |
| Gross PAYE instalments | NIF-1OS – Table T |
| Total taxes on persons | NIF-1OS – Table T |
| Wages | |
| Wages, salaries and supplements | ABS TSS – Table NQ-8 |
| Industrial disputes | ABS TSS – Table L4–3 |
| The wage share was calculated as wages, salaries and supplements divided by GDP. | |
| Cash Flows for Corporate Trading Enterprises | |
| Gross operating surplus | NTF-10S – Table Y |
| Tax payments | NIF-1OS – Table T |
| Depreciation | NIF-1OS – Table D2 |
| Stock valuation adjustment | NIF-1OS – Table K |
| Cash flow was calculated as GOS = Tax + Dep – SVA. The rate of cash flow used in the investment equations was calculated as the cash flow divided by the total capital stock. | |
| Capital Stocks and Investment | |
| Plant and equipment CTEs | NTF 10S – Table K |
| Fixed capital stock of CTEs | NTF 10S – Table K |
| Private non-farm inventory | NIF 10S – Table K |
| Gross private GFCE (plant and equipment) | NIF 10S-Table 11 |
| Investment Allowance | NIF 10S – Table K |
| The fixed capital stock of CTEs is the sum of plant and equipment plus other buildings and structures. The total capital stock of CTEs was derived by adding inventories to the fixed capital stock. Data on CTE inventories was not available and it was constructed assuming it to be 85 per cent of private non-farm inventories. | |
| The investment ratio was calculated as gross private GFCE (plant and equipment) divided by the lagged stock of plant and equipment. | |
| Production Function Data | |
| Total non-farm employment | NIF 10S – Table N |
| Average weekly hours worked | NIF 10S – Table N |
| Total hours worked is the product of total non-farm employment and average weekly hours. The capital-labour ratio is the stock of plant and equipment for CTEs divided by total hours. Output per hour is real GDP divided by total hours. | |
| In the calculation of the effect on the capital stock it was assumed that two thirds of gross investment is replacement and one third adds to the capital stock. This approximation was derived by observing that the ratio of consumption of fixed capital to gross fixed capital investment varies between 0.5 and 0.8 (see ABS TSS Table NQ-14). For much of the 1970s and 1980s, this ratio was at or near 0.66. | |
Footnotes
See York (1990) and Lipsey (1990). [1]
Hence the commonly reported fear of inflation. [2]
See also Blanchard (1990) and McCallum (1990) related surveys. [3]
Cooley and Hansen (1991) demonstrate in a general equilibrium framework that these costs double when one accounts for other distorting taxes. But they still remain small. [4]
This issue is examined in more detail below. [5]
This effect is separate from any relative price effects of reduced after-tax real wages. [6]
See Kearl (1979). [7]
Fischer (1983) considers the question of why wide-scale indexing is not usually adopted in moderate inflations. [8]
Our assumption that the LAS curve is vertical is commonplace, see Hall and Taylor (1986), though still not without some controversy, see Fair (1984) and Gordon's, comments. [9]
This begs the question of the source of the externality causing the inflation-neutral level of output to be suboptimal. Having answered that question, the appropriateness of inflation as an optimal intervention can then be addressed. [10]
That the conditional measure generally exceeds the unconditional measure results from the fact that the series of forecast errors had a non-zero mean. It is usually the case that series of forecast errors are mean-adjusted before use in further analysis. [11]
This condition is usually written r = i – π, by dropping the product term r π. [12]
A result recently disputed by Moazzami (1991) using Carmichael's and Stebbing's data. [13]
Carmichael (1990) and (1991). [14]
See Chapman (1990). [15]
See Gordon (1988) for a discussion of the ‘mark-up over wages’ model of price formation. [16]
Given the integration in the variables, it may be more appropriate to estimate a multi-equation cointegrated system. [17]
Crozier and Rahman (1988) find evidence of a negative correlation between inflation and Canadian real stock returns. However, they are unwilling to dismiss the hypothesis of Fama (1981) that such a correlation is proxying for a negative relationship between inflation and real economic activity, and thus to stocks. [18]
For more recent evidence see Altig and Carlstrom (1991). [19]
References
Alexander, W.R.J. (1990), ‘Growth: Some Combined Cross-Sectional and Time Series Evidence from OECD Countries’, Applied Economics, 22, pp. 1197–1204.
Altig, D. and C.T. Carlstrom (1991), ‘Inflation, Personal Taxes, and Real Output: A Dynamic Analysis’, Journal of Money, Credit, and Banking, 23, pp. 547–579.
Andersen, P.S. (1989), ‘Inflation and Output: A Review of the Wage-Price Mechanism’, BIS Economic Papers No. 24.
Bailey, M.J. (1956), ‘The Welfare Cost of Inflationary Finance’, Journal of Political Economy, 64, pp. 93–100.
Ball, L. (1990), ‘Why Does High Inflation Raise Inflation Uncertainty?’, NBER Working Paper No. 3224.
Ball, L. and S.G. Cecchetti (1990), ‘Inflation and Uncertainty at Short and Long Horizons’, Brookings Papers on Economic Activity, No.1, pp. 215–254.
Benge, M. (1992), ‘Taxes, Inflation and Investment in a Small Open Economy’, paper presented at the 10th Economic Theory Workshop, UNSW, February.
Blanchard, O.J. (1990), ‘Why Does Money Affect Output? A Survey’, Chapter 15 in B.M. Friedman and F.H. Hahn (eds.), Handbook of Monetary Economics, Volume II, North Holland, Amsterdam.
Blejer, M.I. and L. Leiderman (1980), ‘On the Real Effects of Inflation and Relative-Price Variability: Some Empirical Evidence’, The Review of Economics and Statistics, LXII, pp. 539–544.
Buck, A.J. and F. Fitzroy (1988), ‘Inflation and Productivity Growth in the Federal Republic of Germany’, Journal of Post Keynesian Economics, X, pp. 428–444.
Bullock, M. and M. Rider (1991), ‘The Cross-Country Relationship between Interest Rates and Inflation over Three Decades’, Reserve Bank of Australia Research Discussion Paper 9104.
Carlton, D.W. (1979), ‘Contracts, Price Rigidity, and Market Equilibrium’, Journal of Political Economy, 87, pp. 1034–1062.
Carlton, D.W. (1982), ‘The Disruptive Effect of Inflation on the Organization of Markets’, in R.E. Hall (ed.), Inflation: Causes and Effects, University of Chicago Press, Chicago.
Carmichael, J. (1990), ‘Inflation: Performance and Policy’ in S. Grenville (ed.), The Australian Macro-Economy in the 1980s, Reserve Bank of Australia, Sydney.
Carmichael, J. and N. Dews (1989), ‘Investment and Australian Economic Growth’, in B. Chapman (ed.), Australian Economic Growth, MacMillan, South Melbourne.
Carmichael, J. and P.W. Stebbing (1983), ‘Fisher's Paradox and the Theory of Interest’, The American Economic Review, 73, pp. 619–630.
Cassidy, B. (1991), ‘The Redistributive Effects of Inflation’, Treasury Research Paper No. 2, The Treasury, Canberra.
Cecchetti, S.G. (1986), ‘The Frequency of Price Adjustment: A Study of the Newsstand Prices of Magazines’, Journal of Econometrics, 31, pp. 255–274.
Chapman, B. (1990), ‘The Labour Market’, in S. Grenville (ed.), The Australian Macro-Economy in the 1980s, Reserve Bank of Australia, Sydney.
Christophides, L.N. and D.A. Wilton (1983), ‘The Determinants of Contract Length – An Empirical Analysis Based on Canadian Micro Data’, Journal of Monetary Economics, 12, pp. 309–319.
Clark, P.K. (1982), ‘Inflation and the Productivity Decline’, The American Economic Review, 72, pp. 149–154.
Cooley, T.F. and G.D. Hansen (1991), ‘The Welfare Costs of Moderate Inflations’, Journal of Money, Credit, and Banking, 23, pp. 481–518.
Cozier, B.V. and A.H. Rahman (1988), ‘Stock Returns, Inflation, and Real Activity in Canada’, Canadian Journal of Economics, XXI, pp. 759–774.
Cozier, B.V. and J.G. Selody (1992), ‘Inflation and Macroeconomic Performance: Some Cross-Country Evidence’, Department of Monetary and Financial Analysis, Bank of Canada, FR-92-003.
Crouch, C. (1985), ‘Conditions for Trade Union Restraint’, in L.N. Lindberg and C.S. Maier (eds.), The Politics of Inflation and Economic Stagnation, Brookings Institution, Washington, DC.
Cukierman, A. (1977), ‘Heterogenous Inflationary Expectations, Fisher's Theory of Interest, and the Allocative Efficiency of the Bond Market’, Economics Letters, 5, pp. 213–229.
Cukierman, A. (1984), Inflation, Stagflation, Relative Prices, and Imperfect Information, Cambridge University Press, Cambridge.
Cukierman, A. and A.H. Meltzer (1986), ‘A Theory of Ambiguity, Credibility, and Inflation under Discretion and Asymmetric Information’, Econometrica, 54, pp. 1099–1128.
Cukierman, A. and P. Wachtel (1979), ‘Differential Inflationary Expectations and the Variability of the Rate of Inflation: Theory and Evidence’, The American Economic Review, 69, pp. 595–609.
De Long, J.B. and L.H. Summers (1991), ‘Equipment Investment and Economic Growth’, The Quarterly Journal of Economics, CVI, pp. 445–502.
Domberger, S. (1987), ‘Relative Price Variability and Inflation: A Disaggregated Analysis’, Journal of Political Economy, 95, pp. 547–566.
Dombusch, R. (1988), ‘Purchasing Power Parity’, in R. Dombusch (ed.), Exchange Rates and Inflation, MIT Press, Cambridge, MA.
Dowrick, S. and D-T. Nguyen (1989), ‘OECD Comparative Growth 1950–85: Catch-Up and Convergence’, The American Economic Review, 79, pp. 1010–1030.
Driffill, J., G.E. Mizon and A. Ulph (1990), ‘Costs of Inflation’, Chapter 19 in B.M. Friedman and F.H. Hahn (eds.), Handbook of Monetary Economics, Volume II, North Holland, Amsterdam.
Eisner, R. (1989), ‘Budget Deficits: Rhetoric and Reality’, The Journal of Economic Perspectives, 3, pp. 73–94.
Engle, R.F. (1983), ‘Estimates of the Variance of US Inflation Based on the ARCH Model’, Journal of Money, Credit, and Banking, 15, pp. 286–301.
Esposito, F.F. and L. Esposito (1976), ‘Industry Price Changes, Market Structure and Inflation’, in D.A. Belsley, E.J. Kane, P.A. Samuelson and R.M. Solow (eds.), Inflation, Trade and Taxes, Ohio State University Press, Colombus.
Evans, M. (1991), ‘Discovering the Link between Inflation Rates and Inflation Uncertainty’, Journal of Money, Credit, and Banking, 23, pp. 169–184.
Fair, R.C. (1984), ‘Estimated Tradeoffs Between Unemployment and Inflation’, in Price Stability and Public Policy, A Symposium Sponsored by the Federal Reserve Bank of Kansas City, Jackson Hole, Wyoming.
Fama, E.F. (1981), ‘Stock Returns, Real Activity, Inflation, and Money’, The American Economic Review, 71, pp. 545–565.
Fane, G. (1991), ‘The Interaction between Inflation and the Taxation of Savings and Investment’, in EPAC, Australia's Inflation Problem, Office of EPAC Background Paper No. 11.
Feldstein, M. (1976), ‘Inflation, Income Taxes, and the Rate of Interest: A Theoretical Analysis’, The American Economic Review, 66, pp. 809–820.
Feldstein, M. (1980), ‘Inflation and the Stock Market’, The American Economic Review, 70, pp. 839–847.
Feldstein, M. (1982), ‘Inflation, Tax Rules and Investment’, Econometrica, 50, pp. 825–862.
Feldstein, M. (1983), Inflation, Tax Rules, and Capital Formation, University of Chicago Press, Chicago.
Feldstein, M. and J. Slemrod (1978), ‘Inflation and the Excess Taxation of Capital Gains on Corporate Stock’, National Tax Journal, 31, pp. 107–118.
Figlewski, S. and P. Wachtel (1981), ‘The Formation of Inflationary Expectations’, The Review of Economics and Statistics, LXII, pp. 1–10.
Fischer, S. (1981a), ‘Towards an Understanding of the Costs of Inflation: II’, in The Costs and Consequences of Inflation, Carnegie-Rochester Conference Series on Public Policy, 15, pp. 5–42.
Fischer, S. (1981b), ‘Relative Shocks, Relative Price Variability, and Inflation’, Brookings Papers on Economic Activity, No. 2, pp. 381–431.
Fischer, S. (1983), ‘Indexing and Inflation’, Journal of Monetary Economics, 12, pp. 519–542.
Fischer, S. (1984), ‘The Benefits of Price Stability’, in Price Stability and Public Policy, A Symposium Sponsored by the Federal Reserve Bank of Kansas City, Jackson Hole, Wyoming.
Fischer, S. and J. Huizinga (1982), ‘Inflation, Unemployment, and Public Opinion Polls’, Journal of Money, Credit, and Banking, 14, pp. 1–19.
Fischer, S. and F. Modigliani (1978), ‘Towards an Understanding of the Real Effects and Real Costs of Inflation’, Weltwirtschaftliches Archiv, 114, pp. 810–833.
Foster, E. (1978), ‘The Variability of Inflation’, The Review of Economics and Statistics, 60, pp. 346–350.
Freebairn, J. (1991), ‘Taxation and Inflation’, in EPAC, Australia's Inflation Problem, Office of EPAC Background paper No. 11.
Friedman, M. (1977), ‘Inflation and Unemployment’, Journal of Political Economy, 85, pp. 451–471.
Gordon. R.J. (1988), ‘The Role of Wages in the Inflation Process’, The American Economic Review, 78, pp. 276–282.
Grier, K.B. and G. Tullock (1989), ‘An Empirical Analysis of Cross-Sectional National Economic Growth, 1951–80’, Journal of Monetary Economics, 24, pp. 259–276.
Grimes. A. (1990), ‘The Effects of Inflation on Growth – Some International Evidence’, Weltwirtschaftliches Archiv, 127, pp. 631–644.
Gruen, D.W.R. (1991), ‘The Effect of Steady Inflation on Interest Rates and the Real Exchange Rate in a World with Free Capital Flows’, Reserve Bank of Australia Research Discussion Paper 9101.
Hall, R.E. (1982), Inflation: Causes and Effects, University of Chicago Press, Chicago.
Hall, R.E. and J.B. Taylor (1986), Macroeconomics: Theory, Performance, and Policy, W.W. Norton, New York.
Hartman, R. (1991), ‘Relative Price Variability and Inflation’, Journal of Money, Credit, and Banking, 23, pp. 185–205.
Hirsch, B.T. and J.T. Addison (1986), The Economic Analysis of Unions: New Approaches and Evidence, Hyman, London.
Howitt, P. (1990), ‘Zero Inflation as a Long-Term Target for Monetary Policy’, in R.G. Lipsey (ed.), Zero Inflation: The Goal of Price Stability, Policy Study 8, C.D. Howe Institute, Ottawa.
Hughes, H. (1989), Australian Exports: Performance, Obstacles and Issues of Assistance, Report of the Committee for Review of Export Market Development Assistance, AGPS, Canberra.
Jarrett, P.J. and J.G. Selody (1982), ‘The Productivity-Inflation Nexus in Canada, 1963–1979’, The Review of Economics and Statistics, LXIV, pp. 361–363.
Jonson, P.D. (1990), ‘Inflation: Its Costs, Its Causes and Its Cure’, Policy, Winter, pp. 2–8.
Jump, G.V. (1980), ‘Interest Rates, Inflation Expectations, and Spurious Elements in Measured Real Income and Saving’, The American Economic Review, 70, pp. 990–1004.
Kearl, J.R. (1979), ‘Inflation, Mortgages, and Housing’, Journal of Political Economy, 87, pp. 1115–1138.
Kent, C. and P. Scott (1991), ‘The Direction of Australian Investment from 1985/86 to 1988/89’, Reserve Bank of Australia Research Discussion Paper 9106.
Kormendi, R.C. and P.G. Meguire (1985), ‘Macroeconomic Determinants of Growth: Cross Country Evidence’, Journal of Monetary Economics, 16, pp. 141–163.
Krugman, P.R. (1989), Exchange-Rate Instability, MIT Press, Cambridge, MA.
Kydland, F.E. and E.C. Prescott (1980), ‘A Competitive Theory of Fluctuations and the Feasibility and Desirability of Stabilization Policy’, in S. Fischer (ed.), Rational Expectations and Public Policy, University of Chicago Press, Chicago.
Kyriakopoulos, J. (1990), ‘Does Moderate Inflation Affect Growth?’, mimeo., Research Department, Reserve Bank of Australia.
Laidler, D.E. (1978), ‘The Welfare Costs of Inflation in Neoclassical Theory – Some Unsettled Questions’, in E. Lundbert (ed.), Inflation Theory and Anti-Inflation Policy, MacMillan Press, London.
Laidler, D.E. and M.J. Parkin (1975), ‘Inflation: A Survey’, Economic Journal, 85, pp.741–809.
Leijonhufvud, A. (1981), ‘Costs and Consequences of Inflation’, in A. Leijonhufvud (ed.), Information and Coordination Essays in Macroeconomic Theory, Oxford University Press, New York.
Levi, M.D. and J.H. Makin (1978), ‘Anticipated Inflation and Interest Rates: Further Interpretation of Findings on the Fisher Equation’, The American Economic Review, 68, pp. 801–812.
Levi, M.D. and J.H. Makin (1980), ‘Inflation Uncertainty and the Phillips Curve: Some Empirical Evidence’, The American Economic Review, 70, pp. 1022–1027.
Lipsey, R.G. (1990), ‘The Political Economy of Inflation Control’, in R.G. Lipsey (ed.), Zero Inflation: The Goal of Price Stability, Policy Study 8, CD. Howe Institute, Ottawa.
Logue, D.E. and R.J. Sweeney (1981), ‘Inflation and Real Growth: Some Empirical Results’, Journal of Money, Credit, and Banking, 13, pp. 497–501.
Logue, D.E. and T.D. Willet (1976), ‘A Note on the Relation between the Rate and Variability of Inflation’, Economica, 43, pp. 151–158.
Lowe, P. (1992), ‘The Term Structure of Interest Rates, Real Activity and Inflation’, Reserve Bank of Australia Research Discussion Paper 9204.
Lucas, R.E. (1972), ‘Expectations and the Neutrality of Money’, Journal of Economic Theory, 4, pp. 103–124.
Lucas, R.E. (1973), ‘Some International Evidence on Output-Inflation Tradeoffs’, The American Economic Review, 63, pp. 526–534.
Macfarlane, I.J. (1989), ‘Money, Credit and the Demand for Debt’, Reserve Bank of Australia Bulletin, May, pp. 21–31.
Macfarlane, I.J. (1990), ‘Credit and Debt: Part II’, Reserve Bank of Australia Bulletin, May, pp. 27–35.
Macfarlane, I.J. and W.J. Tease (1989), ‘Capital Flows and Exchange Rate Determination’, Reserve Bank of Australia Research Discussion Paper 8908.
Makin, J.H. (1983), ‘Anticipated Money, Inflation Uncertainty and Real Economic Activity’, The Review of Economics and Statistics, 65, pp. 126–134.
Makin, T. (1990), ‘The Real Federal Budget Imbalance’, The Economic Record, 66, pp. 249–253.
McCallum, B.T. (1990), ‘Inflation: Theory and Evidence’, Chapter 18 in B.M. Friedman and F.H. Hahn (ed.), Handbook of Monetary Economics, Volume II, North Holland, Amsterdam.
Mehra, Y.P. (1991), ‘Wage Growth and the Inflation Process: An Empirical Note’, The American Economic Review, 81, pp. 931–937.
Mizon, G.E. (1991), ‘Modelling Relative Price Variability and Aggregate Inflation in the United Kingdom’, Scandinavian Journal of Economics, 93, pp. 189–211.
Moazzami, B. (1991), ‘The Fisher Equation Controversy Re-examined’, Applied Financial Economics, 1, pp. 129–133.
Mullineaux, D.J. (1980), ‘Unemployment, Industrial Production, and Inflation Uncertainty in the United States’, The Review of Economics and Statistics, LXII, pp. 163–169.
Nickell, S. (1990), ‘Inflation and the UK Labour Market’, Oxford Review of Economic Policy, 6, pp. 26–35.
Novin, F. (1991), ‘The Productivity-Inflation Nexus Revisited: Canada, 1969–1988’, Working Paper 91-1, Research Department, Bank of Canada.
Nowotny, E. (1980), ‘Inflation and Taxation: Reviewing the Macroeconomic Issues’, The Journal of Economic Literature, XVIII, pp. 1025–1049.
Okun, A.M. (1971), ‘The Mirage of Steady Inflation’, Brookings Papers on Economic Activity, No. 2, pp. 485–498.
Okun, A.M. (1975), ‘Inflation: Its Mechanics and Welfare Costs’, Brookings Papers on Economic Activity, No. 2, pp. 351–401.
Orphanides, A. and R.M. Solow (1990), ‘Money, Inflation and Growth’, Chapter 6 in B.M. Friedman and F.H. Hahn (eds.), Handbook of Monetary Economics, Volume II, North Holland, Amsterdam.
Pagan, A.R. and M.R. Gray (1983), ‘Inflation and Investment – An Historical Overview’, in A.R Pagan and P.K. Trivedi (eds.), The Effects of Inflation: Theoretical Issues and Australian Evidence, Centre for Economic Policy Research, Australian National University, Canberra.
Pagan, A.R., A.D. Hall and P.K. Trivedi (1983), ‘Assessing the Variability of Inflation’, Review of Economic Studies, L, pp. 585–596.
Pagan, A.R. and P.K. Trivedi (1983), ‘The Effects of Inflation: A Review with Special Reference to Australia’ in A.R. Pagan and P.K. Tivedi (eds.), The Effects of Inflation: Theoretical Issues and Australian Evidence, Centre for Economic Policy Research, Australian National University, Canberra.
Parkin, M. (1986), ‘The Output-Inflation Trade-off When Prices are Costly to Change’, Journal of Political Economy, 94, pp. 200–224.
Parkinson, M. (1991), ‘Inflation and Uncertainty’, Treasury Research Paper No. 3, The Treasury, Canberra.
Parks, R.W. (1978), ‘Infration and Relative price Variability’, Journal of Political Economy, 86, pp. 79–85.
Paroush, J. (1986), ‘Inflation, Search Costs and Price Dispersion’, Journal of Macroeconomics, 8, pp. 329–336.
Russell, B. and W. Tease (1990), ‘Employment, Output and Real Wages’, The Economic Record, 66, pp. 34–43.
Ryan, C.J. (1990), ‘Inflation and Corporate Taxation in Australia’, Reserve Bank of Australia Research Discussion Paper 9011.
Sheshinski, E. and Y. Weiss (1983), ‘Inflation and Costs of Price Adjustment’, Review of Economic Studies, 50, pp. 287–303.
Siebert, W.S. and J.T. Addison (1981), ‘Are Strikes Accidental?’, Economic Journal, 91, pp. 389–404.
Silvapulle, P. and B. Inder (1992), ‘Does the Fisher Effect Apply in Australia?’, Department of Economics, La Trobe University Discussion Paper 2/92.
Summers, L.H. (1983), ‘The Nonadjustment of Nominal Interest Rates: A Study of the Fisher Effect’, in J. Tobin (ed.), Macroeconomics, Prices and Quantities, Brookings Institution, Washington, DC.
Taylor, J.B. (1981), ‘On the Relation between the Variability of Inflation and the Average Inflation Rate’, in The Costs and Consequences of Inflation, Carnegie-Rochester Conference Series on Public Policy, 15, pp. 5–42.
Urbanski, T. (1990), ‘Asset Price Inflation’, Treasury Research Paper No.1, The Treasury, Canberra.
Vann, R.J. and D.A. Dixon (1990), Measuring Income Under Inflation, Research Study No. 12, Australian Tax Research Foundation.
Vining, D.R. and C. Eltertowski (1976), ‘The Relationship Between Relative Prices and the General Price Level’, The American Economic Review, 66, pp. 699–708.
Willmann, H. (1990), ‘Some Calculations on Inflation and Corporate Taxation in Australia’, Reserve Bank of Australia Research Discussion Paper 9012.
York, R.C. (ed.) (1990), Taking Aim: The Debate on Zero Inflation, Policy Study 10, C.D. Howe Institute, Ottawa.