Reform of Credit Card Schemes in Australia: II Commissioned Report 9. Technical Appendix
Download the complete Report 373KB
- This appendix reviews several economic models that have been developed to examine issues relevant to the Joint Study. It also analyses two simple alternative models that highlight the importance of various assumptions made in the existing literature.
A. Common Notation
- The various papers discussed here generally follow similar notational conventions. Table 1 summarizes that notation as used in the present report. In some cases, the notation used in the original analyses has been translated to create uniform conventions for the discussion below.
| Transactions Benefits of Card Use | ||
|---|---|---|
| bb | = | per-transaction benefits enjoyed by a buyer when using a credit or charge card to make a purchase in comparison with using the next-best payment mechanism |
| G(b) | = | percentage of consumer population for whom bb = b |
| bm | = | per-transaction benefits enjoyed by a merchant from card use in comparison with the next-best payment mechanism[169] |
| Costs | ||
| cI | = | cost incurred by card issuers on a per-transaction basis |
| cF | = | annual fixed cost per account incurred by an issuer |
| cA | = | cost incurred by merchant acquirers on a per-transaction basis |
| Fees and Charges | ||
| f | = | annual charge levied by issuers on cardholders |
| f*(c) | = | equilibrium annual charge levied by issuers when they have net marginal costs c |
| r | = | rebate paid by issuers to cardholders on a per-transaction basis |
| m | = | merchant service fee charged on a per-transaction basis |
| m*(c) | = | equilibrium transaction charge levied by acquirers when they have net marginal costs c |
| a | = | interchange fee paid by acquirer to the issuer |
| Retail Prices and Consumer Willingness to Pay for the Goods | ||
| v | = | dollar value consumer is willing to pay for a unit of a retailer's output not accounting for any disutility associated with that merchant or from using other than the consumer's preferred payment mechanism |
| pcr | = | price charged by the merchant for a credit or charge card-based transaction |
| pca | = | price charged by the merchant for a non-card-based (‘cash’) transaction |
B. ‘Cooperation Among Competitors: The Economics of Payment Card Associations’ by Jean-Charles Rochet and Jean Tirole
- Professors Rochet and Tirole develop a formal model in which they examine the effects of interchange rates and a no-surcharge rule.[170] The bulk of their analysis concerns an economy with a single credit card network and a single alternative payment mechanism, cash. They assume that acquiring is competitive and consider a variety of market structures for issuing. Merchants are assumed to be differentiated price setters along the lines of the standard Hotelling model with fixed locations. The timing of their model is as follows (1) the interchange fee is set; (2) issuers set customer fees and customers make cardholding choices, while merchants make card acceptance decisions and then set their retail prices; and (3) customers make retail purchases.[171] Their basic model assumes that any consumer who obtains a credit card makes a fixed number of transactions (normalized to one) so that there is no distinction between annual fees and transactions charges in their model.[172]
- As expected, Rochet and Tirole find that, when there is frictionless surcharging, the interchange fee has no effects on equilibrium card use or the net prices faced by consumers.[173] The welfare properties of the frictionless surcharging case depend on the degree of issuer competition. First, suppose issuers are perfectly competitive. Perfectly competitive issuers set f = cI − a. Given that acquirers are perfectly competitive, they set the merchant service fee equal to the marginal cost of acquisition: m = cA+a. Under the symmetric Hotelling model, merchants pass through marginal cost differences on a one-for-one basis, so the surcharge is equal to the merchant's net benefits (costs) of card use. That is, merchants set the card surcharge equal to the merchant service fee minus the merchants' transactions benefits, or Pcr − P = cA + a − bm, which can be positive or negative. Hence, the net cost of a card transaction to the consumer is f + Pcr − P = cA + a − bm, which provides the consumer incentives to make the efficient choice. When issuers are perfectly competitive, the surcharging equilibrium leads to efficient card use and the consumption of retail goods: Merchant surcharges fully internalize what could otherwise have been externalities.
- When issuers are less than perfectly competitive, so that f*(c)>c, the surcharge equilibrium entails too little card use because now f + Pcr − Pca > cI + cA − bm. This distortion is not due to the failure to internalize network effects or other externalities. Instead, the problem is the exercise of issuer market power.
- The interchange fee can affect the equilibrium outcome in the Rochet-Tirole model when a no-surcharge rule is in effect. Rochet and Tirole find that an ‘issuer-controlled’ association may choose an interchange fee that leads to ‘overprovision’ of credit card services.[174] In other cases, both the privately and socially optimal interchange fees are equal to the highest level consistent with merchant acceptance of cards. Although Rochet and Tirole do not derive this result, it can be shown that, for sufficiently competitive issuers, the privately optimal interchange fee is greater than the socially optimal one.[175]
- Having characterized the equilibrium with and without a no-surcharge rule, Rochet and Tirole examine the net effects of the rule and find that it may raise or lower welfare.[176] Rochet and Tirole also find that:(a) in comparison with charging solely per-transaction fees, charging cardholders annual fees as well as per-transactions fees can weaken ‘merchant resistance’ to accepting cards when the interchange fee exceeds issuer cost,[177] and (b) ‘lifting the nosurcharge…’.[178]
- Like those of any model, the results of the Rochet-Tirole model are sensitive to the assumptions made. For example, the model makes an assumption that eliminates another type of distortion that would be expected in practice. With a no-surcharge rule in effect, consumers in the Rochet-Tirole model who do not use credit cards end up paying higher prices than they would if surcharging were allowed or if credit cards were banned. Moreover, even when surcharging is feasible, the prices for non-card transactions are set above marginal costs. A nosurcharge rule increases this margin. In the Rochet and Tirole model, however, consumer demands are unresponsive to prices over the relevant range, and there are no adverse allocative efficiency effects from this price distortion. In more realistic settings, where consumers reduce consumption in response to higher prices, the increased margins will give rise to efficiency losses.[179]
- Rochet and Tirole also assume that acquiring is perfectly competitive. If it is not, then the highest interchange fee consistent with merchant acceptance can be lower than indicated in their baseline model. Let m*(cA+a) denote the merchant fee charged by acquirers given costs cA and interchange fee a. Then the condition for merchant acceptance is m*(cA+a)≤ E[bb | bb ≥ f*(cI − a] + bm. Stated differently, increased acquirer competition that shifts m* downward will lead to greater net incentives for merchant acceptance, all else equal.
- Lastly, Rochet and Tirole also make specific assumptions about the nature of merchant competition. Under the symmetric Hotelling duopoly model, merchants pass through marginal cost differences on a one-for-one basis, so the surcharge is equal to the merchant's net benefits (costs) of card use. Under other models of merchant behavior, surcharges might fail to be set at efficient levels even if both acquiring and issuing were perfectly competitive.
C. ‘An Economic Analysis Of A Card Payment Network’ by Julian Wright
- Dr. Wright examines a modified version of the Rochet and Tirole model to analyse the economic effects of a no-surcharge rule and the setting of an interchange fee. He examines a variety of different retail market structures and reaches very different conclusions than do Rochet and Tirole. Unlike Rochet and Tirole, he allows for increased-sales benefits at the economywide level–with some probability a consumer can make a purchase only if he or she holds a card and the merchant accepts the card.[180]
- By their nature, models are often built on unrealistic or stylized assumptions, and one must test whether the results are plausible. In the Wright model, one assumption is particularly unrealistic and troubling. Specifically, the model assumes that consumers purchase a fixed number of goods each period as long as the price is less than a single reservation price that is the same for all consumers.[181] This assumption gives rise to several potentially misleading conclusions. First, as noted above in the discussion of Rochet and Tirole's model, this assumption de facto eliminates the possibility of efficiency losses from distortions in the purchase behavior of non-cardholders induced by excessively high (or low) retail prices for goods and services. Second, this assumption is the reason that the model exhibits the property that surcharging eliminates the use of credit cards when merchants have monopoly power. The common willingness to pay allows that merchant to extract all of a consumer's incremental surplus from making a card-based purchase.
- To see the power of this assumption (and the unreasonableness of its implications), suppose that all consumers have the same willingness to pay for a good and must incur a fixed cost to get to the merchant, regardless of the method of payment used. Once the consumer has sunk the cost of getting to the merchant, the merchant should charge a price that extracts all of the surplus of the marginal consumer. But then that consumer would regret having gone to the store and, recognizing that this is what will happen, would never have gone in the first place. Thus, if there are any costs of going to a store, there can be no shopping!
- Different and more realistic assumptions would give rise to different results. For example, if it is assumed that consumers continuously reduce their purchase quantities in response to higher merchant prices, then it can be unprofitable for merchants to extract all of a consumer's surplus through higher prices. A simple model of this type is examined in Part IX.F below. Another example is a model in which a given consumer has different values of bb for different transactions.
- A final point with respect to the analysis is that the model apparently takes the levels of fixed annual charges to be exogenous. In fact, these levels are endogenous and, in practice, they vary across cards. This assumption can be significant because rate structures, as well as levels, matter for consumers' incentives to hold and use cards. For example, the conclusions of the analysis would change if the fixed charges to cardholders were set at 0, as is done by some cards in Australia. In this case, it would be an equilibrium outcome for all consumers in the model to hold cards, regardless of merchant pricing strategies. Thus, results indicating that too few consumers hold cards would no longer apply.
- Dr. Wright also presents the results of a simulation model. One problem with these simulations is that they build on models embodying the unrealistic assumptions discussed above. A second problem is that there is almost no documentation of the sources of the various parameter values used in the simulations, and thus it is difficult to judge their validity.[182]
- For example, the welfare calculations appear to be based on the assumption that there are 15 million unique credit card holders. If so, this is an overestimate. The total number of adults in Australia in December 2000 was 15.3 million, and many of them apparently do not have a credit card.[183] In June 2001, the Reserve Bank of Australia estimated that there were 9.6 million credit card accounts.[184] Survey data collected by the Australian Payments Clearing Association indicate that there are 12.1 million credit cards on issue.[185] Even if each cardholder has only one card, and even if the number of American Express and Diners Club cards are added (though it is not clear that this is Wright's intent) the number of credit cardholders appears to be significantly less than 15 million.[186] To the extent that some cardholders hold more than one card, the number of unique cardholders would be even smaller.
D. ‘Same Price, Cash or Credit: Vertical Control by Payment Networks’ by Marius Schwartz and Daniel R. Vincent.
- Professors Schwartz and Vincent examine the effects of interchange rates and a nosurcharge rule.[187] Their model assumes away consumer cardholding decisions: One fixed set of consumers always uses credit cards when they make purchases and another fixed set of consumers always uses cash. Instead of modeling cardholding decisions, the authors allow for consumers to adjust their purchase levels in response to retail prices and the analysis focuses on the welfare effects of changes in net retail prices. The model is complementary to that of Rochet and Tirole in the sense that each model examines an effect assumed away by the other.
- The authors examine two models, one that they interpret as a closed credit card system and one that they interpret as an open credit card system or association. The authors conclude that a no-surcharge rule may raise or lower total surplus.[188] For the case of an open system (their competitive issuers case), Schwartz and Vincent find that a no-surcharge rule lowers total surplus when consumers' demand functions for the merchant's product are linear and bm = 0.[189] Imposition of a no-surcharge rule raises the net price paid by non-card users and lowers the net price paid by card users. Under the assumptions of their model, the welfare losses outweigh the gains.[190]
E. ‘Regulating Interchange Fees In Payment Systems" by Joshua S.Gans and Stephen P.King
- Professors Gans and King examine the welfare effects of a no-surcharge rule and characterize the socially optimal interchange fee level.[191] They use a special formulation of demand, which leads to strong results. Specifically, Gans and King assume that a consumer makes all of his or her purchases from a single merchant and credit card use raises a consumer's willingness to pay for the retail good, but does so by an amount that decreases with the volume of card use. This structure allows the merchant to charge separately for card use and thus price discriminate against card use. Moreover, given the model's formulation of demand, all marginal purchases are made using cash. Hence, changes in the credit card price affect only the extent to which credit cards are used and have no effect on total purchase volume. Thus, the cash price with surcharging is identical to the common price under a no-surcharge rule.[192] In this model, non-card users are no worse off under the no-surcharge rule.
- These results do not appear to be robust. As already discussed, imposition of a nosurcharge rule often raises the price paid by non-card users. Furthermore, price discrimination against card use need not occur under the alternative model presented in the next part of this section. This result also need not extend to the case of multiple merchants, even where each merchant is a monopoly supplier in a separate product market. To see this point, consider a three-sector economy. Two of the sectors are monopolized. That is, there is a single producer of the product sold in each of these markets. There is also a cash-only sector of the economy that offers an unlimited number of constant surplus transactions, where the surplus is normalized to zero. Although each firm monopolizes the supply of its product, the two retailers compete to attract card use. As Bertrand competitors, they will drive the retail ‘price for card use,’ pcr - pca down to m − bm. Hence, with competitive acquirers and no interchange fee, there will be no price discrimination against card users and surcharging will fully internalize what might otherwise be external effects. Of course, each retailer's overall monopoly markup over marginal cost will remain, but this will not distort the marginal choice of payment mechanisms.
F. An Alternative Model Of Comsumer Demand
- This part presents an illustrative analysis of a model that extends Professors Schwartz and Vincent's model of consumer behavior to allow for endogenous cardholding decisions. This model demonstrates that, contrary to the findings of Professors Gans and King, a monopoly merchant may choose not to price discriminate against card use when surcharging is allowed. This model also sheds light on Dr. Wright's prediction that frictionless surcharging will destroy the market for credit and charge cards and demonstrates one of the reasons why this prediction is almost certainly incorrect.
- As in the baseline versions of the other models summarized in this appendix,
consider an economy with a single credit card network and a single alternative
payment mechanism, ‘cash.’ Suppose that each consumer has a downward
sloping demand curve, D(.), for a product sold by a monopoly merchant. With
probability
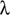 i
consumer i will need to use a credit card to make
a purchase from the merchant. If a consumer needs to use a card but the merchant
does not accept cards or the consumer does not hold one, then the consumer
makes no purchase from that merchant and instead makes a purchase in a cash-only
competitive sector of the economy that yields constant consumer and producer
surplus normalized to zero. At the time of making the decision whether to
hold a card, each consumer knows his or her probability of needing a card.
To keep the model simple, assume bb = 0 for all
consumers.[193]
i
consumer i will need to use a credit card to make
a purchase from the merchant. If a consumer needs to use a card but the merchant
does not accept cards or the consumer does not hold one, then the consumer
makes no purchase from that merchant and instead makes a purchase in a cash-only
competitive sector of the economy that yields constant consumer and producer
surplus normalized to zero. At the time of making the decision whether to
hold a card, each consumer knows his or her probability of needing a card.
To keep the model simple, assume bb = 0 for all
consumers.[193]
- Assume that acquiring and issuing are perfectly competitive, so that m = cA + a,f = cF, and r = a − cI. In what follows, observe that as in the Wright model – and in – the annual fee and rebate do not collapse to a single fee.
- The game proceeds as follows. Consumers form expectations about retail prices and then choose whether to join the credit card network by paying an annual fee of f. At the time the cardholding decision is made, consumers know the value of r, the per-transaction rebate paid by the issuer. After cardholders have signed up, the merchant chooses its prices for cashand credit card-based transactions knowing the extent of consumer cardholding. Consumers then make purchases. The equilibrium concept is that of subgame-perfect Nash equilibrium, which rules out incredible threats and promises by the merchant or consumers. In equilibrium, consumers' beliefs about retail prices at the time of making cardholding decisions are fulfilled by the actual prices the merchant charges.
-
Suppose that surcharging is allowed and consumers expect prices Pcr and Pca, where Pcr − r ≥ Pca. Given these prices, a cardholding consumer would use cash when feasible and thus a cardholding consumer enjoys expected surplus
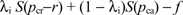
where
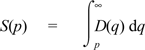
That is, S(p) is a consumer's surplus when the merchant's net price is p and he or she purchases the good. A consumer who does not hold a card enjoys expected surplus
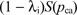
Hence, a consumer will hold a card if and only if
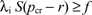 (1)
(1)
- Before continuing, observe that, given r ≤ a − cI m
≥ cA + a , and cA + cI
− bm > 0, the merchant would never choose prices
that induce full-time use of cards. The reason is that
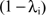 of the time, consumer i, enjoys
no transactions benefits of card use, other than the rebate. But the merchant
funds the rebate out of the merchant service fee. The merchant can increase
its profits by a setting a cash price ‘just below’ pcr
− r to induce consumers to use cash when possible and thus
allow the merchant and consumer to avoid the net card transactions costs cA
+ cI - bm. It is readily shown that this will
increase merchant profits in comparison with all consumers' using cards.
Likewise, it is never in the merchant's interest to set pcr so high that
it chokes off card use conditional on at least some consumers' holding
cards.
of the time, consumer i, enjoys
no transactions benefits of card use, other than the rebate. But the merchant
funds the rebate out of the merchant service fee. The merchant can increase
its profits by a setting a cash price ‘just below’ pcr
− r to induce consumers to use cash when possible and thus
allow the merchant and consumer to avoid the net card transactions costs cA
+ cI - bm. It is readily shown that this will
increase merchant profits in comparison with all consumers' using cards.
Likewise, it is never in the merchant's interest to set pcr so high that
it chokes off card use conditional on at least some consumers' holding
cards. - Let
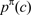 denote the profit-maximizing price
for a monopoly merchant with marginal cost c facing demand curve D(.). Normalize
demand so that the cost of cash sales is zero and the net cost of card sales
is m - bm. Then the merchant sets prices satisfying
denote the profit-maximizing price
for a monopoly merchant with marginal cost c facing demand curve D(.). Normalize
demand so that the cost of cash sales is zero and the net cost of card sales
is m - bm. Then the merchant sets prices satisfying
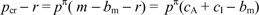 and
and
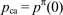 , where use has been made of
the assumption that issuers and acquirers are perfectly
competitive.[194]
Notice that the equilibrium value of
pcr - r is greater than the equilibrium value
of pca because
, where use has been made of
the assumption that issuers and acquirers are perfectly
competitive.[194]
Notice that the equilibrium value of
pcr - r is greater than the equilibrium value
of pca because
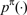 is an increasing function.
is an increasing function. - With linear demand curves of the form
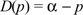 , the resulting prices are
, the resulting prices are 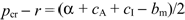 and
and 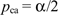 . In this case,
. In this case,
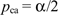 . Assuming that (cA
+ cI − bm) > 0, the merchant's
prices entail price discrimination in favor of card users because the difference
in social costs is (cA + cI −
bm). This result stands in contrast to the one obtained
by Professors Gans and King indicating that merchant pricing distorts card
use
downward.[195]
. Assuming that (cA
+ cI − bm) > 0, the merchant's
prices entail price discrimination in favor of card users because the difference
in social costs is (cA + cI −
bm). This result stands in contrast to the one obtained
by Professors Gans and King indicating that merchant pricing distorts card
use
downward.[195] -
Now consider equilibrium cardholding. Substituting the equilibrium values of relevant prices and fees into inequality (1), a consumer will hold a card if and only if
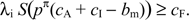
Given the merchant's prices, it is socially optimal for a consumer to hold a card if and only if
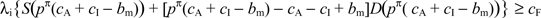
Given that
 (or else the merchant would shut
down), there is too little cardholding, conditional on the merchant's
prices. This result obtains because the cardholder ignores the positive effects
of cardholding on other economic agents; absent cardholding, the economy
forgoes sales with positive
margins.[196]
This distortion is not due to the failure to internalize network effects.
Instead, it is a monopoly commitment problem. If the merchant could commit
to a lower price for card use–and thus encourage greater cardholding–the
merchant would find it profitable to do
so.[197]
(or else the merchant would shut
down), there is too little cardholding, conditional on the merchant's
prices. This result obtains because the cardholder ignores the positive effects
of cardholding on other economic agents; absent cardholding, the economy
forgoes sales with positive
margins.[196]
This distortion is not due to the failure to internalize network effects.
Instead, it is a monopoly commitment problem. If the merchant could commit
to a lower price for card use–and thus encourage greater cardholding–the
merchant would find it profitable to do
so.[197]
-
To gain further insight, suppose that everyone has the same value of
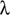 . As long as
. As long as
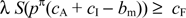 (2)
(2)
all consumers will hold cards. In contrast to Dr. Wright's finding, the market for credit cards is not destroyed even when the merchant knows the marginal consumer's valuation of credit card holding. The reason is that raising the retail price of purchases made using cards leads to a reduction in purchase levels so that it is not profitable for the merchant to raise prices to the point that the marginal cardholder enjoys no surplus.[198]
-
Now, suppose that a no-surcharge rule is put in to effect. If the interchange fee exceeds issuers' marginal costs, then issuers pay rebates to card users: For any a > cI, r > 0. In this case, any consumer holding a card would always use his or her card to make purchases. Faced with a common retail price, p, all consumers will hold cards as long as
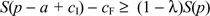 ,
(3)
,
(3)
where use has been made of the facts that the equilibrium value of r is a - cI and the equilibrium value of f is cF. If the merchant expects all of its customers to use cards, it will set its price to maximize
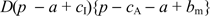 ,
,
where use has been made of the fact that the equilibrium value of m is cA + a. Knowing this, the merchant would set its retail price to satisfy
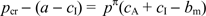 ,
,
and would earn profits of
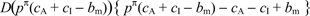 ,
,
if it accepted cards. Given the merchant's price, inequality (2) is a sufficient condition for inequality (3) to hold. Assume that inequality (2) is satisfied. If the merchant refuses to accept cards, it sets
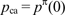 and earns profits of
and earns profits of
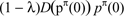 .
.
- For
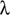 large enough, card acceptance is
an equilibrium outcome under a no-surcharge rule. As long as
large enough, card acceptance is
an equilibrium outcome under a no-surcharge rule. As long as 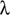 < 1, this outcome leads to excessive
card use in this model. In order to get the rebate of r, consumers
use their cards to make all of their purchases. Thus, (1 -
< 1, this outcome leads to excessive
card use in this model. In order to get the rebate of r, consumers
use their cards to make all of their purchases. Thus, (1 - 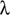 ) of the purchases are made using
cards even though there are no direct consumer benefits of card use but there
are transactions costs of
cA + cI − bm
> 0.
) of the purchases are made using
cards even though there are no direct consumer benefits of card use but there
are transactions costs of
cA + cI − bm
> 0.
G. ‘Payment Systems And Interchange Fees’ by Richard Schmalensee
- This paper examines and compares privately and socially optimal interchange fees.[199] Professor Schmalensee concludes that, in apparently non-pathological cases, the privately optimal interchange fee performs well. As noted in Part VI.B of the text above, a fundamental weakness of Schmalensee's analysis is that it uses a suspect and potentially misleading measure of economic welfare to determine the socially optimal interchange fee.[200] The problem comes from equating an individual merchant's acceptance incentives with the aggregate effect on merchant welfare. Put another way, Professor Schmalensee fails to account for the negative effects that one merchant's acceptance of credit and charge cards may have on other merchants. Thus, his model may be valid if every merchant that accepts cards is a monopolist in a separate market, but is very likely incorrect otherwise.
-
The following formal example, based on the Rochet and Tirole model, demonstrates the flaw in Schmalensee's analysis. Recall that each consumer in the Rochet-Tirole model purchases one unit of a merchant's output. Under a no-surcharge rule, a consumer makes his or her card holding and use decision by comparing the direct benefits of card use, bb, with the annual fee, f. As Rochet and Tirole show, the socially optimal interchange fee is the one that maximizes
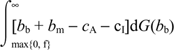 (4)[201]
(4)[201]
Note that the lower limit of integration is restricted to being non-negative, because a cardholder with a negative value of bb would never use his or her card to make a purchase. Using the fact that f = f*(cI − a), setting the derivative of (4) with respect to a equal to 0 yields the first-order condition for the socially optimal interchange fee:
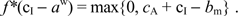 (5)
(5)
-
Under the Schmalensee approach, one would substitute merchant willingness to pay for card acceptance in place of merchant transactions benefits in the measure of total welfare. As shown by Rochet and Tirole, each merchant is willing to pay up to
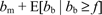 to accept cards. Thus,
the Schmalensee-optimal card fee is the one that maximizes
to accept cards. Thus,
the Schmalensee-optimal card fee is the one that maximizes
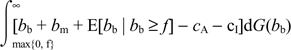
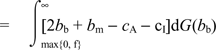 ,
,
where the equality follows from the fact that
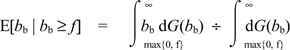 ,
,
- Comparing (4) and (6), one sees that the Schmalensee approach leads to the double counting of consumer benefits from card use: 2bb appears in the Schmalensee measure when the correct term is bb. Intuitively, because of the increased-sales effect, a merchant is willing to pay a merchant service fee up to the average level of consumer transactions benefits. Hence, by counting the increased sales effect, the consumer transactions benefits are double counted – once for consumers and once for merchants. But the increased-sales effect is not a social benefit (one merchant gains at the other's expense), so the consumer benefits should be counted only once.
-
As expected, the mismeasurement of welfare leads to calculation of the wrong value of the interchange fee. To see this fact, set the derivative of (6) equal to zero, which yields the first-order condition for the Schmalensee-optimal interchange fee:
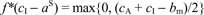 .
(7)
.
(7)
Comparing the expressions for optimal interchange fees, (5) and (7), one observes that
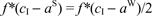 .
.
In the case of perfectly competitive issuers,
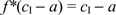 , and thus
, and thus 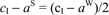 . It follows that
. It follows that
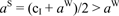
because
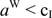 to avoid negative f. Hence,
the Schmalensee approach errs toward interchange fees that encourage excessive
card use.
to avoid negative f. Hence,
the Schmalensee approach errs toward interchange fees that encourage excessive
card use.
Footnotes
The models reviewed and analysed in this appendix assume that the “next-best” mechanism is the same for all merchants and consumers. [169]
Rochet and Tirole. [170]
Rochet and Tirole at 11. [171]
As will become clear from the discussion of Analysis of a Payment Network below, the lack of distinction between the effects of f and r also depends on the nature of merchant competition. [172]
Rochet and Tirole at 19. [173]
Rochet and Tirole Proposition 3 at 17. [174]
This conclusion follows from the fact that, as the issuer margin goes to zero, the socially optimal interchange fee goes to bm − cA, which results in a merchant service fee of m = bm, which in turn is lower than a merchant's cutoff value for accepting cards because the latter includes the private increased-sales benefits. [175]
Rochet and Tirole Proposition 4 at 20. [176]
Rochet and Tirole Proposition 1' at 23. [177]
Rochet and Tirole at 20. [178]
Of course, one would also have to take into account that a no-surcharge rule may reduce distortions in card-user consumption levels. Schwartz and Vincent offers an analysis of how these effects balance and establishes conditions under which the adverse effects outweigh the beneficial ones. [179]
The implications of, and difficulties with, this assumption were discussed earlier in Part V.B above. [180]
Analysis of a Payment Network , Assumption (A1) at 7. [181]
Analysis of a Payment Network at 34 and 35. [182]
Of a population of 19.277 million Australians in December 2000, 79.5 percent, or 15.3 million, were aged 15 or older. Data provided by Reserve Bank of Australia. [183]
This figure includes only bank issued credit cards. (Reserve Bank of Australia, ‘C1: Credit Card Statistics – Banks,’ https://www.rba.gov.au/Statistics/Bulletin/C01hist.xls (site visited August 25, 2001).) [184]
Data provided by Reserve Bank of Australia. This is consistent with other estimates that, on average, there are 1.3 cardholders for every account. See Mike Macrow, Craig Williams, and Alistair Scarff, ‘Credit Cards, An Ace Up the Sleeve,’ Merrill Lynch, 14 April 2000, at 18. [185]
Merrill Lynch estimated that American Express had 1 million and Diners Club had 600,000 cards on issue in Australia. Mike Macrow, Craig Williams, and Alistair Scarff, ‘Credit Cards, An Ace Up the Sleeve,’ Merrill Lynch, 14 April 2000, at 5. [186]
Schwartz and Vincent. [187]
Schwartz and Vincent, Proposition 5(i) at 24.
N.B. According to correspondence from the authors, Proposition 5(ii) is incorrect as stated in the paper. The result holds only for a > 1/3.
[188]Schwartz and Vincent, Proposition 6(iii) at 27. [189]
Schwartz and Vincent at 36. [190]
Regulating Interchange Fees. [191]
Regulating Interchange Fees at 9. [192]
The force of this assumption is that bb + bm < cI + cA. If this condition were not satisfied, it would be efficient for a consumer use a card for all transactions conditional on holding a card–card use could never be excessive. The assumption made in the text allows for the possibility of both excessive and insufficient card use. [193]
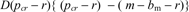
Regulating Interchange Fees, Proposition 1 at 7. [195]
Recall from the discussion of Section III.B above that this model likely overstates the economywide benefits of card holding. [196]
With a large number of competing merchants, there could be a free-rider problem with respect to promoting cardholding, but competition would lead to lower prices anyway. [197]
The key (and realistic) assumption is that the merchant cannot engage in perfect price discrimination, so that consumers enjoy positive surplus from their purchases. [198]
Schmalensee. [199]
Professors Gans and King also assert that there is an algebraic error in Schmalensee's derivation of the privately optimal interchange fee in the ‘symmetric demands case.’ (Regulating Interchange Fees at footnote 5.) [200]
Rochet and Tirole at 17. This formula assumes that merchants accept cards at the resulting merchant service fees. [201]