RBA Annual Conference – 2012 Property Market Cycles as Paths to Financial Distress Luci Ellis, Mariano Kulish and Stephanie Wallace
1. Introduction
Property market busts are usually implicated in some way in episodes of financial instability. The losses on US mortgages that sparked the recent financial crisis are a good example of this connection, as are the episodes in Japan, Scandinavia and Australia in the early 1990s, which largely stemmed from commercial property lending. One might think property loans should be fairly safe, given the protection afforded to the lender by the collateral. History suggests, though, that property market cycles cause financial and economic busts far more frequently than does unsecured lending.
Property-related loans also seem more prone to engendering banking and financial crises than loans secured against, for example, motor vehicles or business plant and equipment. Like financial securities, but unlike those other types of physical collateral, property may hold or even increase its value after the loan is extended. This fact may induce both borrowers and lenders to treat the collateral as the primary guarantee of repayment, rather than as a second line of defence should the borrower's cash flow prove insufficient to service the loan. In addition, the knowledge that property values can rise, and especially an expectation that they will, encourages lenders to permit greater leverage on property loans. As Fostel and Geanakoplos (2008) and Geanakoplos (2009) show, not only do leverage cycles induce asset price cycles, but (expected) asset price cycles induce leverage cycles too.
In this paper, we examine how the flexibility of supply and the contract features of loans influence property boom-bust cycles and the resultant financial distress. On the first of these, many authors have observed that price booms tend to be larger in markets where the supply of property is constrained, as seems to be the case in the United Kingdom, for example. It seems an obvious point that the steeper the supply curve in the property market, the more property prices will increase after some positive demand shock. In this paper we show, however, that this need not imply that the subsequent decline in prices will also be more damaging for financial stability. The price cycle by itself can be a misleading statistic of risks to financial stability, partly because debt dynamics result from a combination of both price and quantity dynamics, and partly because the distribution of debt is far more important in creating financial distress than is its aggregate value. We show that when property supply is more flexible, the distribution of debt at the end of a boom is more likely to trigger episodes of financial distress and instability.
The differing experiences of housing markets in US cities during the recent boom-bust cycle are a case in point. Housing supply in Atlanta, for example, is known to be quite flexible. As Figure 1 shows, Atlanta experienced only a small run-up in prices during the boom compared with other cities. However, the price bust has been large: using Case-Shiller data up to early 2012, housing prices in Atlanta were 36 per cent below their peak, a slightly larger fall than the 20-city composite index, and only a few percentage points less than the 40 per cent decline in Los Angeles. Importantly, prices in Atlanta are below their 2000 levels, implying that some home owners who purchased more than a decade ago are now holding a property worth less than they paid for it.
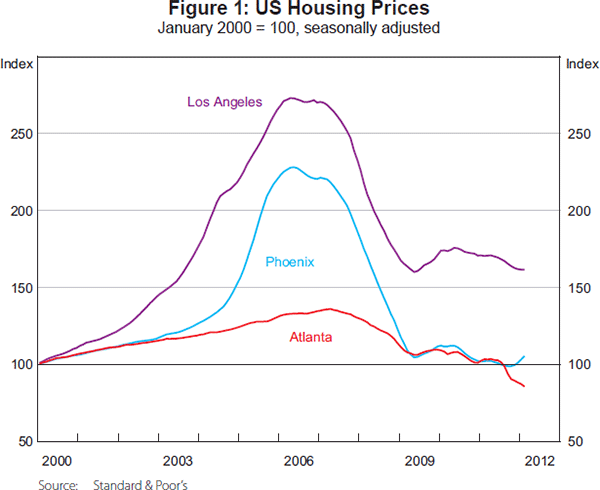
Whether a fall in prices translates into financial distress depends on a range of factors. The latest available Federal Reserve Bank of New York data (for late 2010) suggest that the fall in Atlanta has indeed resulted in high rates of negative equity, and thus arrears and foreclosures: on average, Georgia counties in the Atlanta region had arrears rates 2 percentage points above the national average of 5.3 per cent.[1] At 21.8 per cent, the 90-day arrears rate on subprime loans in Georgia, using available state-level data, was at a level similar to those in states most associated with the bubble (California, Nevada and Arizona), and noticeably above the national average (17.9 per cent), while for prime mortgages, the arrears rate in Georgia (3.4 per cent) was actually above that in Florida (3.2 per cent) and Arizona (2.9 per cent).
For a given decline in prices, whether borrowers end up in negative equity depends on their initial loan-to-value (LTV) ratios and how quickly they amortise their debt. Features of the loan contract are therefore central in translating an observed macro-level aggregate outcome to a financial stability outcome. Negative equity does not always trigger default, however. Before default occurs, there usually needs to be a problem with capacity to repay, as well as a negative equity position (Foote, Gerardi and Willen 2008). Problems might result from negative income shocks such as unemployment, but other loan contract features, such as a requirement to increase repayments or refinance altogether, can also be important.
The sources of banking crises and other episodes of financial instability are not confined to home mortgage loans. In fact, they are more often driven by losses on commercial property loans, especially on loans to developers of either residential or non-residential property. We show that cycles in commercial property can lead to episodes of financial distress that are several times worse than those spurred by cycles in housing markets.
Differences in time-to-build lags and loan contracts help explain why commercial property lending can pose more of an issue for financial stability than does mortgage lending in most countries. Time to build is usually longer for commercial property than for at least some kinds of housing, which amplifies the price cycle. In addition, the loan contract features typical in the commercial property market are more likely to encourage default. Interest-only loans are common. Because the principal is not run down over the loan term, the share of borrowers with loans worth more than the property (negative equity) is higher for any given decline in prices. Typical loan terms are also usually shorter than home mortgage loan terms in many countries, requiring borrowers to refinance periodically. If these borrowers are in negative equity at the refinancing date, they are very likely to default. Default rates are therefore likely to be higher and more concentrated than for portfolios of amortising home mortgages.
In this paper we set up a simple stock-flow dynamic partial equilibrium model of the property market and use it to simulate cycles. We illustrate how features of the property market, including supply flexibility, time to build and the prevailing loan contract features, can affect price and debt dynamics. Our key innovation is to translate those simulated cycles into measures of financial distress; we do so with an overlapping generations type structure for debt as follows: in every period we assume that a new cohort enters the market and purchases, at the current price, the net new supply of property, financed by debt subject to an LTV ratio. Given the form of the loan contract, that is, the interest rate, the term and the type of amortisation, we keep track of the distributions of debt and equity in property over time.
We show that a more responsive supply of property to prices can generate dynamics which are more likely to generate financial distress. If the flow of new property supply is highly responsive, the price response will be smaller in a boom than if supply were inflexible (Paciorek 2012). This may suggest that the downswing might be less likely to create financial distress, but we show that this is not always the case. If supply is quite responsive, large amounts of new property will be constructed during the boom, creating an overhang of excess supply once the boom ends. Prices will then fall further, potentially putting even those who bought prior to the boom into negative equity. In addition, more of the loan book will be accounted for by borrowers who bought at or near the price peak – because of the increased flow of new property purchases in those periods. Therefore if supply is more responsive, more of the loan book is liable to be in negative equity, a necessary condition of default. The effect of a highly responsive supply on loan performance is exacerbated when there are time-to-build lags, that is, if production is highly responsive to changes in price but adds to supply periods later.
In this respect, our results provide an explanation of Atlanta's experience and, more generally, the cross-country experience of recent years. The modelling exercise, however, provides a number of other insights as well. In particular, we find that the characteristics of the loan contract can be decisive in determining whether a given cycle in property prices and construction turns into an episode of financial distress and instability. We find, as in Ellis (2008), that amortisation is a pivotal determinant of the extent of negative equity.
We also find that the response of interest rates to the price cycle has an asymmetric effect on our measures of financial distress. Specifically, higher interest rates help attenuate the boom in prices but also make running down existing (variable-rate) debt more difficult and so increase the vulnerability of indebted cohorts. On the other hand, lower interest rates during the bust support property prices and simultaneously allow indebted cohorts to deleverage faster. Lower interest rates help reduce measures of financial distress through both of these channels.
These findings imply several things about the appropriate policy response. First, it would be a mistake to focus overly on housing lending at the expense of property development lending when assessing risks to financial stability. Second, policies intended to mitigate these risks should not be calibrated solely on aggregate macro-level variables such as asset price indices and credit. Diligent prudential supervision is clearly helpful, but it seems less clear from our results that tightening prescribed prudential ratios beyond some threshold can eliminate most of the increase in financial distress. And finally, while tightening monetary policy during a property boom may be helpful, it seems that it could be even more important to leave room to ease monetary policy during the bust.
The rest of this paper is structured as follows. The next section discusses our model. Section 3 presents the key results, both for a benchmark case which is calibrated to the housing market, and for another case designed to proxy for the commercial property market. Section 4 discusses some possible policy responses and Section 5 concludes.
2. Model
We present a model that captures some essential features of property markets, like the durable (stock) supply and long holding periods. It is a linear, dynamic, partial equilibrium stock-flow model of property with adaptive price expectations. Many of these assumptions, if not all, are worth relaxing in further research. But we intentionally keep the model simple, in order to focus on the channels through which property market developments can affect the degree of financial distress and thus the risks to financial stability.
Our modelling exercise can be thought of in two steps. In the first step, we use this model to generate property cycles. In the second step, we use these implied dynamics to study their financial stability implications. In particular, we assume that, in every period at the prevailing property prices and quantities generated from the first step, agents take on debt to finance the purchase of the new stock of property, subject to an LTV ratio. Given the term of the loan and interest rate, we keep track of each cohort's balance sheet using standard amortisation formulas, to explore the distribution of indebtedness, equity in their property and financial vulnerability.
2.1 First step: a simple dynamic model
We assume that the aggregate demand for property at time t, Ht, is given by the equation below.

In Equation (1), yt is (exogenous) income, which we assume to be constant
and normalise to unity; pt is the price of housing and rt
is the (exogenous) interest rate in period t; all parameters (denoted by Greek
letters) are positive. The exogenous process λt is a demand
shifter term that increases demand relative to income. There are several ways
to interpret this variable, but we treat it as representing credit conditions
relating to serviceability: if households are permitted to borrow more on the
same income, their demand for housing rises. The expected property price in
the next period is denoted as 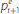 which, in turn, is updated as shown in Equation (2). Adaptive
expectations imply that any interest rate changes are
unanticipated.[2]
which, in turn, is updated as shown in Equation (2). Adaptive
expectations imply that any interest rate changes are
unanticipated.[2]

Equation (1) represents the aggregation of the behaviour of explicitly heterogeneous households (the cohorts described below). As such it cannot be directly related to the kinds of behavioural relationships that hold at the individual or representative agent level, for example the user cost equation frequently seen in the literature (e.g. Meen 1990, 2000). In addition, our model ignores taxes and has no rental market, so some of the inputs in the arbitrage relations underlying user cost are omitted. We do, however, incorporate the remaining explanatory variables from the user cost model, including housing prices, expected housing prices, income and interest rates.
The flow supply of housing, ht, is given by the expression below.

Supply responds positively to prices and negatively to interest rates, consistent with standard models in the literature, such as Topel and Rosen (1988). Period t flow supply adds to the stock in period t + J, where J corresponds to time to build. In particular, the stock of property obeys the law of motion shown in Equation (4), where J ≥ 0 and δ denotes depreciation.

Given initial conditions and time paths for λt and rt, Equations (1)–(4) determine
the path of the endogenous variables, 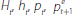 . We generate a cycle through an exogenous temporary increase
in λt, which we interpret as a temporary easing of lending
standards around
serviceability.[3]
Allowing an easing in lending standards to stimulate property demand (α1
> 0), is consistent with an assumption that buyers are credit constrained
(La Cava and Simon 2003); lending standards, or
more generally credit conditions, have previously been found to be important
drivers of household consumption and housing-related outcomes (Muellbauer and Williams 2011).
. We generate a cycle through an exogenous temporary increase
in λt, which we interpret as a temporary easing of lending
standards around
serviceability.[3]
Allowing an easing in lending standards to stimulate property demand (α1
> 0), is consistent with an assumption that buyers are credit constrained
(La Cava and Simon 2003); lending standards, or
more generally credit conditions, have previously been found to be important
drivers of household consumption and housing-related outcomes (Muellbauer and Williams 2011).
2.2 Second step: financial distress indicators
In order to translate market dynamics into measures of financial distress, like the percentage of the loan book in negative equity, or the equity shortfall of these loans as a percentage of aggregate debt, we assume an overlapping-generations structure of property buyers and track each cohort's repayment, equity and outstanding debt over time.
We interpret each period's net purchases of newly built property as being the purchases of a new cohort of households; there are N cohorts in total at any one time. To fund their purchases, the new cohort borrows at the exogenous interest rate rt. For simplicity, we abstract from any requirement to accumulate a down payment prior to purchase. This assumption ensures that households purchase their home in the period they are ‘born’, rather than delaying until they have accumulated some savings. We therefore do not have to model the housing tenure decision or a rental market; these would make useful extensions for further research.[4]
The quantity of property held by the cohort that is k years old at the start of period t is qk,t.
The cohort of buyers that enters at time t purchases the quantity
of property released by the departing cohort, qN − 1, t − 1,
and any net addition to the stock of property ht − J – δHt − 1.
Implicitly then, one can think of cohorts as repairing or maintaining their
property, so that the quantity of property held remains constant over their
lives, that is qk,t = qk+1,t+1.
The new cohort absorbs any new construction that does not offset depreciation,
so in every period the aggregate property stock equals the holdings of the
population, 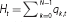 . So the quantity of property purchased by time-t
buyers, q0,t is given by Equation (5).
. So the quantity of property purchased by time-t
buyers, q0,t is given by Equation (5).

Time-t buyers take out a mortgage for κptq0,t to fund their purchase, where κ is the LTV ratio. Repayments are calculated according to Equation (6), known as the credit-foncier formula, which implies that borrowers make constant repayments over the life of the loan.[5] The proportion of the repayment going towards amortising the loan principal therefore rises over the life of the loan. This is the standard model for required loan repayments in most industrialised economies. The term of the loan T is always assumed to be less than the cohort's lifespan N. If interest rates were to remain constant over time (rt = r) – an assumption that we relax below – the constant repayment for a household that is k years old at the start of period t is given by the credit-foncier formula:

The end-of-period outstanding debt for the cohort who is k years old at the beginning of time t, if the interest rate remains constant over time, is:

If the interest rate changes, however, Equations (6) and (7) need to be recomputed with the updated values of the remaining term (T − k), interest rate and outstanding principal. The equity of each cohort is defined as the difference between the current value of the property and the debt outstanding, that is:

A commonly used measure of financial vulnerability is the share of the loan book
in negative equity. We calculate this share at each time t, St, as the debt owed by cohorts in negative equity,
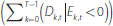 , divided by total debt outstanding:
, divided by total debt outstanding:

Interest-only loans, which are a common form of finance in commercial property markets, simply have a constant repayment equal to the interest on the initial loan value. The principal is not reduced over the term of the loan, but is instead cancelled in a lump-sum payment at maturity.
Finally, the entering cohorts are the only buyers, and the properties of the exiting cohorts are the only ones that change hands.
2.3 Calibration
For the numerical analysis we select the benchmark parameterisation shown in Table
1. Given the value of rt, the model forms a vector autoregression on the endogenous
variables, 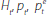 and ht. In steady state, price expectations
are equal to actual prices; that is, there are no forecast errors. We set the
interest rate rt to 3 per cent
and interpret it as a real rate. The depreciation rate of the housing stock,
δ, is chosen so that in steady state the flow supply of housing
equals 2 per cent of the stock. Income, yt, is normalised
to 1 and the measure of lending standards, λt, is
also taken to be 1 in normal times and 1.5 when lending standards ease. This
can be interpreted as an easing in a serviceability requirement that allows
borrowers to borrow 50 per cent more on the same income; for example, a repayment-to-income
ratio limit that rose from 30 per cent to 45 per cent.
and ht. In steady state, price expectations
are equal to actual prices; that is, there are no forecast errors. We set the
interest rate rt to 3 per cent
and interpret it as a real rate. The depreciation rate of the housing stock,
δ, is chosen so that in steady state the flow supply of housing
equals 2 per cent of the stock. Income, yt, is normalised
to 1 and the measure of lending standards, λt, is
also taken to be 1 in normal times and 1.5 when lending standards ease. This
can be interpreted as an easing in a serviceability requirement that allows
borrowers to borrow 50 per cent more on the same income; for example, a repayment-to-income
ratio limit that rose from 30 per cent to 45 per cent.
| Parameter | Value | |
|---|---|---|
| δ | Depreciation rate | 0.02 |
| r | Real interest rate | 0.03 |
| N | Life span (years) | 55 |
| T | Loan term (years) | 20 |
| κ | Loan-to-value ratio (per cent) | 80 |
| J | Time to build (years) | 1 |
| α0 | Constant in demand equation | 30 |
| α1 | Demand response to lending standards | 3 |
| α2 | Demand response to price expectations | 1 |
| β1 | Flow supply response to price | 0.04 |
| ω | Expectations adjustment | 0.8 |
| η | Demand response to interest rates | 35.98 |
| τ | Flow supply response to interest rates | 0.36 |
Interest rates influence both stock housing demand and flow housing supply. We set η and τ to match the observation that an increase in interest rates leads to a decrease in housing prices (Meen 1990). In particular, we set them so that, assuming a 20-year loan term, a 1 percentage point increase in interest rates leads to one-third of a percentage point reduction in the steady state price, which is within the range of past empirical estimates (e.g. Berger-Thomson and Ellis 2004). Given these values, we set α0 and β0 to obtain a steady-state price-to-income ratio of around 5, and the benchmark values of α1 and β1 so that the demand and flow supply elasticities in steady state equal 1; for supply, this is higher than the elasticity for the United Kingdom found in Meen (2000), but well below that for the United States in Topel and Rosen (1988), which is better approximated by the β1 value of 0.08 used in some of our comparator, non-benchmark simulations. The parameter ω is one of the key determinants of the system's dynamic stability; in particular, it governs the speed with which price expectations adjust and we set it so that it would take the system around five years to reach its new steady state after a one-period shock, if there were complete depreciation. The parameters ω, α0, β0, η and τ are kept fixed throughout the simulations; our conclusions do not depend on particular values of these parameters.
To derive measures of financial distress we make assumptions about the characteristics of the loan contract and study the implications of varying these characteristics. In a benchmark case, we consider mortgages on residential property, and assume loan characteristics that are realistic for this market. We take the initial loan size to be 80 per cent of the dwelling price. Given a loan term, T, of 20 years, an interest rate of 3 per cent, and the formula given by Equation (6), the implied repayment is then around 30 per cent of income. We also assume that households live for N = 55 years. The household lives in the same dwelling until it dies. Mortgages are paid down following a credit-foncier amortisation schedule. Later we apply the model to commercial property and consider interest-only loans that must be refinanced at shorter horizons. Table 2 provides details of the simulations that follow.
| Figure | Contract type | J | T | β1 |
|---|---|---|---|---|
| 2 | Amortising | 1 | 20 | 0.04 and 0.08 |
| 3 | Amortising | 0 and 3 | 20 | 0.08 |
| 4 | Amortising | 0 and 3 | 20 | 0.08 |
| 5 | Amortising | Varies | 20 | Varies |
| 6 | Amortising/interest-only | 1 | Varies | 0.08 |
| 7 | Interest-only | 3 | 5 | 0.08 |
| 8 | Amortising | 1 | 20 | 0.08 |
3. Simulation Results
We consider a temporary easing in lending standards (an increase in λt) which initiates a price boom. In reality, if the easing of a constraint is sustainable, say, because artificial government restrictions on lending in a regulated sector are rescinded, part (but not all) of the initial increase in borrowing and prices will also be sustainable. If, however, the easing in lending standards were temporary then a bust is more likely. We therefore consider a case where lending standards ease temporarily in period 10, and tighten 10 years later, in period 20.
3.1 Supply flexibility and time-to-build lags
Figure 2 compares two property cycles where cohorts take out standard amortising loans. The only difference between them is in the responsiveness of flow supply. With the benchmark calibration of β1 = 0.04, the cycle in property prices, debt and equity is such that no cohort experiences negative equity. In the alternative calibration where supply is more responsive, β1 = 0.08, there is a peak in negative equity soon after lending standards tighten (and property demand falls).
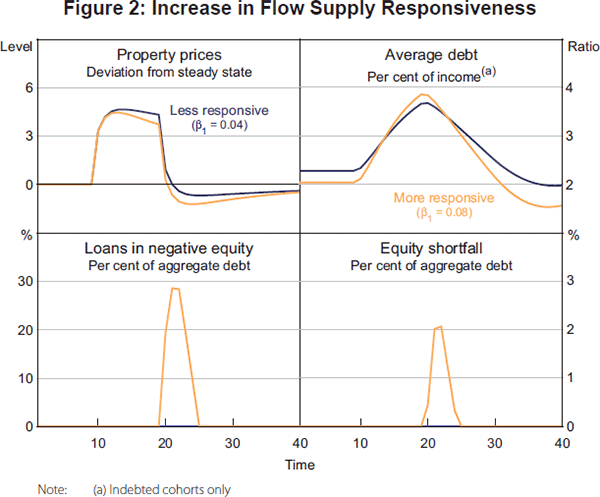
Higher flow supply responsiveness is associated with a larger peak in negative equity during the bust in spite of a lower price peak during the boom. The difference, in part, is because a larger proportion of the housing stock is held by relatively young households, who absorbed the increase in quantity during the boom and who hold relatively high levels of debt. Younger households are more vulnerable because they have had less time to amortise their debt. Additionally, and perhaps more importantly, the larger supply overhang in the more responsive case leads to a larger percentage decline in prices. It is the percentage decline that matters when considering the likelihood of outstanding debt exceeding the value of the property. This is because the LTV ratio is expressed as a proportion of the property value, and because the time taken to pay off a given proportion of a credit-foncier loan is independent of the initial loan size. Indeed, the reason why no cohorts experience negative equity when β1 = 0.04 is because the proportionate price decline is too small to drive property values below the level of debt, given the LTV ratio, interest rate and loan term.
The value of β1 governs the responsiveness of flow supply to prices. But current flow supply in the presence of time-to-build lags is predetermined. The short-run supply responsiveness is a function of both β1 and the lags implied by time to build. In particular, if time to build is short, supply responds almost immediately to current price signals. However, if there are long lags, new supply is a response to past price signals. This can be especially destabilising when construction decisions are made in response to a temporary price boom.
This case is shown in Figure 3. The lagged response of new supply exacerbates the price upswing because new supply does not put downward pressure on prices for some time. Higher prices during the boom encourage more construction, and ultimately exacerbate the price fall as new supply continues to come on line even as prices are falling.
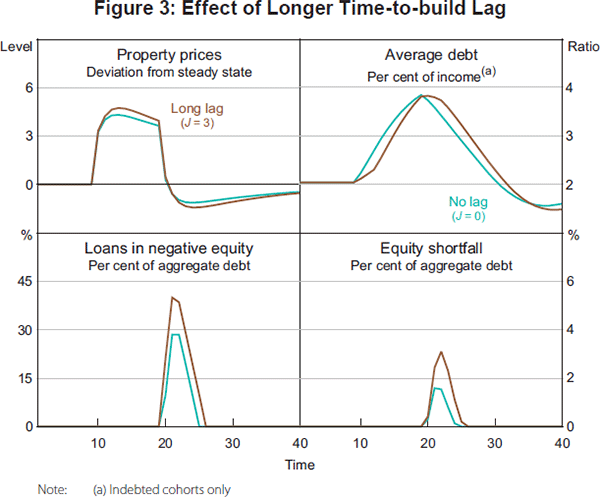
In reality, if property developers could anticipate and completely internalise the effects of their decisions to build on future prices, they might not build as much in the upswing. But in a market with many players, the developer of the marginal property project gains all of the revenue but does not bear the cost of the negative effect its project has on prices of existing properties and those already under construction.
In addition to amplifying the price cycle, time-to-build lags also increase financial distress by affecting the distribution of debt. Relatively more debt is taken on closer to the bust when new supply comes on line, as prices are higher because of the delay. Figure 4 shows, at each point in time, the percentage of total debt that was originated in the previous five years; as debt rises, the flows of new borrowing initially rise and then start to decline as a share of the (rising) total. As shown, when time-to-build lags are longer, at the time of the bust more of the debt is accounted for by younger households, who have had less time to pay down debt, and so are more likely than older households to go into negative equity.
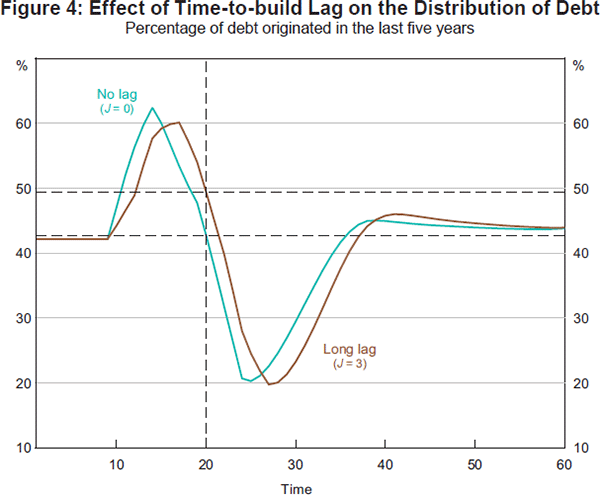
Figure 5 traces out the values of two measures of financial vulnerability – the peak-to-trough fall in prices, and the maximum equity shortfall, relative to the total loan book, over the simulation – for different values of supply flexibility (β1) and time-to-build lags (J). Time-to-build lags are most destabilising when supply is more responsive (β1 is higher). The relationship between the effects of time to build and supply responsiveness on the equity shortfall is non-linear.
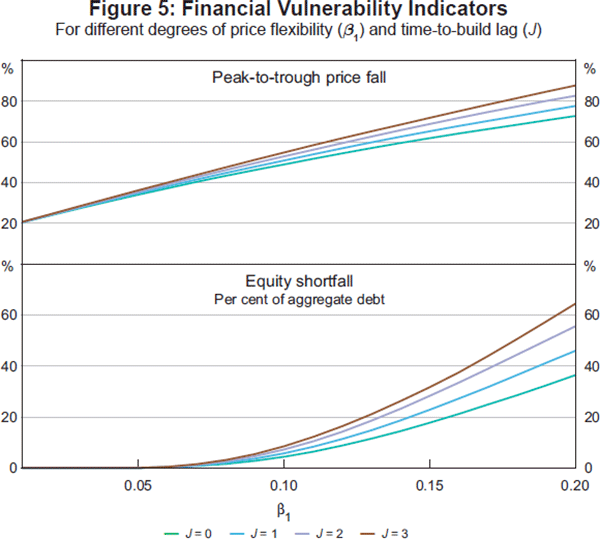
The effect of flexible property supply on measures of financial distress is consistent with the stock supply of property being large relative to the flow supply. This effect is exacerbated when there are time-to-build lags (‘hog cycles’) in construction: production is then highly responsive to changes in price but adds to supply periods later. In the meantime, prices rise even further, inducing even more supply later. The subsequent overhang of excess supply in the bust is therefore much larger, as is the decline in prices and thus the share of borrowers that potentially face negative equity. This is consistent with the findings of Chinloy (1996), that even where supply seems quite flexible, the scope for supply adjustments, rather than price changes, to absorb demand shocks is limited, making price cycles likely even in the flexible-supply case. As we have shown above, this effect is exacerbated by time-to-build lags.
3.2 Features of the loan contract
The share of the loan book that is in negative equity is sensitive to features of the loan contract. In particular, contract features which lead to principal being paid down faster reduce the incidence of negative equity. For amortising loans of a given term, of course, principal is reduced faster in the first few years under low interest rates than under high rates; this fact becomes relevant when considering possible policy responses, in Section 5.
Figure 6 shows four panels that highlight differences in measures of financial distress between amortising and interest-only loan contracts. The top left panel shows the peak share of the loan book in negative equity as a function of the LTV ratio. The top right panel shows how the peak share of the loan book in negative equity varies with the term of loan. The bottom panels translate the incidence of negative equity into a cumulative loss rate, which we describe below.
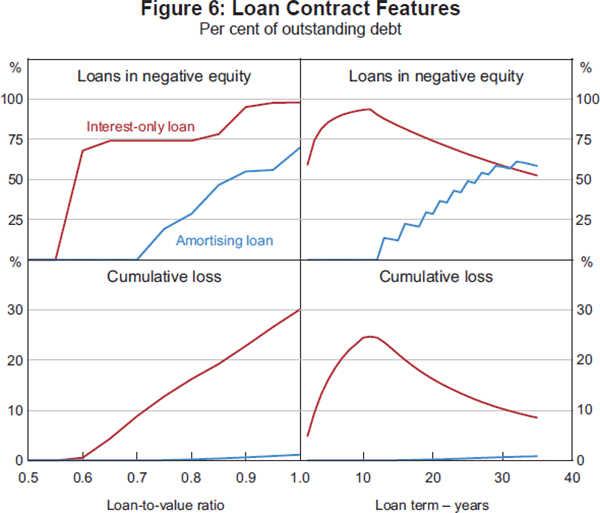
Interest-only loans are more at risk of being in negative equity because the debt is not run down over time. This can be compensated for by demanding a lower LTV ratio. Given our calibration, to ensure the losses remain below 4 per cent of aggregate debt (which seems consistent with the loss rates that sparked distress among US lenders) the LTV ratio must be set to at most 65 per cent in the interest-only case, whereas this level is never reached in the amortising case for any positive down payment (LTV ratio below 100 per cent).
The top right panel shows that, at our parameter values, the incidence of negative equity is higher at longer terms for an amortising loan. This is because two forces are at work as the term of the loan increases: outstanding debt in the economy increases as more cohorts hold onto debt for longer periods, but, as the term increases it also takes longer to run down the principal. This is particularly relevant for those cohorts who bought at boom-time prices. For a range of plausible parameter values, this second effect dominates. The stepwise shape of the amortising case reflects the inclusion of the entire debt of each additional cohort in negative equity, even though the extent of the equity shortfall is very small, and so the implied losses shown in the bottom right panel vary smoothly.
However, with interest-only loans, the amortisation effect is absent. As the term increases the outstanding debt in the economy would also increase. If the term is sufficiently short, say one period, and the LTV ratio is low enough to buffer all period-to-period price fluctuations, no cohort will ever find itself in negative equity. At longer terms, however, some price fluctuations can be sufficient to put some cohorts in negative equity. But the effect of increasing the term is bounded because at sufficiently longer terms, all cohorts who buy above the steady-state price plus the buffer given by the LTV ratio will be in negative equity at maturity. In our simulations, the price cycle depends on the number of periods of lax lending standards, the speed with which expectations adjust and the depreciation rate. At the chosen parameter values, the top right panel of Figure 6 suggests that terms of around 10 years are riskiest. But in general it is the number of periods that prices are at boom-time levels that determines – for interest-only loans and given an LTV ratio – how many cohorts will find themselves in negative equity at maturity.
Experience has shown that not all mortgage borrowers in negative equity will default; Foote et al (2008) found that, in recent decades in the United States, only about 10 per cent of borrowers in negative equity actually defaulted. Some kind of negative shock to capacity to pay is also necessary to induce a mortgage default, or even a temporary period of arrears that subsequently cures, that is, the borrower makes up the missed payments and thereby gets back on schedule (Vandell 1995; Van Order 2007; Foote et al 2008). Around 13 per cent of Australian households with mortgages experienced a period of unemployment or shift from full-time to part-time work during 2008–2009 (RBA 2011). Most of these households did not fall behind on their payments, and indeed some of them remained ahead of schedule; about half of all households with mortgages report that they are ahead of schedule. This suggests that a reasonable assumption would be that 10 per cent of households in negative equity in any period will experience an income shock that will result in default. In that case, the effects of supply responsiveness and the other factors explored above on lenders' losses will be a fraction of the total equity shortfall, which is in turn a small proportion of the loan book in negative equity.
In contrast, it is reasonable to suggest that interest-only loans will default if they are in negative equity at the point that they must be refinanced. Interest-only loans are common in commercial property markets because in property development the finance is usually repaid with the proceeds of the sale of the (completed) project. This requires, however, that property prices have not, in the meantime, fallen below the expected value on which the project plan was based. Accordingly, default depends on whether the project is in negative equity at the point that it is refinanced or completed; an income shock is not needed. Thus defaults are higher and more concentrated for interest-only loans than for amortising loans.
The distinction between amortising loans and interest-only loans helps explain why commercial real estate and property development loans have higher rates of default during busts. It also helps explain why the US subprime and other non-conforming mortgages performed so badly in the early part of the housing bust in the United States. The structure of the loan contract, namely the deeply discounted teaser rates, created large jumps in required repayments that all but forced the borrower to refinance within a few years (Gorton 2008; Ellis 2010). In effect, subprime borrowers showed high and correlated default rates, like property developers, in part because the mode of finance had come to closely resemble property development finance.
We translate the default rate into a loss rate on the assumption that the loss given default is equal to the difference between the property value and outstanding debt (the equity shortfall). The bottom panels of Figure 6 show cumulative losses, that is, the total losses over the whole simulation, expressed as a ratio to the peak level of debt. In reality, losses would probably be larger, as the recovery value of the collateral may be lower than the market price because of the effect of distress sales on realised prices. There may also be costs associated with managing the defaulted loan.
The bottom two panels of Figure 6 also show that default and loss rates are much higher under interest-only loan contracts than under amortising mortgages, even when the path of property prices is the same in both cases. The difference between loss rates in the two markets is even starker than for the peak negative equity measure, mainly because the extent of the equity shortfall is greater in the interest-only case, and because defaults are triggered by different events – refinancing rather than income shocks.
3.3 Application to commercial property
We now re-calibrate the model to capture some key features of the commercial property market (particularly property development) and its financing. These features are among those examined in Ellis and Naughtin (2010): in particular, the time to build is often longer than for housing; the loans have shorter terms and are typically non-amortising; and the loan portfolio includes a large fraction of development loans.
We explore these as possible factors that, especially in combination, could explain why commercial property lending has been more likely than housing lending to instigate a banking crisis. Historically, it is more common for bank distress to stem from losses on commercial property lending, including lending to developers of either commercial or residential property, than from mortgage lending to households. This was the pattern in the US savings and loan crisis, the episodes of banking distress in the early 1990s in Australia, Scandinavia and Japan, and the recent period in the United Kingdom, Ireland and Spain. Property developers were also disproportionately represented in the bad loans that followed the Asian financial crisis in 1997–1998. Arrears rates on housing loans can rise strongly when unemployment increases – especially if housing prices are falling – but this is an effect of the banking distress and economic downturn, not a cause. The recent US housing crash seems to have been an exception, where mortgage arrears and defaults rose sharply well before the economy turned.
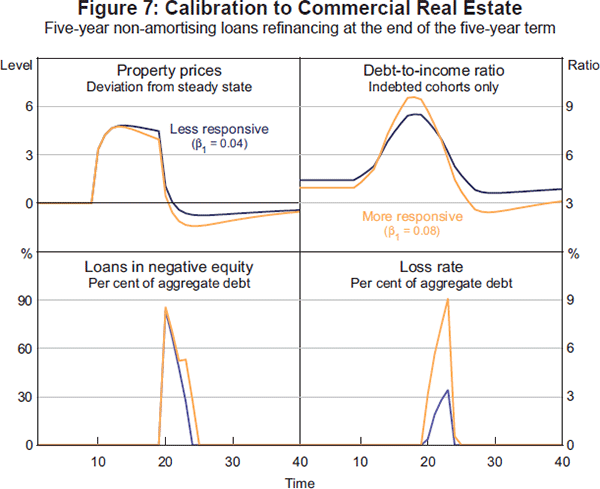
As shown before, longer times to build (J) worsen the performance of a loan portfolio during a bust; Figure 7 shows simulation paths for different levels of supply responsiveness when J = 3. The effect of longer times to build is exacerbated by the interest-only nature of property development financing. The peak shares of negative equity – at 84 per cent for the inflexible supply case and 86 per cent for the more flexible supply case – compare with figures of 0 and 29 per cent in the benchmark case shown in Figure 2, which was designed to mimic typical contract features for home mortgages. The interaction of the loan contract features with the time-to-build lags can compound their individual effects.
4. Policy Response
Previous simulations assumed a constant interest rate. Next, we consider the impact on financial stability of a counter-cyclical interest rate response. Figure 8 contains three sub-figures. Figure 8(a) compares the simulation with more flexible supply (β1 = 0.08), and in which interest rates are constant over the cycle, with the case in which interest rates are increased from 3 per cent to 5 per cent during the boom and are then lowered to 1 per cent during the bust. Figure 8(b) considers the ‘clean-only’ case where the interest rate only responds to the bust and is lowered to 1 per cent as before. Figure 8(c) considers the ‘lean-only’ case in which the interest rate increases to 5 per cent during the boom, but returns to 3 per cent, not 1 per cent, in the bust.
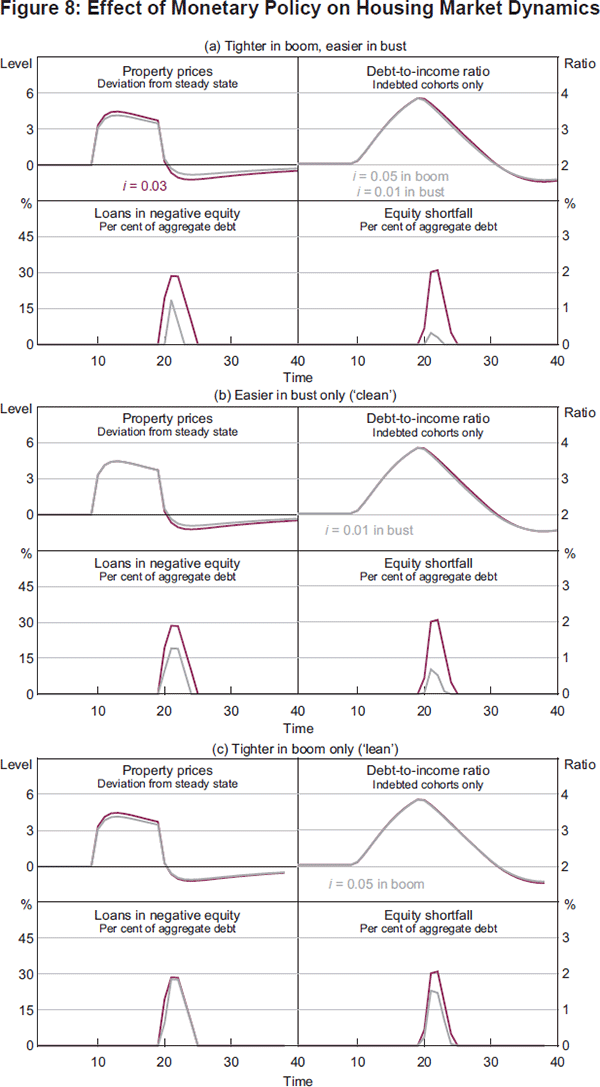
Figure 8(a) shows that a combined policy of raising rates in the boom and cutting rates in the bust reduces negative equity, by dampening demand in the boom and supporting it in the bust. There is also a second effect that loans amortise faster when interest rates are lower.[6] We have assumed default rates are a function of negative equity and any need to refinance. However, if the affordability of the repayment also affects default, cutting during the bust reduces the default rate, given negative equity, as well as the proportion of the loan book in negative equity.
Figure 8 sub-figures (b) and (c) indicate that most of the benefit of the interest rate response comes from easing during the bust, both in terms of negative equity and possible reductions in the default rate. The share of negative equity is lower because, once interest rates are lowered, amortisation occurs more quickly. This is an inherent feature of the credit-foncier loan contract and does not require borrowers to maintain their earlier repayment amounts as interest rates fall. Interestingly, the aggregate debt-to-income ratio is very similar in all four scenarios shown in Figure 8, which highlights the important point that aggregate measures mask the underlying risks to financial stability.
Another policy tool that has sometimes been advocated in the literature (e.g. Crowe et al (2011)) is a restriction on LTV ratios. This policy works through two channels as well: first, it ensures that borrowers have more equity to begin with, so there is a larger buffer to be eroded by falls in prices before the borrower is in negative equity; and second, more potential borrowers will be priced out of a rising market if they have to accumulate a larger deposit. Since we abstract from the requirement to accumulate a down payment we can only explore the first channel here. Given the findings of Wong et al (2011) that LTV caps do not prevent the boom and bust in prices, but rather protect the banking system from the effects, we suspect that this is the more relevant channel in practice.
Table 3 shows that lower initial LTV ratios do reduce the peak share of borrowers in negative equity, but they are not a panacea. If the boom-bust cycle in serviceability standards is moderate (Δλ = 0.5 to 1.0 – a 50–100 per cent expansion in borrowing capacity), bounding LTV ratios away from 100 per cent reduces peak negative equity but further restrictions make essentially no difference. If, however, the change in λ is very large, even quite severe restrictions on LTV ratios reduce – but cannot entirely forestall – a large increase in negative equity.
| Δλ | %Δp | Loan-to-value ratio | ||||
|---|---|---|---|---|---|---|
| 0.6 | 0.7 | 0.8 | 0.9 | 1.0 | ||
| 0.5 | 31 | 0.0 | 0.0 | 0.0 | 0.9 | 3.8 |
| 1.0 | 49 | 0.0 | 1.0 | 5.1 | 10.4 | 16.2 |
| 1.5 | 61 | 3.1 | 9.8 | 16.8 | 23.8 | 30.1 |
| 2.0 | 69 | 12.8 | 21.2 | 29.0 | 35.9 | 41.6 |
| 2.5 | 75 | 24.4 | 33.2 | 40.7 | 46.6 | 51.6 |
5. Conclusions and Policy Implications
In this paper we have presented a simple model that illustrates that both the flexibility of supply of new property and the terms of financing its acquisition influence how property cycles translate into financial distress, and thus impinge on financial stability. Importantly, the magnitudes of the boom and bust in prices or debt do not translate monotonically into financial distress, either for the borrowers or the lenders.
If supply is inflexible, the increase in demand manifests more as a price boom than a quantity boom, but a smaller fraction of the loan book is originated at boom-time prices. Flexible supply, on the other hand, absorbs much of the demand shock, so the price effect is smaller in the boom. In the bust phase, however, the larger supply overhang induces prices to undershoot their pre-boom level by more than if supply is fairly inflexible. This can push even cohorts who bought their property before the boom into negative equity.
More importantly, the more responsive is supply, the more property is transacted at boom prices. The fraction of the loan book liable to fall into negative equity, and perhaps default, is higher. While this finding can be partly offset by existing owners trading up, it remains true that the net addition to the stock of property must be bought by someone. Therefore the fraction of the loan book accounted for by new borrowers with higher leverage (and hence greater vulnerability to price falls) will always be greater when supply is more responsive. These effects are exacerbated by time-to-build lags, which accentuate the price cycle.
An implication of our results is that credit constraints affect the severity of the downturn and subsequent distress. If credit constraints are binding on borrowers, then an easing of those constraints will have a large effect on demand for credit, and thus for property. If the lifting of a constraint is sustainable, say because artificial government restrictions on lending in a regulated sector are rescinded, some of the initial increase in borrowing and prices will also be sustainable. If, however, the easing in lending standards is temporary – a reflection of over-exuberance or poor incentives, for example – then a severe bust becomes more likely.
A related point is that the contract terms of the loans used to finance property purchases also matter a great deal for the financial stability outcome of a given-sized property boom-bust cycle. Loans that build in some amortisation of principal over time are less destabilising, since fewer borrowers are then liable to fall into negative equity if prices fall. Short-term loans that must be rolled over are particularly dangerous: this helps explain why commercial property lending, and especially property development loans, have been so much more problematic for financial stability in the past.
Our results help explain why commercial property lending is more prone than home mortgages to busts severe enough to create a banking crisis. Longer production lags make the price cycle more severe, and the terms of the typical loan contract in this market make borrowers more likely to default. And these factors interact to exacerbate the effect of either one alone. Beyond our results, there may be several structural and institutional factors that make commercial real estate and property development lending riskier than home mortgage lending. They include the lesser attachment a firm has to its premises than a household is likely to have to its home, implying that the costs of default are lower in commercial real estate. The effect of prior defaults on current demand is also important. If a loan to an owner-occupier of commercial property defaults, the borrower may well have gone bankrupt and disappeared as a future source of demand for commercial property. In contrast, households who lose their homes to foreclosure still have to live somewhere and do not reduce demand for housing to the same extent, even if they temporarily ‘double up’ with another household as has been seen in the United States recently.
Regardless of whether we consider residential or commercial property markets, the extent of financial distress during the bust is not necessarily well proxied by the amplitude of the price cycle or by aggregate measures of indebtedness, like aggregate debt-to-income ratios. Rather, the distribution of debt, in particular the proportion of debt held by recent or more vulnerable borrowers, is a fundamental determinant of financial stability. Aggregate variables, on their own, might therefore be misleading guides for policies intended to promote financial stability. As the experience of the 2000s shows, countries with bigger price booms or the highest debt-income ratios were not necessarily the ones that had larger price busts or higher rates of mortgage defaults.
These findings raise the question of what policy options are available to forestall or ameliorate these property cycles and the distress they can engender. While it would be useful to pick a value for the responsiveness of supply that avoids building up a supply overhang, this value is almost certainly not a choice variable in the short to medium term. Recent research suggests that land availability, reflecting geographic constraints, explains much of the variation in the extent of the price upswing that can be attributed to supply factors generally (Huang and Tang 2012). Indeed, zoning laws and other land-use restrictions often seem to be a political response to manage the consequences of geographic constraints on land availability (Glaeser, Gyourko and Saiz 2008; Saiz 2010).
To the extent that policies can reduce the fixed costs of expanding supply, and thus its short-term sluggishness (time to build), they are probably worth doing. This will not eliminate property boom-bust cycles, but it may dampen their more harmful aspects. In contrast, deliberately raising the overall flexibility of supply is likely to be counterproductive if there are lags in the production process: in our model, supply delayed is worse than supply denied.
It would be ideal if some policy could perfectly offset the kinds of temporary demand shocks that can spark harmful property cycles. Certainly diligent prudential supervision can help guard against unwarranted easing in lending practices. Our findings imply that this supervision is particularly necessary in jurisdictions where supply is quite flexible. However, there are probably limits on the capacity of policy to offset this behaviour fully. Lending practices are multidimensional and hard to observe. Lenders might not even be aware that they are easing standards; although the US Senior Loan Officer Survey clearly shows the tightening subsequent to the boom, the easing during the boom is less obvious.
In addition, many demand shocks that could spark a property boom may be fundamental – stronger income or population growth, for example. It is not always clear in real time whether such a shock is permanent or temporary, and if the latter, how long it will last. Prudential supervision probably cannot be calibrated finely enough to provide a perfect counter-cyclical offset to such shocks, but it is an important part of the policy response, in that it can prevent at least some of the potential easing in lending standards that might otherwise occur.
Recently there has been considerable interest in more explicit, quantitative regulatory responses to property booms, under the label of ‘macroprudential tools’. Capping LTV ratios below 100 per cent does seem to do some good; it is no surprise that lenders typically require down payments from borrowers. But our results and the recent experience of some countries both show that further tightening of the cap does not make as much difference. If the easing in other aspects of lending standards is large enough, even a very onerous LTV cap of 60 per cent does not prevent a large subsequent increase in the prevalence of negative equity.
Interest rates, however, can be an effective counter-cyclical policy instrument. To the extent that the central bank's intellectual model of the economy incorporates the effect of property markets cycles and credit on output and thus inflation, monetary policy will offset some of the harmful effects of property cycles as a matter of course. Interestingly, our results suggest that the bulk of the effect of monetary policy on financial stability comes from easing during the bust (the ‘clean’ phase) rather than in the boom (the ‘lean’ phase). This implies that there is a case to ensure that policymakers have scope to cut interest rates when needed, which puts the constraint of the zero lower bound on interest rates in a new light.
If our results generalise further, they might have stronger implications for both the monetary policy framework and the desirable structure of property lending. Policymakers need to be aware of how the transmission of monetary policy to output and thus prices can differ depending on the structure of the mortgage market and the mode of finance for property development. If loans are predominantly variable-interest rate and monetary policy is set according to domestic circumstances, then policy easing in the face of a bust seems to be reasonably effective in reducing loan distress. On the other hand, inappropriately low interest rates during an expansion could enable a harmful boom. For example, if most loans are fixed rate or the economy is part of a slower-growing currency area, interest rates could be set too low for the segment of the property market that borrows at variable rates.
Suggesting that monetary policy respond to property cycles is not the same thing as advocating the targeting of asset prices. Our results imply that the level or change in aggregate indices of asset prices are not good guides to predicting the extent of financial distress during the bust, and neither is the amplitude of the cycle in credit.
Footnotes
See <http://data.newyorkfed.org/creditconditionsmap/>. The relevant counties are Cherokee, Clayton, Cobb, Coweta, Dekalb, Douglas, Fayette, Forsyth, Fulton, Gwinnett, Hall, Henry, Newton, Paulding and Rockdale. Flows into foreclosure were also above the national average. However, the stock of foreclosures was below those in the states most associated with the bubble, where processing backlogs have been particularly acute. [1]
An alternative specification where an arbitrary expected path of future interest rates enters into Equation (1) does not change the qualitative results presented in subsequent sections. These additional results are available from the authors on request. We chose this adaptive specification because we wanted to show that cycles can occur even without extrapolative (‘bubble’) expectations about price growth; the qualitative conclusions about supply are similar when extrapolative expectations are assumed, and for otherwise similar parameterisations, the outcomes for our financial distress metrics are, if anything, more severe. [2]
Because we have specified income as a constant, our results would be identical if we had instead manipulated α0, but this equivalence would not hold when income is rising. [3]
The down payment constraint can be binding for first home buyers (Duca and Rosenthal 1994). See, for example, Kaplan and Violante (2011) for a model in which optimising households can be thought of as saving for a down payment. [4]
If the interest rate changes, the repayment is recalculated such that it would remain constant for the rest of the loan term assuming no further rate changes. In the model all loans have variable rates. [5]
The dampening effect of interest rates on prices yields similar reductions in financial vulnerability in both the contractionary and easing phases. The amortisation effect is also of a similar absolute magnitude in both phases, although in the contractionary phase it works to offset the price effect, while easing further reduces vulnerability. In the benchmark case the price effect dominates, so raising rates in the boom reduces vulnerability. However, in alternative calibrations with a smaller price effect, raising interest rates in the boom can actually exacerbate financial vulnerability by increasing debt burdens at the time of the bust. [6]
References
Berger-Thomson L and L Ellis (2004), ‘Housing Construction Cycles and Interest Rates’, RBA Research Discussion Paper No 2004-08.
Chinloy P (1996), ‘Real Estate Cycles: Theory and Empirical Evidence’, Journal of Housing Research, 7(2), pp 173–190.
Crowe C, G Dell'Ariccia, D Igan and P Rabanal (2011), ‘How to Deal with Real Estate Booms: Lessons from Country Experiences’, IMF Working Paper No WP/11/91.
Duca JV and SS Rosenthal (1994), ‘Borrowing Constraints and Access to Owner-Occupied Housing’, Regional Science & Urban Economics, 24(3), pp 301–322.
Ellis L (2008), ‘How Many in Negative Equity? The Role of Mortgage Contract Characteristics’, BIS Quarterly Review, December, pp 81–93.
Ellis L (2010), ‘The Housing Meltdown: Why Did It Happen in the United States?’, International Real Estate Review, 13(3), pp 351–394.
Ellis L and C Naughtin (2010), ‘Commercial Property and Financial Stability – An International Perspective’, RBA Bulletin, June, pp 25–30.
Foote CL, K Gerardi and PS Willen (2008), ‘Negative Equity and Foreclosure: Theory and Evidence’, Journal of Urban Economics, 64(2), pp 234–245.
Fostel A and J Geanakoplos (2008), ‘Leverage Cycles and the Anxious Economy’, The American Economic Review, 98(4), pp 1211–1244.
Geanakoplos J (2009), ‘The Leverage Cycle’, NBER Macroeconomics Annual, 24(1), pp 1–65.
Glaeser EL, J Gyourko and A Saiz (2008), ‘Housing Supply and Housing Bubbles’, Journal of Urban Economics, 64(2), pp 198–217.
Gorton GB (2008), ‘The Panic of 2007’, in Maintaining Stability in a Changing Financial System, A Symposium sponsored by the Federal Reserve Bank of Kansas City, Kansas City, pp 131–262.
Huang H and Y Tang (2012), ‘Residential Land Use Regulation and the US Housing Price Cycle Between 2000 and 2009’, Journal of Urban Economics, 71(1), pp 93–99.
Kaplan G and GL Violante (2011), ‘A Model of the Consumption Response to Fiscal Stimulus Payments’, NBER Working Paper No 17338.
La Cava G and J Simon (2003), ‘A Tale of Two Surveys: Household Debt and Financial Constraints in Australia’, RBA Research Discussion Paper No 2003-08.
Meen GP (1990), ‘The Removal of Mortgage Market Constraints and the Implications for Econometric Modelling of UK House Prices’, Oxford Bulletin of Economics and Statistics, 52(1), pp 1–23.
Meen GP (2000), ‘Housing Cycles and Efficiency’, Scottish Journal of Political Economy, 47(2), pp 114–140.
Muellbauer J and DM Williams (2011), ‘Credit Conditions and the Real Economy: The Elephant in the Room’, Centre for Economic Policy Research Discussion Paper No 8386.
Paciorek AD (2012), ‘Supply Constraints and Housing Market Dynamics’, Board of Governors of the Federal Reserve System Finance and Economics Discussion Series No 2012-01.
RBA (Reserve Bank of Australia) (2011), ‘Box C: Household Experiences in the Downturn: Evidence from the HILDA Survey’, Financial Stability Review, March, pp 55–57.
Saiz A (2010), ‘The Geographic Determinants of Housing Supply’, The Quarterly Journal of Economics, 125(3), pp 1253–1296.
Topel R and S Rosen (1988), ‘Housing Investment in the United States’, Journal of Political Economy, 96(4), pp 718–740.
Van Order R (2007), ‘Modeling the Credit Risk of Mortgage Loans: A Primer’, University of Michigan Ross School of Business Working Paper No 1086.
Vandell KD (1995), ‘How Ruthless is Mortgage Default? A Review and Synthesis of the Evidence’, Journal of Housing Research, 6(2), pp 245–264.
Wong E, T Fong, K-F Li and H Choi (2011), ‘Loan-To-Value Ratio as a Macro-Prudential Tool – Hong Kong's Experience and Cross-Country Evidence’, Hong Kong Monetary Authority Working Paper 01/2011.