RBA Annual Conference – 2004 Inflation Measurement for Central Bankers Robert J Hill
1. Introduction
Interest in the measurement of inflation has increased significantly in recent years for a number of reasons. First, inflation rates have fallen significantly since the early 1980s. Second, many central banks have adopted inflation targets. The combination of these two factors has increased the importance of accurate measurement. Third, rapid quality improvements, particularly in the information technology and health sectors, have made accurate measurement more difficult. The final impetus was provided by the Boskin et al (1996) report which claimed that the US consumer price index (CPI) has an upward bias in excess of 1 percentage point per year, while at the same time pointing out the dramatic budgetary implications of this bias, which arises from the fact that about one-third of federal expenditure in the US is indexed to the CPI.
Most central banks that have adopted inflation targets have been very successful in getting their inflation rates down to historically low levels. It is important to remember, nevertheless, that inflation is a surprisingly slippery concept. It is not clear exactly what concept of inflation is most relevant in a central banking context, or how it can best be measured. For example, should we focus on consumer, producer and/or asset prices? Even if we agree on consumer prices, should some volatile or hard-to-measure categories such as food, energy or owner-occupied housing be excluded? Also, in a consumer context, a distinction can be drawn between a cost of goods (and services) index (COGI) and a cost of living index (COLI). Adjustments must be made for quality change and new goods and services, which the Boskin et al (1996) report identifies as the main source of bias in the US CPI. Such adjustments require econometric estimation of hedonic models. It is important to factor in estimates of possible biases when setting an inflation target, and for central banks to account for new statistical innovations introduced by national statistical offices to reduce these biases. It is not clear how frequently the index should be computed or how often it should be rebased. The increased availability of scanner data has the potential to revolutionise the construction of consumer price indices, allowing them to be computed more frequently using expenditure weights at a much finer level of aggregation than is currently possible. However, the use of scanner data may also increase the volatility of the CPI, an eventuality that might not be welcome in central banking circles.
This paper surveys these issues. My objective is not so much to provide answers as it is to alert users of inflation targets to the underlying complexities of the inflation concept itself. These issues bear directly on the choice of the inflation target and on how a central bank should respond to changes in the observed rate of inflation.
2. The Choice of Target
Most central banks target the CPI. However, it is not the only readily available measure of inflation in an economy. In particular, two notable alternatives are the producer price index (PPI) and gross domestic product (GDP) deflator. To decide which concept provides the most appropriate inflation target, it is useful to step back and consider why inflation is a problem in the first place. One significant cost of inflation is that it distorts the scarcity signals in relative price movements. This is, at least partly, attributable to the fact that, by trying to reduce menu costs, firms do not continuously adjust their prices. This leads to relative price movements with no information content that become more pronounced as the inflation rate rises. Empirically, a number of authors have demonstrated the positive correlation between the inflation rate and relative price variability (see, for example, Silver and Ioannidis 2001). This noise in relative price movements can lead to a misallocation of investment funds as well as discouraging investment by causing uncertainty. In addition, Feldstein (1997) argues that inflation reduces the after-tax real rate of interest and affects the after-tax return on some assets more strongly than others, thus further distorting investment and savings decisions. Given the emphasis in these arguments on investment, which is excluded from the domain of the CPI, this suggests that it may be better for a central bank to target the PPI or GDP deflator. However, the coverage of the PPI is quite narrow, focusing mainly on the manufacturing sector (see the International Monetary Fund's PPI manual, 2004). Hence, it is probably not a suitable target. Likewise, Kohli (1983) and Diewert (2002) note how the fact that import quantities have negative weights in the GDP deflator implies that a rise in import prices acts directly to reduce the GDP deflator. Hence, the GDP deflator is also unsuitable as an inflation target. Diewert goes on to consider a number of variants on the GDP deflator, such as deflators for C+I+G+X, C+I+G and C+G. TP Hill (1996), Woolford (1999) and Bloem, Armknecht and Zieschang (2002) advocate deflators for either C+I+G+X or C+I+G, while Diewert (1996) advocates the deflator for C+G on the grounds that prices for capital expenditure are not relevant to the deflation of current period household expenditures. He then argues that G should also be deleted due to the difficulty of obtaining meaningful prices for items of government expenditure. Hence, he concludes that the CPI is perhaps the best measure of inflation.
An additional argument in favour of the CPI as an inflation target is that it is the standard benchmark used by employees and employers in wage negotiations and is used to index public sector wages and pensions. To the extent that inflation is of the wage cost-push variety, a central bank should, therefore, target the CPI since this will directly impact inflationary expectations and hence wages. In fact, in most countries the CPI was developed as a benchmark against which public sector wages and pensions could be indexed. It was only subsequently that the CPI was adopted by central banks as an inflation target. In some countries, this has led to changes in the CPI, for example the exclusion of mortgage interest payments from the Australian CPI. One important exception from this general pattern is the European Union's Harmonised Index of Consumer Prices (HICP), which has been constructed specifically as an inflation target (for the European Central Bank). The HICP is discussed in greater detail later in the paper (also see Diewert 2002).
There has been much debate recently over whether asset prices should be included in an inflation target (see, for example, Goodhart 2001 and Tatom 2002). The current target, the CPI, includes one of the most important assets, that is, owner-occupied housing, although in Australia and New Zealand only the cost of the building materials and labour are included (this point is discussed in more detail later in the paper). It also includes consumer durables, such as cars. However, it excludes most financial assets (e.g. stocks), as do all other currently available measures of inflation. The treatment of asset prices tends to attract most attention during periods when asset and consumer price movements diverge from each other, as happened in Japan in the late 1980s and the US in the late 1990s. The concern is that when asset prices rise faster than consumer prices, this will ultimately feed back into consumer prices. It does not follow, however, that asset prices should necessarily be included in the target index. Rather, the more natural implication is that central banks should plan ahead and engage in inflation forecasting as part of their inflation-targeting strategy. Asset prices are an important input into this process.
It is sometimes argued that food and energy prices should be excluded from the inflation target. There are two main justifications for this argument. First, Blinder (1997) argues that in the US, food and energy prices are largely beyond the control of the Federal Reserve. I find this argument surprising. Even if food and energy prices are beyond the control of the Federal Reserve, it does not follow that they should be ignored. It may still be desirable to try and make adjustments elsewhere in the economy so as to keep the CPI in an acceptable range. Second, it is generally believed that the inclusion of certain food items, such as fresh fruit and vegetables, and energy items, such as petrol, makes the CPI more volatile. Cecchetti (1997) casts some doubt on this claim. Again, even if this is true, it does not follow that these very important components of consumer expenditure should be excluded from the inflation target. What it suggests is that a central bank should be allowed to take a reasonably long-term view with regard to meeting its inflation target. A central bank should not be expected to respond aggressively to every short-run fluctuation in the CPI. Clearly, there is a role for core inflation measures to help determine the direction of the underlying inflation rate by separating transitory shocks from long-run trends (see Cecchetti 1997). However, this does not mean that a core inflation measure should become the target itself.
3. The COGI versus COLI Debate
Even if it is agreed that the focus of attention is consumer expenditure, this does not resolve all conceptual ambiguities. The CPI could be defined as measuring the cost of buying a particular basket of goods and services or as the cost of achieving a given level of utility. A distinction has, therefore, been drawn in the consumer price index literature between a cost of goods index (COGI) and a cost of living index (COLI).
The main issue for a COGI is the choice of reference basket. Let pt denote the price vector of period t (the base period), and pt+k the price vector of period t+k (the current period). If the base period's basket (that is, qt) is used, we obtain a Laspeyres price index. If the current period's basket is used (that is, qt+k), we obtain a Paasche price index. Let n = 1,…, N index the goods and services included in the reference basket. It is assumed here that the goods and services under consideration do not change between periods t and t+k. The treatment of new goods and quality change are discussed later in the paper. The price of good n in period t is denoted by pt,n while the quantity of good n in the reference basket of period t is denoted by qt,n. The Laspeyres and Paasche indices are defined as follows:
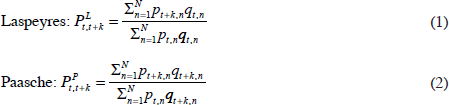
The problem with both of these indices is that they suffer from representativity bias (see TP Hill 1998). That is, to correctly measure the change in the price level, the reference basket should be representative of the two periods being compared. This problem can be dealt with by using a reference basket that is an average of the baskets of the two periods being compared. Two such indices have received attention in the price index literature.
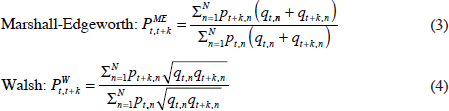
Alternatively, instead of constructing an average basket, we could take an average of Laspeyres and Paasche indices. This is the approach followed by the Fisher index, which is a geometric mean of Laspeyres and Paasche indices.

A price index can also be constructed by taking a geometric mean of price ratios. The geometric Laspeyres index weights each price ratio by its expenditure share in the base period, while the geometric Paasche index weights each price ratio by its expenditure share in the current period. By taking a geometric mean of geometric Laspeyres and geometric Paasche indices we obtain the Törnqvist index.
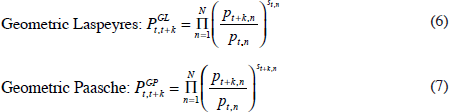
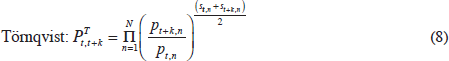
The term st,n denotes the expenditure share of good n in period t:

To avoid representativity bias, one out of the Marshall-Edgeworth, Walsh, Fisher and Törnqvist indices should be used. These indices will tend to approximate each other quite closely, so the choice between them is of limited practical significance. If required, the axiomatic approach to index numbers can be used to discriminate between them. Usually the formula that emerges as best from an axiomatic perspective is the Fisher index. In particular, it is the only one of these formulae that satisfies the factor reversal test (see Balk 1995). Nevertheless, in some circles these four indices are viewed with suspicion. Von der Lippe (2001), in particular, strongly advocates the Laspeyres index on the grounds that it is easier to interpret since it has a fixed reference basket. Among academic researchers, his is a minority position.
A COLI (see Konüs 1939) takes the following form:

where e(p, u) is an expenditure function which measures the minimum expenditure required to reach the utility level u given prices p. There are three main problems with the concept of a COLI. First, it depends on the reference utility level. Second, it assumes the existence of a representative agent. Last, but not least, it is not directly observable. We will consider each of these problems in turn.
The COLI is independent of the reference utility level only if preferences are homothetic. Clearly, in practice, preferences are not homothetic. This suggests that rich and poor people face different rates of inflation. Intuitively, this is not surprising since they buy different baskets of goods and services. For example, the price of a yacht may be a matter of concern to a rich person, but it is of complete irrelevance to a poor person. People also have different tastes. Part of this difference can be attributed to age differences. For example, the price of a hip replacement matters more to a retiree than to someone in their twenties. This brings into question the assumption of a representative agent. Attempts have been made to broaden the concept of a COLI to groups (see Pollak 1981). However, it is hard to see how this concept could be implemented in practice (see Deaton 1998).
Although the COLI is not directly observable, it is bounded from below given the reference price vector pt+k by Paasche, and from above given the reference price vector pt by Laspeyres. Paasche and Laspeyres bound the COLI because they fail to take account of the fact that consumers change their consumption patterns when relative prices change, switching from goods that have become relatively more expensive to goods that have become relatively cheaper. In other words, Paasche and Laspeyres indices are both subject (in opposite directions) to substitution bias. The substitution bias of Paasche and Laspeyres indices in a COLI context is analogous to the representativity bias of Paasche and Laspeyres indices in a COGI context.
When preferences are homothetic, Paasche and Laspeyres indices provide lower and upper bounds, respectively, on the same COLI. It can be argued, therefore, that the geometric mean of Laspeyres and Paasche (that is, Fisher) should approximate reasonably closely the underlying COLI. Alternatively, under the assumption of utility maximising behaviour, once a functional form has been specified for the expenditure function, the COLI reduces to a function of observable prices and quantities. In fact, each price index formula is exact (that is, equals the COLI) for a particular expenditure function. For example, the Törnqvist index is exact for the translog expenditure function, while the Fisher index is exact for the normalised quadratic expenditure function. Diewert (1976) argued that we should prefer price index formulae that are exact for flexible expenditure functions (that is, expenditure functions that are twice continuously differentiable and can approximate an arbitrary linearly homogeneous function to the second order). He referred to price indices that satisfy this condition as superlative. Diewert went on to identify a family of superlative formulae of the following form:[1]
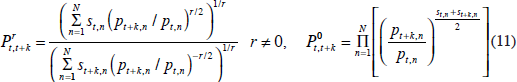
where st,n denotes the expenditure share of product n in time period t as defined in Equation (9). A second class of superlative price indices is derived implicitly as follows:

where 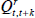 denotes the corresponding family of superlative quantity
indices defined below.
denotes the corresponding family of superlative quantity
indices defined below.
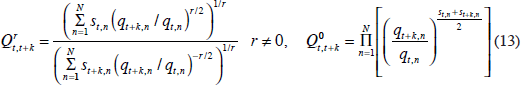
Although there are an infinite number of superlative price indices, since the parameter
r can take any finite positive or negative value, only three simplify
in an intuitively appealing manner: 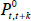 is the Törnqvist price index,
is the Törnqvist price index, 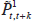 is the Walsh price index, and
is the Walsh price index, and 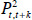 is the Fisher price index. It should be noted that
none of Laspeyres, Paasche, Marshall-Edgeworth, geometric Laspeyres and geometric
Paasche indices are superlative. It is interesting that these same three formulae
(Fisher, Walsh and Törnqvist) are the three that usually emerge as best
from an axiomatic perspective. Furthermore, for most data sets, the Fisher,
Walsh and Törnqvist indices approximate each other closely (although it
is not true that all superlative indices approximate each other closely; see
RJ Hill forthcoming). Whatever the starting point, therefore, the outcome is
similar.
is the Fisher price index. It should be noted that
none of Laspeyres, Paasche, Marshall-Edgeworth, geometric Laspeyres and geometric
Paasche indices are superlative. It is interesting that these same three formulae
(Fisher, Walsh and Törnqvist) are the three that usually emerge as best
from an axiomatic perspective. Furthermore, for most data sets, the Fisher,
Walsh and Törnqvist indices approximate each other closely (although it
is not true that all superlative indices approximate each other closely; see
RJ Hill forthcoming). Whatever the starting point, therefore, the outcome is
similar.
This seems to imply that the choice between a COGI and COLI is of merely academic interest. While this is true with regard to the choice of formula, it is not true more generally, since the COGI versus COLI stance taken by a national statistical office is a signal of intent with regard to imputations. A statistical office that favours the COLI concept is likely to quality-adjust its CPI more than a statistical office that favours the COGI concept. The stance taken in the COGI versus COLI debate may also impact on the treatment of owner-occupied housing. These issues are discussed later in the paper.
The analysis thus far ignores environmental variables that affect utility such as climate, air quality, the crime rate and the divorce rate. If these are allowed to vary when computing the COLI, this drives a wedge between the COGI and COLI concepts. This is because, by construction, a COGI does not respond to such environmental variables. At this point a distinction must be drawn between a conditional and unconditional COLI (see Pollak 1989). To illustrate this distinction, an extra term z denoting environmental variables must be added to the definition of a COLI in Equation (10). An unconditional COLI, denoted here by COLIU, allows z to vary over time.

By contrast, a conditional COLI, denoted here by COLIC, holds z fixed.

For a conditional COLI this then raises the question of whether zt or zt+k as well as ut or ut+k should be used as the reference. This decision is analogous to the one faced by a COGI with regard to the choice of reference basket (qt or qt+k). Both a COGI and a conditional COLI should only respond to movements in the quality-adjusted prices of goods and services (appropriately weighted by expenditure shares). An unconditional COLI, by contrast, will respond to changes in environmental variables even if the prices of all goods and services remain fixed. It would make no sense, therefore, for a central bank to target an unconditional COLI. For example, suppose the divorce rate rises. This, other things equal, will increase an unconditional COLI. As a result, a central bank targeting an unconditional COLI might have to respond to this by raising interest rates. Clearly, monetary policy should only respond to changes in the prices of goods and services. Furthermore, the use of an unconditional COLI would introduce a huge number of dubious imputations into the CPI (such as placing a dollar value on the change in the divorce rate).
Which concept out of a COGI and a conditional COLI provides the most appropriate inflation target for a central bank? The Statistical Office of the European Union (Eurostat) has stated clearly that the HICP is not a COLI (see Astin 1999 and Diewert 2002), as has the Australian Bureau of Statistics (ABS) with regard to the Australian CPI (see ABS 2000). In contrast, the Bureau of Labor Statistics (BLS) has adopted the COLI concept for the US CPI (see Triplett 2001). Triplett (2001) emphatically argues that the CPI should be based on the COLI concept. However, he is unduly harsh in his criticism of the COGI since he seems to equate a COGI with a Laspeyres index. This is not necessarily the case. In a COGI setting, a Laspeyres index is still subject to representativity bias. Also, the axiomatic approach can be equally well applied to the COGI concept as to the COLI concept. Nevertheless, I agree with Triplett that a central bank should not be targeting a Laspeyres index. The target should be calculated using one of the Fisher, Walsh or Törnqvist formulae. This conclusion, however, can be reached from either the COGI or constrained COLI perspective.
Even statistical offices that advocate the COLI concept are more or less forced to use a Laspeyres index due to the fact that expenditure weights for the current period are typically not available when the CPI is released. In fact, to be more precise, the index actually used typically is not even Laspeyres. This is because the expenditure weights in the CPI are drawn from one or more years, while the CPI is computed monthly or quarterly (depending on the country). The formula actually used is a Lowe index, which is defined below.

The important thing to note about a Lowe index is that the quantity vector qX does not belong to either of the periods in the comparison (see the International Labour Organization's CPI manual, 2004, Chapters 9 and 15).
The BLS has responded to the problem of not having up-to-date expenditure weights by releasing a retrospective chained Törnqvist version of the CPI one year after the ‘Laspeyres’ CPI (see Cage, Greenlees and Jackman 2003). Shapiro and Wilcox (1997) suggest an alternative approach that makes use of the Lloyd (1975)-Moulton (1996) price index, defined below.
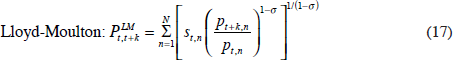
Lloyd-Moulton reduces to a Laspeyres index when σ is equal to zero. The parameter σ can be interpreted as the elasticity of substitution between pairs of commodities in the basket. The substitution bias of a Laspeyres index is a direct consequence of the fact that it sets σ equal to zero. One important feature of the Lloyd-Moulton index that it shares with the Laspeyres index is that, given a value of σ, it can be computed without the expenditure data of the current period. Shapiro and Wilcox experiment with different values of σ, and find that when set to 0.7, the Lloyd-Moulton index approximates quite closely a Törnqvist index for their data set. It is unrealistic, however, to assume that the elasticity of substitution does not vary across pairs of commodities. Nevertheless, short of estimating a whole demand system, the Lloyd-Moulton index provides a useful alternative to Laspeyres for computing the headline CPI.
4. Fixed-base versus Chained Price Indices
All the index number formulae considered above (including all the superlatives) are intransitive. For example, consider the following three ways of making a comparison between 2000 and 2002, using the Fisher formula:
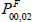 – a direct comparison
– a direct comparison
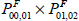 – a chained comparison through 2001
– a chained comparison through 2001
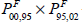 – a chained comparison through 1995
– a chained comparison through 1995
The fact that bilateral price indices are intransitive implies that each price index chain is path-dependent, and hence will generate a different answer. This has important implications for the measurement of inflation. It implies that the resulting price index series will depend both on the choice of index formula and on the way the time periods are linked together. To avoid internal inconsistencies, there should be one, and only one, path between each pair of time periods. This means that the time periods, when linked together, should form a spanning tree (see RJ Hill 2001). Three examples of spanning trees are shown in Figure 1. Each vertex in a spanning tree here denotes one of the time periods in the comparison. Each edge denotes a bilateral comparison between a pair of time periods.
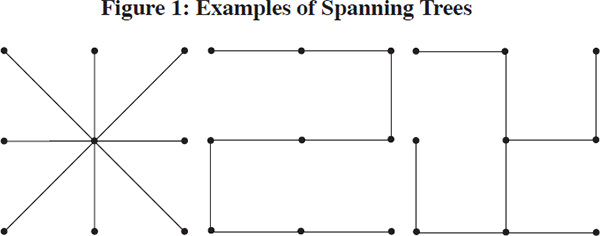
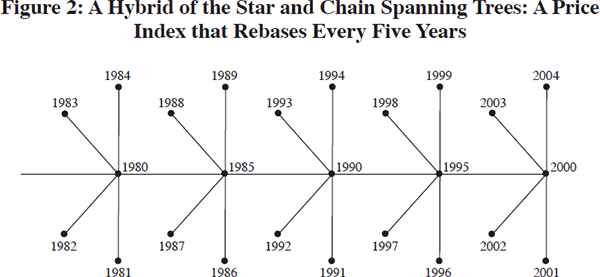
A fixed-base price index compares every period directly with the base period. This implies using a star spanning tree with the fixed base at the centre of the star (the tree on the left in Figure 1). A chained price index compares each period directly with the period chronologically preceding it. This implies using a spanning tree like the middle one in Figure 1, with the vertices ordered chronologically. Hence, it can be seen that the debate over fixed-base versus chained price indices is really a debate over the choice of spanning tree. A number of intermediate scenarios are also possible where, for example, the price index could be rebased, say, every five years. This spanning tree is depicted in Figure 2.
Something resembling a consensus has emerged in the index-number literature that price indices should be rebased every year. This tends to minimise the sensitivity of the results to the choice of price index formula. This sensitivity can be measured by the spread between Laspeyres and Paasche indices. Generally, the closer the two time periods being compared, the smaller is the substitution or representativity bias of Laspeyres and Paasche indices and hence the closer they are together. However, for quarterly non-seasonally adjusted data the case for chronological chaining is less clear cut. In this case it is not clear whether March 2002 will be more similar to June 2002 or to March 2003 (see RJ Hill 2001). Two examples of spanning trees that annually chain quarterly data are depicted in Figure 3.

Von der Lippe (2001) has criticised chaining on the grounds that it does not compare like with like. For example, a comparison between 2000 and 2003 is made by chaining together comparisons between 2000 and 2001, 2001 and 2002, and between 2002 and 2003. This means that, irrespective of the choice of formula, the comparison cannot be reduced to the pricing of a reference basket over two time periods. Von der Lippe forgets, however, that even a fixed-base comparison uses chaining, unless we are only interested in comparisons that involve the base year. Suppose, for example, that we wish to compare 2002 and 2003, when the fixed base is 1995. This implies chaining together comparisons between 2002 and 1995, and between 1995 and 2003. In general, it makes more sense if the intermediate links in the chain lie chronologically in between the two end points. This, by construction, is always true for a chronological chain, but is not true for a fixed-base price index when the two periods being compared lie on the same side of the fixed base.
5. Quality Change and New Goods
The two biggest sources of bias in the CPI identified by the Boskin et al (1996) report are new goods and quality change. New goods introduce an upward bias into the CPI (relative to a measure of the COLI) for two reasons. First, when a new good appears on the market, this in itself represents a price fall. Hicks (1940) argued that we should view the price in the period before a new good is introduced as the minimum price at which demand is zero. He referred to this price as the reservation price. Therefore, when a new good first appears, we can interpret its price as falling from the reservation price to its initial selling price. This reservation price can be estimated econometrically. For example, Hausman (1997) estimates that the reservation price of Apple Cinnamon Cheerios was about double the actual price when they first appeared on the market. Second, it typically takes a number of years for new goods to find their way into the CPI basket. This causes an upward bias since new goods tend to fall significantly in price after they are first introduced. Hausman (1999), for example, observes how mobile phones were included for the first time in the US CPI in 1998, even though they first appeared in 1983. By the end of 1997, there were 55 million mobile phones in use in the US. This second source of new goods bias in general will exceed the first, since the initial level of expenditure on new goods is typically small and hence the initial fall in price (from the reservation level) when the new good first appears should get a small weight in the CPI.
Quality change arises when a firm produces/provides a new improved version of a product/service. Frequently there is no overlap between the two versions. That is, the old version is discontinued as soon as the new version appears. Nevertheless, statistical agencies try to splice the two price series together often without making any adjustment for improved quality. Even when the old and new versions overlap the splicing process is not straightforward. Suppose, for example, that the new and old versions overlap for a single period (say period 2). Then the price index comparing periods 1 and 2 depends only on price movements in the old version, while the price index comparing periods 2 and 3 depends only on price movements in the new version. This situation can be illustrated with a simple numerical example.
Old version: p1 = 10, p2 = 9.
New version: p2 = 12, p3 = 8.
These price series can be spliced together as follows:
p1 = 10, p2 = 9, p3 = 6.
The problem is that nowhere in this approach is the superior quality of the new model captured, thus creating an upward bias in the price index (see Nordhaus 1998, p 61).
Recently there has been a huge upsurge of interest in hedonic regression methods, as a way of capturing these quality improvements (see, for example, Silver 1999, Hulten 2003, and Pakes 2003). A hedonic model regresses the price of a product on its characteristics, some of which may take the form of dummy variables. For example, consider the case of personal computers (PCs). Three characteristics that affect the quality of a PC are its speed (MH), RAM and hard drive (GB). If we have information on the price at which computer i is sold in period t (pti) and the characteristics of each computer (that is, speed, RAM and hard drive), we can then run the following regression:
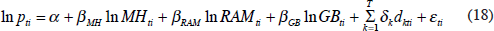
The dkti terms are dummy variables. That is dkti = 1 if t = k and dkti = 0 otherwise. Once the parameters α, βMH, βRAM, βGB, δ1…δT have been estimated, it is then possible to specify any combination of the characteristics, and obtain an estimate of the quality-adjusted price, even if no computer in that particular period had exactly this combination of characteristics. Our main focus of interest, however, is in the δK parameters since these are equal to the logarithms of the quality-adjusted price indices for each period k. There are a number of technical issues that arise in the construction of hedonic price indices, such as the weighting of different models, and the choice of characteristics and functional form (for example, semi-log versus log-log). Nevertheless, it has clearly emerged in recent years as the method of choice for quality-adjusting price indices.
The BLS started applying hedonic methods to the US CPI for the apparel category in the early 1990s. Since 1999, hedonic adjustments have also been made to computers and televisions (see Fixler et al 1999). Hedonic adjustments are now also being made for microwave ovens, refrigerators, camcorders, VCRs, DVDs, audio products, college textbooks, and washing machines (see Schultze and Mackie 2002). The BLS has probably gone further than any other statistical office in the extent of its quality adjustments. It is no coincidence that it is also one of the strongest advocates of the COLI.
There has been some debate as to whether some hedonic adjustments used by the BLS could have gone too far (see Triplett 1999, Harper 2003, and Feenstra and Knittel 2004). Harper, in particular, argues that insufficient attention may have been paid to the role of obsolescence. Returning to the example of an old and new version of a product that overlap for a single period, the price of the old version may fall in its final period on the market. Buyers will only buy at a discount since they now have a better outside option (the new version), and sellers are trying to unload their stock. To the extent that the price fall is caused by obsolescence, this means that part of the quality improvement will be captured by the spliced price index. Failure to account for this obsolescence effect could result in price indices being over-adjusted for quality change. It remains to be seen how big an issue this is in practice.
The most intractable quality-adjustment issues arise in the health sector. At present, what is measured in the CPI is the price of inputs such as a consultation with a doctor, or of a hospital stay rather than the price of outputs such as a treatment or attaining a certain health outcome. The reservation price of a health outcome that was previously unattainable may be very high, and hence a quality-adjusted medical price index could be significantly lower than the current index included in the CPI (see Cutler et al 1998).
One important implication for central banks of the more rapid introduction of new goods into the CPI and the widespread adoption of hedonic adjustment methods by national statistical offices is that it may cause an implicit change in the rate of measured inflation. The adoption of hedonic quality-adjustment methods could cause significant downward adjustments to CPI inflation. If there is no corresponding adjustment to the central bank's inflation target, this will imply a loosening of monetary policy. For this reason it is important that central banks keep abreast of statistical innovations that are introduced at their respective national statistical offices.
6. The Treatment of Owner-occupied Housing in the CPI
Owner-occupied housing is the biggest single component of the CPI in most countries. It is also one of the most contentious components. Two main approaches are in use. Australia and New Zealand use the acquisitions approach. The European Union will probably soon also adopt the acquisitions approach in its HICP (at present owner-occupied housing is excluded from the HICP). Most other countries use the rental-equivalence approach. A third approach, referred to as the user-cost approach, is used by Iceland (see Diewert 2002).
The acquisitions approach is perhaps the easiest to explain. It measures the cost of constructing new dwellings. Two features of this approach warrant further discussion. First, the focus on new dwellings is standard in a CPI context. The CPI does not attempt to track the prices of second-hand goods that are traded between households. Such transactions can be viewed as transfers between households and not a net cost incurred by the household sector. It is for this reason that sales of second-hand cars are also excluded from the domain of the CPI. Far more contentious is the fact that the acquisitions approach only measures the cost of constructing a new dwelling. That is, changes in land prices are ignored. Again, this approach can be justified on the grounds that the land is not new.
The rental-equivalence approach, by contrast, attempts to impute the rent that an owner occupier would earn if she rented out her house rather than live in it. The total value of this imputed rent across all home-owning households is then included in the CPI. In practice, these imputed rents must be estimated from data obtained from the actual rental market. This can be problematic if the rental market is thin or if the characteristics of owner-occupied and rental properties do not match (see Kurz and Hoffman 2004). To get round these problems, in the US home owners are surveyed directly and asked to estimate the rent they could receive for their homes (see Ewing, Ha and Mai 2004).
This same issue arises for all consumer durables, of which housing is just one example (although admittedly a very important one). The CPI could track the price of a new consumer durable (that is, the acquisitions approach) or the cost of the services it provides each period (that is, the rental-equivalence approach). These two approaches will give different answers. In the case of housing, the difference can be large. This is because land prices are, to some extent, implicitly included under the rental-equivalence approach. The exact interaction depends on how rents react to changes in land prices. Irrespective of the exact nature of this interaction, the total expenditure share of owner-occupied housing is larger under a rental-equivalence approach than under an acquisitions approach, and the housing price index itself is much more responsive to changes in land prices. The impact of the choice of approach on the observed expenditure share of owner-occupied housing can be observed to some extent from comparisons across countries. The US and Canada use the rental-equivalence approach. The expenditure share of owner-occupied housing in the US and Canada is about 23 per cent and 18 per cent, respectively. The corresponding expenditure shares for Australia and New Zealand (based on the acquisitions approach) are about 11 per cent and 14 per cent, respectively (see Ewing et al 2004).
The case of owner-occupied housing again illustrates two important points. First, a national statistical office's stance on the COGI versus COLI debate is a good predictor of its treatment of owner-occupied housing. Statistical offices that prefer the COGI concept tend to use the acquisitions approach, while those that prefer the COLI tend to use the rental-equivalence approach. It must be emphasised, however, that the rental-equivalence approach is in no way inconsistent with the COGI concept which, it must be remembered, tracks the prices of services as well as goods. Second, the behaviour of the CPI over time can be highly sensitive to the underlying methodologies used in its construction. These can differ from one country to the next, and can change in each country over time. For an inflation-targeting regime to function effectively, it is necessary that central banks keep abreast of these methodological issues.
7. Inflation Targeting in the European Union
The creation of the European Central Bank (ECB) necessitated the construction of a harmonised index of consumer prices (HICP) for the member countries of the European Union. This was something of a logistical nightmare given the significant differences in the methodologies used by the member countries to construct their own CPIs. The treatment of owner-occupied housing is a case in point. It ended up being put in the ‘too hard’ category and at present is completely excluded, although in the next few years it will probably be included on an acquisitions basis (see Astin 1999). Given its large share in total consumer expenditure (even on an acquisitions basis) this could cause a structural break in the HICP, particularly given that house prices are rising faster than the HICP in many EU countries.
The adoption of an inflation target for the euro area has been made more difficult by the widely differing inflation rates across the member countries. Differing inflation rates within the euro area means that monetary policy may be too stimulative in some countries and too restrictive in others. This problem could become more severe when the euro area is widened to include relatively low-price countries in Eastern Europe. This problem is probably an inevitable consequence of the creation of a single market with a common currency, since it is causing a convergence of price levels across countries (see Rogers 2001, RJ Hill 2004). That is, poorer, more labour-intensive countries (for example, Greece, Portugal and Spain) generally have lower price levels since non-tradables, in general, are more labour intensive and hence relatively cheaper (see Kravis and Lipsey 1983, and Bhagwati 1984). Increased labour and firm mobility is acting to reduce these differences, thus causing higher rates of inflation in these countries. Lower-inflation countries (such as Germany) are therefore burdened with higher interest rates than might otherwise be deemed desirable.
8. Scanner Data
It was stated earlier that ideally the CPI should be constructed using the Fisher, Törnqvist or Walsh formulae. One drawback of each of these formulae is that it requires expenditure data for the current period. At present such data are not generally available. The expenditure shares are typically obtained from household expenditure surveys, that in some countries are only undertaken at five- or even ten-year intervals. National statistical offices in most countries are more or less forced to use the Laspeyres formula, with the base year updated whenever the results of a new household expenditure survey become available. Furthermore, the expenditure data are only available at an aggregated level. For example, the Australian CPI only has expenditure data on 89 headings (see ABS 2000). Examples of these headings include milk, cheese, bread, and breakfast cereals.
This situation could change dramatically in the next few years due to the increased availability of scanner data. AC Nielson collects records of transactions at supermarkets, department stores and other shops. This has the potential to revolutionise the CPI in two ways. First, expenditure data will be available at the level of individual commodities. Second, both the price and expenditure data will be available almost continuously. Admittedly, this is only true for certain parts of the CPI, particularly food, beverages and clothing. It means, however, that at least for these components, the CPI can be computed weekly (or even daily) using a superlative formula such as Fisher. Third, scanner data can also be used in hedonic regressions to obtain more accurate estimates of quality change and better matching of characteristics and of products across geographical locations.
With these benefits also come problems. More disaggregated data tend to exhibit a stronger substitution effect. For example, a consumer is much more likely to substitute between two different brands of beer when relative prices change, than between beer and wine. A stronger substitution effect implies that the resulting price index will be more sensitive to the choice of formula. Reinsdorf (1999) and Feenstra and Shapiro (2003) document evidence of huge shifts in expenditure driven by sales on coffee and canned tuna, respectively. This is particularly troubling for chained price indices. For example, consider the case of a weekly chained Laspeyres price index for a particular supermarket. Suppose further that one brand of coffee is put on sale for one week (in week 2), and that this results in a huge increase in expenditure on this brand for the duration of the sale. The weekly chained Laspeyres index will give too little weight to the fall in the price in the coffee brand in week 2, and too much weight to its increase in price in week 3, both of which will create an upward bias. A fixed-base Laspeyres index, by contrast, will only be affected by the first of these biases and hence will have a smaller overall bias. By similar reasoning it follows that a weekly chained Paasche index could have a stronger downward bias than a fixed-base Paasche index. Although chained Fisher should be free of substitution bias, the large biases in chained Laspeyres and Paasche indices (remembering that Fisher is the geometric mean of Laspeyres and Paasche) may cause it to be somewhat erratic. Reinsdorf indeed finds evidence of erratic movements in chained Fisher indices for the case of coffee. The findings of Feenstra and Shapiro (2003) are even more surprising. For the case of canned tuna, they find that even the chained Törnqvist index has an upward bias. This is surprising since like all other superlative indices it satisfies the time-reversal test (see Balk 1995). They attribute the bias to the fact that sales are only advertised towards the end of the period, and hence there is a large spike in expenditure just before the sale ends. This means that the rise in the price of tuna when the sale ends has a much bigger effect on the index than the fall in price when the sale begins.
A number of national statistical offices have started experimenting with scanner data with the intention of eventually incorporating them into their CPIs. The experiences of Statistics Netherlands and the ABS are discussed in van Mulligen and Oei (forthcoming) and Jain and Caddy (2001), respectively. The paper by Reinsdorf (1999) is part of a broader project on the properties of scanner data at the BLS in the US.
From a central banking perspective, scanner data raise two main issues. First, there is the question of how frequently the CPI should be computed. The frequency varies across countries from monthly to quarterly. Scanner data, however, open up the possibility of computing a weekly CPI. It is not clear whether a central bank should be in favour of such a development, particularly if in the process, the CPI becomes more volatile. The increased volatility of the CPI at existing frequencies is the second issue. The use of scanner data will almost certainly increase volatility since it captures the strong substitution effects that occur at the level of individual commodities. More research is required to determine the best ways of handling scanner data. As was noted above, it is already clear that such indices should not be chained weekly. Nevertheless, it is only a matter of time until national statistical offices start using scanner data in their CPIs. Central banks, therefore, should start thinking about the implications of scanner data for inflation targeting.
9. Conclusion
Inflation targeting has been remarkably successful at bringing down inflationary expectations in most countries that have adopted it. There has been much debate regarding what rate of inflation a central bank should be targeting, and on methods for forecasting the rate of inflation so that a central bank can anticipate future trends and better meet its target. One aspect of the inflation-targeting regime, however, that has perhaps been somewhat neglected in the literature is the choice of the target price index itself. It is by no means clear that the CPI is the ideal target. The CPI in most countries was designed as a benchmark for adjusting public and private sector wages rather than as a monetary policy benchmark. Some researchers have argued that, in an inflation-targeting context, the focus of the CPI is too narrow since it ignores prices of a range of items, such as investment goods, public-sector goods and services, exports, and assets such as land and equities. In contrast, other researchers have argued that its focus is too broad, and that volatile elements such as some, or all, food and energy prices should be excluded.
Even supposing that we agree on the CPI as the inflation target, a national statistical office must still make a number of decisions that can significantly affect the index. First, there is the matter of whether the statistical office views the CPI as a COGI or COLI. This decision need not, in and of itself, necessarily have a major impact. However, in practice, it usually does, since it sets the tone with regard to the number of imputations included in the index. Two key types of imputations are made in the CPI. The first type are quality-adjustments, particularly to computers, televisions, microwave ovens, refrigerators, VCRs, DVDs, washing machines, cars and in the health sector. These adjustments are usually made using hedonic regression methods. The second type of imputation is the treatment of owner-occupied housing. Statistical offices that adopt the COLI concept tend to make more quality adjustments (potentially making the CPI lower than it would otherwise be, by as much as 1 percentage point, using the Boskin report as a rough guide), and tend to use the rental-equivalence approach for owner-occupied housing. When house prices are rising faster than the CPI excluding housing, then the use of the rental-equivalence approach will tend to make the CPI rise faster than if the acquisitions approach (generally preferred by advocates of the COGI) is used. It is important, therefore, that each central bank keeps abreast of the imputations its statistical office is including in the CPI, and in particular of any changes in methodology that might affect the index. Failure to do so could result in inadvertent changes in the stance of monetary policy. For example, if a statistical office suddenly expands its quality-adjustment program, this may require a central bank to lower its inflation target to avoid a loosening of monetary policy.
Looking forward, scanner data have the potential to revolutionise the construction of the CPI by providing far more detailed expenditure weights at far greater frequency than are currently available. The incorporation of scanner data into the CPI may make the index more volatile as well as allowing it to be computed more frequently (for example, on a weekly basis). It might be prudent for central banks also to start considering how the use of scanner data in the CPI might affect the operation of an inflation-targeting regime.
Footnote
The limit of the superlative formula as r tends to zero is the Törnqvist price index. If Equation (11) is defined for r = 0 as in the Törnqvist price index, the function is continuous on the real line. [1]
References
Astin J (1999), ‘The European Union harmonised indices of consumer prices (HICP)’, Statistical Journal of the United Nations Economic Commission for Europe, 16(2–3), pp 123–135.
Australian Bureau of Statistics (ABS) (2000), A guide to the consumer price index: 14th series, Cat No 6440.0.
Balk BM (1995), ‘Axiomatic price index theory: a survey’, International Statistical Review, 63(1), pp 69–93.
Bhagwati JN (1984), ‘Why are services cheaper in the poor countries?’, Economic Journal, 94(374), pp 279–286.
Blinder AS (1997), ‘Commentary on “Measuring short-run inflation for central bankers” by SG Cecchetti’, Federal Reserve Bank of St. Louis Review, 79(3), pp 157–160.
Bloem AM, PA Armknecht and KD Zieschang (2002), ‘Price indices for inflation targeting’, paper presented at the International Monetary Fund Seminar on the Statistical Implications of Inflation Targeting, Washington DC, February 28–March 1.
Boskin MJ, ER Dulberger, RJ Gordon, Z Griliches and D Jorgenson (1996), Toward a more accurate measure of the cost of living, Final Report to the Senate Finance Committee from the Advisory Commission to Study the Consumer Price Index, Washington DC.
Cage R, J Greenlees and P Jackman (2003), ‘Introducing the chained consumer price index’, paper presented at the Seventh Meeting of the Ottawa Group International Conference on Price Indices, Paris, 27–29 May. Available at <http://www.bls.gov/cpi/super_paris.pdf>.
Cecchetti SG (1997), ‘Measuring short-run inflation for central bankers’, Federal Reserve Bank of St. Louis Review, 79(3), pp 143–155.
Cutler D, MB McClellan, JP Newhouse and D Remler (1998), ‘Are medical prices declining? Evidence from heart attack treatments’, Quarterly Journal of Economics, 113(4), pp 991–1024.
Deaton A (1998), ‘Getting prices right: what should be done?’, Journal of Economic Perspectives, 12(1), pp 37–46.
Diewert WE (1976), ‘Exact and superlative index numbers’, Journal of Econometrics, 4, pp 114–145.
Diewert WE (1996), ‘Seasonal commodities, high inflation and index number theory’, Department of Economics, University of British Columbia Discussion Paper No 96-06.
Diewert WE (2002), ‘Harmonized indices of consumer prices: their conceptual foundations’, Swiss Journal of Economics and Statistics, 138(4), pp 547–637.
Ewing I, Y Ha and B Mai (2004), ‘What should the consumer price index measure?’, Statistics New Zealand, Consumers Price Index Revision Advisory Committee 2004 Discussion Paper.
Feenstra RC and CR Knittel (2004), ‘Re-assessing the US quality adjustment to computer prices: the role of durability and changing software’, paper presented at the CRIW Conference on Index Theory and Measurement of Prices and Productivity, Vancouver, 28–29 June.
Feenstra RC and MD Shapiro (2003), ‘High-frequency substitution and the measurement of price indices’, in RC Feenstra and MD Shapiro (eds), Scanner data and price indices, University of Chicago Press, Chicago, pp 123–146.
Feldstein M (1997), ‘The costs and benefits of going from low inflation to price stability’, in CD Romer and DH Romer (eds), Reducing inflation: motivation and strategy, University of Chicago Press, Chicago, pp 123–156.
Fixler D, C Fortuna, J Greenlees and W Lane (1999), ‘The use of hedonic regressions to handle quality change: the experience in the US CPI’, paper presented at the Fifth Meeting of the Ottawa Group International Conference on Price Indices, Reykjavik, 25–27 August.
Goodhart C (2001), ‘What weight should be given to asset prices in the measurement of inflation?’, Economic Journal, 111(472), pp F335–F356.
Harper MJ (2003), ‘Technology and the theory of vintage aggregation’, paper presented at the NBER Conference on Hard-to-measure Goods and Services in Honor of Zvi Griliches, Bethesda, Maryland, 19–20 September.
Hausman JA (1997), ‘Valuation of new goods under perfect and imperfect competition’, in TF Bresnahan and RJ Gordon (eds), The economics of new goods, University of Chicago Press, Chicago, pp 209–237.
Hausman JA (1999), ‘Cellular telephone, new products, and the CPI’, Journal of Business and Economic Statistics, 17(2), pp 188–194.
Hicks JR (1940), ‘The valuation of the social income’, Economica, 7, pp 105–124.
Hill RJ (2001), ‘Measuring inflation and growth using spanning trees’, International Economic Review, 42(1), pp 167–185.
Hill RJ (2004), ‘Constructing price indices across space and time: the case of the European Union’, American Economic Review, forthcoming.
Hill RJ (forthcoming), ‘Superlative index numbers: not all of them are super’, Journal of Econometrics.
Hill TP (1996), Inflation accounting: a manual on national accounting under conditions of high inflation, OECD, Paris.
Hill TP (1998), ‘The measurement of inflation and changes in the cost of living’, Statistical Journal of the United Nations Economic Commission for Europe, 15, pp 37–51.
Hulten CR (2003), ‘Price hedonics: a critical review’, Federal Reserve Bank of New York Economic Policy Review, 9(3), pp 5–15.
International Labour Organization (ILO) (2004), CPI manual, ILO Bureau of Statistics, Geneva. A preliminary draft of the manual is available at <http://www.ilo.org/public/english/bureau/stat/guides/cpi>.
International Monetary Fund (IMF) (2004), PPI manual, IMF, Washington DC. A preliminary draft of the manual is available at <http://www.imf.org/external/np/sta/tegppi/index.htm>.
Jain M and J Caddy (2001), ‘Using scanner data to explore unit value indices’, paper presented at the Sixth Meeting of the Ottawa Group International Conference on Price Indices, Canberra, 2–6 April.
Kohli U (1983), ‘Technology and the demand for imports’, Southern Economic Journal, 50, pp 137–150.
Konüs AA (1939), ‘The problem of the true index of the cost of living’, trans J Bronfenbrenner, Econometrica, 7, pp 10–29. Originally published in Russian in 1924.
Kravis IB and RE Lipsey (1983), ‘Toward an explanation of national price levels’, Princeton Studies in International Finance No 52.
Kurz C and J Hoffmann (2004), ‘A rental-equivalence index for owner-occupied housing in West Germany 1985 to 1998’, Deutsche Bundesbank Discussion Paper Series 1: Studies of the Economic Research Centre No 08/2004.
Lloyd PJ (1975), ‘Substitution effects and biases in nontrue price indices’, American Economic Review, 65(3), pp 301–313.
Moulton BR (1996), ‘Constant elasticity cost-of-living index in share-relative form’, Bureau of Labor Statistics, mimeo.
Nordhaus WD (1998), ‘Quality change in price indices’, Journal of Economic Perspectives, 12(1), pp 59–68.
Pakes A (2003), ‘A reconsideration of hedonic price indices with an application to PC's’, American Economic Review, 93(5), pp 1578–1596.
Pollak RA (1981), ‘The social cost-of-living index’, Journal of Public Economics, 15(3), pp 311–336.
Pollak RA (1989), The theory of the cost-of-living index, Oxford University Press, New York.
Reinsdorf MB (1999), ‘Using scanner data to construct CPI basic component indices’, Journal of Business and Economic Statistics, 17(2), pp 152–160.
Rogers JH (2001), ‘Price level convergence, relative prices, and inflation in Europe’, Board of Governors of the Federal Reserve System, International Finance Discussion Paper No 699.
Schultze C and C Mackie (eds) (2002), At what price? Conceptualizing and measuring cost-of-living and price indices, report of the Panel on Conceptual, Measurement, and Other Statistical Issues in Developing Cost-of-Living Indices, The National Academies Press, Washington DC.
Shapiro MD and DW Wilcox (1997), ‘Alternative strategies for aggregating prices in the CPI’, Federal Reserve Bank of St. Louis Review, 79(3), pp 113–125.
Silver M (1999), ‘An evaluation of the use of hedonic regressions for basic components of consumer price indices’, Review of Income and Wealth, 45(1), pp 41–56.
Silver M and C Ioannidis (2001), ‘Intercountry differences in the relationship between relative price variability and average prices’, Journal of Political Economy, 109(2), pp 355–374.
Tatom JA (2002), ‘Stock prices, inflation and monetary policy’, Business Economics, 37(4), pp 7–19.
Triplett JE (1999), ‘The Solow computer paradox: what do computers do to productivity?’, Canadian Journal of Economics, 32(2), pp 309–334.
Triplett JE (2001), ‘Should the cost-of-living index provide the conceptual framework for a consumer price index?’, Economic Journal, 111(472), pp F311–F334.
van Mulligen PH and MH Oei (forthcoming), ‘The use of scanner data in the CPI: a curse in disguise?’, Statistics Netherlands Discussion Paper.
von der Lippe PM (2001), Chain indices, a study in price index theory, Vol 16 of the Publication Series ‘Spectrum of Federal Statistics’, Statistisches Bundesamt, Wiesbaden.
Woolford K (1999), ‘Measuring inflation: a framework based on domestic final purchases’, in M Silver and D Fenwick (eds), Proceedings of the measurement of inflation conference, Cardiff Business School, Wales, pp 518–534.